第六单元 图形的相似 评估检测题(无答案)2024-2025学年九年级下册数学苏科版
文档属性
| 名称 | 第六单元 图形的相似 评估检测题(无答案)2024-2025学年九年级下册数学苏科版 |
|
|
| 格式 | docx | ||
| 文件大小 | 72.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:33:46 | ||
图片预览


文档简介
第六单元评估检测题
(时间 :70分钟 总分:100分)
一、选择题(每题 3分 ,共 30分)
1. 在下列说法中 ,正确的是( )。
A. 两个钝角三角形一定相似 B. 两个等腰三角形一定相似
C. 两个直角三角形一定相似 D. 两个等边三角形一定相似
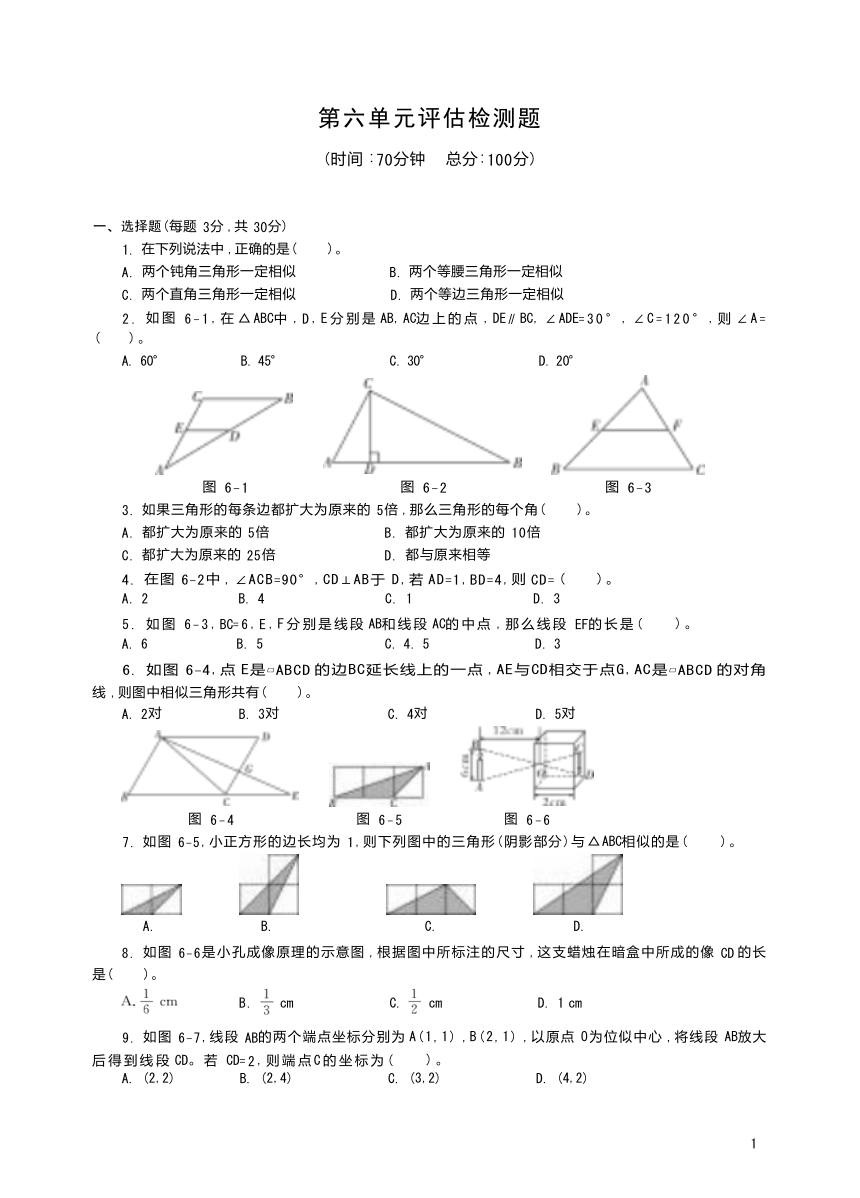
2. 如图 6-1,在 △ABC中 ,D,E分别是 AB,AC边上的点 ,DE∥BC, ∠ADE=30°, ∠C=120°,则 ∠A=
( ) 。
A. 60° B. 45° C. 30° D. 20°
图 6-1 图 6-2 图 6-3
3. 如果三角形的每条边都扩大为原来的 5倍 ,那么三角形的每个角( )。
A. 都扩大为原来的 5倍 B. 都扩大为原来的 10倍
C. 都扩大为原来的 25倍 D. 都与原来相等
4. 在图 6-2中 , ∠ACB=90°,CD⊥AB于 D,若 AD=1,BD=4,则 CD= ( )。
A. 2 B. 4 C. 1 D. 3
5. 如图 6-3,BC=6,E,F分别是线段 AB和线段 AC的中点 ,那么线段 EF的长是( )。
A. 6 B. 5 C. 4. 5 D. 3
6. 如图 6-4,点 E是 ABCD 的边BC延长线上的一点 ,AE与CD相交于点G,AC是 ABCD 的对角 线 ,则图中相似三角形共有( )。
A. 2对 B. 3对 C. 4对 D. 5对
图 6-4 图 6-5 图 6-6
7. 如图 6-5,小正方形的边长均为 1,则下列图中的三角形(阴影部分)与 △ABC相似的是( )。
A. B. C. D.
8. 如图 6-6是小孔成像原理的示意图 ,根据图中所标注的尺寸 ,这支蜡烛在暗盒中所成的像 CD 的长 是( )。
B. cm C. cm D. 1 cm
9. 如图 6-7,线段 AB的两个端点坐标分别为 A(1,1) ,B(2,1) ,以原点 O为位似中心 ,将线段 AB放大 后得到线段 CD。若 CD=2,则端点C的坐标为( )。
A. (2,2) B. (2,4) C. (3,2) D. (4,2)
1
图 6-7 图 6-8
10. 如图 6-8,梯形 ABCD 的对角线交于点 O,有以下四个结论 :
①△AOB∽△COD;②△AOD∽△ACB;
③S△DOC ∶S△AOD =DC ∶AB;④S△AOD =S△BOC 。 其中始终正确的有( )。
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每题 3分 ,共 21分)
11. 在比例尺为 1 ∶500 000的福建省地图上 ,量得省会福州到漳州的距离约为 46厘米 ,则福州到漳州 实际距离约为 千米 。
12. 若线段 a,b,c,d成比例 ,其中 a=5 cm,b=7 cm,c=4 cm,则 d= 。
13. 若 c2 =10ab,则 c是 2a与 的比例中项 。
14. 如图 6-9,已知 P是线段 AB的黄金分割点 ,且 PA>PB,若 S1 表示 PA为一边的正方形的面积 , S2 表示长是 AB,宽是 PB的矩形的面积 ,则 S1 S2。 (填“>”“= ”“< ”)
图 6-9 图 6-10
15. 如图 6-10,在 △ABC和 △EBD中 , ,△ABC与 △EBD的周长之差为 10cm,则
△ABC的周长是 。
16. 如图 6-11,△ABC中 ,AB=AC=13,BC=10,D为 BC 中点 ,DE⊥AB于 E,则DE= 。
图 6-11 图 6-12
17. 如图 6-12,已知 CO1 是 △ABC的中线 ,过点 O1 作 O1E1 ∥AC交BC于点E1 ,连接 AE1 交 CO1 于 点 O2 ;过点 O2 作 O2E2 ∥AC交 BC于点 E2 ,连接 AE2 交 CO1 于点 O3 ;过点 O3 作 O3E3 ∥AC交 BC于点 E3 , … ,依此类推 ,得到点 O4 ,O5 , … ,On 和点 E4 ,E5 , … ,En,则OnEn = AC。 (用含 n的代数式表 示)
三、解答题(共 46分)
18. (8分)如图 6-13所示 ,AD,BE是钝角 △ABC的边 BC,AC上的高 ,求证 :
图 6-13
2
19. (9分)如图 6-14,梯形 ABCD 中 ,AB∥DC, ∠B=90°,E为 BC上一点 ,且 AE⊥ED。若 BC= 12, DC=7,BE ∶EC=1 ∶2,求 AB的长 。
图 6-14
20. (10分)阳光通过窗户照到室内 ,在地面上留下 2. 7米宽的光亮区 ,如图 6-15,已知亮区一边到窗下 墙脚的距离 CE=8. 7米 ,窗口高 AB=1. 8米 ,那么窗口底边离地面的高 BC是多少米
图 6-15
21. (10分) 在 图 6- 16 的 方 格 纸 中 , △OAB 的 顶 点 坐 标 分 别 为 O(0,0)、A( - 2, -1)、B( -1, -3) , △O1A1B1 与 △OAB是关于点 P 为位似中心的位似图形 。
(1)在图中标出位似中心 P 的位置 ,并写出点 P及点 B 的对应点 B1 的坐标 ;
(2)以原点 O为位似中心 ,在位似中心的同侧画出 △OAB的一个位似 △OA2B2 ,使它与 △OAB的相似 比为 2 ∶1。并写出点 B 的对应点 B2 的坐标 ;
(3) △OAB 内部一点 M 的坐标为(a,b) ,写出M 在 △OA2B2 中的对应点 M2 的坐标 ;
(4)判断 △OA2B2 能否看作是由 △O1A1B1 经过某种变换后得到的图形 ,若是 ,请指出是怎样变换得到
的(直接写答案)。
3
22. (12分)阅读理解:在图 6-17中 ,如图(1) ,在四边形 ABCD 的边 AB上任取一点 E(点 E不与 A,B 重合) ,分别连接 ED,EC,可以把四边形 ABCD分成三个三角形 ,如果其中有两个三角形相似 ,我们就把 E 叫作四边形 ABCD的边 AB上的“相似点 ”;如果这三个三角形都相似 ,我们就把 E 叫作四边形 ABCD 的边 AB上的“强相似点 ”。解决问题 :
图(1) 图(2) 图(3)
图 6-17
(1)如图(1) , ∠A= ∠B= ∠DEC=45°,试判断点 E是否是四边形 ABCD 的边 AB上的相似点 ,并说明 理由 ;
(2)如图(2) ,在矩形 ABCD 中 ,A,B,C,D 四点均在正方形网格(网格中每个小正方形的边长为 1)的格 点(即每个小正方形的顶点)上 ,试在图(2)中画出矩形 ABCD 的边 AB上的强相似点 ;
(3)如图(3) ,将矩形 ABCD沿 CM 折叠 ,使点 D落在 AB边上的点 E 处 ,若点 E恰好是四边形 ABCD 的边 AB上的一个强相似点 ,试探究 AB与 BE 的数量关系 。
4
(时间 :70分钟 总分:100分)
一、选择题(每题 3分 ,共 30分)
1. 在下列说法中 ,正确的是( )。
A. 两个钝角三角形一定相似 B. 两个等腰三角形一定相似
C. 两个直角三角形一定相似 D. 两个等边三角形一定相似
2. 如图 6-1,在 △ABC中 ,D,E分别是 AB,AC边上的点 ,DE∥BC, ∠ADE=30°, ∠C=120°,则 ∠A=
( ) 。
A. 60° B. 45° C. 30° D. 20°
图 6-1 图 6-2 图 6-3
3. 如果三角形的每条边都扩大为原来的 5倍 ,那么三角形的每个角( )。
A. 都扩大为原来的 5倍 B. 都扩大为原来的 10倍
C. 都扩大为原来的 25倍 D. 都与原来相等
4. 在图 6-2中 , ∠ACB=90°,CD⊥AB于 D,若 AD=1,BD=4,则 CD= ( )。
A. 2 B. 4 C. 1 D. 3
5. 如图 6-3,BC=6,E,F分别是线段 AB和线段 AC的中点 ,那么线段 EF的长是( )。
A. 6 B. 5 C. 4. 5 D. 3
6. 如图 6-4,点 E是 ABCD 的边BC延长线上的一点 ,AE与CD相交于点G,AC是 ABCD 的对角 线 ,则图中相似三角形共有( )。
A. 2对 B. 3对 C. 4对 D. 5对
图 6-4 图 6-5 图 6-6
7. 如图 6-5,小正方形的边长均为 1,则下列图中的三角形(阴影部分)与 △ABC相似的是( )。
A. B. C. D.
8. 如图 6-6是小孔成像原理的示意图 ,根据图中所标注的尺寸 ,这支蜡烛在暗盒中所成的像 CD 的长 是( )。
B. cm C. cm D. 1 cm
9. 如图 6-7,线段 AB的两个端点坐标分别为 A(1,1) ,B(2,1) ,以原点 O为位似中心 ,将线段 AB放大 后得到线段 CD。若 CD=2,则端点C的坐标为( )。
A. (2,2) B. (2,4) C. (3,2) D. (4,2)
1
图 6-7 图 6-8
10. 如图 6-8,梯形 ABCD 的对角线交于点 O,有以下四个结论 :
①△AOB∽△COD;②△AOD∽△ACB;
③S△DOC ∶S△AOD =DC ∶AB;④S△AOD =S△BOC 。 其中始终正确的有( )。
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每题 3分 ,共 21分)
11. 在比例尺为 1 ∶500 000的福建省地图上 ,量得省会福州到漳州的距离约为 46厘米 ,则福州到漳州 实际距离约为 千米 。
12. 若线段 a,b,c,d成比例 ,其中 a=5 cm,b=7 cm,c=4 cm,则 d= 。
13. 若 c2 =10ab,则 c是 2a与 的比例中项 。
14. 如图 6-9,已知 P是线段 AB的黄金分割点 ,且 PA>PB,若 S1 表示 PA为一边的正方形的面积 , S2 表示长是 AB,宽是 PB的矩形的面积 ,则 S1 S2。 (填“>”“= ”“< ”)
图 6-9 图 6-10
15. 如图 6-10,在 △ABC和 △EBD中 , ,△ABC与 △EBD的周长之差为 10cm,则
△ABC的周长是 。
16. 如图 6-11,△ABC中 ,AB=AC=13,BC=10,D为 BC 中点 ,DE⊥AB于 E,则DE= 。
图 6-11 图 6-12
17. 如图 6-12,已知 CO1 是 △ABC的中线 ,过点 O1 作 O1E1 ∥AC交BC于点E1 ,连接 AE1 交 CO1 于 点 O2 ;过点 O2 作 O2E2 ∥AC交 BC于点 E2 ,连接 AE2 交 CO1 于点 O3 ;过点 O3 作 O3E3 ∥AC交 BC于点 E3 , … ,依此类推 ,得到点 O4 ,O5 , … ,On 和点 E4 ,E5 , … ,En,则OnEn = AC。 (用含 n的代数式表 示)
三、解答题(共 46分)
18. (8分)如图 6-13所示 ,AD,BE是钝角 △ABC的边 BC,AC上的高 ,求证 :
图 6-13
2
19. (9分)如图 6-14,梯形 ABCD 中 ,AB∥DC, ∠B=90°,E为 BC上一点 ,且 AE⊥ED。若 BC= 12, DC=7,BE ∶EC=1 ∶2,求 AB的长 。
图 6-14
20. (10分)阳光通过窗户照到室内 ,在地面上留下 2. 7米宽的光亮区 ,如图 6-15,已知亮区一边到窗下 墙脚的距离 CE=8. 7米 ,窗口高 AB=1. 8米 ,那么窗口底边离地面的高 BC是多少米
图 6-15
21. (10分) 在 图 6- 16 的 方 格 纸 中 , △OAB 的 顶 点 坐 标 分 别 为 O(0,0)、A( - 2, -1)、B( -1, -3) , △O1A1B1 与 △OAB是关于点 P 为位似中心的位似图形 。
(1)在图中标出位似中心 P 的位置 ,并写出点 P及点 B 的对应点 B1 的坐标 ;
(2)以原点 O为位似中心 ,在位似中心的同侧画出 △OAB的一个位似 △OA2B2 ,使它与 △OAB的相似 比为 2 ∶1。并写出点 B 的对应点 B2 的坐标 ;
(3) △OAB 内部一点 M 的坐标为(a,b) ,写出M 在 △OA2B2 中的对应点 M2 的坐标 ;
(4)判断 △OA2B2 能否看作是由 △O1A1B1 经过某种变换后得到的图形 ,若是 ,请指出是怎样变换得到
的(直接写答案)。
3
22. (12分)阅读理解:在图 6-17中 ,如图(1) ,在四边形 ABCD 的边 AB上任取一点 E(点 E不与 A,B 重合) ,分别连接 ED,EC,可以把四边形 ABCD分成三个三角形 ,如果其中有两个三角形相似 ,我们就把 E 叫作四边形 ABCD的边 AB上的“相似点 ”;如果这三个三角形都相似 ,我们就把 E 叫作四边形 ABCD 的边 AB上的“强相似点 ”。解决问题 :
图(1) 图(2) 图(3)
图 6-17
(1)如图(1) , ∠A= ∠B= ∠DEC=45°,试判断点 E是否是四边形 ABCD 的边 AB上的相似点 ,并说明 理由 ;
(2)如图(2) ,在矩形 ABCD 中 ,A,B,C,D 四点均在正方形网格(网格中每个小正方形的边长为 1)的格 点(即每个小正方形的顶点)上 ,试在图(2)中画出矩形 ABCD 的边 AB上的强相似点 ;
(3)如图(3) ,将矩形 ABCD沿 CM 折叠 ,使点 D落在 AB边上的点 E 处 ,若点 E恰好是四边形 ABCD 的边 AB上的一个强相似点 ,试探究 AB与 BE 的数量关系 。
4
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
