2024-2025学年北师大版七年级数学下册2.1 两条直线的位置关系课时2 垂直 课件(共36张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册2.1 两条直线的位置关系课时2 垂直 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览






文档简介
(共36张PPT)
北师大版七年级数学下册课件
第二章 相交线与平行线
2.1 两条直线的位置关系
课时2 垂直
1.了解垂线的有关概念、性质及画法,了解点到直
线的距离的概念;
2.能够运用垂线的有关性质进行运算,并解决实际
问题.(重点、难点)
学习目标
新课讲解
知识点1 垂线的概念
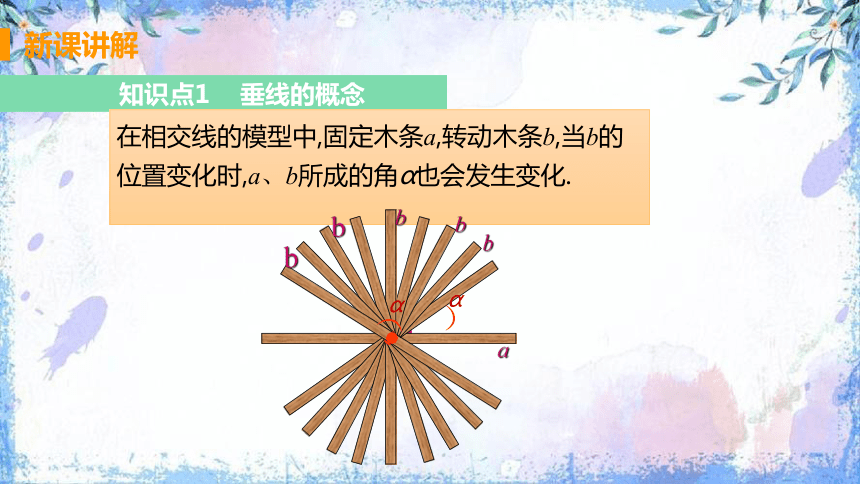
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
新课讲解
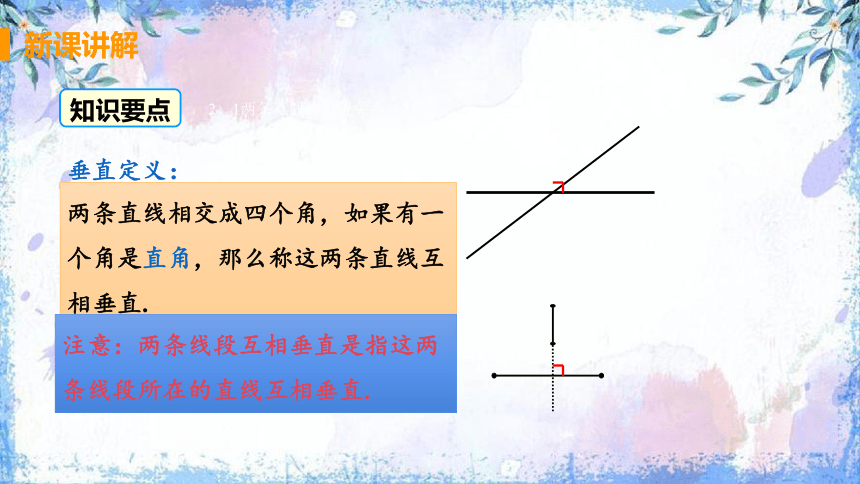
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
2、1两条直线的位置关系(2)
垂直定义:
知识要点
新课讲解
如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m ⊥ l).
把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示法
新课讲解
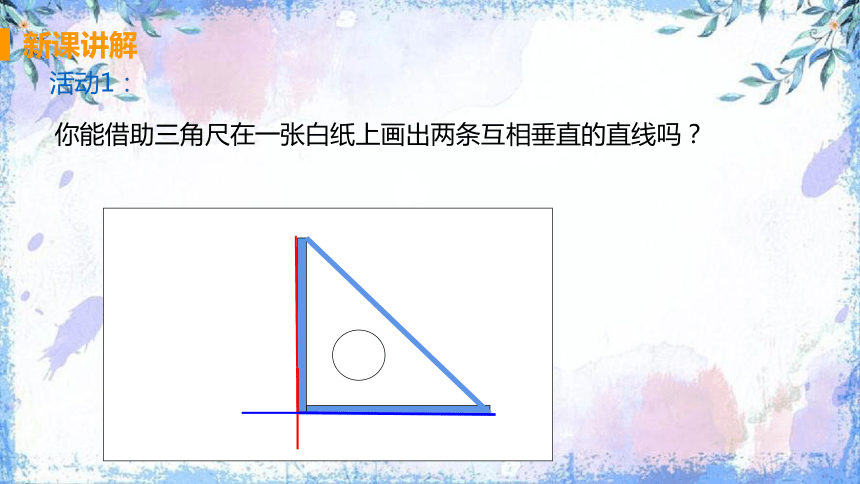
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
活动1:
新课讲解
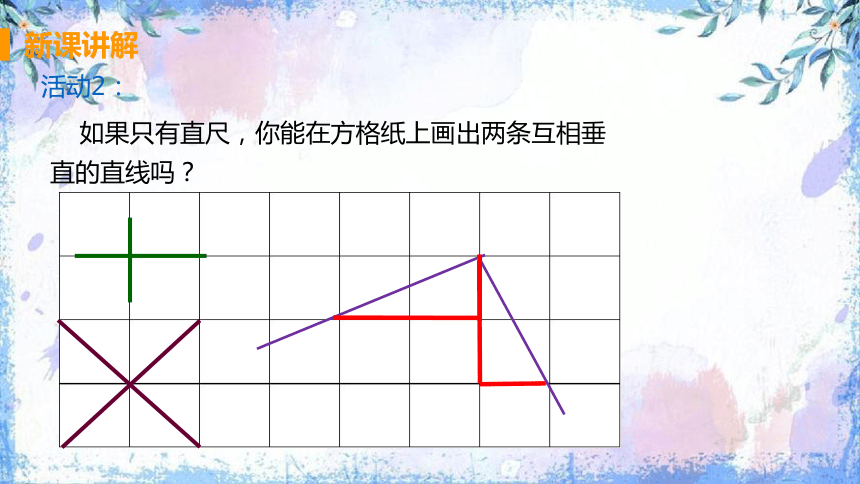
如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
活动2:
新课讲解
知识点2 垂线的画法及基本事实
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
A
.B
l
.
新课讲解
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
总结归纳
新课讲解
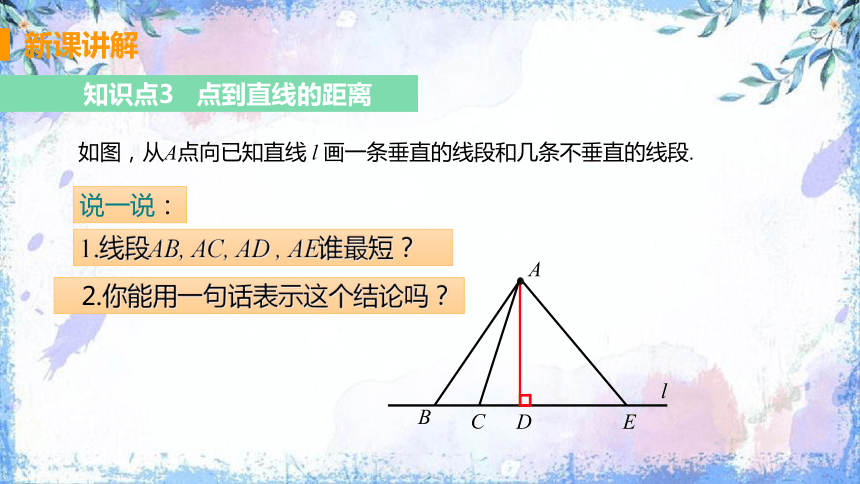
知识点3 点到直线的距离
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
新课讲解
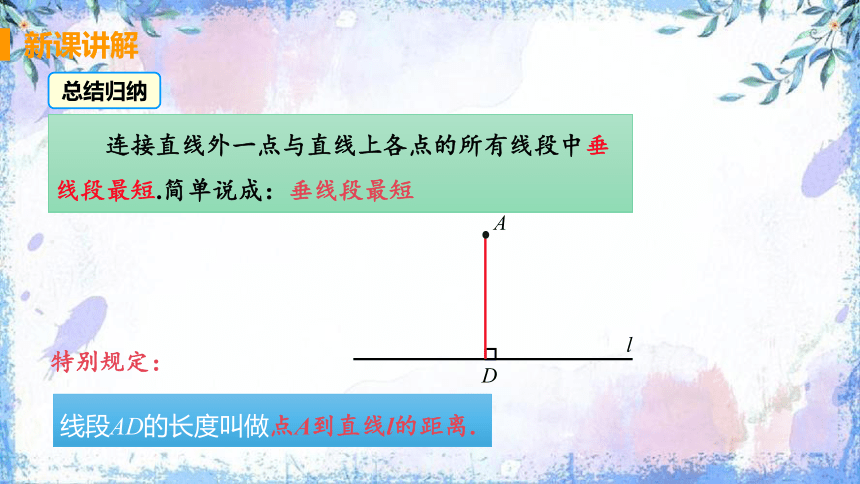
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短
线段AD的长度叫做点A到直线l的距离.
总结归纳
特别规定:
D
l
A
课堂小结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
当堂小练
.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
当堂小练
.找出图中互相垂直的线段:
AO ⊥ CO
BO ⊥DO
A
B
C
D
O
.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短
的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
知识点一:垂直的概念及表示
(1)定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相 ,其中的一条直线叫做另一条直线的垂线,它们的交点叫做 .
(2)表示方法:直线AB与直线CD垂直,记作AB CD.
⊥
垂足
垂直
1.如图,直线AB与CD相交于点O.
(1)若∠AOC= ,则AB⊥CD;
(2)若AB⊥CD,则∠AOC= .
90°
90°
知识点二:垂线的两种画法
(1)利用三角尺的两条直角边或刻度线与所在边的垂直关系画,它的基本步骤是:一靠、二过、三画,即靠已知直线→过定点→画垂线.
(2)利用量角器画,主要是画一个90°的角来得到垂线.
2.(北师7下P41、人教7下P5)如图,过点P画出射线AB或线段AB的垂线.
答案图
解:如图,直线m即为所求作.
结论:平面内,过一点 一条直线与已知直线垂直.
有且只有
知识点三:垂线段的性质
直线外一点与直线上各点连接的所有线段中,
最短.简单说成: .
如图,最短的线段是 .
PO
垂线段最短
垂线段
3.如图,PB⊥m,垂足为B,A为直线m上异于点B的点,则PB<PA的理由是 .
垂线段最短
知识点四:点到直线的距离
如图,过点A作l的垂线,垂足为B,线段 的长度叫做点A到直线l的距离.
注意:距离是一个数量概念.
AB
4.如图,OD⊥BC,垂足为 D,BD=6,OD=8,OB=10,那么点B到OD的距离为 ,点O到BC的距离为 ,
O,B两点之间的距离为 .
10
8
6
5.【例1】(北师7下P43、人教7下P5)如图,某单位要在河岸l上建一个水泵房引水到C处,做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是
.
垂线段最短
6.【例2】(人教7下P8)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
解:因为EO⊥AB,所以∠BOE=90°,
因为∠EOC=35°,所以∠BOC=∠BOE+∠EOC=125°.
所以∠AOD=∠BOC=125°.
7.【例3】如图,分别过点A,B画OA,OB的垂线.
答案图
解:如图,AD,BC即为所求作.
8.【例4】如图,O是直线AB上一点,∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,
并说出理由.
解:(1)因为∠AOC+∠BOC=180°,∠BOC=3∠AOC,
所以3∠AOC+∠AOC=180°.解得∠AOC=45°.
因为OC平分∠AOD,所以∠COD=∠AOC=45°.
(2)OD⊥AB.理由如下:由(1)知,∠AOC=∠COD=45°,
所以∠AOD=∠AOC+∠COD=90°.
所以OD⊥AB.
9.(跨学科融合)(北师7下P42、人教7下P9)如图,这是小明同学在体育课上跳远后留下的脚印,怎样测量他的成绩呢 请你画一画,其依据是 .
解:如图,测量垂线段PH的长即可.
垂线段最短
答案图
10.如图,直线AB,CD相交于点O,OM平分∠AOC,ON⊥OM,∠BOD=45°,求∠CON的度数.
解:因为∠BOD=45°,
所以∠AOC=∠BOD=45°,
因为OM平分∠AOC,
所以∠COM=∠AOC=22.5°.
因为ON⊥OM,所以∠MON=90°,
所以∠CON=∠MON-∠COM=67.5°.
11.如图,已知∠AOB和OA上一点P.
(1)过点P画PC⊥OA,交OB于点C;
(2)过点P画PD⊥OB,垂足是点D.
答案图
解:(1)(2)如图所示.
★12.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断OD,OE的位置关系,并说明理由;
(2)若∠AOD=30°,试说明OC平分∠AOE;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为 .
70°
解:(1)OD⊥OE,理由如下:
因为OD,OE分别为∠AOC,∠BOC的平分线,
所以∠COD=∠AOC,∠COE=∠BOC,
所以∠EOD=∠AOC+∠BOC=∠AOB=90°,
所以OD⊥OE.
(2)因为∠AOD=30°,所以∠COD=30°,
所以∠COE=90°-30°=60°,∠COA=60°,
所以∠COE=∠COA,所以OC平分∠AOE.
布置作业
请完成课后对应习题
感谢大家观看
北师大版七年级数学下册课件
第二章 相交线与平行线
2.1 两条直线的位置关系
课时2 垂直
1.了解垂线的有关概念、性质及画法,了解点到直
线的距离的概念;
2.能够运用垂线的有关性质进行运算,并解决实际
问题.(重点、难点)
学习目标
新课讲解
知识点1 垂线的概念
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
新课讲解
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
2、1两条直线的位置关系(2)
垂直定义:
知识要点
新课讲解
如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:l⊥m(或m ⊥ l).
把互相垂直的两条直线的交点叫作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示法
新课讲解
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
活动1:
新课讲解
如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
活动2:
新课讲解
知识点2 垂线的画法及基本事实
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
A
.B
l
.
新课讲解
垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
总结归纳
新课讲解
知识点3 点到直线的距离
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
新课讲解
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短
线段AD的长度叫做点A到直线l的距离.
总结归纳
特别规定:
D
l
A
课堂小结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
当堂小练
.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
当堂小练
.找出图中互相垂直的线段:
AO ⊥ CO
BO ⊥DO
A
B
C
D
O
.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短
的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
知识点一:垂直的概念及表示
(1)定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相 ,其中的一条直线叫做另一条直线的垂线,它们的交点叫做 .
(2)表示方法:直线AB与直线CD垂直,记作AB CD.
⊥
垂足
垂直
1.如图,直线AB与CD相交于点O.
(1)若∠AOC= ,则AB⊥CD;
(2)若AB⊥CD,则∠AOC= .
90°
90°
知识点二:垂线的两种画法
(1)利用三角尺的两条直角边或刻度线与所在边的垂直关系画,它的基本步骤是:一靠、二过、三画,即靠已知直线→过定点→画垂线.
(2)利用量角器画,主要是画一个90°的角来得到垂线.
2.(北师7下P41、人教7下P5)如图,过点P画出射线AB或线段AB的垂线.
答案图
解:如图,直线m即为所求作.
结论:平面内,过一点 一条直线与已知直线垂直.
有且只有
知识点三:垂线段的性质
直线外一点与直线上各点连接的所有线段中,
最短.简单说成: .
如图,最短的线段是 .
PO
垂线段最短
垂线段
3.如图,PB⊥m,垂足为B,A为直线m上异于点B的点,则PB<PA的理由是 .
垂线段最短
知识点四:点到直线的距离
如图,过点A作l的垂线,垂足为B,线段 的长度叫做点A到直线l的距离.
注意:距离是一个数量概念.
AB
4.如图,OD⊥BC,垂足为 D,BD=6,OD=8,OB=10,那么点B到OD的距离为 ,点O到BC的距离为 ,
O,B两点之间的距离为 .
10
8
6
5.【例1】(北师7下P43、人教7下P5)如图,某单位要在河岸l上建一个水泵房引水到C处,做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是
.
垂线段最短
6.【例2】(人教7下P8)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
解:因为EO⊥AB,所以∠BOE=90°,
因为∠EOC=35°,所以∠BOC=∠BOE+∠EOC=125°.
所以∠AOD=∠BOC=125°.
7.【例3】如图,分别过点A,B画OA,OB的垂线.
答案图
解:如图,AD,BC即为所求作.
8.【例4】如图,O是直线AB上一点,∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,
并说出理由.
解:(1)因为∠AOC+∠BOC=180°,∠BOC=3∠AOC,
所以3∠AOC+∠AOC=180°.解得∠AOC=45°.
因为OC平分∠AOD,所以∠COD=∠AOC=45°.
(2)OD⊥AB.理由如下:由(1)知,∠AOC=∠COD=45°,
所以∠AOD=∠AOC+∠COD=90°.
所以OD⊥AB.
9.(跨学科融合)(北师7下P42、人教7下P9)如图,这是小明同学在体育课上跳远后留下的脚印,怎样测量他的成绩呢 请你画一画,其依据是 .
解:如图,测量垂线段PH的长即可.
垂线段最短
答案图
10.如图,直线AB,CD相交于点O,OM平分∠AOC,ON⊥OM,∠BOD=45°,求∠CON的度数.
解:因为∠BOD=45°,
所以∠AOC=∠BOD=45°,
因为OM平分∠AOC,
所以∠COM=∠AOC=22.5°.
因为ON⊥OM,所以∠MON=90°,
所以∠CON=∠MON-∠COM=67.5°.
11.如图,已知∠AOB和OA上一点P.
(1)过点P画PC⊥OA,交OB于点C;
(2)过点P画PD⊥OB,垂足是点D.
答案图
解:(1)(2)如图所示.
★12.如图,O为直线AB上一点,OC为射线,OD,OE分别为∠AOC,∠BOC的平分线.
(1)判断OD,OE的位置关系,并说明理由;
(2)若∠AOD=30°,试说明OC平分∠AOE;
(3)若∠AOD∶∠AOE=2∶11,则∠BOE的度数为 .
70°
解:(1)OD⊥OE,理由如下:
因为OD,OE分别为∠AOC,∠BOC的平分线,
所以∠COD=∠AOC,∠COE=∠BOC,
所以∠EOD=∠AOC+∠BOC=∠AOB=90°,
所以OD⊥OE.
(2)因为∠AOD=30°,所以∠COD=30°,
所以∠COE=90°-30°=60°,∠COA=60°,
所以∠COE=∠COA,所以OC平分∠AOE.
布置作业
请完成课后对应习题
感谢大家观看
同课章节目录
