6.3二元一次方程组的应用 冀教版(2024)初中数学七年级下册同步练习(含详细答案解析)
文档属性
| 名称 | 6.3二元一次方程组的应用 冀教版(2024)初中数学七年级下册同步练习(含详细答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 16:58:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3二元一次方程组的应用冀教版( 2024)初中数学七年级下册同步练习(含详细答案解析)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.算法统宗中记载了这样一个问题:“一百馒头一百僧,大和三个更无争,小和三人分一个,大小和尚得几丁?”其大意是:个和尚分个馒头,大和尚人分个馒头,小和尚人分个馒头问大、小和尚各有多少人?设大和尚有人,小和尚有人,则可列方程组为( )
A. B.
C. D.
2.如图,用形状、大小完全相同的长方形纸片在平面直角坐标系中摆成如图所示图案,已知点,则点的坐标为( )
A. B. C. D.
3.“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话数学上的“九宫图”所体现的是一个表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则的值为( )
A. B. C. D.
4.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶公里报废,后轮行驶公里报废,如果在自行车行驶若干公里后,将前后轮进行对换,那么这对轮胎最多可以行驶公里.
A. B. C. D.
5.甲、乙两人从相距千米的两地同时出发,相向而行,经小时相遇如果甲比乙先出发小时,那么在乙出发后经小时两人相遇则甲的速度为千米小时.
A. B. C. D.
6.九章算术盈不足载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出钱,就多了钱:如果每人出钱,就少了钱问一共有多少人?这个物品的价格是多少?设共有人,物品的价格为钱,则可列方程组为( )
A. B. C. D.
7.为了丰富同学们的课余生活,体育委员小强到体育用品商店购羽毛球拍和乒乓球拍,若购副羽毛球拍和副乒乓球拍共需元,小强一共用元购买了副同样的羽毛球拍和副同样的乒乓球拍,若设每副羽毛球拍为元,每副乒乓球拍为元,列二元一次方程组得( )
A. B.
C. D.
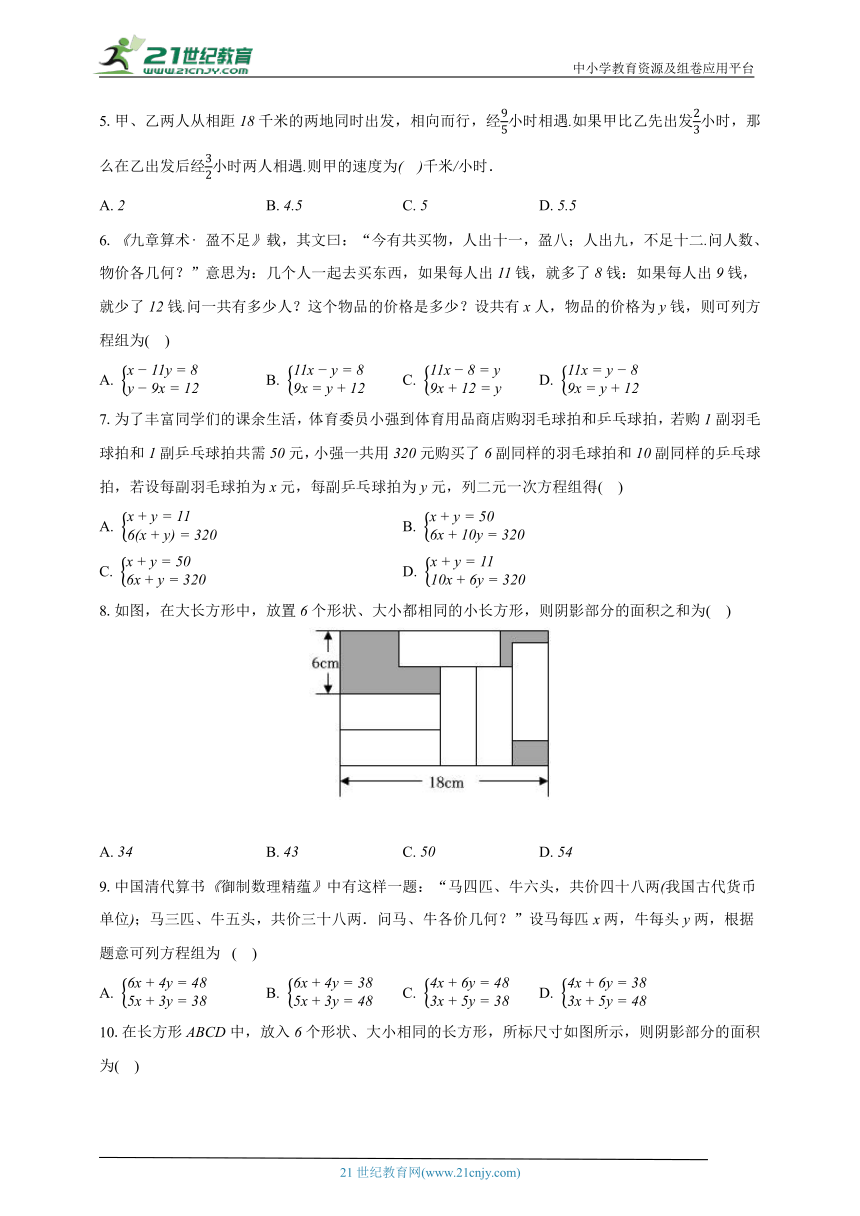
8.如图,在大长方形中,放置个形状、大小都相同的小长方形,则阴影部分的面积之和为( )
A. B. C. D.
9.中国清代算书御制数理精蕴中有这样一题:“马四匹、牛六头,共价四十八两我国古代货币单位;马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为 ( )
A. B. C. D.
10.在长方形中,放入个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
A. B. C. D.
11.下表是某校七九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间 文艺小组活动次数 科技小组活动次数
七年级
八年级
九年级
表格中,的值正确的是( )
A. , B. , C. , D. ,
12.如图所示,在长为、宽为的长方形中,有形状、大小完全相同的个小长方形,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.一个两位数,它的十位数字与个位数字的和是,若把个位与十位数字调换,得到的两位数比原数大,这个两位数是______.
14.孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短引绳度之,余绳四尺五,屈绳量之,不足一尺问木长几何?”译成白话文:“现有一根木头,不知道它的长短用整条绳子去量木头,绳子比木头长尺;将绳子对折后去量,则绳子比木头短尺问木头的长度是多少尺?”设木头的长度为尺,绳子的长度为尺则可列出方程为:______.
15.磁器口古镇,被赞誉为“小重庆”,磁器口的陈麻花更是重庆标志性名片之一.磁器口某门店从陈麻花生产商处采购了原味、麻辣、巧克力三种口味的麻花进行销售,其每袋进价分别是元、元、元,其中原味与麻辣味麻花每袋的销售利润率相同,原味与巧克力味麻花每袋的销售利润相同.经统计,在今年元旦当天,该门店这三种口味的麻花销量是,其销售原味与巧克力味麻花的总利润率是,且巧克力味麻花销售额比原味麻花销售额多元,则今年元旦当天该门店销售这三种口味的麻花的利润共 元.
16.幻方是一种将数字排放在正方形格子中,使其每行、每列和对角线上的数字和都相等的图表.在如图所示的三阶幻方中,的值为 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
某快递公司规定:寄件不超过千克的部分按起步价计费;寄件超过千克的部分按千克计费小丽分别寄快递到北京和上海,收费标准及实际收费如下表:
收费标准
目的地 起步价元 超过千克的部分元千克
上海
北京
实际收费
目的地 质量千克 费用元
上海
北京
求,的值;
若小丽寄千克的快递到上海,则小丽需要付多少钱的快递费?
18.本小题分
如图,某工厂与、两地有公路、铁路相连,这家工厂从地购买一批原料运回工厂,制成新产品再运到地,公路运价为元吨千米,铁路运价为元吨千米若这两次运输共支出公路运费元,铁路运费元问从地购买多少吨原料,用购买的这些原料能制成多少吨新产品?
在的条件下,原料费为每吨元,新产品每吨元,则该工厂这批产品全部售出后获得利润多少元?利润销售额原料费运输费
19.本小题分
某铁路桥长,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了,整列火车完全在桥上的时间共求火车的速度和长度.
20.本小题分
富平柿饼以当地生产的传统名优柿子品种“富平尖柿”为原料,经过清洗削皮、日晒压捏、捏晒整形、定型捂霜等多道工序精细制作而成,因其肉多霜厚、底亮质润深受省内外人们的喜爱某柿子种植户将自家的柿饼做成、两种规格的礼盒进行销售,已知盒规格柿饼的总售价与盒规格柿饼的总售价相同,盒规格的柿饼总售价比盒规格的柿饼总售价多元,求每盒规格柿饼和每盒规格柿饼的售价分别为多少元?
21.本小题分
为了进一步加强学生的校园安全意识,某班开展校园安全知识竞赛活动,去奶茶店购买,两种款式的奶茶作为奖品若买杯款奶茶,杯款奶茶,共需元;若买杯款奶茶,杯款奶茶,共需元奶茶店为了满足市场的需求,推出每杯元的加料服务,顾客在选完款式后可以自主选择加料一份或者不加料.
求款奶茶和款奶茶的销售单价各是多少元;
在不加料的情况下,购买,两种款式的奶茶两种都买,刚好用了元,请问有几种购买方案?
若小华恰好用了元购买,两款奶茶,其中款不加料的数量是总数量的,则款加料的奶茶买了多少杯?
22.本小题分
开学初,小芳和小亮去商店购买中性笔和笔记本,小芳用元钱买了支中性笔和本笔记本;小亮用元钱买了同样的中性笔支和笔记本本.
求每支中性笔和每本笔记本的价格;
校运动会后,班主任拿出元奖励基金交给班长,购买上述价格的中性笔和笔记本共件作为奖品,要求笔记本数不少于中性笔数,共有多少种购买方案,请写出来.
23.本小题分
【问题背景】台大收割机和台小收割机同时工作小时共收割小麦公顷,台大收割机和台小收割机同时工作小时共收割小麦公顷.
【建立模型】设台大收割机和台小收割机每小时各收割小麦公顷和公顷,
用,的式子表示台大收割机和台小收割机同时工作共收割小麦多少公顷;台大收割机和台小收割机同时工作共收割小麦多少公顷;
建立模型,解决实际问题求台大收割机和台小收割机每小时各收割小麦多少公顷?
24.本小题分
为了迎接“亚东会”的到来及提高学生的身体素质,哈美佳外校准备从某体育用品商店一次性购买若干个雪圈儿和雪地足球每个雪圈儿的价格相同,每个雪地足球的价格相同,若购买个雪圈儿和个雪地足球共需元,购买个雪圈儿和个雪地足球共需元.
每个雪圈儿和雪地足球各需多少元?
根据学校的实际情况,需从该商店一次性购买雪圈儿和雪地足球共个,要求购买雪圈儿和雪地足球的总费用不超过元,那么最多可以购买多少个雪圈儿?
25.本小题分
某小区为了绿化环境,计划分两次购进,两种树苗,第一次购进种树苗棵,种树苗棵,共花费元;第二次购进种树苗棵,种树苗棵,共花费元.两次购进的,两种树苗各自的单价均不变
,两种树苗每棵的价格分别是多少元?
因受季节影响,种树苗价格下降,种树苗价格上升,计划购进种树苗棵,种树苗棵,问总费用是多少元?
答案和解析
1.【答案】
【解析】解:设大和尚有人,小和尚有人,
由题意得:,
故选:.
根据题意列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,理解题意建立等量关系是关键.
2.【答案】
【解析】【分析】
设小长方形的长为,宽为,根据点的坐标,即可得出关于,的二元一次方程组,解之即可得出,的值,进而可得出和的值,再结合点所在的象限即可得出点的坐标.
本题考查了二元一次方程组的应用以及坐标与图形性质,找准等量关系,正确列出二元一次方程组是解题的关键.
【解答】
解:设小长方形的长为,宽为,
依题意得:,
解得:
,,
点的坐标为
故选B.
3.【答案】
【解析】解:由题意得:,
解得:,
,
故选:.
根据每行、每列、每条对角线上三个数字之和都相等,列出二元一次方程组,解方程组即可.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
4.【答案】
【解析】解:设每个新轮胎报废时的总磨损量为,
则安装在前轮的轮胎每行驶公里磨损量为,安装在后轮的轮胎每行驶公里的磨损量为,
设一对新轮胎交换位置前走了公里,交换位置后走了公里,
由题意得,
两式相加,得,
解得,
答:轮胎最多可以行驶公里
故选:.
设每个新轮胎报废时的总磨损量为,一对新轮胎交换位置前走了公里,交换位置后走了公里,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
5.【答案】
【解析】解:设甲的速度为千米小时,乙的速度为千米小时,
由题意得:,
解得:,
即甲的速度为千米小时,乙的速度为千米小时,
故选:.
设甲的速度为千米小时,乙的速度为千米小时,根据相向而行,经小时相遇;如果甲比乙先出发小时,那么在乙出发后经小时两人相遇;列出二元一次方程组,解方程组即可.
本题主要考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
6.【答案】
【解析】解:设共有人,物品的价格为钱,根据题意得:
.
故选:.
设共有人,物品的价格为钱,根据“每人出钱,就多了钱;如果每人出钱,就少了钱”列出二元一次方程组即可.
本题主要考查了二元一次方程的应用,理解题意,弄清数量关系是解题关键.
7.【答案】
【解析】解:购副羽毛球拍和副乒乓球拍共需元,用元购买了副同样的羽毛球拍和副同样的乒乓球拍,可得出方程组:
.
故选:.
分别根据等量关系:购副羽毛球拍和副乒乓球拍共需元,用元购买了副同样的羽毛球拍和副同样的乒乓球拍,可得出方程,联立可得出方程组.
此题考查了由实际问题抽象出二元一次方程组的知识,属于基础题,关键是仔细审题得出两个等量关系,建立方程组.
8.【答案】
【解析】解:设每个小长方形的长为,宽为,
根据题意列方程组得:,
解得:,
.
阴影部分的面积之和为.
答:阴影部分的面积之和为.
故选:.
设每个小长方形的长为,宽为,根据各边之间的关系,可得出关于,的二元一次方程组,解之可得出,的值,再利用阴影部分的面积之和大长方形的面积小长方形的面积,即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
9.【答案】
【解析】【分析】
本题主要考查的是由实际问题抽象出二元一次方程组的有关知识.
设马每匹两,牛每头两,根据题意列出方程组求解即可.
【解答】
解:设马每匹两,牛每头两,
由题意得.
10.【答案】
【解析】【分析】
此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.
首先设长方形的长为,宽为,由题意得等量关系:个长个宽;个宽个长个宽,根据等量关系列出方程组,解方程组即可.
【解答】
解:设长方形的长为,宽为,
由题意得:,
解得:,
阴影部分的面积为:,
故选:.
11.【答案】
【解析】解:设文艺小组、科技小组每次活动时间分别为小时,小时, 则符合.
12.【答案】
【解析】【分析】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.设小长方形的长为,宽为,观察图形可得出关于、的二元一次方程组,解之即可求出、的值,再利用阴影部分的面积大长方形的面积小长方形的面积,即可求出结论.
【解答】
解:设小长方形的长为,宽为,
根据题意得:,
解得:,
.
故选:.
13.【答案】
【解析】解:设十位数字为,个位数字为,由题意,:
,
解得,
这个两位数是;
故答案为:.
设十位数字为,个位数字为,根据十位数字与个位数字的和是,把个位与十位数字调换,得到的两位数比原数大,列出方程组进行求解即可.
本题考查二元一次方程组的应用,一元一次方程的应用,关键是根据题意找到等量关系式.
14.【答案】
【解析】解:由题意得:;
故答案为:.
由绳子比木头长尺得:;由绳子对折后比木头短尺得:;组成方程组即可.
本题考查了由实际问题抽象出二元一次方程组,列方程组时要抓住题目中的一些关键性词语,找出等量关系;因为此类题要列二元一次方程组,因此要注意两句话;同时本题要注意绳子对折,即取绳子的二分之一.
15.【答案】
【解析】设原味麻花的销售单价为元,根据题意,得麻辣味麻花的销售单价为元,
巧克力味麻花的销售单价为元.
设今年元旦当天,该门店这三种口味的麻花销量分别是原味袋,麻辣味袋,巧克力味袋,根据题意,得
解得
则今年元旦当天该门店销售这三种口味的麻花的利润为元.
16.【答案】
【解析】【分析】
本题主要考查二元一次方程组的应用,解题的关键是根据幻方的特点列出关于、的算式.
根据“每行、每列和对角线上的数字和都相等”列出方程组并解答.
【解答】
解:根据题意,得.
解得.
所以.
故答案是:.
17.【答案】解:根据题意得:,
解得:.
所以的值为,的值为,
答:的值为,的值为.
根据题意,由得,,.
元,
即小丽需要付元的快递费,
答:小丽需要付元的快递费.
【解析】根据小丽分别寄快递到上海和北京的快递质量和费用,即可得出关于,的二元一次方程组,解之即可得出结论;
由题意列式计算即可.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.【答案】解:设从地购买吨原料,用这些原料能制成吨新产品.
,
解得,
答:购买吨原料,生产吨产品;
元,
答:该工厂这批产品获得利润元.
【解析】设该工厂从地购买了吨原料,用这些原料能制成吨新产品,根据等量关系:两次运输共支出公路运费元;铁路运输元列方程组求解即可;
利用利润销售额原料费运输费即可求解.
本题考查了二元一次方程组的应用,一元一次方程组的应用,借助图形把各个数量之间的关系弄清是解题的关键.
19.【答案】解:设火车的速度为,火车的长度为.
根据题意,得
解这个方程组,得
答:火车的速度为,火车的长度为.
【解析】如果设火车的速度为,火车的长度为,用线段表示大桥和火车的长度,根据题意可画出图.
由图可知:火车行驶的路程等于桥长与火车长的和,火车行驶的路程等于桥长与火车长的差.
20.【答案】解:设每盒规格柿饼的售价为元,每盒规格柿饼的售价为元.
根据题意得,
解得:,
答:每盒规格棒饼的售价为元,每盒规格柿饼的售价为元.
【解析】设每盒规格柿饼的售价为元,每盒规格柿饼的售价为元.根据题意列出二元一次方程组求解,即可解题.
本题考查了二元一次方程组的应用,解答本题的关键是找准等量关系,列出二元一次方程组.
21.【答案】解:设款奶茶的销售单价是元,款奶茶的销售单价是元,
由题意得:,
解得:,
答:款奶茶的销售单价是元,款奶茶的销售单价是元;
设购买种款式的奶茶杯,购买种款式的奶茶杯,
由题意得:,
整理得:,
、均为正整数,
或或,
有种购买方案:
购买种款式的奶茶杯,购买种款式的奶茶杯;
购买种款式的奶茶杯,购买种款式的奶茶杯;
购买种款式的奶茶杯,购买种款式的奶茶杯;
设小华购买的奶茶中,款不加料的奶茶买了杯,款加料的奶茶和款不加料的奶茶买了杯,
则款加料的奶茶买了杯,即杯,
由题意得:,
整理得:,
、、均为正整数,
,
,
答:款加料的奶茶买了杯.
【解析】设款奶茶的销售单价是元,款奶茶的销售单价是元,根据若买杯款奶茶,杯款奶茶,共需元;若买杯型奶茶,杯型奶茶,共需元.列出二元一次方程组,解方程组即可;
设购买种款式的奶茶杯,购买种款式的奶茶杯,根据在不加料的情况下,购买、两种款式的奶茶两种都要,刚好花元,列出二元一次方程,求出正整数解即可;
设小华购买的奶茶中,款不加料的奶茶买了杯,款加料的奶茶和款不加料的奶茶买了杯,则款加料的奶茶买了杯,根据小华恰好用了元购买、两款奶茶,列出二元一次方程,求出正整数解即可.
本题考查了二元一次方程组的应用以及二元一次方程的应用.解题的关键是:找准等量关系,正确列出二元一次方程组;找准等量关系,正确列出二元一次方程;找准等量关系,正确列出二元一次方程.
22.【答案】解:设每支中性笔和每本笔记本的价格分别为元,元,则
,
解得:.
答:每支中性笔和每本笔记本的价格分别为元,元.
设中性笔支,笔记本本,则根据题意,得
,
解得:.
为正整数,
可取,,,,,
共有种购买方案,分别是:
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
【解析】设每支钢笔的价格为元,每本笔记本的价格为元,根据“小芳用元买了支中性笔和本笔记本;小亮用元买了同样的中性笔支和笔记本本”,即可得出关于、的二元一次方程组,解方程组可得出结论.
设中性笔支,笔记本本,根据笔记本数不少于中性笔数,总费用不大于,列出不等式组,再进行求解即可得出答案.
本题考查了二元一次方程组的应用,一元一次不等式组的应用,解题的关键是读懂题意,找到题中的等量关系或不等量关系.
23.【答案】解:由题意得:台大收割机和台小收割机同时工作共收割小麦公顷,
台大收割机和台小收割机同时工作共收割小麦公顷;
由题意得:,
解得,
台大收割机每小时各收割小麦公顷,台小收割机每小时收割小麦公顷.
【解析】根据题意列出代数式即可;
根据“台大收割机和台小收割机同时工作小时共收割小麦公顷,台大收割机和台小收割机同时工作小时共收割小麦公顷”列出二元一次方程组,解方程即可得出答案.
本题考查了列代数式、二元一次方程组的应用,理解题意,正确列出代数式与方程组是解此题的关键.
24.【答案】解:设每个雪圈儿需元,每个雪地足球需元,
根据题意得:,
解得,
答:每个雪圈儿需元,每个雪地足球需元;
设购买个雪圈儿,则可以购买个雪地足球,
依题意得:,
解得:.
又为正整数,
的最大值为,
最多可以购买个雪圈儿.
【解析】设每个雪圈儿需元,每个雪地足球需元,根据“购买个雪圈儿和个雪地足球共需元,购买个雪圈儿和个雪地足球共需元”,即可得出关于,的二元一次方程组,解之即可得出结论;
设购买个雪圈儿,则可以购买个雪地足球,利用总价单价数量,结合总价不超过元,即可得出关于的一元一次不等式,解之取其中的最大整数值即可得出结论.,
本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式.
25.【答案】解:设种树苗每棵的价格是元,种树苗每棵的价格是元,
依题意得:,
解得:.
答:种树苗每棵的价格是元,种树苗每棵的价格是元.
元.
答:总费用为元.
【解析】本题考查了二元一次方程组的应用以及有理数的混合运算,解题的关键是:找准等量关系,正确列出二元一次方程组;利用总价单价数量,求出购买所需总费用.
设种树苗每棵的价格是元,种树苗每棵的价格是元,根据“第一次购进种树苗棵,种树苗棵,共花费元;第二次购进种树苗棵,种树苗棵,共花费元”,即可得出关于,的二元一次方程组,解之即可得出,两种树苗每棵的价格;
利用总价单价数量,即可求出购买所需的总费用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3二元一次方程组的应用冀教版( 2024)初中数学七年级下册同步练习(含详细答案解析)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.算法统宗中记载了这样一个问题:“一百馒头一百僧,大和三个更无争,小和三人分一个,大小和尚得几丁?”其大意是:个和尚分个馒头,大和尚人分个馒头,小和尚人分个馒头问大、小和尚各有多少人?设大和尚有人,小和尚有人,则可列方程组为( )
A. B.
C. D.
2.如图,用形状、大小完全相同的长方形纸片在平面直角坐标系中摆成如图所示图案,已知点,则点的坐标为( )
A. B. C. D.
3.“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话数学上的“九宫图”所体现的是一个表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则的值为( )
A. B. C. D.
4.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶公里报废,后轮行驶公里报废,如果在自行车行驶若干公里后,将前后轮进行对换,那么这对轮胎最多可以行驶公里.
A. B. C. D.
5.甲、乙两人从相距千米的两地同时出发,相向而行,经小时相遇如果甲比乙先出发小时,那么在乙出发后经小时两人相遇则甲的速度为千米小时.
A. B. C. D.
6.九章算术盈不足载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出钱,就多了钱:如果每人出钱,就少了钱问一共有多少人?这个物品的价格是多少?设共有人,物品的价格为钱,则可列方程组为( )
A. B. C. D.
7.为了丰富同学们的课余生活,体育委员小强到体育用品商店购羽毛球拍和乒乓球拍,若购副羽毛球拍和副乒乓球拍共需元,小强一共用元购买了副同样的羽毛球拍和副同样的乒乓球拍,若设每副羽毛球拍为元,每副乒乓球拍为元,列二元一次方程组得( )
A. B.
C. D.
8.如图,在大长方形中,放置个形状、大小都相同的小长方形,则阴影部分的面积之和为( )
A. B. C. D.
9.中国清代算书御制数理精蕴中有这样一题:“马四匹、牛六头,共价四十八两我国古代货币单位;马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为 ( )
A. B. C. D.
10.在长方形中,放入个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
A. B. C. D.
11.下表是某校七九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间 文艺小组活动次数 科技小组活动次数
七年级
八年级
九年级
表格中,的值正确的是( )
A. , B. , C. , D. ,
12.如图所示,在长为、宽为的长方形中,有形状、大小完全相同的个小长方形,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.一个两位数,它的十位数字与个位数字的和是,若把个位与十位数字调换,得到的两位数比原数大,这个两位数是______.
14.孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短引绳度之,余绳四尺五,屈绳量之,不足一尺问木长几何?”译成白话文:“现有一根木头,不知道它的长短用整条绳子去量木头,绳子比木头长尺;将绳子对折后去量,则绳子比木头短尺问木头的长度是多少尺?”设木头的长度为尺,绳子的长度为尺则可列出方程为:______.
15.磁器口古镇,被赞誉为“小重庆”,磁器口的陈麻花更是重庆标志性名片之一.磁器口某门店从陈麻花生产商处采购了原味、麻辣、巧克力三种口味的麻花进行销售,其每袋进价分别是元、元、元,其中原味与麻辣味麻花每袋的销售利润率相同,原味与巧克力味麻花每袋的销售利润相同.经统计,在今年元旦当天,该门店这三种口味的麻花销量是,其销售原味与巧克力味麻花的总利润率是,且巧克力味麻花销售额比原味麻花销售额多元,则今年元旦当天该门店销售这三种口味的麻花的利润共 元.
16.幻方是一种将数字排放在正方形格子中,使其每行、每列和对角线上的数字和都相等的图表.在如图所示的三阶幻方中,的值为 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
某快递公司规定:寄件不超过千克的部分按起步价计费;寄件超过千克的部分按千克计费小丽分别寄快递到北京和上海,收费标准及实际收费如下表:
收费标准
目的地 起步价元 超过千克的部分元千克
上海
北京
实际收费
目的地 质量千克 费用元
上海
北京
求,的值;
若小丽寄千克的快递到上海,则小丽需要付多少钱的快递费?
18.本小题分
如图,某工厂与、两地有公路、铁路相连,这家工厂从地购买一批原料运回工厂,制成新产品再运到地,公路运价为元吨千米,铁路运价为元吨千米若这两次运输共支出公路运费元,铁路运费元问从地购买多少吨原料,用购买的这些原料能制成多少吨新产品?
在的条件下,原料费为每吨元,新产品每吨元,则该工厂这批产品全部售出后获得利润多少元?利润销售额原料费运输费
19.本小题分
某铁路桥长,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了,整列火车完全在桥上的时间共求火车的速度和长度.
20.本小题分
富平柿饼以当地生产的传统名优柿子品种“富平尖柿”为原料,经过清洗削皮、日晒压捏、捏晒整形、定型捂霜等多道工序精细制作而成,因其肉多霜厚、底亮质润深受省内外人们的喜爱某柿子种植户将自家的柿饼做成、两种规格的礼盒进行销售,已知盒规格柿饼的总售价与盒规格柿饼的总售价相同,盒规格的柿饼总售价比盒规格的柿饼总售价多元,求每盒规格柿饼和每盒规格柿饼的售价分别为多少元?
21.本小题分
为了进一步加强学生的校园安全意识,某班开展校园安全知识竞赛活动,去奶茶店购买,两种款式的奶茶作为奖品若买杯款奶茶,杯款奶茶,共需元;若买杯款奶茶,杯款奶茶,共需元奶茶店为了满足市场的需求,推出每杯元的加料服务,顾客在选完款式后可以自主选择加料一份或者不加料.
求款奶茶和款奶茶的销售单价各是多少元;
在不加料的情况下,购买,两种款式的奶茶两种都买,刚好用了元,请问有几种购买方案?
若小华恰好用了元购买,两款奶茶,其中款不加料的数量是总数量的,则款加料的奶茶买了多少杯?
22.本小题分
开学初,小芳和小亮去商店购买中性笔和笔记本,小芳用元钱买了支中性笔和本笔记本;小亮用元钱买了同样的中性笔支和笔记本本.
求每支中性笔和每本笔记本的价格;
校运动会后,班主任拿出元奖励基金交给班长,购买上述价格的中性笔和笔记本共件作为奖品,要求笔记本数不少于中性笔数,共有多少种购买方案,请写出来.
23.本小题分
【问题背景】台大收割机和台小收割机同时工作小时共收割小麦公顷,台大收割机和台小收割机同时工作小时共收割小麦公顷.
【建立模型】设台大收割机和台小收割机每小时各收割小麦公顷和公顷,
用,的式子表示台大收割机和台小收割机同时工作共收割小麦多少公顷;台大收割机和台小收割机同时工作共收割小麦多少公顷;
建立模型,解决实际问题求台大收割机和台小收割机每小时各收割小麦多少公顷?
24.本小题分
为了迎接“亚东会”的到来及提高学生的身体素质,哈美佳外校准备从某体育用品商店一次性购买若干个雪圈儿和雪地足球每个雪圈儿的价格相同,每个雪地足球的价格相同,若购买个雪圈儿和个雪地足球共需元,购买个雪圈儿和个雪地足球共需元.
每个雪圈儿和雪地足球各需多少元?
根据学校的实际情况,需从该商店一次性购买雪圈儿和雪地足球共个,要求购买雪圈儿和雪地足球的总费用不超过元,那么最多可以购买多少个雪圈儿?
25.本小题分
某小区为了绿化环境,计划分两次购进,两种树苗,第一次购进种树苗棵,种树苗棵,共花费元;第二次购进种树苗棵,种树苗棵,共花费元.两次购进的,两种树苗各自的单价均不变
,两种树苗每棵的价格分别是多少元?
因受季节影响,种树苗价格下降,种树苗价格上升,计划购进种树苗棵,种树苗棵,问总费用是多少元?
答案和解析
1.【答案】
【解析】解:设大和尚有人,小和尚有人,
由题意得:,
故选:.
根据题意列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,理解题意建立等量关系是关键.
2.【答案】
【解析】【分析】
设小长方形的长为,宽为,根据点的坐标,即可得出关于,的二元一次方程组,解之即可得出,的值,进而可得出和的值,再结合点所在的象限即可得出点的坐标.
本题考查了二元一次方程组的应用以及坐标与图形性质,找准等量关系,正确列出二元一次方程组是解题的关键.
【解答】
解:设小长方形的长为,宽为,
依题意得:,
解得:
,,
点的坐标为
故选B.
3.【答案】
【解析】解:由题意得:,
解得:,
,
故选:.
根据每行、每列、每条对角线上三个数字之和都相等,列出二元一次方程组,解方程组即可.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
4.【答案】
【解析】解:设每个新轮胎报废时的总磨损量为,
则安装在前轮的轮胎每行驶公里磨损量为,安装在后轮的轮胎每行驶公里的磨损量为,
设一对新轮胎交换位置前走了公里,交换位置后走了公里,
由题意得,
两式相加,得,
解得,
答:轮胎最多可以行驶公里
故选:.
设每个新轮胎报废时的总磨损量为,一对新轮胎交换位置前走了公里,交换位置后走了公里,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
5.【答案】
【解析】解:设甲的速度为千米小时,乙的速度为千米小时,
由题意得:,
解得:,
即甲的速度为千米小时,乙的速度为千米小时,
故选:.
设甲的速度为千米小时,乙的速度为千米小时,根据相向而行,经小时相遇;如果甲比乙先出发小时,那么在乙出发后经小时两人相遇;列出二元一次方程组,解方程组即可.
本题主要考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
6.【答案】
【解析】解:设共有人,物品的价格为钱,根据题意得:
.
故选:.
设共有人,物品的价格为钱,根据“每人出钱,就多了钱;如果每人出钱,就少了钱”列出二元一次方程组即可.
本题主要考查了二元一次方程的应用,理解题意,弄清数量关系是解题关键.
7.【答案】
【解析】解:购副羽毛球拍和副乒乓球拍共需元,用元购买了副同样的羽毛球拍和副同样的乒乓球拍,可得出方程组:
.
故选:.
分别根据等量关系:购副羽毛球拍和副乒乓球拍共需元,用元购买了副同样的羽毛球拍和副同样的乒乓球拍,可得出方程,联立可得出方程组.
此题考查了由实际问题抽象出二元一次方程组的知识,属于基础题,关键是仔细审题得出两个等量关系,建立方程组.
8.【答案】
【解析】解:设每个小长方形的长为,宽为,
根据题意列方程组得:,
解得:,
.
阴影部分的面积之和为.
答:阴影部分的面积之和为.
故选:.
设每个小长方形的长为,宽为,根据各边之间的关系,可得出关于,的二元一次方程组,解之可得出,的值,再利用阴影部分的面积之和大长方形的面积小长方形的面积,即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
9.【答案】
【解析】【分析】
本题主要考查的是由实际问题抽象出二元一次方程组的有关知识.
设马每匹两,牛每头两,根据题意列出方程组求解即可.
【解答】
解:设马每匹两,牛每头两,
由题意得.
10.【答案】
【解析】【分析】
此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.
首先设长方形的长为,宽为,由题意得等量关系:个长个宽;个宽个长个宽,根据等量关系列出方程组,解方程组即可.
【解答】
解:设长方形的长为,宽为,
由题意得:,
解得:,
阴影部分的面积为:,
故选:.
11.【答案】
【解析】解:设文艺小组、科技小组每次活动时间分别为小时,小时, 则符合.
12.【答案】
【解析】【分析】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.设小长方形的长为,宽为,观察图形可得出关于、的二元一次方程组,解之即可求出、的值,再利用阴影部分的面积大长方形的面积小长方形的面积,即可求出结论.
【解答】
解:设小长方形的长为,宽为,
根据题意得:,
解得:,
.
故选:.
13.【答案】
【解析】解:设十位数字为,个位数字为,由题意,:
,
解得,
这个两位数是;
故答案为:.
设十位数字为,个位数字为,根据十位数字与个位数字的和是,把个位与十位数字调换,得到的两位数比原数大,列出方程组进行求解即可.
本题考查二元一次方程组的应用,一元一次方程的应用,关键是根据题意找到等量关系式.
14.【答案】
【解析】解:由题意得:;
故答案为:.
由绳子比木头长尺得:;由绳子对折后比木头短尺得:;组成方程组即可.
本题考查了由实际问题抽象出二元一次方程组,列方程组时要抓住题目中的一些关键性词语,找出等量关系;因为此类题要列二元一次方程组,因此要注意两句话;同时本题要注意绳子对折,即取绳子的二分之一.
15.【答案】
【解析】设原味麻花的销售单价为元,根据题意,得麻辣味麻花的销售单价为元,
巧克力味麻花的销售单价为元.
设今年元旦当天,该门店这三种口味的麻花销量分别是原味袋,麻辣味袋,巧克力味袋,根据题意,得
解得
则今年元旦当天该门店销售这三种口味的麻花的利润为元.
16.【答案】
【解析】【分析】
本题主要考查二元一次方程组的应用,解题的关键是根据幻方的特点列出关于、的算式.
根据“每行、每列和对角线上的数字和都相等”列出方程组并解答.
【解答】
解:根据题意,得.
解得.
所以.
故答案是:.
17.【答案】解:根据题意得:,
解得:.
所以的值为,的值为,
答:的值为,的值为.
根据题意,由得,,.
元,
即小丽需要付元的快递费,
答:小丽需要付元的快递费.
【解析】根据小丽分别寄快递到上海和北京的快递质量和费用,即可得出关于,的二元一次方程组,解之即可得出结论;
由题意列式计算即可.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.【答案】解:设从地购买吨原料,用这些原料能制成吨新产品.
,
解得,
答:购买吨原料,生产吨产品;
元,
答:该工厂这批产品获得利润元.
【解析】设该工厂从地购买了吨原料,用这些原料能制成吨新产品,根据等量关系:两次运输共支出公路运费元;铁路运输元列方程组求解即可;
利用利润销售额原料费运输费即可求解.
本题考查了二元一次方程组的应用,一元一次方程组的应用,借助图形把各个数量之间的关系弄清是解题的关键.
19.【答案】解:设火车的速度为,火车的长度为.
根据题意,得
解这个方程组,得
答:火车的速度为,火车的长度为.
【解析】如果设火车的速度为,火车的长度为,用线段表示大桥和火车的长度,根据题意可画出图.
由图可知:火车行驶的路程等于桥长与火车长的和,火车行驶的路程等于桥长与火车长的差.
20.【答案】解:设每盒规格柿饼的售价为元,每盒规格柿饼的售价为元.
根据题意得,
解得:,
答:每盒规格棒饼的售价为元,每盒规格柿饼的售价为元.
【解析】设每盒规格柿饼的售价为元,每盒规格柿饼的售价为元.根据题意列出二元一次方程组求解,即可解题.
本题考查了二元一次方程组的应用,解答本题的关键是找准等量关系,列出二元一次方程组.
21.【答案】解:设款奶茶的销售单价是元,款奶茶的销售单价是元,
由题意得:,
解得:,
答:款奶茶的销售单价是元,款奶茶的销售单价是元;
设购买种款式的奶茶杯,购买种款式的奶茶杯,
由题意得:,
整理得:,
、均为正整数,
或或,
有种购买方案:
购买种款式的奶茶杯,购买种款式的奶茶杯;
购买种款式的奶茶杯,购买种款式的奶茶杯;
购买种款式的奶茶杯,购买种款式的奶茶杯;
设小华购买的奶茶中,款不加料的奶茶买了杯,款加料的奶茶和款不加料的奶茶买了杯,
则款加料的奶茶买了杯,即杯,
由题意得:,
整理得:,
、、均为正整数,
,
,
答:款加料的奶茶买了杯.
【解析】设款奶茶的销售单价是元,款奶茶的销售单价是元,根据若买杯款奶茶,杯款奶茶,共需元;若买杯型奶茶,杯型奶茶,共需元.列出二元一次方程组,解方程组即可;
设购买种款式的奶茶杯,购买种款式的奶茶杯,根据在不加料的情况下,购买、两种款式的奶茶两种都要,刚好花元,列出二元一次方程,求出正整数解即可;
设小华购买的奶茶中,款不加料的奶茶买了杯,款加料的奶茶和款不加料的奶茶买了杯,则款加料的奶茶买了杯,根据小华恰好用了元购买、两款奶茶,列出二元一次方程,求出正整数解即可.
本题考查了二元一次方程组的应用以及二元一次方程的应用.解题的关键是:找准等量关系,正确列出二元一次方程组;找准等量关系,正确列出二元一次方程;找准等量关系,正确列出二元一次方程.
22.【答案】解:设每支中性笔和每本笔记本的价格分别为元,元,则
,
解得:.
答:每支中性笔和每本笔记本的价格分别为元,元.
设中性笔支,笔记本本,则根据题意,得
,
解得:.
为正整数,
可取,,,,,
共有种购买方案,分别是:
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
方案:购买水笔支,笔记本本.
【解析】设每支钢笔的价格为元,每本笔记本的价格为元,根据“小芳用元买了支中性笔和本笔记本;小亮用元买了同样的中性笔支和笔记本本”,即可得出关于、的二元一次方程组,解方程组可得出结论.
设中性笔支,笔记本本,根据笔记本数不少于中性笔数,总费用不大于,列出不等式组,再进行求解即可得出答案.
本题考查了二元一次方程组的应用,一元一次不等式组的应用,解题的关键是读懂题意,找到题中的等量关系或不等量关系.
23.【答案】解:由题意得:台大收割机和台小收割机同时工作共收割小麦公顷,
台大收割机和台小收割机同时工作共收割小麦公顷;
由题意得:,
解得,
台大收割机每小时各收割小麦公顷,台小收割机每小时收割小麦公顷.
【解析】根据题意列出代数式即可;
根据“台大收割机和台小收割机同时工作小时共收割小麦公顷,台大收割机和台小收割机同时工作小时共收割小麦公顷”列出二元一次方程组,解方程即可得出答案.
本题考查了列代数式、二元一次方程组的应用,理解题意,正确列出代数式与方程组是解此题的关键.
24.【答案】解:设每个雪圈儿需元,每个雪地足球需元,
根据题意得:,
解得,
答:每个雪圈儿需元,每个雪地足球需元;
设购买个雪圈儿,则可以购买个雪地足球,
依题意得:,
解得:.
又为正整数,
的最大值为,
最多可以购买个雪圈儿.
【解析】设每个雪圈儿需元,每个雪地足球需元,根据“购买个雪圈儿和个雪地足球共需元,购买个雪圈儿和个雪地足球共需元”,即可得出关于,的二元一次方程组,解之即可得出结论;
设购买个雪圈儿,则可以购买个雪地足球,利用总价单价数量,结合总价不超过元,即可得出关于的一元一次不等式,解之取其中的最大整数值即可得出结论.,
本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式.
25.【答案】解:设种树苗每棵的价格是元,种树苗每棵的价格是元,
依题意得:,
解得:.
答:种树苗每棵的价格是元,种树苗每棵的价格是元.
元.
答:总费用为元.
【解析】本题考查了二元一次方程组的应用以及有理数的混合运算,解题的关键是:找准等量关系,正确列出二元一次方程组;利用总价单价数量,求出购买所需总费用.
设种树苗每棵的价格是元,种树苗每棵的价格是元,根据“第一次购进种树苗棵,种树苗棵,共花费元;第二次购进种树苗棵,种树苗棵,共花费元”,即可得出关于,的二元一次方程组,解之即可得出,两种树苗每棵的价格;
利用总价单价数量,即可求出购买所需的总费用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
