1.6利用三角函数测高随堂练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 1.6利用三角函数测高随堂练习 北师大版数学九年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:18:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
2.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.01米)( );
A.1366.00米 B.1482.12米 C.1295.93米 D.1508.21米
3.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点处,然后沿斜坡前行到达最佳测量点处,在点处测得塔顶的仰角为,已知斜坡的斜面坡度,且点,,,,在同一平面内,小明同学测得古塔的高度是( )
A. B. C. D.
4.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
6.一个地图上标准比例尺是1∶300000,图上有一条形区域,其面积约为24 cm2 , 则这块区域的实际面积约为( )平方千米.
A.2160 B.216 C.72 D.10.72
7.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
8.使用测倾器测量倾斜角的步骤有:(1)记下此时铅垂线所指的度数;(2)使支杆的中心线、铅垂线和度盘的刻度线重合;(3)转动度盘,使度盘的直径对准目标M;(4)把支杆竖直插入地面.则正确的步骤应为( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1)
C.(4)(2)(3)(1) D.(3)(4)(2)(1)
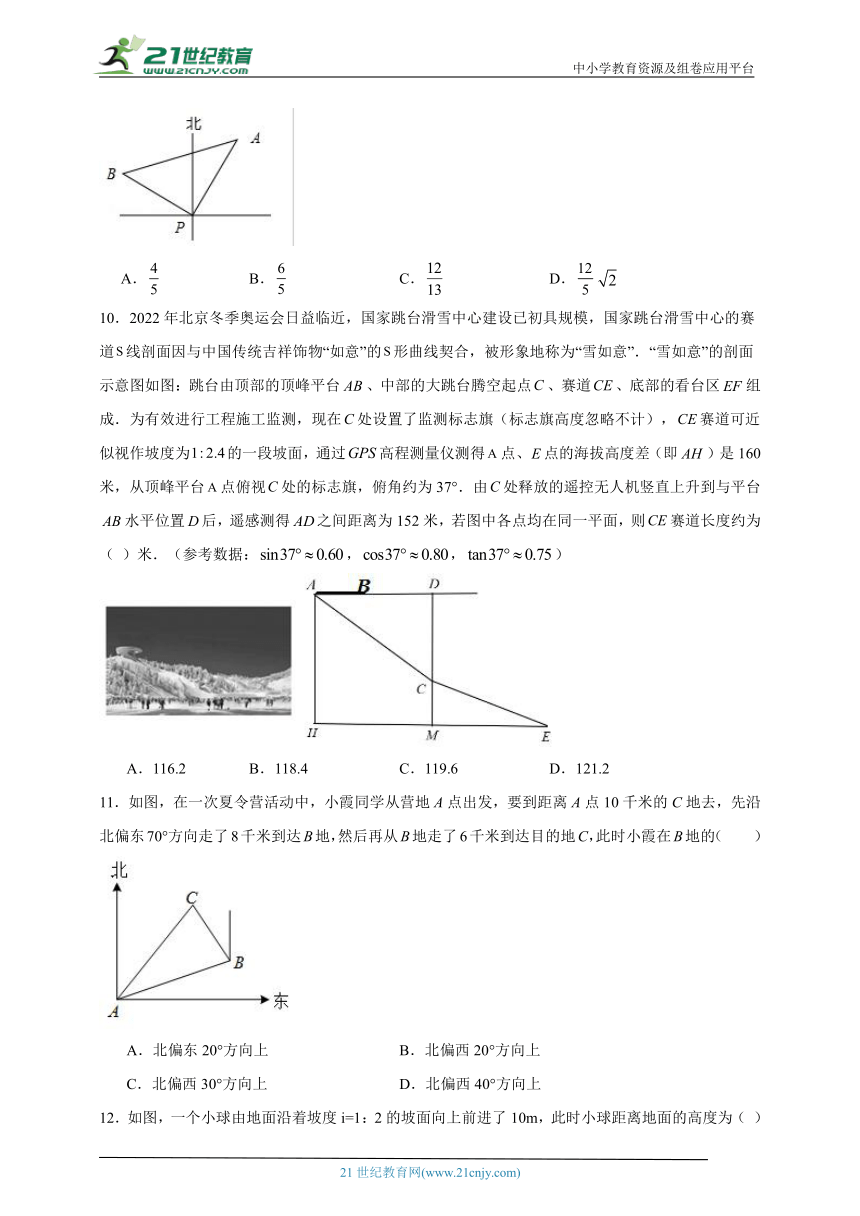
9.某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠BAP=( )
A. B. C. D.
10.2022年北京冬季奥运会日益临近,国家跳台滑雪中心建设已初具规模,国家跳台滑雪中心的赛道线剖面因与中国传统吉祥饰物“如意”的形曲线契合,被形象地称为“雪如意”.“雪如意”的剖面示意图如图:跳台由顶部的顶峰平台、中部的大跳台腾空起点、赛道、底部的看台区组成.为有效进行工程施工监测,现在处设置了监测标志旗(标志旗高度忽略不计),赛道可近似视作坡度为的一段坡面,通过高程测量仪测得点、点的海拔高度差(即)是160米,从顶峰平台点俯视处的标志旗,俯角约为37°.由处释放的遥控无人机竖直上升到与平台水平位置后,遥感测得之间距离为152米,若图中各点均在同一平面,则赛道长度约为( )米.(参考数据:,,)
A.116.2 B.118.4 C.119.6 D.121.2
11.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
12.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.m D.m
二、填空题
13.如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是 海里.(结果保留根号)
14.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成
15.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
16.小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示.他在点O处测得小山顶端的仰角为,小山顶端A在水中倒影的俯角为,已知点O到湖面的距离,A,B,三点共线,,则小山的高度为 m.(光线的折射忽略不计,结果保留根号)
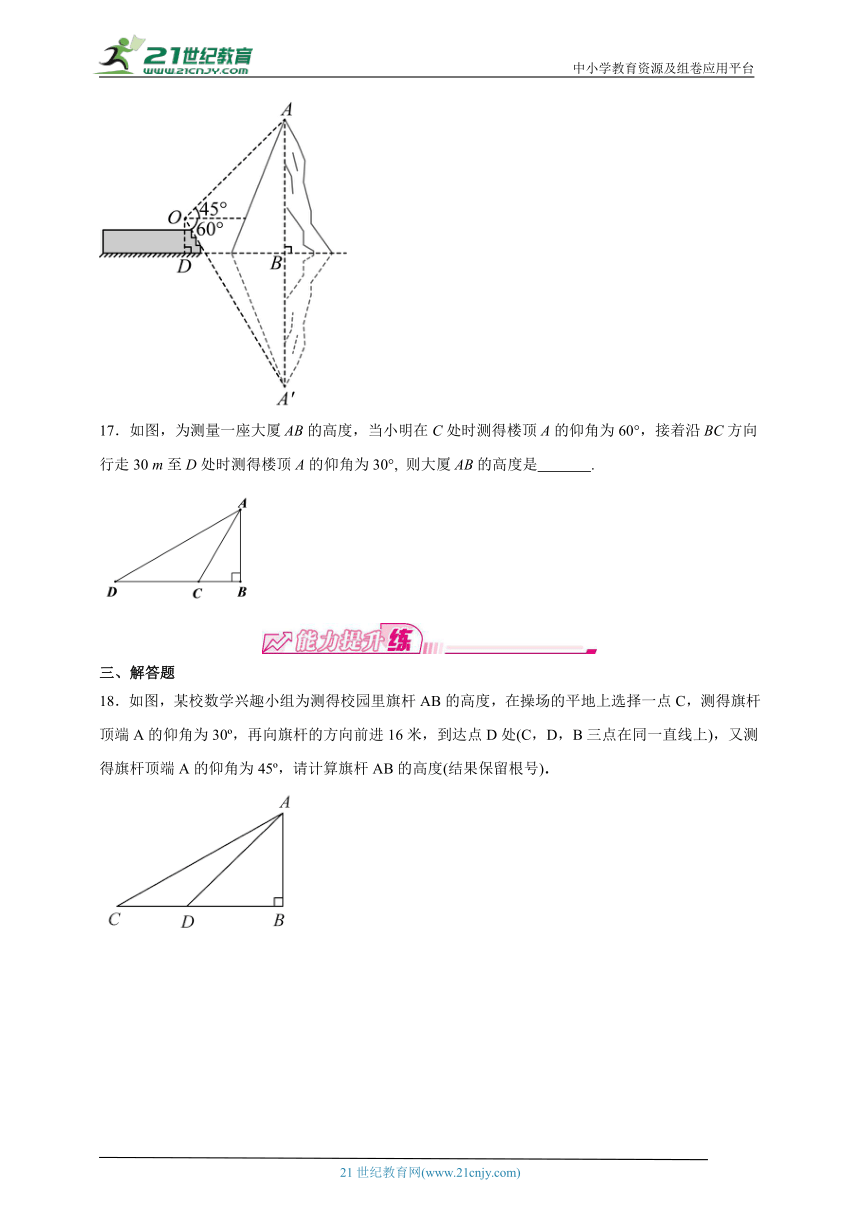
17.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30 m至D处时测得楼顶A的仰角为30°, 则大厦AB的高度是 .
三、解答题
18.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30 ,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45 ,请计算旗杆AB的高度(结果保留根号).
19.如图,某座山的顶部有一座通讯塔,且点A,B,C在同一条直线上,从地面P处测得塔顶C的仰角为,测得塔底B的仰角为.已知通讯塔的高度为,求这座山的高度(结果取整数).参考数据:.
20.图1所示的是某景区的“关帝圣像”,它从2007年1月开始铸造,共用铜吨,铁吨,甚是伟岸壮观.其侧面示意图如图2所示.在处测得圣像顶的仰角为,在点处测得圣像顶的仰角为.已知于点于点米,米,求圣像的高度. (结果保留整数.参考数据:,,)
21.如图,小明家马路对面的商业楼外墙上有一个大型显示屏,小明在自己家楼顶处测得显示屏顶端的仰角为,后退10米到达处测得显示屏底端处的仰角为,已知商业楼的底端与小明家楼底端之间的距离为50米,求显示屏AB的高度.(结果精确到0.1米,参考数据:,,)
22.如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:,,结果保留整数)
23.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
24.举一个生活中运用三角函数解决问题的例子.
《1.6利用三角函数测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D B B A C A C
题号 11 12
答案 B B
1.C
【分析】设BP=x(x≥0),过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,利用正弦三角函数求得S△PBC ,S△ADQ,当两三角形的面积和最小时,四边形的面积最大,根据x≥0即可判断;
【详解】解:如图,过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,设BP=x(x≥0),则AQ=3--x=-x,
∵△ABC是等边三角形,∴∠A=∠B=60°,
∴,,,
∴S△PBC=,
S△ADQ,
S△ABC=,
S△PBC+S△ADQ=≥(x=0时,有最小值),
∴四边形PCDQ面积≤-=,
故选: C.
【点睛】,本题考查了正弦三角函数,等边三角形的性质,根据面积关系正确作出辅助线是解题关键.
2.A
【分析】根据题目所给的度数可判定△ABD是等腰三角形,AD=BD,然后解直角三角形,可求出BE的长和CE的长,从而可求出山高的高度.
【详解】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DF⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500(米).
故选A
【点睛】本题考查直角三角形的应用仰角俯角问题,关键是根据角判断特殊的三角形,直角三角形或者等腰三角形,从而求出解.
3.A
【分析】过作于,于,得到,,设,,根据勾股定理得到,求得,,,于是得到结论.
【详解】解:过作于,于,
,,
斜坡的斜面坡度,
,
设,,
,
,
,,
,
,
,
,
故选:A.
【点睛】本题考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.
4.D
【详解】试题分析:利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
解:在Rt△AFG中,tan∠AFG=,
∴FG==,
在Rt△ACG中,tan∠ACG=,
∴CG==AG.
又∵CG﹣FG=30m,
即AG﹣=30m,
∴AG=15m,
∴AB=(15+2)m.
故选D.
考点:解直角三角形的应用-仰角俯角问题.
5.B
【分析】此题根据题意作图根据锐角三角函数表示出AC,再表示出CD即可求出结果.
【详解】解:根据题意作图如下:
由题意知:AB=m,∠A=,
∴,
∴,
即,
故选:B.
【点睛】此题考查锐角三角函数的应用,主要涉及到正弦和余弦,找准对应边是解题关键.
6.B
【详解】试题分析:设实际面积约为x平方千米,再根据比例尺及相似图形的性质即可列方程求解.
设实际面积约为x平方千米,由题意得
解得
故选B.
考点:比例尺,相似图形的性质
点评:比例尺的问题是中考常见题,一般难度不大,学生只需正确理解比例尺的定义即可.
7.A
【详解】试题分析:在直角△ABC中,∠A=30°,∴BC=AB=×80=40米.故选A.
考点:解直角三角形的应用-坡度坡角问题.
8.C
【分析】根据基本测量理论知识,由测量的基本步骤顺序,即可得到答案.
【详解】解:使用测倾器测量倾斜角的步骤有:把支杆竖直插入地面;使支杆的中心线、铅垂线和度盘的 刻度线重合;转动度盘,使度盘的直径对准目标M;记下此时铅垂线所指的度数;所以正确的顺序是:(4)(2)(3)(1);
故选择:C.
【点睛】本题考查基本的测量理论,要求学生根据几何知识,结合实际操作,做出判断.
9.A
【详解】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A.
10.C
【分析】如图,由题意得: 由 求解 再在中,可得 设 则 由勾股定理可得 从而有 再解方程可得答案.
【详解】解:如图,由题意得:
在中,
在中,
设 则
经检验:符合题意,
故选:
【点睛】本题考查的是解直角三角形的应用,掌握构建直角三角形,利用锐角三角函数解决实际问题是解题的关键.
11.B
【详解】解:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,
根据勾股定理的逆定理可知∠ABC=90°,
根据平行线的性质可得:∠ABE=110°,
则∠CBE=110°-90°=20°,
即点C在点B的北偏西20°方向上.
故选B
12.B
【详解】设小球距离地面的高度为则小球水平移动的距离为 所以解得
13.20
【详解】试题分析:过点B作BD⊥AC,则△ABD为等腰直角三角形,则BD=10海里,在Rt△CBD中,∠CBD=60°,则BC=2BD=20海里.
14.(7,-7)
【详解】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7).
15.80
【分析】过点C作CE⊥AB后,图中将有两个直角三角形.先在△BCE中,利用已知角的正切值求出CE,然后在△CEA中,利用已知角的正切值求出AE即可解决问题.
【详解】
解:作CE⊥AB,垂足为E.
在Rt△BCE中,BE=CD=20,CE=BE÷tan30°=20,
在Rt△ACE中,可得AE=CE×tan60°=20=60,
故AB=AE+EB=60+20=80(米).
故答案为80
【点睛】本题考查仰角、俯角的定义,要求学生能借助角度构造直角三角形并解直角三角形.
16./
【分析】A本题考查解直角三角形,熟练掌握特殊角的三角函数值是解题关键,过点O作于点E,设,则,,根据列方程解出即可.
【详解】解:如图,过点O作于点E,
则,设,
∵,
∴,
∴,
∴,
∵,
∴,即,
∴,
∴.
17.15
【分析】分别在Rt△ACB和Rt△ABD中,利用解直角三角形用AB表示出BC、BD的长,列方程即可解答.
【详解】在Rt△ACB中,∠ACB=60°
∵tan∠ACB= 即tan60°==
∴BC=
在Rt△ABD中,∠ADB=30°
∵tan∠ADB= 即tan30°==
∴BD=
∵CD=30
∴-=30
AB=15
故答案为15
【点睛】本题考查的是解直角三角形的应用,解题关键是在直角三角形中利用三角函数表示出所需线段的长.
18.旗杆AB的高度是(8+8)米.
【分析】根据锐角三角函数可得(CD+DB)×=BD×1,解得BD,从而可以求得AB的高度.
【详解】,解:由题意可得,
CD=16米,
∵AB=CB tan30°,AB=BD tan45°,
∴CB tan30°=BD tan45°,
∴(CD+DB)×=BD×1,
解得BD=8+8,
∴AB=BD tan45°=(8+8)米,
即旗杆AB的高度是(8+8)米.
19.这座山的高度约为
【分析】在中,,在中,,利用,即可列出等式求解.
【详解】解:如图,根据题意,.
在中,,
∴.
在中,,
∴.
∵,
∴.
∴.
答:这座山的高度约为.
【点睛】本题考查三角函数测高,解题的关键在运用三角函数的定义表示出未知边,列出方程.
20.圣像的高度约为米
【分析】设圣像的高度约为米,根据已知中的值用表示的长,根据进而可求出BC的长,从而利用中列出关于的方程,解得的值,即为圣象的高度.
【详解】解:设米,
∵,
∴四边形为矩形,
∴,
在中,,
∴,
∴,
∵米,
∴米,
在中,,
,
∴,
解得,
答:圣像的高度约为米.
【点睛】本题主要考查三角函数.解题的关键在于在直角三角形中,根据三角函数的定义,结合已知条件,列出关于的方程,求解方程即可得解.
21.6.4米
【分析】延长,交于点,则,解,求出的长,解,求出的长,进而求出的长.
【详解】延长,交于点,则,
由题意:,,米,米,
由于四边形是矩形,
∴米,
在中,,
∴米,
∵米,
∴米,
在中,,
∵,
∴,
∴(米).
答:显示屏的高度约为米.
【点睛】本题考查的是利用锐角三角函数知识解直角三角形,构造合适的直角三角形求出相应的线段是解本题的关键.
22.旗杆MN的高度约为13米.
【详解】试题分析:本题主要考查三角函数和解直角三角形,根据题意作点A,C分别向MN作垂线构造两个直角三角形,利用公共边结合三角函数关系进行表示,建立等量关系式列方程求解.
过A作AE⊥MN,垂足为E,过C作CF⊥MN,垂足为F.
设ME=x,Rt△AME中,∠MAE=45°,
∴AE=ME=x,
Rt△MCF中,MF=x+0.2,
CF== (x+0.2),
∵BD=AE+CF,
∴x+ (x+0.2)=30,
∴x≈11,即AE=11,
∴MN=11+1.7=12.7≈13(米),
故旗杆MN的高度约为13米.
23.(1)1520m
(2)下山的速度是每分钟40米
【分析】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,分别解直角三角形即可.
(2)设下山的速度为x m/min,依据题意得,列分式方程求解即可.
【详解】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,
∴BF=200,CE=1000,
∵山坡AB的坡度为,
∴AF=480,
∴AB=520,
过B点作BG⊥CE于G点,
∴四边形BFEG是矩形,
∴EG=BF=200,
∴,
∵山坡BC的坡度为,
∴BG=600,
∴BC=1000,
∴山坡的长为(m) .
(2)∵∠D=30°,∠CED=90°,
∴CD=2000,
设下山的速度为x m/min,依据题意得,
,
解得,,
经检验,是原方程的根,
∴下山的速度是每分钟40米.
【点睛】本题考查了解直角三角形的坡比,坡角问题,熟练掌握化斜为直的解题方法是解题的关键.
24.见详解
【分析】根据生活中的实际例子解答即可.
【详解】解:生活中的例子如:测量大楼或山丘的高度可以用三角函数解答.
【点睛】本题考查解直角三角形的应用,解答本题的关键是测量大楼或山丘的高度可以用三角函数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
2.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.01米)( );
A.1366.00米 B.1482.12米 C.1295.93米 D.1508.21米
3.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点处,然后沿斜坡前行到达最佳测量点处,在点处测得塔顶的仰角为,已知斜坡的斜面坡度,且点,,,,在同一平面内,小明同学测得古塔的高度是( )
A. B. C. D.
4.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
6.一个地图上标准比例尺是1∶300000,图上有一条形区域,其面积约为24 cm2 , 则这块区域的实际面积约为( )平方千米.
A.2160 B.216 C.72 D.10.72
7.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
8.使用测倾器测量倾斜角的步骤有:(1)记下此时铅垂线所指的度数;(2)使支杆的中心线、铅垂线和度盘的刻度线重合;(3)转动度盘,使度盘的直径对准目标M;(4)把支杆竖直插入地面.则正确的步骤应为( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1)
C.(4)(2)(3)(1) D.(3)(4)(2)(1)
9.某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠BAP=( )
A. B. C. D.
10.2022年北京冬季奥运会日益临近,国家跳台滑雪中心建设已初具规模,国家跳台滑雪中心的赛道线剖面因与中国传统吉祥饰物“如意”的形曲线契合,被形象地称为“雪如意”.“雪如意”的剖面示意图如图:跳台由顶部的顶峰平台、中部的大跳台腾空起点、赛道、底部的看台区组成.为有效进行工程施工监测,现在处设置了监测标志旗(标志旗高度忽略不计),赛道可近似视作坡度为的一段坡面,通过高程测量仪测得点、点的海拔高度差(即)是160米,从顶峰平台点俯视处的标志旗,俯角约为37°.由处释放的遥控无人机竖直上升到与平台水平位置后,遥感测得之间距离为152米,若图中各点均在同一平面,则赛道长度约为( )米.(参考数据:,,)
A.116.2 B.118.4 C.119.6 D.121.2
11.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
12.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.m D.m
二、填空题
13.如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是 海里.(结果保留根号)
14.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成
15.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
16.小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示.他在点O处测得小山顶端的仰角为,小山顶端A在水中倒影的俯角为,已知点O到湖面的距离,A,B,三点共线,,则小山的高度为 m.(光线的折射忽略不计,结果保留根号)
17.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30 m至D处时测得楼顶A的仰角为30°, 则大厦AB的高度是 .
三、解答题
18.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30 ,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45 ,请计算旗杆AB的高度(结果保留根号).
19.如图,某座山的顶部有一座通讯塔,且点A,B,C在同一条直线上,从地面P处测得塔顶C的仰角为,测得塔底B的仰角为.已知通讯塔的高度为,求这座山的高度(结果取整数).参考数据:.
20.图1所示的是某景区的“关帝圣像”,它从2007年1月开始铸造,共用铜吨,铁吨,甚是伟岸壮观.其侧面示意图如图2所示.在处测得圣像顶的仰角为,在点处测得圣像顶的仰角为.已知于点于点米,米,求圣像的高度. (结果保留整数.参考数据:,,)
21.如图,小明家马路对面的商业楼外墙上有一个大型显示屏,小明在自己家楼顶处测得显示屏顶端的仰角为,后退10米到达处测得显示屏底端处的仰角为,已知商业楼的底端与小明家楼底端之间的距离为50米,求显示屏AB的高度.(结果精确到0.1米,参考数据:,,)
22.如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:,,结果保留整数)
23.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
24.举一个生活中运用三角函数解决问题的例子.
《1.6利用三角函数测高》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A D B B A C A C
题号 11 12
答案 B B
1.C
【分析】设BP=x(x≥0),过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,利用正弦三角函数求得S△PBC ,S△ADQ,当两三角形的面积和最小时,四边形的面积最大,根据x≥0即可判断;
【详解】解:如图,过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,设BP=x(x≥0),则AQ=3--x=-x,
∵△ABC是等边三角形,∴∠A=∠B=60°,
∴,,,
∴S△PBC=,
S△ADQ,
S△ABC=,
S△PBC+S△ADQ=≥(x=0时,有最小值),
∴四边形PCDQ面积≤-=,
故选: C.
【点睛】,本题考查了正弦三角函数,等边三角形的性质,根据面积关系正确作出辅助线是解题关键.
2.A
【分析】根据题目所给的度数可判定△ABD是等腰三角形,AD=BD,然后解直角三角形,可求出BE的长和CE的长,从而可求出山高的高度.
【详解】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DF⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500(米).
故选A
【点睛】本题考查直角三角形的应用仰角俯角问题,关键是根据角判断特殊的三角形,直角三角形或者等腰三角形,从而求出解.
3.A
【分析】过作于,于,得到,,设,,根据勾股定理得到,求得,,,于是得到结论.
【详解】解:过作于,于,
,,
斜坡的斜面坡度,
,
设,,
,
,
,,
,
,
,
,
故选:A.
【点睛】本题考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.
4.D
【详解】试题分析:利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
解:在Rt△AFG中,tan∠AFG=,
∴FG==,
在Rt△ACG中,tan∠ACG=,
∴CG==AG.
又∵CG﹣FG=30m,
即AG﹣=30m,
∴AG=15m,
∴AB=(15+2)m.
故选D.
考点:解直角三角形的应用-仰角俯角问题.
5.B
【分析】此题根据题意作图根据锐角三角函数表示出AC,再表示出CD即可求出结果.
【详解】解:根据题意作图如下:
由题意知:AB=m,∠A=,
∴,
∴,
即,
故选:B.
【点睛】此题考查锐角三角函数的应用,主要涉及到正弦和余弦,找准对应边是解题关键.
6.B
【详解】试题分析:设实际面积约为x平方千米,再根据比例尺及相似图形的性质即可列方程求解.
设实际面积约为x平方千米,由题意得
解得
故选B.
考点:比例尺,相似图形的性质
点评:比例尺的问题是中考常见题,一般难度不大,学生只需正确理解比例尺的定义即可.
7.A
【详解】试题分析:在直角△ABC中,∠A=30°,∴BC=AB=×80=40米.故选A.
考点:解直角三角形的应用-坡度坡角问题.
8.C
【分析】根据基本测量理论知识,由测量的基本步骤顺序,即可得到答案.
【详解】解:使用测倾器测量倾斜角的步骤有:把支杆竖直插入地面;使支杆的中心线、铅垂线和度盘的 刻度线重合;转动度盘,使度盘的直径对准目标M;记下此时铅垂线所指的度数;所以正确的顺序是:(4)(2)(3)(1);
故选择:C.
【点睛】本题考查基本的测量理论,要求学生根据几何知识,结合实际操作,做出判断.
9.A
【详解】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A.
10.C
【分析】如图,由题意得: 由 求解 再在中,可得 设 则 由勾股定理可得 从而有 再解方程可得答案.
【详解】解:如图,由题意得:
在中,
在中,
设 则
经检验:符合题意,
故选:
【点睛】本题考查的是解直角三角形的应用,掌握构建直角三角形,利用锐角三角函数解决实际问题是解题的关键.
11.B
【详解】解:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,
根据勾股定理的逆定理可知∠ABC=90°,
根据平行线的性质可得:∠ABE=110°,
则∠CBE=110°-90°=20°,
即点C在点B的北偏西20°方向上.
故选B
12.B
【详解】设小球距离地面的高度为则小球水平移动的距离为 所以解得
13.20
【详解】试题分析:过点B作BD⊥AC,则△ABD为等腰直角三角形,则BD=10海里,在Rt△CBD中,∠CBD=60°,则BC=2BD=20海里.
14.(7,-7)
【详解】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7).
15.80
【分析】过点C作CE⊥AB后,图中将有两个直角三角形.先在△BCE中,利用已知角的正切值求出CE,然后在△CEA中,利用已知角的正切值求出AE即可解决问题.
【详解】
解:作CE⊥AB,垂足为E.
在Rt△BCE中,BE=CD=20,CE=BE÷tan30°=20,
在Rt△ACE中,可得AE=CE×tan60°=20=60,
故AB=AE+EB=60+20=80(米).
故答案为80
【点睛】本题考查仰角、俯角的定义,要求学生能借助角度构造直角三角形并解直角三角形.
16./
【分析】A本题考查解直角三角形,熟练掌握特殊角的三角函数值是解题关键,过点O作于点E,设,则,,根据列方程解出即可.
【详解】解:如图,过点O作于点E,
则,设,
∵,
∴,
∴,
∴,
∵,
∴,即,
∴,
∴.
17.15
【分析】分别在Rt△ACB和Rt△ABD中,利用解直角三角形用AB表示出BC、BD的长,列方程即可解答.
【详解】在Rt△ACB中,∠ACB=60°
∵tan∠ACB= 即tan60°==
∴BC=
在Rt△ABD中,∠ADB=30°
∵tan∠ADB= 即tan30°==
∴BD=
∵CD=30
∴-=30
AB=15
故答案为15
【点睛】本题考查的是解直角三角形的应用,解题关键是在直角三角形中利用三角函数表示出所需线段的长.
18.旗杆AB的高度是(8+8)米.
【分析】根据锐角三角函数可得(CD+DB)×=BD×1,解得BD,从而可以求得AB的高度.
【详解】,解:由题意可得,
CD=16米,
∵AB=CB tan30°,AB=BD tan45°,
∴CB tan30°=BD tan45°,
∴(CD+DB)×=BD×1,
解得BD=8+8,
∴AB=BD tan45°=(8+8)米,
即旗杆AB的高度是(8+8)米.
19.这座山的高度约为
【分析】在中,,在中,,利用,即可列出等式求解.
【详解】解:如图,根据题意,.
在中,,
∴.
在中,,
∴.
∵,
∴.
∴.
答:这座山的高度约为.
【点睛】本题考查三角函数测高,解题的关键在运用三角函数的定义表示出未知边,列出方程.
20.圣像的高度约为米
【分析】设圣像的高度约为米,根据已知中的值用表示的长,根据进而可求出BC的长,从而利用中列出关于的方程,解得的值,即为圣象的高度.
【详解】解:设米,
∵,
∴四边形为矩形,
∴,
在中,,
∴,
∴,
∵米,
∴米,
在中,,
,
∴,
解得,
答:圣像的高度约为米.
【点睛】本题主要考查三角函数.解题的关键在于在直角三角形中,根据三角函数的定义,结合已知条件,列出关于的方程,求解方程即可得解.
21.6.4米
【分析】延长,交于点,则,解,求出的长,解,求出的长,进而求出的长.
【详解】延长,交于点,则,
由题意:,,米,米,
由于四边形是矩形,
∴米,
在中,,
∴米,
∵米,
∴米,
在中,,
∵,
∴,
∴(米).
答:显示屏的高度约为米.
【点睛】本题考查的是利用锐角三角函数知识解直角三角形,构造合适的直角三角形求出相应的线段是解本题的关键.
22.旗杆MN的高度约为13米.
【详解】试题分析:本题主要考查三角函数和解直角三角形,根据题意作点A,C分别向MN作垂线构造两个直角三角形,利用公共边结合三角函数关系进行表示,建立等量关系式列方程求解.
过A作AE⊥MN,垂足为E,过C作CF⊥MN,垂足为F.
设ME=x,Rt△AME中,∠MAE=45°,
∴AE=ME=x,
Rt△MCF中,MF=x+0.2,
CF== (x+0.2),
∵BD=AE+CF,
∴x+ (x+0.2)=30,
∴x≈11,即AE=11,
∴MN=11+1.7=12.7≈13(米),
故旗杆MN的高度约为13米.
23.(1)1520m
(2)下山的速度是每分钟40米
【分析】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,分别解直角三角形即可.
(2)设下山的速度为x m/min,依据题意得,列分式方程求解即可.
【详解】(1)过点C作CE⊥AD于E点,过点B作BF⊥AD于F点,
∴BF=200,CE=1000,
∵山坡AB的坡度为,
∴AF=480,
∴AB=520,
过B点作BG⊥CE于G点,
∴四边形BFEG是矩形,
∴EG=BF=200,
∴,
∵山坡BC的坡度为,
∴BG=600,
∴BC=1000,
∴山坡的长为(m) .
(2)∵∠D=30°,∠CED=90°,
∴CD=2000,
设下山的速度为x m/min,依据题意得,
,
解得,,
经检验,是原方程的根,
∴下山的速度是每分钟40米.
【点睛】本题考查了解直角三角形的坡比,坡角问题,熟练掌握化斜为直的解题方法是解题的关键.
24.见详解
【分析】根据生活中的实际例子解答即可.
【详解】解:生活中的例子如:测量大楼或山丘的高度可以用三角函数解答.
【点睛】本题考查解直角三角形的应用,解答本题的关键是测量大楼或山丘的高度可以用三角函数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
