1.5三角函数的应用随堂练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 1.5三角函数的应用随堂练习 北师大版数学九年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 855.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:17:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.5三角函数的应用
学校:___________姓名:___________班级:___________考号:___________
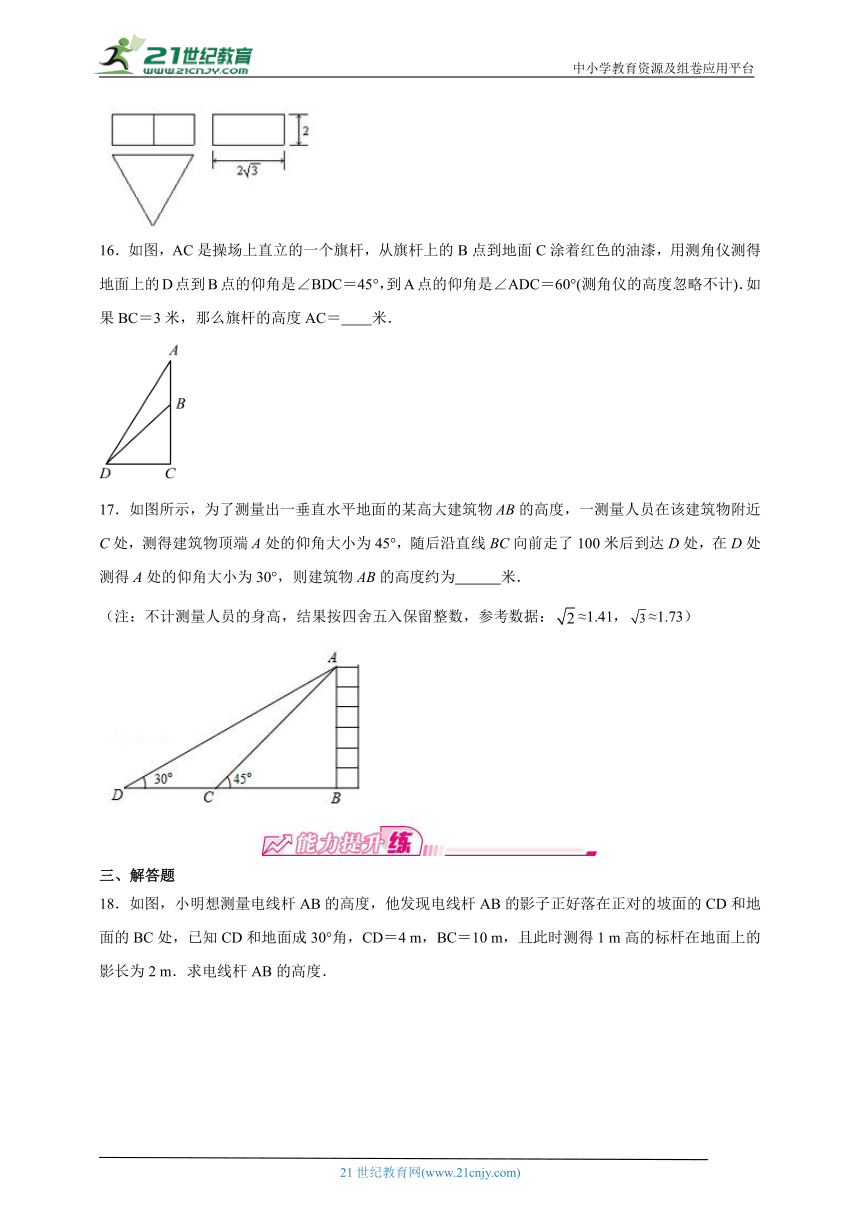
一、单选题
1.如图,梯形护坡石坝的斜坡AB的坡度,坝高BC为2m,则斜坡AB的长是( )
A.m B.m C.m D.6m
2.如图,从树顶A望地面上的C,D两点,测得它们的俯角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于( ).
A.200m B.100m C.100m D.100(+1)m
3.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.2km B.3km C.km D.3km
4.一个长方体木箱沿斜面下滑,当木箱滑至如图所示位置时,.已知木箱高,斜面坡角为度,则木箱端点距地面的高度( )
A.(米) B.(米)
C.(米) D.(米)
5.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为( )
A.米 B.米 C.米 D.米
6.在△ABC中,∠C=90°,,则cotB=( ).
A. B. C. D.
7.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值为( )
A. B. C. D.1
8.如果是锐角,且,那么的值是( ).
A. B. C. D.
9.如图,为了测量山高AC,在水平面B处测得山顶A的仰角是( )
A.∠A B.∠ABC C.∠ABD D.以上都不对
10.如图,小梅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度的方向上离点的处,那么水塔所在的位置到公路的距离是( )
A. B. C. D..
11.若α为锐角,且,则为( )
A. B. C. D.
12.如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
A.12m B.3m C.4m D.12m
二、填空题
13.如图,在某监测点处望见一艘正在作业的渔船在南偏西方向的处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达处,在处观测到在的北偏东方向上,则、之间的距离为 海里.
14.如图,在坡度为1∶2.5的楼梯表面铺地毯,地毯长度至少是 .
15.如图所示为一机器零件的三视图.若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积为 .
16.如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计).如果BC=3米,那么旗杆的高度AC= 米.
17.如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为 米.
(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:≈1.41,≈1.73)
三、解答题
18.如图,小明想测量电线杆AB的高度,他发现电线杆AB的影子正好落在正对的坡面的CD和地面的BC处,已知CD和地面成30°角,CD=4 m,BC=10 m,且此时测得1 m高的标杆在地面上的影长为2 m.求电线杆AB的高度.
19.如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C水平距离300米的D处,测得山顶A的仰角为30°,点B、C、D在同一条直线上,求小山岗的高AB(结果保留整数或保留精确值)(参考数据≈1.732)
20.设计建造一条道路,路基的横断面为梯形ABCD,如图(单位:米).设路基高为h,两侧的坡角分别为和,已知h=2,,,.
(1)求路基底部AB的宽;
(2)修筑这样的路基1000米,需要多少土石方?
21.为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛北偏西并距该岛海里的处待命.位于该岛正西方向处的某外国商船遭到海盗袭击,船长发现在其北偏东的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置处?(结果精确到个位.参考数据:)
22.光明中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50 m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,求建筑物C到公路AB的距离.(已知)
23.如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m,≈1.41,≈1.73)?
24.如图,已知游艇的航速为每时34千米,它从灯塔S的正南方向A处向正东方向航行到B处需1.5时,且在B处测得灯塔S在北偏西65°方向,求B到灯塔S的距离(精确到0.1千米).
《1.5三角函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C D A B C B A
题号 11 12
答案 D C
1.B
【分析】先根据坡比的定义求出AC的长,再根据勾股定理求解即可.
【详解】∵斜坡AB的坡度,坝高BC为2m,
∴1:3=2:AC,
∴AC=6m,
由勾股定理得
AB=m.
故选B.
【点睛】此题主要考查了勾股定理,以及坡度坡角的运用,需注意的是坡度是坡角的正切值,是铅直高度h和水平宽l的比.
2.D
【分析】由所给角的三角函数可以用AB表示出BC,DB长.根据DB-BC=DC求解,可求出树高AB.
【详解】根据俯角的定义,结合题意可得:
BC==AB,BD==AB.
∴CD=BD-BC=(-1)AB=200m.
∴树高AB=100(+1)m.
故选D.
【点睛】本题考查解直角三角形的应用-仰角俯角问题,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
3.B
【详解】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B.
4.C
【分析】过作于,交于,过作于,于,由锐角三角函数定义分别求出和的长,即可求出最后结果.
【详解】解:过作于,交于,过作于,于,如图所示:
则四边形是矩形,
,
在中,,
,
,
,
,,
,
在中,,,
,
,
,
则木箱端点距地面的高度为,
故选:.
【点睛】本题考查解直角三角形的应用一坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
5.D
【分析】根据正切的定义解答即可.
【详解】由题意得,∠B=,
在Rt△ACB中,tanB=,
则BC=米,
故选D.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角和俯角的概念、熟记锐角三角函数的定义是解题的关键.
6.A
【分析】利用三角函数的定义及勾股定理求解.
【详解】如图,sin A=,设BC=4x.则AB=5x.
根据勾股定理可得,
∴.
故选A.
【点睛】求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值.
7.B
【分析】根据特殊角的三角函数值及等腰直角三角形的性质解答.
【详解】解:∵Rt△ABC中,∠C=90°,sinA= ,
∴∠A=∠B=45°,
∴cosB=.
故选B.
【点睛】本题考查等腰直角三角形的性质,特殊角的三角函数值,解题的关键是熟记特殊角的三角函数值.
8.C
【分析】因为,所以利用sin2α+cos2α=1直接解答即可.
【详解】∵
∴
故选:C.
【点睛】考查同角三角函数之间的关系,掌握sin2α+cos2α=1是解题的关键.
9.B
【分析】由仰角的定义,仰角就是视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角
【详解】解:由仰角的定义,得在上图中∠ABC为B处测得山顶A的仰角.
所以选B.
【点睛】本题考查了仰角,熟记仰角、俯角等的定义是基础.
10.A
【分析】如图,在中,由可知,由此即可解决问题.
【详解】解:如图,
由题意,,
,
,
.
故选:A.
【点睛】本题考查解直角三角形,方向角,解题的关键是掌握直角三角形中30度角所对的直角边等于斜边的一半等知识,同时要搞清楚方向角的定义,利用直角三角形性质解决问题,属于中考常考题型.
11.D
【分析】根据同角三角函数的关系,可得α的余弦函数,根据正弦、余弦、正切的关系,可得答案.
【详解】解:由α为锐角,且,得,
,
故选:D.
【点睛】本题考查了同角三角函数的关系,利用了,.
12.C
【分析】先构造直角三角形,在直角三角形中运用三角函数解决问题即可.
【详解】在Rt△ABC中,cos∠A=cos30°=,则AB=m,
故选C.
【点睛】本题主要考查三角函数,熟练运用三角函数是解题的关键.
13.
【分析】由题意可求得∠CAB=90 ,∠ABC=45 ,则△ABC为等腰直角三角形,再由路程=时间×速度求得AC,再通过解该直角三角即可求得BC.
【详解】由题意知,∠CAB=75 +15 =90 ,∠ABC=60 -15 =45 ,AC=60×0.5=30海里,
则有△ABC为等腰直角三角形,
∴BC= ,
故答案为:.
【点睛】本题考查了解直角三角形的应用——方向角,解答的关键是推知△ABC为等腰直角三角形.
14.7米
【详解】将楼梯地毯面分别投影到墙面和地面,易知,楼梯地毯的长度为AB+BC,
坡度=1∶2.5,=5,AB+BC=7.
15.24+8
【详解】∵△ABC是正三角形,
又∵CD⊥AB,CD=2,
∴AC==4,
∴S表面积=4×2×3+2×4××2,
=24+8.
故答案为24+8.
16.3
【详解】试题分析:在Rt△BDC中,∵∠BDC=45°,∴DC=BC=3米.
在Rt△ADC中,∵∠ADC=60°,∴AC=DCtan60°=3×=3(米).
17.137.
【详解】设AB=x米,
在Rt△ABC中,∵∠ACB=45°,
∴BC=AB=x米,则BD=BC+CD=x+100(米),
在Rt△ABD中,∵∠ADB=30°,
∴tan∠ADB=,即,
解得:x=50+50≈137,
即建筑物AB的高度约为137米.
故答案为137.
考点:解直角三角形的应用﹣仰角俯角问题.
18.电线杆AB的高度为m
【分析】如图,可过点D作DE⊥AB于点E,DF⊥BC交BC的延长线于点F,则AB的高度等于线段AE与线段EB之和,线段AE与线段EB可通过图中的已知条件求得,题目得解.
【详解】
解:如图,过点D作DE⊥AB于点E,DF⊥BC交BC的延长线于点F.
∵DC=4 m,∠DCF=30°,
∴DF=2 m,
∴BE=DF=2 m,CF==2 m,
∴ED=BF=BC+CF=(10+2)m.
∵同一时刻的光线是平行的,水平线是平行的,
∴光线与水平线的夹角相等.
又∵标杆与影子构成的角为直角,AE与ED构成的角为直角,
∴AE与影长DE构成的三角形和标杆与影子构成的三角形相似,
∴=,解得AE=(5+)m,
∴AB=AE+BE=(7+)m.
答:电线杆AB的高度为m.
【点睛】本题考查解直角三角形的综合应用,通过作辅助线把AB的高度表示成线段AE与线段EB之和是解题关键.
19.小山岗的高AB为752米
【分析】根据锐角三角函数可以用代数式表示出和的长度,然后根据的值,进而求得的长,本题得以解决.
【详解】解:∵tanα=,
∴设AB=3a,则BC=4a,
∵tan30°=,即=,
解得,a=,
∴AB=3a=≈752,
则小山岗的高AB为752米.
【点睛】本题考查解直角三角形的应用—仰角俯角问题,解题的关键是明确题意,找出所求问题需要的条件.
20.(1)16米;(2)26000立方米.
【分析】(1)分别过D、C作下底AB的垂线,设垂足为E、F.在Rt△ADE和Rt△BCF中,可根据h的长以及坡角的度数或坡比的值,求出AE、BF的长,进而可求得AB的值.
(2)根据(1)得出的梯形下底宽,可求出梯形的面积,进而可求出需要多少土石方.
【详解】(1)过D作DE⊥AB于E,过C作CF⊥AB于F.
Rt△ADE中,∠α=45°,DE=h=2,
∴AE=DE=h=2.
Rt△BCF中,tanβ=,CF=h=2,
∴BF=2CF=4.
故AB=AE+EF+BF=AE+CD+BF=2+10+4=16.
(2)S梯形ABCD=(AB+CD) h=×(10+16)×2=26.
因此所需的土石方数是:26×1000=26000(立方米).
【点睛】坡度、坡角问题通常要转换为解直角三角形的问题,必要时应添加辅助线,构造出直角三角形.
21.28分钟
【分析】首先过点B作BD⊥AC于D,分别在Rt△ABD与Rt△BCD中,利用三角函数的性质,即可求得BC的长,继而求得答案.
【详解】解:过点B作BD⊥AC于D,由图可知,
作于(如图),
在中,
∴
在中,
∴
∴
∴(分钟)
答:我护航舰约需28分钟就可到达该商船所在的位置
【点睛】本题考查了解直角三角形,熟练掌握三角函数是解题的关键.
22.366米
【详解】解:过C作CD⊥AB于D点,
由题意可知AB=50×20=1000m,
∠CAB=30°,∠CBA=45°,AD=,BC=,
∵AD+BD=+ =1000,
解得CD==500()m≈366m
23.16.2m.
【分析】通过投影的知识结合题意构造直角三角形Rt△BEF,根据含角的直角三角形的性质及勾股定理即可求出甲楼的影子在乙楼上有多高.
【详解】设甲楼的影子在乙楼上的最高点为E,作EF⊥AB于F,
在Rt△BFE中,
∵∠BFE=90°,∠BEF=30°,
∴BF=BE,
根据勾股定理,得BF2+EF2=BE2,
∴BF2+242=4BF2,
即BF=8≈13.8m,
∴CE=AF=AB-BF=16.2(m).
【点睛】本题考查了解直角三角形的应用,正确构建直角三角形是解题的关键.
24.56.3千米
【分析】先计算AB的长度,在利用cos25°即可求解SB的长度.
【详解】解:AB=34×1.5=51千米,
∵cos∠SBA=,
∴SB==56.3千米,
故B到灯塔S的距离为56.3千米.
【点睛】本题考查了实际生活与三角函数相结合的能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.5三角函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,梯形护坡石坝的斜坡AB的坡度,坝高BC为2m,则斜坡AB的长是( )
A.m B.m C.m D.6m
2.如图,从树顶A望地面上的C,D两点,测得它们的俯角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于( ).
A.200m B.100m C.100m D.100(+1)m
3.如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A.2km B.3km C.km D.3km
4.一个长方体木箱沿斜面下滑,当木箱滑至如图所示位置时,.已知木箱高,斜面坡角为度,则木箱端点距地面的高度( )
A.(米) B.(米)
C.(米) D.(米)
5.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为( )
A.米 B.米 C.米 D.米
6.在△ABC中,∠C=90°,,则cotB=( ).
A. B. C. D.
7.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值为( )
A. B. C. D.1
8.如果是锐角,且,那么的值是( ).
A. B. C. D.
9.如图,为了测量山高AC,在水平面B处测得山顶A的仰角是( )
A.∠A B.∠ABC C.∠ABD D.以上都不对
10.如图,小梅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度的方向上离点的处,那么水塔所在的位置到公路的距离是( )
A. B. C. D..
11.若α为锐角,且,则为( )
A. B. C. D.
12.如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
A.12m B.3m C.4m D.12m
二、填空题
13.如图,在某监测点处望见一艘正在作业的渔船在南偏西方向的处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达处,在处观测到在的北偏东方向上,则、之间的距离为 海里.
14.如图,在坡度为1∶2.5的楼梯表面铺地毯,地毯长度至少是 .
15.如图所示为一机器零件的三视图.若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积为 .
16.如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计).如果BC=3米,那么旗杆的高度AC= 米.
17.如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为 米.
(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:≈1.41,≈1.73)
三、解答题
18.如图,小明想测量电线杆AB的高度,他发现电线杆AB的影子正好落在正对的坡面的CD和地面的BC处,已知CD和地面成30°角,CD=4 m,BC=10 m,且此时测得1 m高的标杆在地面上的影长为2 m.求电线杆AB的高度.
19.如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C水平距离300米的D处,测得山顶A的仰角为30°,点B、C、D在同一条直线上,求小山岗的高AB(结果保留整数或保留精确值)(参考数据≈1.732)
20.设计建造一条道路,路基的横断面为梯形ABCD,如图(单位:米).设路基高为h,两侧的坡角分别为和,已知h=2,,,.
(1)求路基底部AB的宽;
(2)修筑这样的路基1000米,需要多少土石方?
21.为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛北偏西并距该岛海里的处待命.位于该岛正西方向处的某外国商船遭到海盗袭击,船长发现在其北偏东的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置处?(结果精确到个位.参考数据:)
22.光明中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50 m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,求建筑物C到公路AB的距离.(已知)
23.如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m,≈1.41,≈1.73)?
24.如图,已知游艇的航速为每时34千米,它从灯塔S的正南方向A处向正东方向航行到B处需1.5时,且在B处测得灯塔S在北偏西65°方向,求B到灯塔S的距离(精确到0.1千米).
《1.5三角函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C D A B C B A
题号 11 12
答案 D C
1.B
【分析】先根据坡比的定义求出AC的长,再根据勾股定理求解即可.
【详解】∵斜坡AB的坡度,坝高BC为2m,
∴1:3=2:AC,
∴AC=6m,
由勾股定理得
AB=m.
故选B.
【点睛】此题主要考查了勾股定理,以及坡度坡角的运用,需注意的是坡度是坡角的正切值,是铅直高度h和水平宽l的比.
2.D
【分析】由所给角的三角函数可以用AB表示出BC,DB长.根据DB-BC=DC求解,可求出树高AB.
【详解】根据俯角的定义,结合题意可得:
BC==AB,BD==AB.
∴CD=BD-BC=(-1)AB=200m.
∴树高AB=100(+1)m.
故选D.
【点睛】本题考查解直角三角形的应用-仰角俯角问题,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
3.B
【详解】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B.
4.C
【分析】过作于,交于,过作于,于,由锐角三角函数定义分别求出和的长,即可求出最后结果.
【详解】解:过作于,交于,过作于,于,如图所示:
则四边形是矩形,
,
在中,,
,
,
,
,,
,
在中,,,
,
,
,
则木箱端点距地面的高度为,
故选:.
【点睛】本题考查解直角三角形的应用一坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
5.D
【分析】根据正切的定义解答即可.
【详解】由题意得,∠B=,
在Rt△ACB中,tanB=,
则BC=米,
故选D.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角和俯角的概念、熟记锐角三角函数的定义是解题的关键.
6.A
【分析】利用三角函数的定义及勾股定理求解.
【详解】如图,sin A=,设BC=4x.则AB=5x.
根据勾股定理可得,
∴.
故选A.
【点睛】求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值.
7.B
【分析】根据特殊角的三角函数值及等腰直角三角形的性质解答.
【详解】解:∵Rt△ABC中,∠C=90°,sinA= ,
∴∠A=∠B=45°,
∴cosB=.
故选B.
【点睛】本题考查等腰直角三角形的性质,特殊角的三角函数值,解题的关键是熟记特殊角的三角函数值.
8.C
【分析】因为,所以利用sin2α+cos2α=1直接解答即可.
【详解】∵
∴
故选:C.
【点睛】考查同角三角函数之间的关系,掌握sin2α+cos2α=1是解题的关键.
9.B
【分析】由仰角的定义,仰角就是视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角
【详解】解:由仰角的定义,得在上图中∠ABC为B处测得山顶A的仰角.
所以选B.
【点睛】本题考查了仰角,熟记仰角、俯角等的定义是基础.
10.A
【分析】如图,在中,由可知,由此即可解决问题.
【详解】解:如图,
由题意,,
,
,
.
故选:A.
【点睛】本题考查解直角三角形,方向角,解题的关键是掌握直角三角形中30度角所对的直角边等于斜边的一半等知识,同时要搞清楚方向角的定义,利用直角三角形性质解决问题,属于中考常考题型.
11.D
【分析】根据同角三角函数的关系,可得α的余弦函数,根据正弦、余弦、正切的关系,可得答案.
【详解】解:由α为锐角,且,得,
,
故选:D.
【点睛】本题考查了同角三角函数的关系,利用了,.
12.C
【分析】先构造直角三角形,在直角三角形中运用三角函数解决问题即可.
【详解】在Rt△ABC中,cos∠A=cos30°=,则AB=m,
故选C.
【点睛】本题主要考查三角函数,熟练运用三角函数是解题的关键.
13.
【分析】由题意可求得∠CAB=90 ,∠ABC=45 ,则△ABC为等腰直角三角形,再由路程=时间×速度求得AC,再通过解该直角三角即可求得BC.
【详解】由题意知,∠CAB=75 +15 =90 ,∠ABC=60 -15 =45 ,AC=60×0.5=30海里,
则有△ABC为等腰直角三角形,
∴BC= ,
故答案为:.
【点睛】本题考查了解直角三角形的应用——方向角,解答的关键是推知△ABC为等腰直角三角形.
14.7米
【详解】将楼梯地毯面分别投影到墙面和地面,易知,楼梯地毯的长度为AB+BC,
坡度=1∶2.5,=5,AB+BC=7.
15.24+8
【详解】∵△ABC是正三角形,
又∵CD⊥AB,CD=2,
∴AC==4,
∴S表面积=4×2×3+2×4××2,
=24+8.
故答案为24+8.
16.3
【详解】试题分析:在Rt△BDC中,∵∠BDC=45°,∴DC=BC=3米.
在Rt△ADC中,∵∠ADC=60°,∴AC=DCtan60°=3×=3(米).
17.137.
【详解】设AB=x米,
在Rt△ABC中,∵∠ACB=45°,
∴BC=AB=x米,则BD=BC+CD=x+100(米),
在Rt△ABD中,∵∠ADB=30°,
∴tan∠ADB=,即,
解得:x=50+50≈137,
即建筑物AB的高度约为137米.
故答案为137.
考点:解直角三角形的应用﹣仰角俯角问题.
18.电线杆AB的高度为m
【分析】如图,可过点D作DE⊥AB于点E,DF⊥BC交BC的延长线于点F,则AB的高度等于线段AE与线段EB之和,线段AE与线段EB可通过图中的已知条件求得,题目得解.
【详解】
解:如图,过点D作DE⊥AB于点E,DF⊥BC交BC的延长线于点F.
∵DC=4 m,∠DCF=30°,
∴DF=2 m,
∴BE=DF=2 m,CF==2 m,
∴ED=BF=BC+CF=(10+2)m.
∵同一时刻的光线是平行的,水平线是平行的,
∴光线与水平线的夹角相等.
又∵标杆与影子构成的角为直角,AE与ED构成的角为直角,
∴AE与影长DE构成的三角形和标杆与影子构成的三角形相似,
∴=,解得AE=(5+)m,
∴AB=AE+BE=(7+)m.
答:电线杆AB的高度为m.
【点睛】本题考查解直角三角形的综合应用,通过作辅助线把AB的高度表示成线段AE与线段EB之和是解题关键.
19.小山岗的高AB为752米
【分析】根据锐角三角函数可以用代数式表示出和的长度,然后根据的值,进而求得的长,本题得以解决.
【详解】解:∵tanα=,
∴设AB=3a,则BC=4a,
∵tan30°=,即=,
解得,a=,
∴AB=3a=≈752,
则小山岗的高AB为752米.
【点睛】本题考查解直角三角形的应用—仰角俯角问题,解题的关键是明确题意,找出所求问题需要的条件.
20.(1)16米;(2)26000立方米.
【分析】(1)分别过D、C作下底AB的垂线,设垂足为E、F.在Rt△ADE和Rt△BCF中,可根据h的长以及坡角的度数或坡比的值,求出AE、BF的长,进而可求得AB的值.
(2)根据(1)得出的梯形下底宽,可求出梯形的面积,进而可求出需要多少土石方.
【详解】(1)过D作DE⊥AB于E,过C作CF⊥AB于F.
Rt△ADE中,∠α=45°,DE=h=2,
∴AE=DE=h=2.
Rt△BCF中,tanβ=,CF=h=2,
∴BF=2CF=4.
故AB=AE+EF+BF=AE+CD+BF=2+10+4=16.
(2)S梯形ABCD=(AB+CD) h=×(10+16)×2=26.
因此所需的土石方数是:26×1000=26000(立方米).
【点睛】坡度、坡角问题通常要转换为解直角三角形的问题,必要时应添加辅助线,构造出直角三角形.
21.28分钟
【分析】首先过点B作BD⊥AC于D,分别在Rt△ABD与Rt△BCD中,利用三角函数的性质,即可求得BC的长,继而求得答案.
【详解】解:过点B作BD⊥AC于D,由图可知,
作于(如图),
在中,
∴
在中,
∴
∴
∴(分钟)
答:我护航舰约需28分钟就可到达该商船所在的位置
【点睛】本题考查了解直角三角形,熟练掌握三角函数是解题的关键.
22.366米
【详解】解:过C作CD⊥AB于D点,
由题意可知AB=50×20=1000m,
∠CAB=30°,∠CBA=45°,AD=,BC=,
∵AD+BD=+ =1000,
解得CD==500()m≈366m
23.16.2m.
【分析】通过投影的知识结合题意构造直角三角形Rt△BEF,根据含角的直角三角形的性质及勾股定理即可求出甲楼的影子在乙楼上有多高.
【详解】设甲楼的影子在乙楼上的最高点为E,作EF⊥AB于F,
在Rt△BFE中,
∵∠BFE=90°,∠BEF=30°,
∴BF=BE,
根据勾股定理,得BF2+EF2=BE2,
∴BF2+242=4BF2,
即BF=8≈13.8m,
∴CE=AF=AB-BF=16.2(m).
【点睛】本题考查了解直角三角形的应用,正确构建直角三角形是解题的关键.
24.56.3千米
【分析】先计算AB的长度,在利用cos25°即可求解SB的长度.
【详解】解:AB=34×1.5=51千米,
∵cos∠SBA=,
∴SB==56.3千米,
故B到灯塔S的距离为56.3千米.
【点睛】本题考查了实际生活与三角函数相结合的能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
