1.3 三角函数的计算随堂练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 1.3 三角函数的计算随堂练习 北师大版数学九年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 725.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:25:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.3三角函数的计算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n B.x=m+n C.x>m+n D.x2=m2+n2
2.如图,等腰直角中,,,点在斜边上,且满足,将绕点顺时针方向旋转到的位置,则的大小为( )
A. B.
C. D.
3.已知,则锐角的度数大约为( )
A. B. C. D.
4.在△ABC中,锐角A、B满足|sinA-|+[cos(B-15°)-]2=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.无法确定
5.在实数,,,中,是有理数的是( )
A. B. C. D.
6.已知,则a约为( )
A. B. C. D.
7.已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下),按下的第一个键是( )
A. B. C. D.
8.已知为锐角,且,则 ( )
A. B. C. D.
9.下列计算错误的有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形中,,在上取一点E,使,则度数为( )
A. B. C. D.不能确定
11.在中,,那么的度数是( )
A. B. C. D.
12.用计算器求tanA=0.5234时的锐角A(精确到1°)按键顺序正确的是( )
A.
B.
C.
D.
二、填空题
13.化简 , .
14.在中,若,,,都是锐角,则是 三角形.
15.tan 67.4°≈ .
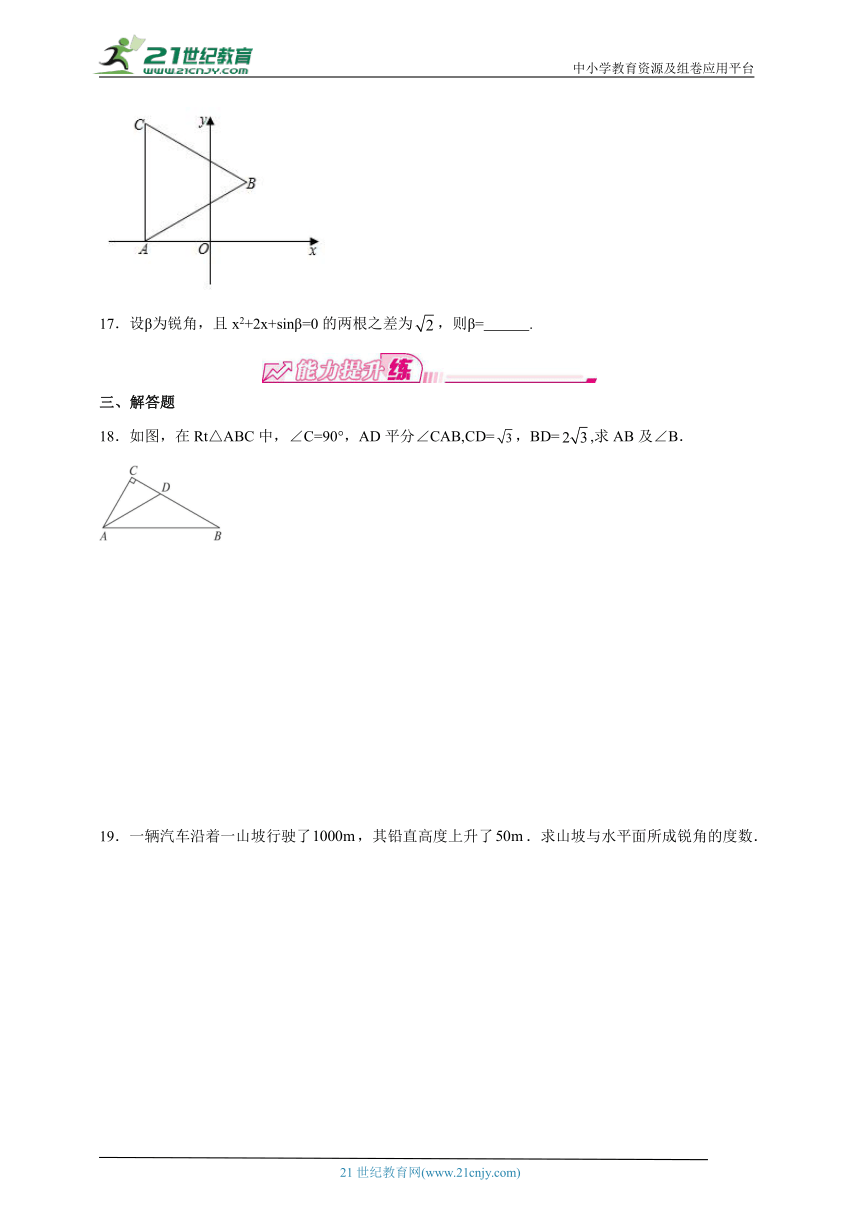
16.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣,0),(,1),连接AB,以AB为边作等边△ABC,则点C的坐标为 .
17.设β为锐角,且x2+2x+sinβ=0的两根之差为,则β= .
三、解答题
18.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=,BD=,求AB及∠B.
19.一辆汽车沿着一山坡行驶了,其铅直高度上升了.求山坡与水平面所成锐角的度数.
20.用计算器求下列锐角三角函数值:
21.计算:﹣sin30°(cos45°﹣sin60°)
22.用计算器求下列锐角三角函数值,并填入表中:
锐角 … … …
随着锐角A的度数不断增大,有怎样的变化趋势?呢?呢?你能说明自己的结论吗?
23.计算:
(1)
(2).
24.tan30°+(+4)0-|-|
《1.3三角函数的计算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C C B D A C B
题号 11 12
答案 C C
1.D
【分析】将△ABM绕点A顺时针旋转90°至△ACN′,连接NN′;证明△AMN≌△ANN′,则有MN=NN′;在Rt△NN'C′中,根据勾股定理可得结论.
【详解】解:∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′,
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选D.
【点睛】此题主要考查了旋转、全等三角形、等腰直角三角形、勾股定理、三角函数等知识点.解题关键是作出辅助线,构造直角三角形是关键.
2.B
【分析】连接OQ,由旋转的性质可得,△BCO△ACQ,则有BO=AQ,, 所以,则有,得到,又因为OC=CQ,可求出,即可求的大小.
【详解】解:连接OQ,
∵,,
∴,
由旋转的性质可得,△BCO△ACQ,
∴,OC=CQ, BO=AQ,,
∴,,
且,
∵,
∴,
∴.
故选B.
【点睛】主要考查了旋转的性质,特殊角的三角函数值等性质的综合应用,注意辅助线的连接是关键.
3.B
【分析】利用计算器计算判断即可.
【详解】用计算器计算可得,.
故选:B.
【点睛】本题考查了锐角三角函数,会用计算器计算三角函数值是解题的关键.
4.C
【分析】根据非负数的性质求出sinA和cos(B-15°)的值,然后求出∠A和∠B的度数,即可判断△ABC的形状.
【详解】∵|sinA-|+[cos(B-15°)-]2=0,
∴,且,
∴sinA=,
∴∠A=45°,
∵,
∴cos(B-15°)=,
∴∠B-15°=30°,
∴∠B=45°,
∴∠C=90°,
∴△ABC为等腰直角三角形,
故选:C.
【点睛】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
5.C
【分析】根据有理数的概念和无理数的概念对各项分析判断即可.
【详解】解:A.,是无理数,故本选项错误;
B.是无理数,故本选项错误;
C.是有理数,故本选项正确;
D. 是无理数,故本选项错误.
故选C.
【点睛】本题考查了实数,特殊角的三角函数值,熟练掌握有理数与无理数的概念是解题的关键.
6.B
【分析】一般先按键“SHIFT”,再按键“tan”,输入“0.3249”,再按键“=”即可得到结果.
【详解】tanα=0.3249,
α约为18°.
故选B.
【点睛】考查了计算器的应用,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
7.D
【详解】根据计算器求锐角的方法即可得结论.
【解答】解:∵已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,sin,0,∴按下的第一个键是2ndF.
故选:D.
【点评】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
8.A
【分析】根据特殊角的三角函数值解答.
【详解】∵为锐角,且,
∴.
故选A.
【点睛】此题考查的是特殊角的三角函数值,属较简单题目.
9.C
【分析】利用特殊角的三角函数值逐个代入计算判断即可;
【详解】解:①,,故左右不相等,错误;
②,正确;③,错误;④,错误.
错误的有3个,
故选择:C
【点睛】本题主要考查特殊三角函数值的计算,熟练掌握特殊角的三角函数值是解题的关键.
10.B
【分析】本题主要考查了矩形的性质,等边对等角,三角形内角和定理,解直角三角形,先由矩形的性质和已知条件证明,然后解直角三角形推出,据此可求出的度数,最后求出的度数即可得到答案.
【详解】解:∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故选:B.
11.C
【分析】此题考查了特殊角的三角函数值,根据,,即可求出答案.
【详解】解:∵是直角三角形,,
∴是锐角,
∵,
∴,
故选:C.
12.C
【详解】试题解析:先按2ndF键,再按三角函数tan键,再依次输入0..5234,最后就可以出来答案.
故选C.
13. 1,
【分析】(1)利用互余两角三角函数间的基本关系计算;(2)利用特殊角的三角函数值计算.
【详解】解:(1)=1
(2)原式=(+)(-)=()2-()2=-=
【点睛】本题考查互余两角三角函数间的基本关系和特殊角的三角函数值,解题关键是熟练掌握基本关系.
14.等边
【分析】直接利用特殊角的三角函数值得出,,进而得出答案.
【详解】解:在中,
,,
且,都是锐角,
,,
是等边三角形.
故答案为:等边.
【点睛】此题主要考查了特殊角的三角函数值,正确记住特殊角的三角函数是解题关键.
15.2.4
【详解】试题解析:先按键“”,再输入“67.4”,最后按键“=”;
故答案为
16.(﹣,2)
【分析】由点A、点B,易知线段AB的长度,∠BAH=30°,而△ABC为等边三角形,得CA⊥x轴,即可知CA的长即为点C的纵坐标,即可求得点C的坐标.
【详解】解:如图,过点B作BH⊥x轴于H,
∵点A,B的坐标分别为(﹣,0),(,1),
∴OA=OH=,BH=1,
∴AH=OA+OH=,
∴AB==2,
∴sin∠BAH==,
∴∠BAH=30°,
∵△ABC为等边三角形,
∴AB=AC=2,
∴∠CAB+∠BAH=90°,
∴点C的纵坐标为2,
∴点C的坐标为(﹣,2).
故答案为:(﹣,2).
【点睛】此题主要考查等边三角形的性质、锐角三角函数,解决此题的关键是掌握等边三角形的性质.
17.30°
【分析】设方程x2+2x+sinβ=0的两根为x1,x2,根据根与系数的关系知,x1+x2=-2,x1x2=sinβ,然后求出(x1-x2)2=(x1+x2)2-4x1x2再把前面的关系式代入得到关于sinβ的方程,解方程即可求出β.
【详解】设方程x2+2x+sinβ=0的两根为,x1+x2=-2,x1x2=sinβ.
由题意知:x1 x2=,
∴(x1-x2)2=(x1+x2)2-4x1x2=4 4sinβ=2,
∴sinβ=,
∴β=30°.
【点睛】本题考查的是三角函数,熟练掌握特殊角度的三角函数值是解题的关键.
18.30°
【分析】过D点作DE⊥AB与E点,设AC=x,∵AD平分∠CAB,而DC⊥AC,DE⊥AB,故△ACD≌△AED,∴AC=AE=x,在Rt△BED,根据勾股定理可得到BE的值,在Rt△ABC,根据勾股定理得出关于x的方程,可解出x的值,然后根据求出sinB的值,得到∠B的角度.
【详解】过D点作DE⊥AB于E点,设AC=x,则AE=x.
在Rt△BED中,得到BE=3,又由AB2=AC2+BC2,得(3+x)2=x2+27,解得x=3,AB=6,
sinB=,
∴∠B=30°.
【点睛】本题主要考查了直角三角形的基本性质和三角函数的概念和基本性质.
19.
【分析】根据正弦公式求出坡脚的正弦值,即可得到山坡与水平面所成锐角的度数.
【详解】解:如图,由题意得AB=1000m,BC=50m,,
∴sinA=,
∴∠A=.
【点睛】此题考查根据锐角三角函数求角度,掌握正弦值的计算公式及题中的数据与坡脚的关系是解题的关键.
20.0.34202;0.939693;0.726543.
【分析】打开科学计算器,启动开机键后,使显示器上方显示DEG(如果没有显示DEG,可以按DR1键),然后按相应的三角比的名称减,再输入锐角的度数,按“=”键后,即可得到相应的三角函数的值(不同计算器各键的功能符号和按键顺序可能不同).
【详解】sin20°≈0.34202;
cos20°≈0.939693;
tan36°≈0.726543.
【点睛】本题考查了学生的操作能力及对基本概念的应用能力,熟析计算器的使用方法是解答本题的关键.
21.
【分析】依据30°、45°、60°角的各种三角函数值,即可得到计算结果.
【详解】解:原式=﹣()
=﹣
=
=
【点睛】本题考查了特殊角的三角函数值,其应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
22.见解析,随着锐角A的度数不断增大,的值不断增大,的值不断减小,的值不断增大
【分析】利用计算器计算出各函数值,再观察表格由此得到答案.
【详解】解:
锐角A … … …
… 0.2588 0.3090 0.3420 0.3746 … 0.9848 0.9903 0.9945 …
… 0.9659 0.9511 0.9397 0.9272 … 0.1736 0.1392 0.1045 …
… 0.2679 0.3249 0.3640 0.4040 … 5.6713 7.1154 9.1544 …
随着锐角A的度数不断增大,的值不断增大,的值不断减小,的值不断增大.
理由:在中,,假定的对边不变,当增大时,必有斜边减小,因此的值增大;假定的邻边不变,当增大时,必有斜边增大,对边增大,因此的值减小,的值增大.
【点睛】此题考查利用三角函数数值表求各角度的三角函数值,根据数据变化总结规律,熟记三角函数值的计算方法是解题的关键.
23.(1);(2).
【分析】(1)先计算特殊角的正弦、余弦、正切值,再计算二次根式的加减乘除运算即可得;
(2)先计算特殊角的正弦、余弦、正切、余切值,再计算二次根式的乘除法与加法即可得.
【详解】(1)原式,
,
,
,
;
(2)原式,
,
,
,
.
【点睛】本题考查了特殊角的三角函数值、二次根式的加减乘除运算,熟记各运算法则是解题关键.
24.1
【分析】分别根据特殊角的三角函数值、零指数幂、绝对值的性质及二次函数化简的法则计算出各数,再根据实数混合运算的法则进行计算即可.
【详解】tan30°+(+4)0-|-|
=3×+1-
=1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3三角函数的计算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )
A.m=n B.x=m+n C.x>m+n D.x2=m2+n2
2.如图,等腰直角中,,,点在斜边上,且满足,将绕点顺时针方向旋转到的位置,则的大小为( )
A. B.
C. D.
3.已知,则锐角的度数大约为( )
A. B. C. D.
4.在△ABC中,锐角A、B满足|sinA-|+[cos(B-15°)-]2=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.无法确定
5.在实数,,,中,是有理数的是( )
A. B. C. D.
6.已知,则a约为( )
A. B. C. D.
7.已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下),按下的第一个键是( )
A. B. C. D.
8.已知为锐角,且,则 ( )
A. B. C. D.
9.下列计算错误的有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形中,,在上取一点E,使,则度数为( )
A. B. C. D.不能确定
11.在中,,那么的度数是( )
A. B. C. D.
12.用计算器求tanA=0.5234时的锐角A(精确到1°)按键顺序正确的是( )
A.
B.
C.
D.
二、填空题
13.化简 , .
14.在中,若,,,都是锐角,则是 三角形.
15.tan 67.4°≈ .
16.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣,0),(,1),连接AB,以AB为边作等边△ABC,则点C的坐标为 .
17.设β为锐角,且x2+2x+sinβ=0的两根之差为,则β= .
三、解答题
18.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=,BD=,求AB及∠B.
19.一辆汽车沿着一山坡行驶了,其铅直高度上升了.求山坡与水平面所成锐角的度数.
20.用计算器求下列锐角三角函数值:
21.计算:﹣sin30°(cos45°﹣sin60°)
22.用计算器求下列锐角三角函数值,并填入表中:
锐角 … … …
随着锐角A的度数不断增大,有怎样的变化趋势?呢?呢?你能说明自己的结论吗?
23.计算:
(1)
(2).
24.tan30°+(+4)0-|-|
《1.3三角函数的计算》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C C B D A C B
题号 11 12
答案 C C
1.D
【分析】将△ABM绕点A顺时针旋转90°至△ACN′,连接NN′;证明△AMN≌△ANN′,则有MN=NN′;在Rt△NN'C′中,根据勾股定理可得结论.
【详解】解:∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′,
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选D.
【点睛】此题主要考查了旋转、全等三角形、等腰直角三角形、勾股定理、三角函数等知识点.解题关键是作出辅助线,构造直角三角形是关键.
2.B
【分析】连接OQ,由旋转的性质可得,△BCO△ACQ,则有BO=AQ,, 所以,则有,得到,又因为OC=CQ,可求出,即可求的大小.
【详解】解:连接OQ,
∵,,
∴,
由旋转的性质可得,△BCO△ACQ,
∴,OC=CQ, BO=AQ,,
∴,,
且,
∵,
∴,
∴.
故选B.
【点睛】主要考查了旋转的性质,特殊角的三角函数值等性质的综合应用,注意辅助线的连接是关键.
3.B
【分析】利用计算器计算判断即可.
【详解】用计算器计算可得,.
故选:B.
【点睛】本题考查了锐角三角函数,会用计算器计算三角函数值是解题的关键.
4.C
【分析】根据非负数的性质求出sinA和cos(B-15°)的值,然后求出∠A和∠B的度数,即可判断△ABC的形状.
【详解】∵|sinA-|+[cos(B-15°)-]2=0,
∴,且,
∴sinA=,
∴∠A=45°,
∵,
∴cos(B-15°)=,
∴∠B-15°=30°,
∴∠B=45°,
∴∠C=90°,
∴△ABC为等腰直角三角形,
故选:C.
【点睛】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
5.C
【分析】根据有理数的概念和无理数的概念对各项分析判断即可.
【详解】解:A.,是无理数,故本选项错误;
B.是无理数,故本选项错误;
C.是有理数,故本选项正确;
D. 是无理数,故本选项错误.
故选C.
【点睛】本题考查了实数,特殊角的三角函数值,熟练掌握有理数与无理数的概念是解题的关键.
6.B
【分析】一般先按键“SHIFT”,再按键“tan”,输入“0.3249”,再按键“=”即可得到结果.
【详解】tanα=0.3249,
α约为18°.
故选B.
【点睛】考查了计算器的应用,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
7.D
【详解】根据计算器求锐角的方法即可得结论.
【解答】解:∵已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,sin,0,∴按下的第一个键是2ndF.
故选:D.
【点评】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
8.A
【分析】根据特殊角的三角函数值解答.
【详解】∵为锐角,且,
∴.
故选A.
【点睛】此题考查的是特殊角的三角函数值,属较简单题目.
9.C
【分析】利用特殊角的三角函数值逐个代入计算判断即可;
【详解】解:①,,故左右不相等,错误;
②,正确;③,错误;④,错误.
错误的有3个,
故选择:C
【点睛】本题主要考查特殊三角函数值的计算,熟练掌握特殊角的三角函数值是解题的关键.
10.B
【分析】本题主要考查了矩形的性质,等边对等角,三角形内角和定理,解直角三角形,先由矩形的性质和已知条件证明,然后解直角三角形推出,据此可求出的度数,最后求出的度数即可得到答案.
【详解】解:∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故选:B.
11.C
【分析】此题考查了特殊角的三角函数值,根据,,即可求出答案.
【详解】解:∵是直角三角形,,
∴是锐角,
∵,
∴,
故选:C.
12.C
【详解】试题解析:先按2ndF键,再按三角函数tan键,再依次输入0..5234,最后就可以出来答案.
故选C.
13. 1,
【分析】(1)利用互余两角三角函数间的基本关系计算;(2)利用特殊角的三角函数值计算.
【详解】解:(1)=1
(2)原式=(+)(-)=()2-()2=-=
【点睛】本题考查互余两角三角函数间的基本关系和特殊角的三角函数值,解题关键是熟练掌握基本关系.
14.等边
【分析】直接利用特殊角的三角函数值得出,,进而得出答案.
【详解】解:在中,
,,
且,都是锐角,
,,
是等边三角形.
故答案为:等边.
【点睛】此题主要考查了特殊角的三角函数值,正确记住特殊角的三角函数是解题关键.
15.2.4
【详解】试题解析:先按键“”,再输入“67.4”,最后按键“=”;
故答案为
16.(﹣,2)
【分析】由点A、点B,易知线段AB的长度,∠BAH=30°,而△ABC为等边三角形,得CA⊥x轴,即可知CA的长即为点C的纵坐标,即可求得点C的坐标.
【详解】解:如图,过点B作BH⊥x轴于H,
∵点A,B的坐标分别为(﹣,0),(,1),
∴OA=OH=,BH=1,
∴AH=OA+OH=,
∴AB==2,
∴sin∠BAH==,
∴∠BAH=30°,
∵△ABC为等边三角形,
∴AB=AC=2,
∴∠CAB+∠BAH=90°,
∴点C的纵坐标为2,
∴点C的坐标为(﹣,2).
故答案为:(﹣,2).
【点睛】此题主要考查等边三角形的性质、锐角三角函数,解决此题的关键是掌握等边三角形的性质.
17.30°
【分析】设方程x2+2x+sinβ=0的两根为x1,x2,根据根与系数的关系知,x1+x2=-2,x1x2=sinβ,然后求出(x1-x2)2=(x1+x2)2-4x1x2再把前面的关系式代入得到关于sinβ的方程,解方程即可求出β.
【详解】设方程x2+2x+sinβ=0的两根为,x1+x2=-2,x1x2=sinβ.
由题意知:x1 x2=,
∴(x1-x2)2=(x1+x2)2-4x1x2=4 4sinβ=2,
∴sinβ=,
∴β=30°.
【点睛】本题考查的是三角函数,熟练掌握特殊角度的三角函数值是解题的关键.
18.30°
【分析】过D点作DE⊥AB与E点,设AC=x,∵AD平分∠CAB,而DC⊥AC,DE⊥AB,故△ACD≌△AED,∴AC=AE=x,在Rt△BED,根据勾股定理可得到BE的值,在Rt△ABC,根据勾股定理得出关于x的方程,可解出x的值,然后根据求出sinB的值,得到∠B的角度.
【详解】过D点作DE⊥AB于E点,设AC=x,则AE=x.
在Rt△BED中,得到BE=3,又由AB2=AC2+BC2,得(3+x)2=x2+27,解得x=3,AB=6,
sinB=,
∴∠B=30°.
【点睛】本题主要考查了直角三角形的基本性质和三角函数的概念和基本性质.
19.
【分析】根据正弦公式求出坡脚的正弦值,即可得到山坡与水平面所成锐角的度数.
【详解】解:如图,由题意得AB=1000m,BC=50m,,
∴sinA=,
∴∠A=.
【点睛】此题考查根据锐角三角函数求角度,掌握正弦值的计算公式及题中的数据与坡脚的关系是解题的关键.
20.0.34202;0.939693;0.726543.
【分析】打开科学计算器,启动开机键后,使显示器上方显示DEG(如果没有显示DEG,可以按DR1键),然后按相应的三角比的名称减,再输入锐角的度数,按“=”键后,即可得到相应的三角函数的值(不同计算器各键的功能符号和按键顺序可能不同).
【详解】sin20°≈0.34202;
cos20°≈0.939693;
tan36°≈0.726543.
【点睛】本题考查了学生的操作能力及对基本概念的应用能力,熟析计算器的使用方法是解答本题的关键.
21.
【分析】依据30°、45°、60°角的各种三角函数值,即可得到计算结果.
【详解】解:原式=﹣()
=﹣
=
=
【点睛】本题考查了特殊角的三角函数值,其应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
22.见解析,随着锐角A的度数不断增大,的值不断增大,的值不断减小,的值不断增大
【分析】利用计算器计算出各函数值,再观察表格由此得到答案.
【详解】解:
锐角A … … …
… 0.2588 0.3090 0.3420 0.3746 … 0.9848 0.9903 0.9945 …
… 0.9659 0.9511 0.9397 0.9272 … 0.1736 0.1392 0.1045 …
… 0.2679 0.3249 0.3640 0.4040 … 5.6713 7.1154 9.1544 …
随着锐角A的度数不断增大,的值不断增大,的值不断减小,的值不断增大.
理由:在中,,假定的对边不变,当增大时,必有斜边减小,因此的值增大;假定的邻边不变,当增大时,必有斜边增大,对边增大,因此的值减小,的值增大.
【点睛】此题考查利用三角函数数值表求各角度的三角函数值,根据数据变化总结规律,熟记三角函数值的计算方法是解题的关键.
23.(1);(2).
【分析】(1)先计算特殊角的正弦、余弦、正切值,再计算二次根式的加减乘除运算即可得;
(2)先计算特殊角的正弦、余弦、正切、余切值,再计算二次根式的乘除法与加法即可得.
【详解】(1)原式,
,
,
,
;
(2)原式,
,
,
,
.
【点睛】本题考查了特殊角的三角函数值、二次根式的加减乘除运算,熟记各运算法则是解题关键.
24.1
【分析】分别根据特殊角的三角函数值、零指数幂、绝对值的性质及二次函数化简的法则计算出各数,再根据实数混合运算的法则进行计算即可.
【详解】tan30°+(+4)0-|-|
=3×+1-
=1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
