3.4简单的图案设计随堂练习 北师大版数学八年级下册(含解析)
文档属性
| 名称 | 3.4简单的图案设计随堂练习 北师大版数学八年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:27:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4简单的图案设计
学校:___________姓名:___________班级:___________考号:___________
一、单选题
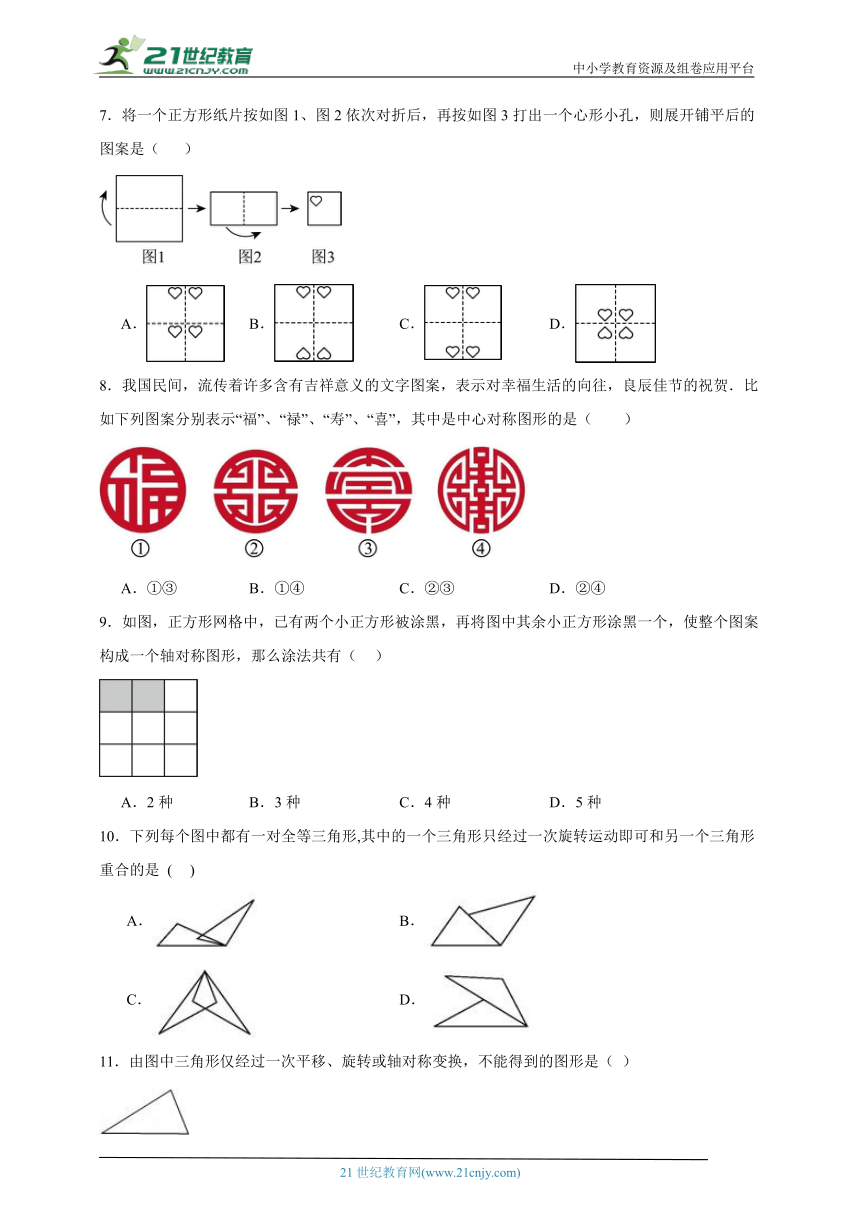
1.下面的图形能拼成正方形的是( ).
A. B. C.
2.下列图形中不是由平移设计的是( )
A. B. C. D.
3.给出下列图形:(1)角;(2)直角三角形;(3)等腰三角形;(4)平行四边形;(5)圆.其中为中心对称图形的是( )
A.(4)(5) B.(2)(3)(5) C.(3)(4) D.(1)(3)(4)(5)
4.“小小竹排水中游,巍巍青山两岸走”所描绘的图形变换主要是 ( )
A.平移变换 B.旋转变换 C.轴对称变换 D.中心对称
5.如图,图案(1)变成图案(2)是由下列哪种变换而成的( )
A.平移变换 B.轴对称变换 C.旋转变换 D.相似变换
6.下列四张扑克牌中,属于中心对称图形的是 ( )
A.红桃7 B.方块4 C.梅花6 D.黑桃5
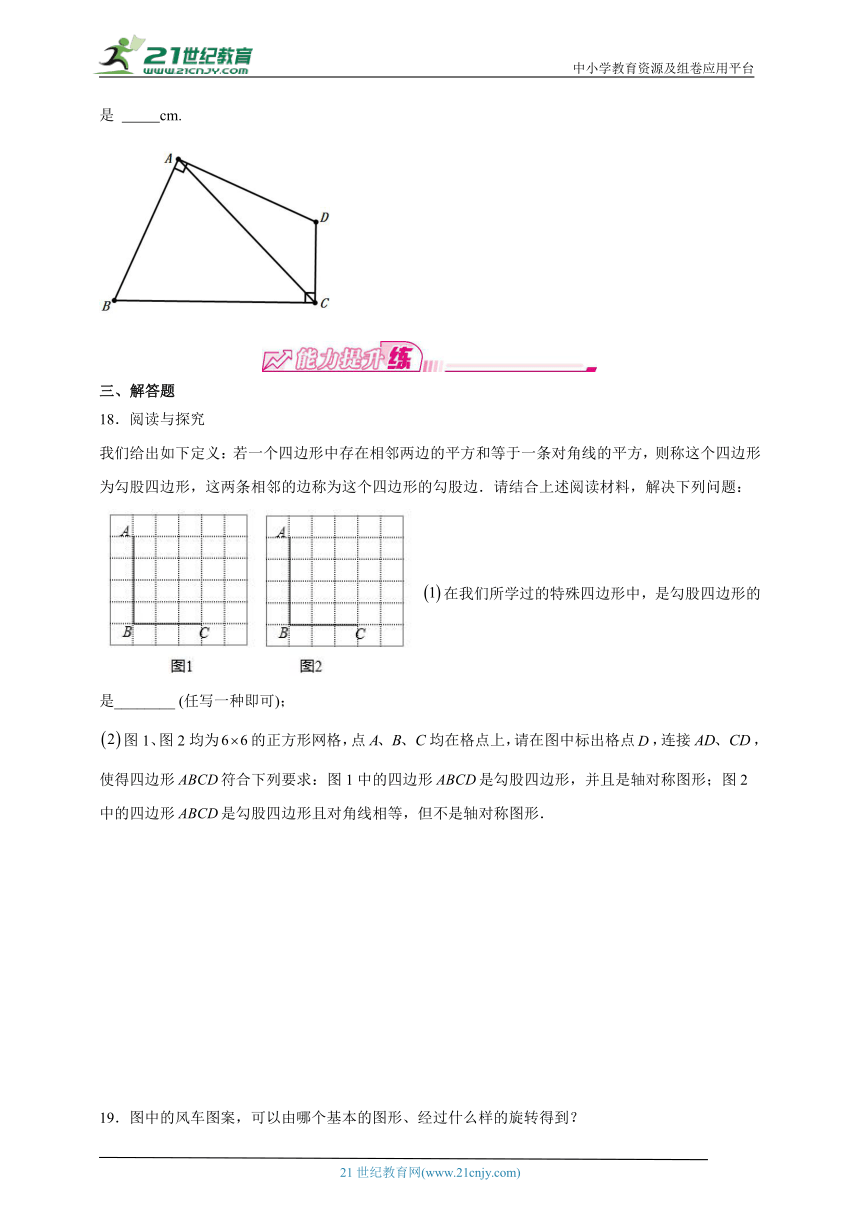
7.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
8.我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
9.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.2种 B.3种 C.4种 D.5种
10.下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是 ( )
A. B.
C. D.
11.由图中三角形仅经过一次平移、旋转或轴对称变换,不能得到的图形是( )
A. B. C. D.
12.下列图案中,可以看成由某一个基本图形通过平移形成的是( )
A. B. C. D.
二、填空题
13.如图, 在平面直角坐标系xOy中, △OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程 .
14.如图,可以看作是一个基础图形绕着中心旋转次而生成的,则每次旋转的度数是 .
15.如图,将左边的图案变成右边的图案的操作是 .
16.如图所示,在中,,将绕点顺时针旋转60°得到,与交于点,则 °,直线与所夹锐角的度数为 .
17.如图,四边形ABCD中,∠BAD=∠BCD=900,AB=AD,若四边形ABCD的面积是24cm2.则AC长是 cm.
三、解答题
18.阅读与探究
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:
在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可);
图1、图2均为的正方形网格,点均在格点上,请在图中标出格点,连接,使得四边形符合下列要求:图1中的四边形是勾股四边形,并且是轴对称图形;图2中的四边形是勾股四边形且对角线相等,但不是轴对称图形.
19.图中的风车图案,可以由哪个基本的图形、经过什么样的旋转得到?
20.图1,图2都是由边长为1的小正方形构成的网格,的三个顶点都在格点上,请在该的网格中,分别按下列要求画一个与有公共边的三角形:
(1)使得所画出的三角形和组成一个轴对称图形.
(2)使得所画出的三角形和组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
21.在的方格内选5个小正方形.
(1)在图1中,让它们以虚线为对称轴,组成一个轴对称图形;在图2中,让它们以虚线为对称轴组成一个轴对称图形;在图3中,让它们构成一个中心对称图形.请在图中画出你的这3种方案.(每个的方格内限画一种)
要求:①5个小正方形必须相连在一起(有公共边或公共顶点视为相连);②将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形能够重合,视为一种方案)
(2)在你所画得三个图中,最喜欢的是哪一个?简要说明理由.
22.如图,下面的图案是由什么基本图案经怎样的旋转得到的?
23.图①、图②均为的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以点A,B,C,D为顶点的四边形,使其为轴对称图形,但不是中心对称图形(画一个即可);
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
24.用四块如图1所示的正方形瓷砖拼成一个新的正方形,请你在图2,、图3、图4中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
《3.4简单的图案设计》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A A C B B D A D
题号 11 12
答案 B C
1.C
【分析】根据正方形的特点可知,两个直角边不相等的直角三角形不能拼成正方形;两个完全一样的正方形不能拼成正方形;选项C的图形可以拼成正方形.据此选择.
【详解】能拼成正方形的是:
故选:C.
【点睛】本题主要考查图形的拼组,关键掌握正方形的特征.
2.D
【分析】根据平移设计图案的定义即可依次判断.
【详解】A、B、C均是平移设计,D为旋转设计,
故选D.
【点睛】此题主要考查平移设计图案,解题的关键是熟知平移设计图案的特点.
3.A
【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;根据中心对称图形的定义,可得角旋转后无法与原角重合,即可进行判断,同理,即可判断其它各项是否为中心对称图形.
【详解】角不是中心对称图形,故(1)不是中心对称图形;
直角三角形不一定是中心对称图形,故(2)不一定是中心对称图形;
等腰三角形不一定是中心对称图形,故(3)不一定是中心对称图形;
平行四边形是中心对称图形,故(4)是中心对称图形;
圆是中心对称图形,故(5)是中心对称图形.
故是中心对称图形的是(4)(5).
故选A.
【点睛】此题考查中心对称图形的性质,解题关键在于掌握其性质.
4.A
【分析】根据诗歌知是小舟在水中行走,故为平移变换.
【详解】根据诗歌知是小舟在水中行走,故为平移变换,故选A.
【点睛】此题主要考查图形变换的类型.
5.C
【分析】图案旋转变换具备三个要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
【详解】根据观察可知,图案(1)变成图案(2)是由旋转变换而成的.
故选 C.
【点睛】本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
6.B
【详解】A选项:红桃7不是中心对称的图形;
B选项:方块4是中心对称的图形;
C选项:梅花6不是中心对称的图形;
D选项:黑桃5不是中心对称的图形;
故选B.
【点睛】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
7.B
【分析】根据题中所给剪纸方法,进行手动操作,答案就能很直观的呈现.
【详解】按照图中顺序进行操作,展开后心形图案应该靠近正方形上下两边,且关于中间折线对称,故只有B选项符合.
故选B.
【点睛】本题考查剪纸问题,解决此类问题要熟知轴对称图形的特点,关键是准确的找到对称轴,一般的方法是动手操作,拿张纸按照题中的要求进行操作.
8.D
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.
【详解】解:①不是中心对称图形,故本选项不合题意;
②是中心对称图形,故本选项符合题意;
③不是中心对称图形,故本选项不合题意;
④是中心对称图形,故本选项符合题意;
故选:D.
【点睛】本题考查了中心对称图形的定义,熟悉掌握概念是解题的关键
9.A
【详解】试题解析:如图,
有2种方法.
故选A.
10.D
【详解】试题分析:根据旋转的性质以及轴对称变换性质分别分析得出即可.
解:A、无法借助旋转得到,故此选项错误;
B、无法借助旋转得到,故此选项错误;
C、可以借助轴对称得到,故此选项错误;
D、可以只经过一次旋转运动即可和另一个三角形,故此选项正确.
故选D.
点评:此题主要考查了利用旋转设计图案,掌握旋转的性质是解题关键.
11.B
【详解】试题分析:根据平移、旋转和轴对称的性质即可得出正确结果.
解:A、经过平移可得到上图,故选项错误;
B、经过平移、旋转或轴对称变换后,都不能得到上图,故选项正确;
C、经过轴对称变换可得到上图,故选项错误;
D、经过旋转可得到上图,故选项错误.
故选B.
点评:本题考查了几何变换的类型,平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是沿某条直线翻折得到新图形.观察时要紧扣图形变换特点,进行分析判断.
12.C
【分析】本题考查了利用平移设计图案,确定一个基本图案,按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案,进而可得答案.
【详解】解:A、不能看成由某一个基本图形通过平移形成的,故不符合题意;
B、不能看成由某一个基本图形通过平移形成的,故不符合题意;
C、能看成由某一个基本图形通过平移形成的,故符合题意;
D、不能看成由某一个基本图形通过平移形成的,故不符合题意;
故选:C.
13.将△AOB顺时针旋转90°,再向左平移2个单位长度
【分析】根据平移、旋转的性质即可得到由△AOB得到△OCD的过程.
【详解】解:将△AOB顺时针旋转90°,再向左平移2个单位长度得到△OCD,
故答案为:将△AOB顺时针旋转90°,再向左平移2个单位长度.
【点睛】本题考查了坐标与图形变化-旋转,坐标与图形变化-平移,解题时需要注意:平移的距离等于对应点连线的长度.
14.
【详解】试题分析:∵一个周角是360度,等腰直角三角形的一个锐角是45度,
∴如图,是由一个等腰直角三角形每次旋转45度,且旋转8次形成的.
∴每次旋转的度数是45°.
故答案是45°.
考点:旋转的性质.
15.旋转
【分析】根据图形旋转的性质即可得出结论.
【详解】解:将左边的图案绕图案中的长方形中心逆时针旋转即可得到右边的图案.
故答案为:旋转.
【点睛】本题考查的是几何变换的类型,熟知图形旋转的性质是解答此题的关键.
16. 90 60°
【分析】先根据旋转的性质得∠CAE=60°,再利用三角形内角和定理计算出∠AFC=90°,延长CB交DE于G,在中即可求得∠EGF=60°.
【详解】∵△ABC绕点A顺时针旋转60°得△ADE,且∠C=30°,
∴∠CAE=60°,∠AED=∠C =30°,
在中,,
∴∠AFB=;
延长CB交DE于G,
在中,∠AED=∠C =30,∠EFG= =,
∴,
∴直线与所夹锐角的度数为,
故答案为:,.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
17.4
【分析】过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,利用三个角为直角的四边形为矩形得到AECF为矩形,利用矩形得四个角为直角得到∠EAF为直角,利用等式的性质得到∠DAF=∠BAE,再由一对直角相等,AB=AD,利用AAS得到三角形ABE与三角形ADF全等,利用全等三角形的对应边相等得到AE=AF,可得出AECF为正方形,三角形ABE面积与三角形AFD面积相等,进而得到四边形ABCD面积等于正方形AECF面积,求出正方形的边长即为AE的长,在等腰直角三角形ACE中,利用勾股定理即可求出AC的长.
【详解】解:过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F
∵∠AEC=∠AFC=∠ECF=90°,
∴四边形AECF为矩形,
∴∠EAF=90°,
∵∠BAD=90°,
∴∠BAE+∠EAD=∠FAD+∠EAD=90°,
∴∠DAF=∠BAE,
在△ABE和△ADF中,
∴△ABE≌△ADF(AAS),
∴AE=AF,S△ABE=S△ADF,
∴四边形AECF是正方形,
∴S四边形ABCD=S正方形AECF=24cm2,
∴AE=2cm,
∵△AEC为等腰直角三角形,
∴AC=AE=4cm.
故答案为:4.
【点睛】此题考查了全等三角形的判定与性质,矩形的判定与性质,正方形的判定与性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.
18.(1)矩形,正方形(任写一种即可);(2)详见解析
【分析】(1)直接利用勾股四边形的定义得出答案;
(2)根据要求分别得出符合题意的图形.
【详解】(1)矩形,正方形(任写一种即可);
(2)
【点睛】此题主要考查了轴对称变换,正确把握定义是解题关键.
19.由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【分析】根据旋转的性质可得出旋转方法.
【详解】解:图中可以将看作基本图案,图中的风车可以由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【点睛】此题主要考查了旋转的性质以及利用旋转设计图案,根据已知图形利用旋转性质得出是解题关键.
20.(1)见解析;(2)见解析
【分析】(1)直接利用轴对称图形的性质分析得出答案;
(2)直接利用中心对称图形的性质分析得出答案.
【详解】解:(1)如图所示:(答案不唯一);
(2)如图所示:(答案不唯一).
【点睛】此题主要考查了利用旋转设计图案以及轴对称变换,正确掌握相关定义是解题关键.
21.(1)见解析
(2)见解析
【分析】(1)根据要求作出图形即可;
(2)根据自己的喜好判断即可.
【详解】(1)解:如图所示,
(2)我更喜欢图3,理由:它既是轴对称图形,也是中心对称图形(答案不唯一).
【点睛】本题考查图案设计,中心对称图形,轴对称图形等知识,解题的关键是理解中心对称图形,轴对称图形的定义,属于中考常考题型.
22.由一个直角三角形绕正方形中心连续三次顺(或逆)时针旋转90°得到的
【分析】如图所示,基本图形为直角三角形ABC,然后根据图形的特点即可得到旋转方式.
【详解】解:如图所示,图案是直角三角形ABC绕点O(正方形的中线)顺时针(或逆时针)旋转三次,每次旋转90°得到的.
【点睛】本题主要考查了利用旋转设计图案,仔细观察图形找出旋转点以及基本图形是关键.
23.(1)图形见解析;
(2)图形见解析
【分析】(1)利用中心对称图形和轴对称图形的性质画出符合题意的图形即可;
(2)利用中心对称图形和轴对称图形的性质画出符合题意的图形即可.
【详解】(1)解:如图①,作点B关于直线的对称点D,
四边形即为所求作;
(2)解:如图②,四边形即为所求作.
【点睛】本题考查了利用旋转设计图案以及利用轴对称设计图案,正确把握中心对称和轴对称图形的定义是解题关键.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
24.图见解析
【分析】轴对称图形是指在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;中心对称图形是指在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【详解】解:如图所示:图2既是轴对称图形,又是中心对称图形;图3是轴对称图形,但不是中心对称图形;图4是中心对称图形,但不是轴对称图形.
【点睛】本题考查了中心对称图形和轴对称图形的概念,注意两个概念的区别.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4简单的图案设计
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面的图形能拼成正方形的是( ).
A. B. C.
2.下列图形中不是由平移设计的是( )
A. B. C. D.
3.给出下列图形:(1)角;(2)直角三角形;(3)等腰三角形;(4)平行四边形;(5)圆.其中为中心对称图形的是( )
A.(4)(5) B.(2)(3)(5) C.(3)(4) D.(1)(3)(4)(5)
4.“小小竹排水中游,巍巍青山两岸走”所描绘的图形变换主要是 ( )
A.平移变换 B.旋转变换 C.轴对称变换 D.中心对称
5.如图,图案(1)变成图案(2)是由下列哪种变换而成的( )
A.平移变换 B.轴对称变换 C.旋转变换 D.相似变换
6.下列四张扑克牌中,属于中心对称图形的是 ( )
A.红桃7 B.方块4 C.梅花6 D.黑桃5
7.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
8.我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是中心对称图形的是( )
A.①③ B.①④ C.②③ D.②④
9.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.2种 B.3种 C.4种 D.5种
10.下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是 ( )
A. B.
C. D.
11.由图中三角形仅经过一次平移、旋转或轴对称变换,不能得到的图形是( )
A. B. C. D.
12.下列图案中,可以看成由某一个基本图形通过平移形成的是( )
A. B. C. D.
二、填空题
13.如图, 在平面直角坐标系xOy中, △OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程 .
14.如图,可以看作是一个基础图形绕着中心旋转次而生成的,则每次旋转的度数是 .
15.如图,将左边的图案变成右边的图案的操作是 .
16.如图所示,在中,,将绕点顺时针旋转60°得到,与交于点,则 °,直线与所夹锐角的度数为 .
17.如图,四边形ABCD中,∠BAD=∠BCD=900,AB=AD,若四边形ABCD的面积是24cm2.则AC长是 cm.
三、解答题
18.阅读与探究
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:
在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可);
图1、图2均为的正方形网格,点均在格点上,请在图中标出格点,连接,使得四边形符合下列要求:图1中的四边形是勾股四边形,并且是轴对称图形;图2中的四边形是勾股四边形且对角线相等,但不是轴对称图形.
19.图中的风车图案,可以由哪个基本的图形、经过什么样的旋转得到?
20.图1,图2都是由边长为1的小正方形构成的网格,的三个顶点都在格点上,请在该的网格中,分别按下列要求画一个与有公共边的三角形:
(1)使得所画出的三角形和组成一个轴对称图形.
(2)使得所画出的三角形和组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
21.在的方格内选5个小正方形.
(1)在图1中,让它们以虚线为对称轴,组成一个轴对称图形;在图2中,让它们以虚线为对称轴组成一个轴对称图形;在图3中,让它们构成一个中心对称图形.请在图中画出你的这3种方案.(每个的方格内限画一种)
要求:①5个小正方形必须相连在一起(有公共边或公共顶点视为相连);②将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形能够重合,视为一种方案)
(2)在你所画得三个图中,最喜欢的是哪一个?简要说明理由.
22.如图,下面的图案是由什么基本图案经怎样的旋转得到的?
23.图①、图②均为的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以点A,B,C,D为顶点的四边形,使其为轴对称图形,但不是中心对称图形(画一个即可);
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
24.用四块如图1所示的正方形瓷砖拼成一个新的正方形,请你在图2,、图3、图4中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
《3.4简单的图案设计》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A A C B B D A D
题号 11 12
答案 B C
1.C
【分析】根据正方形的特点可知,两个直角边不相等的直角三角形不能拼成正方形;两个完全一样的正方形不能拼成正方形;选项C的图形可以拼成正方形.据此选择.
【详解】能拼成正方形的是:
故选:C.
【点睛】本题主要考查图形的拼组,关键掌握正方形的特征.
2.D
【分析】根据平移设计图案的定义即可依次判断.
【详解】A、B、C均是平移设计,D为旋转设计,
故选D.
【点睛】此题主要考查平移设计图案,解题的关键是熟知平移设计图案的特点.
3.A
【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;根据中心对称图形的定义,可得角旋转后无法与原角重合,即可进行判断,同理,即可判断其它各项是否为中心对称图形.
【详解】角不是中心对称图形,故(1)不是中心对称图形;
直角三角形不一定是中心对称图形,故(2)不一定是中心对称图形;
等腰三角形不一定是中心对称图形,故(3)不一定是中心对称图形;
平行四边形是中心对称图形,故(4)是中心对称图形;
圆是中心对称图形,故(5)是中心对称图形.
故是中心对称图形的是(4)(5).
故选A.
【点睛】此题考查中心对称图形的性质,解题关键在于掌握其性质.
4.A
【分析】根据诗歌知是小舟在水中行走,故为平移变换.
【详解】根据诗歌知是小舟在水中行走,故为平移变换,故选A.
【点睛】此题主要考查图形变换的类型.
5.C
【分析】图案旋转变换具备三个要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
【详解】根据观察可知,图案(1)变成图案(2)是由旋转变换而成的.
故选 C.
【点睛】本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
6.B
【详解】A选项:红桃7不是中心对称的图形;
B选项:方块4是中心对称的图形;
C选项:梅花6不是中心对称的图形;
D选项:黑桃5不是中心对称的图形;
故选B.
【点睛】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
7.B
【分析】根据题中所给剪纸方法,进行手动操作,答案就能很直观的呈现.
【详解】按照图中顺序进行操作,展开后心形图案应该靠近正方形上下两边,且关于中间折线对称,故只有B选项符合.
故选B.
【点睛】本题考查剪纸问题,解决此类问题要熟知轴对称图形的特点,关键是准确的找到对称轴,一般的方法是动手操作,拿张纸按照题中的要求进行操作.
8.D
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.
【详解】解:①不是中心对称图形,故本选项不合题意;
②是中心对称图形,故本选项符合题意;
③不是中心对称图形,故本选项不合题意;
④是中心对称图形,故本选项符合题意;
故选:D.
【点睛】本题考查了中心对称图形的定义,熟悉掌握概念是解题的关键
9.A
【详解】试题解析:如图,
有2种方法.
故选A.
10.D
【详解】试题分析:根据旋转的性质以及轴对称变换性质分别分析得出即可.
解:A、无法借助旋转得到,故此选项错误;
B、无法借助旋转得到,故此选项错误;
C、可以借助轴对称得到,故此选项错误;
D、可以只经过一次旋转运动即可和另一个三角形,故此选项正确.
故选D.
点评:此题主要考查了利用旋转设计图案,掌握旋转的性质是解题关键.
11.B
【详解】试题分析:根据平移、旋转和轴对称的性质即可得出正确结果.
解:A、经过平移可得到上图,故选项错误;
B、经过平移、旋转或轴对称变换后,都不能得到上图,故选项正确;
C、经过轴对称变换可得到上图,故选项错误;
D、经过旋转可得到上图,故选项错误.
故选B.
点评:本题考查了几何变换的类型,平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是沿某条直线翻折得到新图形.观察时要紧扣图形变换特点,进行分析判断.
12.C
【分析】本题考查了利用平移设计图案,确定一个基本图案,按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案,进而可得答案.
【详解】解:A、不能看成由某一个基本图形通过平移形成的,故不符合题意;
B、不能看成由某一个基本图形通过平移形成的,故不符合题意;
C、能看成由某一个基本图形通过平移形成的,故符合题意;
D、不能看成由某一个基本图形通过平移形成的,故不符合题意;
故选:C.
13.将△AOB顺时针旋转90°,再向左平移2个单位长度
【分析】根据平移、旋转的性质即可得到由△AOB得到△OCD的过程.
【详解】解:将△AOB顺时针旋转90°,再向左平移2个单位长度得到△OCD,
故答案为:将△AOB顺时针旋转90°,再向左平移2个单位长度.
【点睛】本题考查了坐标与图形变化-旋转,坐标与图形变化-平移,解题时需要注意:平移的距离等于对应点连线的长度.
14.
【详解】试题分析:∵一个周角是360度,等腰直角三角形的一个锐角是45度,
∴如图,是由一个等腰直角三角形每次旋转45度,且旋转8次形成的.
∴每次旋转的度数是45°.
故答案是45°.
考点:旋转的性质.
15.旋转
【分析】根据图形旋转的性质即可得出结论.
【详解】解:将左边的图案绕图案中的长方形中心逆时针旋转即可得到右边的图案.
故答案为:旋转.
【点睛】本题考查的是几何变换的类型,熟知图形旋转的性质是解答此题的关键.
16. 90 60°
【分析】先根据旋转的性质得∠CAE=60°,再利用三角形内角和定理计算出∠AFC=90°,延长CB交DE于G,在中即可求得∠EGF=60°.
【详解】∵△ABC绕点A顺时针旋转60°得△ADE,且∠C=30°,
∴∠CAE=60°,∠AED=∠C =30°,
在中,,
∴∠AFB=;
延长CB交DE于G,
在中,∠AED=∠C =30,∠EFG= =,
∴,
∴直线与所夹锐角的度数为,
故答案为:,.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
17.4
【分析】过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,利用三个角为直角的四边形为矩形得到AECF为矩形,利用矩形得四个角为直角得到∠EAF为直角,利用等式的性质得到∠DAF=∠BAE,再由一对直角相等,AB=AD,利用AAS得到三角形ABE与三角形ADF全等,利用全等三角形的对应边相等得到AE=AF,可得出AECF为正方形,三角形ABE面积与三角形AFD面积相等,进而得到四边形ABCD面积等于正方形AECF面积,求出正方形的边长即为AE的长,在等腰直角三角形ACE中,利用勾股定理即可求出AC的长.
【详解】解:过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F
∵∠AEC=∠AFC=∠ECF=90°,
∴四边形AECF为矩形,
∴∠EAF=90°,
∵∠BAD=90°,
∴∠BAE+∠EAD=∠FAD+∠EAD=90°,
∴∠DAF=∠BAE,
在△ABE和△ADF中,
∴△ABE≌△ADF(AAS),
∴AE=AF,S△ABE=S△ADF,
∴四边形AECF是正方形,
∴S四边形ABCD=S正方形AECF=24cm2,
∴AE=2cm,
∵△AEC为等腰直角三角形,
∴AC=AE=4cm.
故答案为:4.
【点睛】此题考查了全等三角形的判定与性质,矩形的判定与性质,正方形的判定与性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.
18.(1)矩形,正方形(任写一种即可);(2)详见解析
【分析】(1)直接利用勾股四边形的定义得出答案;
(2)根据要求分别得出符合题意的图形.
【详解】(1)矩形,正方形(任写一种即可);
(2)
【点睛】此题主要考查了轴对称变换,正确把握定义是解题关键.
19.由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【分析】根据旋转的性质可得出旋转方法.
【详解】解:图中可以将看作基本图案,图中的风车可以由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【点睛】此题主要考查了旋转的性质以及利用旋转设计图案,根据已知图形利用旋转性质得出是解题关键.
20.(1)见解析;(2)见解析
【分析】(1)直接利用轴对称图形的性质分析得出答案;
(2)直接利用中心对称图形的性质分析得出答案.
【详解】解:(1)如图所示:(答案不唯一);
(2)如图所示:(答案不唯一).
【点睛】此题主要考查了利用旋转设计图案以及轴对称变换,正确掌握相关定义是解题关键.
21.(1)见解析
(2)见解析
【分析】(1)根据要求作出图形即可;
(2)根据自己的喜好判断即可.
【详解】(1)解:如图所示,
(2)我更喜欢图3,理由:它既是轴对称图形,也是中心对称图形(答案不唯一).
【点睛】本题考查图案设计,中心对称图形,轴对称图形等知识,解题的关键是理解中心对称图形,轴对称图形的定义,属于中考常考题型.
22.由一个直角三角形绕正方形中心连续三次顺(或逆)时针旋转90°得到的
【分析】如图所示,基本图形为直角三角形ABC,然后根据图形的特点即可得到旋转方式.
【详解】解:如图所示,图案是直角三角形ABC绕点O(正方形的中线)顺时针(或逆时针)旋转三次,每次旋转90°得到的.
【点睛】本题主要考查了利用旋转设计图案,仔细观察图形找出旋转点以及基本图形是关键.
23.(1)图形见解析;
(2)图形见解析
【分析】(1)利用中心对称图形和轴对称图形的性质画出符合题意的图形即可;
(2)利用中心对称图形和轴对称图形的性质画出符合题意的图形即可.
【详解】(1)解:如图①,作点B关于直线的对称点D,
四边形即为所求作;
(2)解:如图②,四边形即为所求作.
【点睛】本题考查了利用旋转设计图案以及利用轴对称设计图案,正确把握中心对称和轴对称图形的定义是解题关键.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
24.图见解析
【分析】轴对称图形是指在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;中心对称图形是指在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【详解】解:如图所示:图2既是轴对称图形,又是中心对称图形;图3是轴对称图形,但不是中心对称图形;图4是中心对称图形,但不是轴对称图形.
【点睛】本题考查了中心对称图形和轴对称图形的概念,注意两个概念的区别.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
