3.2图形的旋转随堂练习 北师大版数学八年级下册(含解析)
文档属性
| 名称 | 3.2图形的旋转随堂练习 北师大版数学八年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:33:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.2图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将数字“6”旋转,得到数字“9”;将数字“9”旋转,得到的数字是“6”,现将数字“69”旋转,得到的数字是( )
A.96 B.69 C.66 D.99
2.如图,在△EBC中,∠E=∠ECB=60°,EC=BC=5,点O在BC上,且OC=3,动点P从点E沿射线EC以每秒1个单位长度的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF要使点F恰好落在射线EB上,求点P运动的时间t为( )秒
A.7 B.7或4 C.4或5 D.4
3.如图, 将 绕点顺时针旋转一定的角度与 重合 与 是对应点 , 使得点恰好落在上, 若, 则 的度数为 ( )
A. B. C. D.
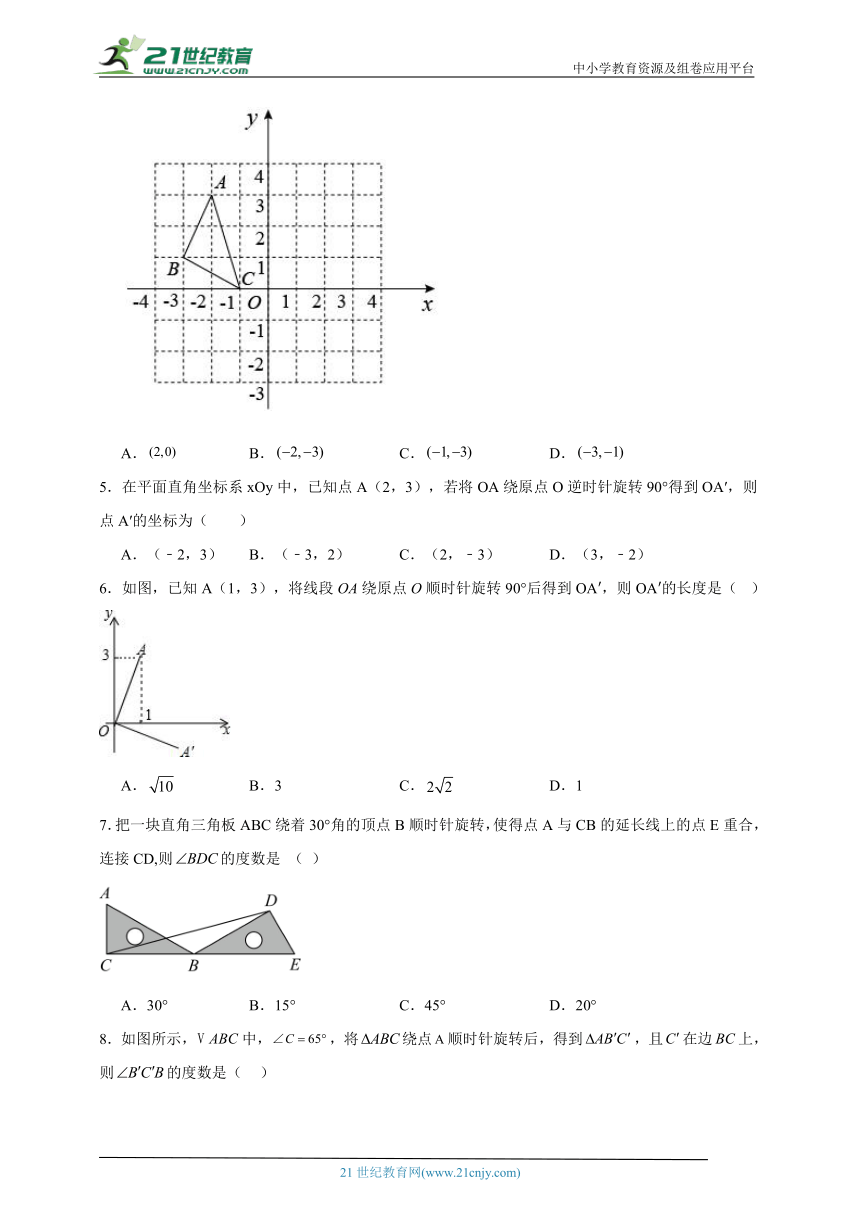
4.如图,将先向右平移3个单位,再绕原点O旋转,得到,则点A的对应点的坐标是( )
A. B. C. D.
5.在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标为( )
A.(﹣2,3) B.(﹣3,2) C.(2,﹣3) D.(3,﹣2)
6.如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
A. B.3 C. D.1
7.把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则的度数是 ( )
A.30° B.15° C.45° D.20°
8.如图所示,中,,将绕点顺时针旋转后,得到,且在边上,则的度数是( )
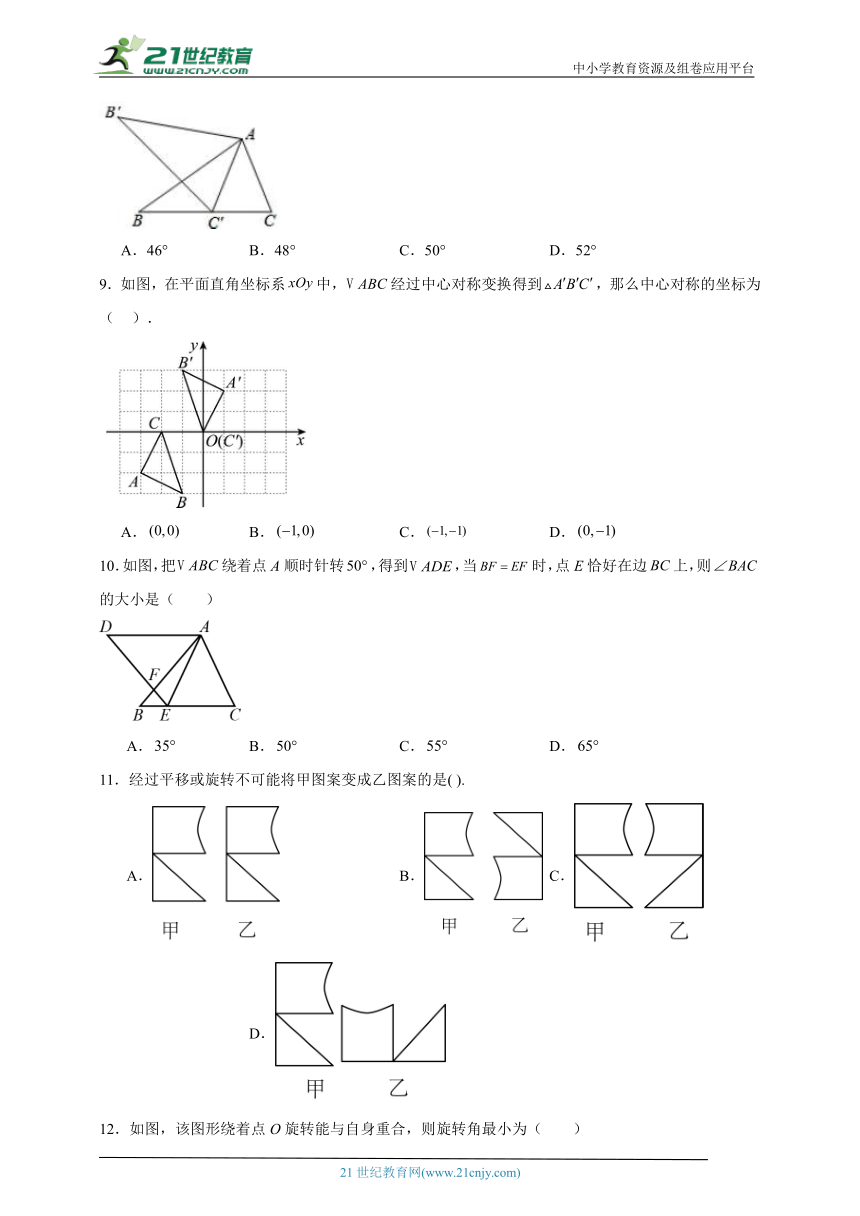
A.46° B.48° C.50° D.52°
9.如图,在平面直角坐标系中,经过中心对称变换得到,那么中心对称的坐标为( ).
A. B. C. D.
10.如图,把绕着点A顺时针转,得到,当时,点E恰好在边上,则的大小是( )
A. B. C. D.
11.经过平移或旋转不可能将甲图案变成乙图案的是( ).
A. B. C. D.
12.如图,该图形绕着点O旋转能与自身重合,则旋转角最小为( )
A.36° B.60° C.72° D.90°
二、填空题
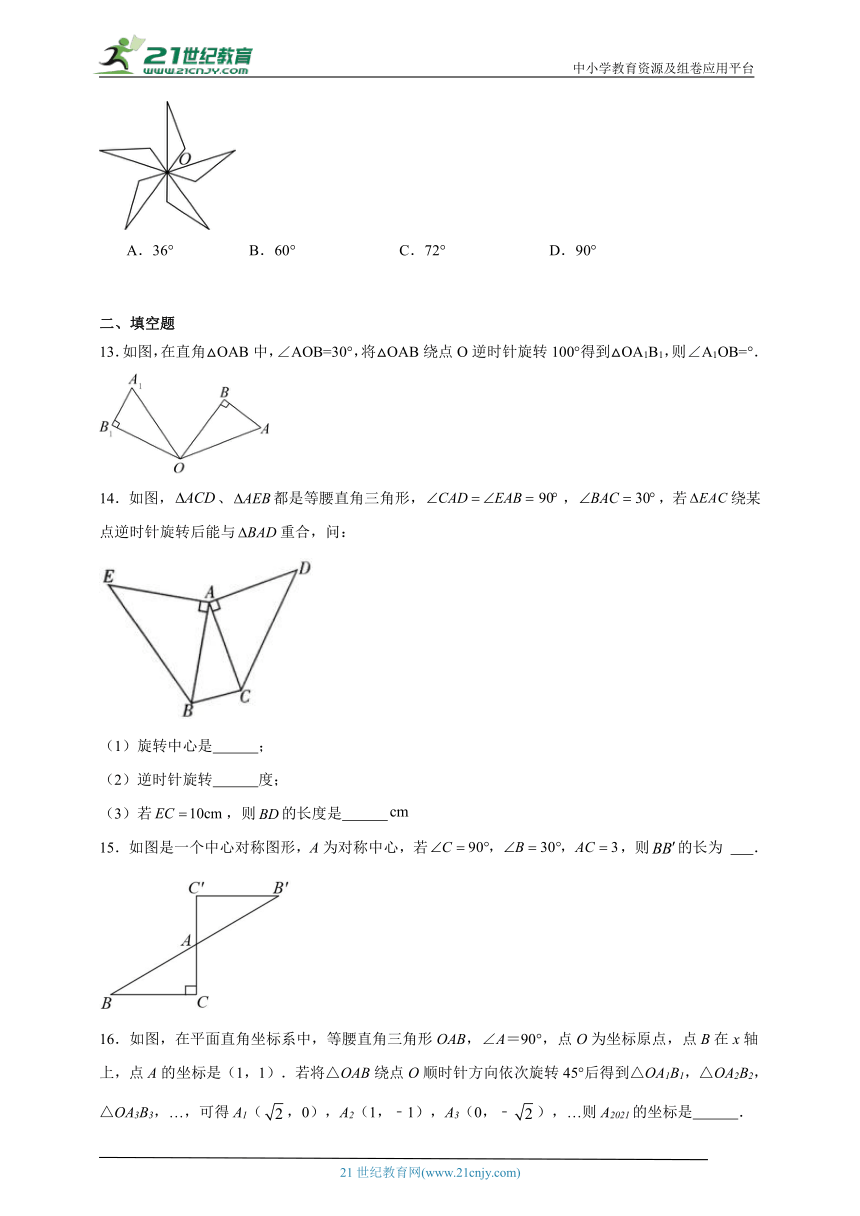
13.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB=°.
14.如图,、都是等腰直角三角形,,,若绕某点逆时针旋转后能与重合,问:
(1)旋转中心是 ;
(2)逆时针旋转 度;
(3)若,则的长度是
15.如图是一个中心对称图形,A为对称中心,若,则的长为 .
16.如图,在平面直角坐标系中,等腰直角三角形OAB,∠A=90°,点O为坐标原点,点B在x轴上,点A的坐标是(1,1).若将△OAB绕点O顺时针方向依次旋转45°后得到△OA1B1,△OA2B2,△OA3B3,…,可得A1(,0),A2(1,﹣1),A3(0,﹣),…则A2021的坐标是 .
17.如图,可以看作是一个基础图形绕着中心旋转次而生成的,则每次旋转的度数是 .
三、解答题
18.点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处.
(1)如图1,将三角板的一边与射线重合时,求的度数;
(2)如图2,将三角板绕点逆时针旋转一定角度,此时是的角平分线,求旋转角的度数,的度数;
(3)将三角板绕点逆时针旋转至图3时,,求.
19.如图,在由边长为1个单位的小正方形组成的网格中,的顶点都在格点(网格线的交点)上.
(1)将向下平移4个单位,再向右平移3个单位,得到,请画出;
(2)以边的中点O为旋转中心,将逆时针旋转,得到,请画出.
20.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出△ABC绕点O顺时针旋转90°后的△A′B′C′.
(2)求点B绕点O旋转到点B′的路径长(结果保留π).
21.如图1,在平面直角坐标系中,已知A(a,-a),B (b,0),且a,b满足
(1)判断△AOB的形状,并说明理由;
(2)如图1,E,F在OB边上,且E(—3,0),∠EAF=45°,求EF的长;
(3)如图2,若C(3,0),在y轴负半轴上是否存在点M,使∠FMO=2∠CMO,若存在,求点M的坐标,若不存在,请说明理由.
22.如图1,点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点逆时针旋转至图2,使一边在的内部,且恰好平分,问:直线是否平分?请直接写出结论:直线 (平分或不平分).
(2)将图1中的三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线恰好平分锐角,则的值为 .(直接写出结果)
(3)将图1中的三角板绕点O顺时针旋转,请探究,当始终在的内部时(如图3),与的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
23.(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
24.如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C 的坐标分别为A(-3,5)、C(0,3)
备用图
(1)请在网格所在的平面内画出平面直角坐标系,并直接写出点B的坐标
(2)将△ABC绕着原点O顺时针旋转90°得△A1B1C1,画出△A1B1C1
(3)在x轴上是否存在点P,使PA+PC的值最小,若存在请直接写出点P的坐标;若不存在请说明理由
《3.2图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C B A B C B D
题号 11 12
答案 C C
1.B
【分析】直接旋转的性质结合69的特点得出答案.
【详解】解:现将数字“69”旋转,得到的数字是:69,
故选:B.
【点睛】本题主要考查了旋转的性质,熟练掌握旋转的性质,得出旋转后的图形是解题关键.
2.A
【分析】利用旋转的性质得∠FOP=120°,OP=OF,再证明△BOF≌△CPO得到PC=OB=1,则BP=BC+PC=4,然后计算点P运动的时间t.
【详解】解:如图,∵OC=3,
∴OB=BC-OC=2,
∵线段OP绕点O逆时针旋转120°得到线段OF,
∴∠FOP=120°,OP=OF,
∴∠1+∠2=60°,
∵△BCE为等边三角形,
∴∠BCE=∠CBE=60°,
∴∠FBO=120°,∠PCO=120°,
∴∠2+∠3=∠BCE=60°,
∴∠1=∠3,
∴△BOF≌△CPO(AAS),
∴PC=OB=2,
∴EP=EC+PC=BC+PC=5+2=7,
∴点P运动的时间t=7÷1=7s,
故选A.
【点睛】本题是几何变换综合题,主要考查了旋转的性质和等边三角形的性质,会运用全等三角形的知识解决线段相等的问题;判断出△BOF≌△CPO是解本题的关键.
3.B
【分析】由旋转的性质可得:AC=AC',∠ACB=∠AC'B'=75°,可求∠ACB'=105°,即可得∠BCB′的度数.
【详解】解:∵将△ABC绕点A顺时针旋转一定的角度至△AB′C′处,
∴AC=AC',∠ACB=∠AC'B'=75°,
∴∠ACC'=∠AC'B'=75°,
∴∠ACB'=105°,
∵∠BCB'=∠ACB'-∠ACB=105°-75°=30°,
故选:B.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
4.C
【分析】先画出平移后的图形,再利用旋转的性质画出旋转后的图形即可求解.
【详解】解:先画出△ABC平移后的△DEF,再利用旋转得到△A'B'C',
由图像可知A'(-1,-3),
故选:C.
【点睛】本题考查了图形的平移和旋转,解题关键是掌握绕原点旋转的图形的坐标特点,即对应点的横纵坐标都互为相反数.
5.B
【详解】试题分析:作出图形,然后写出点A′的坐标即可.
如图,点A′的坐标为(﹣3,2).
故选B.
考点: 坐标与图形变化-旋转.
6.A
【详解】试题解析:∵A点坐标为(1,3),
∴OA==,
∵线段OA绕原点O顺时针旋转90°后得到OA′,
∴OA′=OA=.
故选A.
点睛:旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
7.B
【详解】试题分析:∵把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,
∴BC=BD,∠DBE=∠ABC=30°,
∴∠BDC=15°
故选B
考点:等腰三角形的性质
8.C
【分析】根据旋转的性质和∠C=65°,从而可以求得∠AC′B′和∠AC′C的度数,从而可以求得∠B′C′B的度数.
【详解】∵将△ABC绕点A顺时针旋转后,可以得到△AB′C′,且C′在边BC上,
∴AC=AC′,∠C=∠AC′B′,
∴∠C=∠AC′C,
∵∠C=65°,
∴∠AC′B′=65°,∠AC′C=65°,
∴∠B′C′B=180° ∠AC′B′ ∠AC′C=50°,
故选:C.
【点睛】本题考查旋转的性质,解题的关键是明确题意,找出所求问题需要的条件.
9.B
【详解】如图,连接可得它们的交点坐标为,
∵成中心对称的两个图形中,对应点的连线必过对称中心,
∴对称中心的坐标为:,
故选B.
10.D
【分析】根据旋转的性质得出,,进而利用三角形内角和定理解答即可.
【详解】解:把绕着点A顺时针转,得到,
∴,
∴,
∴,
∴,
∵.
∴,
∵,
∴,
故选:D.
【点睛】此题考查旋转的性质和三角形内角和定理,关键是根据旋转的性质求旋转角.
11.C
【详解】本题考查了平移和旋转的性质
根据平移和旋转的性质进行选择,平移不改变图形的大小和形状,旋转改变图形的方向,可以作出选择.
A、B、D通过旋转和平移,和乙图各点对应,均正确;C、经过平移和旋转变换不可能将甲图案变成乙,故错误.故选C.
12.C
【分析】根据旋转对称图形的性质判断即可.
【详解】解:由题意,=72°,
故该图形围绕点O旋转能与自身重合,则旋转角最小为72°,
故选:C.
【点睛】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
13.70
【详解】∵将△OAB绕点O逆时针旋转100°得到△OA1B1, ∴∠A1OA=100°.
又∵∠AOB=30°,∴∠A1OB=∠A1OA-∠AOB=70°.
14. 点 90 10
【分析】(1)找出两重合三角形的公共顶点即可得出其旋转中心;
(2)根据两重合边所夹的角度即可求出旋转的度数;
(3)根据图形旋转的性质可直接进行解答.
【详解】(1)∵△EAC逆时针旋转后能与△BAD重合,
∴A点即为两三角形的公共顶点,故旋转中心是A点;
(2)∵△EAC逆时针旋转后能与△BAD,
∴AE与AB重合,
∵∠BAE=90°,
∴旋转的度数为:90;
(3)由题意知EC和BD是对应线段,据旋转的性质可得BD=EC=10cm.
【点睛】本题考查的是图形旋转的性质,即①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.
15.12
【分析】先根据含30度角的直角三角形的性质得到,再根据中心对称图形的性质即可得到答案.
【详解】解:∵在中,,
∴,
∵B与关于A中心对称,
∴.
故答案为:12.
【点睛】本题主要考查了中心对称图形的性质,含30度角的直角三角形的性质,正确求出是解题的关键.
16.
【分析】根据题意得:A1(,0),A2(1,﹣1),A3(0,﹣), ,…,由此发现,旋转8次一个循环,再由 ,即可求解.
【详解】解:根据题意得:A1(,0),A2(1,﹣1),A3(0,﹣), ,…,由此发现,旋转8次一个循环,
∵ ,
∴A2021的坐标是 .
故答案为:
【点睛】本题主要考查了图形的旋转,明确题意,准确得到规律是解题的关键.
17.
【详解】试题分析:∵一个周角是360度,等腰直角三角形的一个锐角是45度,
∴如图,是由一个等腰直角三角形每次旋转45度,且旋转8次形成的.
∴每次旋转的度数是45°.
故答案是45°.
考点:旋转的性质.
18.(1)25° (2)40°,25° (3)20°.
【分析】(1)直接利用角的和差计算即可;
(2)先根据角平分线的性质求得∠MOB=130°,再根据旋转角的定义,然后∠BOC-∠BON即可求得;
(3)先求出∠BON,然后利用平角的性质和角的和差即可解答.
【详解】(1),
故答案为25°;
(2)∵是的角平分线,
∴,
∴旋转角,
,
故答案为40°,25°;
(3)∵,,
∴,
∵点为直线上一点,
∴,
∵,
∴.
【点睛】本题主要考查了角平分线的定义、旋转角的性质、直角的性质和角的和差等知识点,考查知识点较多,灵活运用所学知识成为解答本题的关键.
19.(1)见解析
(2)见解析
【分析】(1)根据平移的性质作图:分别作出点A、B、C向下平移4个单位,再向右平移3个单位的对应点,,,再连接,,即可.
(2)根据旋转的性质作图:分别作出点A、B、C绕点O逆时针旋转90°的对应点D,E,F,再连接,,,即可.
【详解】(1)解:如图,即为所求.
(2)解:如图,即为所求.
【点睛】本题考查作图-平移变换、旋转变换,熟练掌握平移和旋转的性质是解答本题的关键.
20.(1)画图见解析;(2)点B绕点O旋转到点B′的路径长为.
【分析】(1)利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′,从而得到△A′B′C′;
(2)先计算出OB的长,然后根据弧长公式计算点B绕点O旋转到点B′的路径长.
【详解】(1)如图,△A′B′C′为所作;
(2)OB==3,点B绕点O旋转到点B′的路径长==π.
【点睛】本题考查作图﹣旋转变换和旋转的性质,解题的关键是掌握旋转的性质.
21.(1)△AOB 为等腰直角三角形,理由见解析;
(2)EF的长为5;
(3)存在,M点坐标为(0,-6),理由见解析.
【分析】(1)利用,可知a,b的值,从而知道点A、B的坐标,继而推导出△OAH与△BAH是两个全等的等腰直角三角形,最后得出△AOB 为等腰直角三角形;
(2)将△AOE绕A点顺时针旋转90°得到△ABG,从而构造Rt △FBG,再用SAS证明△GAF≌△EAF(SAS),从而得到,最后设EF为x,构造方程解出即可;
(3)取取点C(3,0)关于y轴对称的对称点P(-3,0),利用∠FMO=2∠CMO得到PM是∠FMO 的角平分线,再用等面积法得出,再设OM=3t,利用勾股定理构造方程,解出方程推出M点坐标.
【详解】(1)△AOB 为等腰直角三角形,理由如下:
过点 A 作 AH⊥OB, 垂足为 H,
∵,
∴,
又∵A(a,),B (b,0),
∴,B,
∴OH= HB =AH=6.
又∵AH⊥OB,
∴△OAH与△BAH是两个全等的等腰直角三角形(SAS),
∴∠ABO=∠AOB=45°,AB=AO,∠BAO=∠BAH+∠OAH=45°+45°= 90°.
∴△AOB 为等腰直角三角形.
(2)将△AOE绕A点顺时针旋转90°得到△ABG,旋转后AO与AB重合,
则有∠ABG=∠AOE=45°,BG=OE,AG=AE,∠BAG=∠OAE,
∠FBG=∠ABO+∠ABG=45°+45°=90°,
.
又∵∠BAO= 90°,∠EAF=45°,
∴∠GAF=∠BAG+∠BAF=∠OAE +∠BAF=∠BAO-∠EAF=,
∴∠GAF=∠EAF.
∵AG=AE,∠GAF=∠EAF ,AF=AF,
∴△GAF≌△EAF(SAS),
∴FG=EF.
∵,
∴OE=3.
∵,FG=EF,BG=OE,
∴.
设EF=x,则BF=OB-OE-x=9-x,
∴,
解得:x=5,即EF的长为5.
(3)存在,M点坐标为,理由如下:
取点C(3,0)关于y轴对称的对称点P(-3,0),
由(2)知OF=EF+OE=8,
∴.
连接 MP, 过点 P 作 PK⊥MF, 垂足为 K,
∵OP=OC=3,
∴MO 垂直平分 CP,
∴MP=MC,∠CMO=∠PMO.
∵∠FMO=2∠CMO,
∴∠FMO=2∠PMO ,
∴,
∴PM是∠FMO 的角平分线.
又∵PK⊥MF,PO⊥OM,
∴PK=PO,
∴.
又∵,
∴.
设 MF=5t, 则 MO=3t,
∵,
∴,
∴(含去),
∴,MO=3t=6,
∴M 点的坐标为.
【点睛】本题考查等腰直角三角形的判定与性质,旋转的性质,等面积法,方程思想解决几何问题等知识,第二小问解题的关键是利用旋转构造直角三角形,第三小问解题的关键是等面积法推出与的比例关系.
22.(1)平分
(2)或
(3)不变,差值是
【分析】(1)设的反向延长线为,由角平分线的性质和对顶角的性质可求得;
(2)由直线恰好平分锐角可知旋转或时直线平分,根据旋转速度可求得需要的时间;
(3)由,可知,最后求得两角的差,从而可做出判断.
【详解】(1)解:直线平分.
理由如下:设的反向延长线为,
∵平分,
∴,
又,
∴,
∵,
∴,∴平分,
即直线平分,故答案为:平分;
(2)∵,∴.
∴.
即旋转或时直线ON平分∠AOC.
由题意得,或.
解得:或,
故答案为:或;
(3)的差不变.
∵,
∴,
∴.
∴与的差不变,这个差值是.
【点睛】本题考查了旋转的性质,角平分线的定义,几何图形中角度的计算,掌握旋转的性质,数形结合是解题的关键.
23.(1) AD=BE,AD⊥BE.(2) AD=BE,AD⊥BE.(3) 5-3≤PC≤5+3.
【分析】(1)根据等腰三角形性质证△ACD≌△BCE(SAS),得AD=BE,∠EBC=∠CAD,延长BE交AD于点F,由垂直定义得AD⊥BE.
(2)根据等腰三角形性质证△ACD≌△BCE(SAS),AD=BE,∠CAD=∠CBE,由垂直定义得∠OHB=90°,AD⊥BE;
(3)作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,PC=BE,当P、E、B共线时,BE最小,最小值=PB-PE;当P、E、B共线时,BE最大,最大值=PB+PE,故5-3≤BE≤5+3.
【详解】(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
故答案为AD=BE,AD⊥BE.
(2)结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-3,
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3,
∴5-3≤BE≤5+3,
即5-3≤PC≤5+3.
【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.
24.(1)作图如图所示,点B的坐标为(-2,1)
(2)作图如图所示
(3)存在点,使得PA+PC的值最小.
【分析】(1)根据A、C 的坐标确定平面直角坐标系的原点位置,从而画出平面直角坐标系,并得到点B的坐标
(2)根据旋转的定义作图即可
(3)根据图形对称性质,作点C关于x轴的对称点C2,连接A C2,则A C2交x轴于点P,此时PA+PC的值最小.此时由A(-3,5),C2(0,-3),求得直线A C2的解析式,进而求出直线A C2与x轴的交点,即得P点坐标.
【详解】(1)解:由A、C 的坐标分别为A(-3,5)、C(0,3),可得平面直角坐标系如图所示,点B的坐标为(-2,1).
(2)解:作图如图所示,
(3)解:存在点,使得PA+PC的值最小.
作点C关于x轴的对称点C2,连接A C2,则A C2交x轴于点P,此时PA+PC的值最小.
∵C(0,3),点C2为点C关于x轴的对称点,
∴C2(0,-3),
∵ A(-3,5),C2(0,-3),
设直线A C2的解析式为:,将A(-3,5),C2(0,-3)代入解析式中,
可得,,
解得,,
∴直线A C2的解析式为:,
令,得,
故存在,使得PA+PC的值最小.
【点睛】本题考查了平面直角坐标系,图形的旋转及对称性质,熟练掌握图形的旋转及对称变换是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将数字“6”旋转,得到数字“9”;将数字“9”旋转,得到的数字是“6”,现将数字“69”旋转,得到的数字是( )
A.96 B.69 C.66 D.99
2.如图,在△EBC中,∠E=∠ECB=60°,EC=BC=5,点O在BC上,且OC=3,动点P从点E沿射线EC以每秒1个单位长度的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF要使点F恰好落在射线EB上,求点P运动的时间t为( )秒
A.7 B.7或4 C.4或5 D.4
3.如图, 将 绕点顺时针旋转一定的角度与 重合 与 是对应点 , 使得点恰好落在上, 若, 则 的度数为 ( )
A. B. C. D.
4.如图,将先向右平移3个单位,再绕原点O旋转,得到,则点A的对应点的坐标是( )
A. B. C. D.
5.在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标为( )
A.(﹣2,3) B.(﹣3,2) C.(2,﹣3) D.(3,﹣2)
6.如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
A. B.3 C. D.1
7.把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则的度数是 ( )
A.30° B.15° C.45° D.20°
8.如图所示,中,,将绕点顺时针旋转后,得到,且在边上,则的度数是( )
A.46° B.48° C.50° D.52°
9.如图,在平面直角坐标系中,经过中心对称变换得到,那么中心对称的坐标为( ).
A. B. C. D.
10.如图,把绕着点A顺时针转,得到,当时,点E恰好在边上,则的大小是( )
A. B. C. D.
11.经过平移或旋转不可能将甲图案变成乙图案的是( ).
A. B. C. D.
12.如图,该图形绕着点O旋转能与自身重合,则旋转角最小为( )
A.36° B.60° C.72° D.90°
二、填空题
13.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB=°.
14.如图,、都是等腰直角三角形,,,若绕某点逆时针旋转后能与重合,问:
(1)旋转中心是 ;
(2)逆时针旋转 度;
(3)若,则的长度是
15.如图是一个中心对称图形,A为对称中心,若,则的长为 .
16.如图,在平面直角坐标系中,等腰直角三角形OAB,∠A=90°,点O为坐标原点,点B在x轴上,点A的坐标是(1,1).若将△OAB绕点O顺时针方向依次旋转45°后得到△OA1B1,△OA2B2,△OA3B3,…,可得A1(,0),A2(1,﹣1),A3(0,﹣),…则A2021的坐标是 .
17.如图,可以看作是一个基础图形绕着中心旋转次而生成的,则每次旋转的度数是 .
三、解答题
18.点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处.
(1)如图1,将三角板的一边与射线重合时,求的度数;
(2)如图2,将三角板绕点逆时针旋转一定角度,此时是的角平分线,求旋转角的度数,的度数;
(3)将三角板绕点逆时针旋转至图3时,,求.
19.如图,在由边长为1个单位的小正方形组成的网格中,的顶点都在格点(网格线的交点)上.
(1)将向下平移4个单位,再向右平移3个单位,得到,请画出;
(2)以边的中点O为旋转中心,将逆时针旋转,得到,请画出.
20.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出△ABC绕点O顺时针旋转90°后的△A′B′C′.
(2)求点B绕点O旋转到点B′的路径长(结果保留π).
21.如图1,在平面直角坐标系中,已知A(a,-a),B (b,0),且a,b满足
(1)判断△AOB的形状,并说明理由;
(2)如图1,E,F在OB边上,且E(—3,0),∠EAF=45°,求EF的长;
(3)如图2,若C(3,0),在y轴负半轴上是否存在点M,使∠FMO=2∠CMO,若存在,求点M的坐标,若不存在,请说明理由.
22.如图1,点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点逆时针旋转至图2,使一边在的内部,且恰好平分,问:直线是否平分?请直接写出结论:直线 (平分或不平分).
(2)将图1中的三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线恰好平分锐角,则的值为 .(直接写出结果)
(3)将图1中的三角板绕点O顺时针旋转,请探究,当始终在的内部时(如图3),与的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
23.(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
24.如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C 的坐标分别为A(-3,5)、C(0,3)
备用图
(1)请在网格所在的平面内画出平面直角坐标系,并直接写出点B的坐标
(2)将△ABC绕着原点O顺时针旋转90°得△A1B1C1,画出△A1B1C1
(3)在x轴上是否存在点P,使PA+PC的值最小,若存在请直接写出点P的坐标;若不存在请说明理由
《3.2图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C B A B C B D
题号 11 12
答案 C C
1.B
【分析】直接旋转的性质结合69的特点得出答案.
【详解】解:现将数字“69”旋转,得到的数字是:69,
故选:B.
【点睛】本题主要考查了旋转的性质,熟练掌握旋转的性质,得出旋转后的图形是解题关键.
2.A
【分析】利用旋转的性质得∠FOP=120°,OP=OF,再证明△BOF≌△CPO得到PC=OB=1,则BP=BC+PC=4,然后计算点P运动的时间t.
【详解】解:如图,∵OC=3,
∴OB=BC-OC=2,
∵线段OP绕点O逆时针旋转120°得到线段OF,
∴∠FOP=120°,OP=OF,
∴∠1+∠2=60°,
∵△BCE为等边三角形,
∴∠BCE=∠CBE=60°,
∴∠FBO=120°,∠PCO=120°,
∴∠2+∠3=∠BCE=60°,
∴∠1=∠3,
∴△BOF≌△CPO(AAS),
∴PC=OB=2,
∴EP=EC+PC=BC+PC=5+2=7,
∴点P运动的时间t=7÷1=7s,
故选A.
【点睛】本题是几何变换综合题,主要考查了旋转的性质和等边三角形的性质,会运用全等三角形的知识解决线段相等的问题;判断出△BOF≌△CPO是解本题的关键.
3.B
【分析】由旋转的性质可得:AC=AC',∠ACB=∠AC'B'=75°,可求∠ACB'=105°,即可得∠BCB′的度数.
【详解】解:∵将△ABC绕点A顺时针旋转一定的角度至△AB′C′处,
∴AC=AC',∠ACB=∠AC'B'=75°,
∴∠ACC'=∠AC'B'=75°,
∴∠ACB'=105°,
∵∠BCB'=∠ACB'-∠ACB=105°-75°=30°,
故选:B.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
4.C
【分析】先画出平移后的图形,再利用旋转的性质画出旋转后的图形即可求解.
【详解】解:先画出△ABC平移后的△DEF,再利用旋转得到△A'B'C',
由图像可知A'(-1,-3),
故选:C.
【点睛】本题考查了图形的平移和旋转,解题关键是掌握绕原点旋转的图形的坐标特点,即对应点的横纵坐标都互为相反数.
5.B
【详解】试题分析:作出图形,然后写出点A′的坐标即可.
如图,点A′的坐标为(﹣3,2).
故选B.
考点: 坐标与图形变化-旋转.
6.A
【详解】试题解析:∵A点坐标为(1,3),
∴OA==,
∵线段OA绕原点O顺时针旋转90°后得到OA′,
∴OA′=OA=.
故选A.
点睛:旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
7.B
【详解】试题分析:∵把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,
∴BC=BD,∠DBE=∠ABC=30°,
∴∠BDC=15°
故选B
考点:等腰三角形的性质
8.C
【分析】根据旋转的性质和∠C=65°,从而可以求得∠AC′B′和∠AC′C的度数,从而可以求得∠B′C′B的度数.
【详解】∵将△ABC绕点A顺时针旋转后,可以得到△AB′C′,且C′在边BC上,
∴AC=AC′,∠C=∠AC′B′,
∴∠C=∠AC′C,
∵∠C=65°,
∴∠AC′B′=65°,∠AC′C=65°,
∴∠B′C′B=180° ∠AC′B′ ∠AC′C=50°,
故选:C.
【点睛】本题考查旋转的性质,解题的关键是明确题意,找出所求问题需要的条件.
9.B
【详解】如图,连接可得它们的交点坐标为,
∵成中心对称的两个图形中,对应点的连线必过对称中心,
∴对称中心的坐标为:,
故选B.
10.D
【分析】根据旋转的性质得出,,进而利用三角形内角和定理解答即可.
【详解】解:把绕着点A顺时针转,得到,
∴,
∴,
∴,
∴,
∵.
∴,
∵,
∴,
故选:D.
【点睛】此题考查旋转的性质和三角形内角和定理,关键是根据旋转的性质求旋转角.
11.C
【详解】本题考查了平移和旋转的性质
根据平移和旋转的性质进行选择,平移不改变图形的大小和形状,旋转改变图形的方向,可以作出选择.
A、B、D通过旋转和平移,和乙图各点对应,均正确;C、经过平移和旋转变换不可能将甲图案变成乙,故错误.故选C.
12.C
【分析】根据旋转对称图形的性质判断即可.
【详解】解:由题意,=72°,
故该图形围绕点O旋转能与自身重合,则旋转角最小为72°,
故选:C.
【点睛】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
13.70
【详解】∵将△OAB绕点O逆时针旋转100°得到△OA1B1, ∴∠A1OA=100°.
又∵∠AOB=30°,∴∠A1OB=∠A1OA-∠AOB=70°.
14. 点 90 10
【分析】(1)找出两重合三角形的公共顶点即可得出其旋转中心;
(2)根据两重合边所夹的角度即可求出旋转的度数;
(3)根据图形旋转的性质可直接进行解答.
【详解】(1)∵△EAC逆时针旋转后能与△BAD重合,
∴A点即为两三角形的公共顶点,故旋转中心是A点;
(2)∵△EAC逆时针旋转后能与△BAD,
∴AE与AB重合,
∵∠BAE=90°,
∴旋转的度数为:90;
(3)由题意知EC和BD是对应线段,据旋转的性质可得BD=EC=10cm.
【点睛】本题考查的是图形旋转的性质,即①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.
15.12
【分析】先根据含30度角的直角三角形的性质得到,再根据中心对称图形的性质即可得到答案.
【详解】解:∵在中,,
∴,
∵B与关于A中心对称,
∴.
故答案为:12.
【点睛】本题主要考查了中心对称图形的性质,含30度角的直角三角形的性质,正确求出是解题的关键.
16.
【分析】根据题意得:A1(,0),A2(1,﹣1),A3(0,﹣), ,…,由此发现,旋转8次一个循环,再由 ,即可求解.
【详解】解:根据题意得:A1(,0),A2(1,﹣1),A3(0,﹣), ,…,由此发现,旋转8次一个循环,
∵ ,
∴A2021的坐标是 .
故答案为:
【点睛】本题主要考查了图形的旋转,明确题意,准确得到规律是解题的关键.
17.
【详解】试题分析:∵一个周角是360度,等腰直角三角形的一个锐角是45度,
∴如图,是由一个等腰直角三角形每次旋转45度,且旋转8次形成的.
∴每次旋转的度数是45°.
故答案是45°.
考点:旋转的性质.
18.(1)25° (2)40°,25° (3)20°.
【分析】(1)直接利用角的和差计算即可;
(2)先根据角平分线的性质求得∠MOB=130°,再根据旋转角的定义,然后∠BOC-∠BON即可求得;
(3)先求出∠BON,然后利用平角的性质和角的和差即可解答.
【详解】(1),
故答案为25°;
(2)∵是的角平分线,
∴,
∴旋转角,
,
故答案为40°,25°;
(3)∵,,
∴,
∵点为直线上一点,
∴,
∵,
∴.
【点睛】本题主要考查了角平分线的定义、旋转角的性质、直角的性质和角的和差等知识点,考查知识点较多,灵活运用所学知识成为解答本题的关键.
19.(1)见解析
(2)见解析
【分析】(1)根据平移的性质作图:分别作出点A、B、C向下平移4个单位,再向右平移3个单位的对应点,,,再连接,,即可.
(2)根据旋转的性质作图:分别作出点A、B、C绕点O逆时针旋转90°的对应点D,E,F,再连接,,,即可.
【详解】(1)解:如图,即为所求.
(2)解:如图,即为所求.
【点睛】本题考查作图-平移变换、旋转变换,熟练掌握平移和旋转的性质是解答本题的关键.
20.(1)画图见解析;(2)点B绕点O旋转到点B′的路径长为.
【分析】(1)利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′,从而得到△A′B′C′;
(2)先计算出OB的长,然后根据弧长公式计算点B绕点O旋转到点B′的路径长.
【详解】(1)如图,△A′B′C′为所作;
(2)OB==3,点B绕点O旋转到点B′的路径长==π.
【点睛】本题考查作图﹣旋转变换和旋转的性质,解题的关键是掌握旋转的性质.
21.(1)△AOB 为等腰直角三角形,理由见解析;
(2)EF的长为5;
(3)存在,M点坐标为(0,-6),理由见解析.
【分析】(1)利用,可知a,b的值,从而知道点A、B的坐标,继而推导出△OAH与△BAH是两个全等的等腰直角三角形,最后得出△AOB 为等腰直角三角形;
(2)将△AOE绕A点顺时针旋转90°得到△ABG,从而构造Rt △FBG,再用SAS证明△GAF≌△EAF(SAS),从而得到,最后设EF为x,构造方程解出即可;
(3)取取点C(3,0)关于y轴对称的对称点P(-3,0),利用∠FMO=2∠CMO得到PM是∠FMO 的角平分线,再用等面积法得出,再设OM=3t,利用勾股定理构造方程,解出方程推出M点坐标.
【详解】(1)△AOB 为等腰直角三角形,理由如下:
过点 A 作 AH⊥OB, 垂足为 H,
∵,
∴,
又∵A(a,),B (b,0),
∴,B,
∴OH= HB =AH=6.
又∵AH⊥OB,
∴△OAH与△BAH是两个全等的等腰直角三角形(SAS),
∴∠ABO=∠AOB=45°,AB=AO,∠BAO=∠BAH+∠OAH=45°+45°= 90°.
∴△AOB 为等腰直角三角形.
(2)将△AOE绕A点顺时针旋转90°得到△ABG,旋转后AO与AB重合,
则有∠ABG=∠AOE=45°,BG=OE,AG=AE,∠BAG=∠OAE,
∠FBG=∠ABO+∠ABG=45°+45°=90°,
.
又∵∠BAO= 90°,∠EAF=45°,
∴∠GAF=∠BAG+∠BAF=∠OAE +∠BAF=∠BAO-∠EAF=,
∴∠GAF=∠EAF.
∵AG=AE,∠GAF=∠EAF ,AF=AF,
∴△GAF≌△EAF(SAS),
∴FG=EF.
∵,
∴OE=3.
∵,FG=EF,BG=OE,
∴.
设EF=x,则BF=OB-OE-x=9-x,
∴,
解得:x=5,即EF的长为5.
(3)存在,M点坐标为,理由如下:
取点C(3,0)关于y轴对称的对称点P(-3,0),
由(2)知OF=EF+OE=8,
∴.
连接 MP, 过点 P 作 PK⊥MF, 垂足为 K,
∵OP=OC=3,
∴MO 垂直平分 CP,
∴MP=MC,∠CMO=∠PMO.
∵∠FMO=2∠CMO,
∴∠FMO=2∠PMO ,
∴,
∴PM是∠FMO 的角平分线.
又∵PK⊥MF,PO⊥OM,
∴PK=PO,
∴.
又∵,
∴.
设 MF=5t, 则 MO=3t,
∵,
∴,
∴(含去),
∴,MO=3t=6,
∴M 点的坐标为.
【点睛】本题考查等腰直角三角形的判定与性质,旋转的性质,等面积法,方程思想解决几何问题等知识,第二小问解题的关键是利用旋转构造直角三角形,第三小问解题的关键是等面积法推出与的比例关系.
22.(1)平分
(2)或
(3)不变,差值是
【分析】(1)设的反向延长线为,由角平分线的性质和对顶角的性质可求得;
(2)由直线恰好平分锐角可知旋转或时直线平分,根据旋转速度可求得需要的时间;
(3)由,可知,最后求得两角的差,从而可做出判断.
【详解】(1)解:直线平分.
理由如下:设的反向延长线为,
∵平分,
∴,
又,
∴,
∵,
∴,∴平分,
即直线平分,故答案为:平分;
(2)∵,∴.
∴.
即旋转或时直线ON平分∠AOC.
由题意得,或.
解得:或,
故答案为:或;
(3)的差不变.
∵,
∴,
∴.
∴与的差不变,这个差值是.
【点睛】本题考查了旋转的性质,角平分线的定义,几何图形中角度的计算,掌握旋转的性质,数形结合是解题的关键.
23.(1) AD=BE,AD⊥BE.(2) AD=BE,AD⊥BE.(3) 5-3≤PC≤5+3.
【分析】(1)根据等腰三角形性质证△ACD≌△BCE(SAS),得AD=BE,∠EBC=∠CAD,延长BE交AD于点F,由垂直定义得AD⊥BE.
(2)根据等腰三角形性质证△ACD≌△BCE(SAS),AD=BE,∠CAD=∠CBE,由垂直定义得∠OHB=90°,AD⊥BE;
(3)作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,PC=BE,当P、E、B共线时,BE最小,最小值=PB-PE;当P、E、B共线时,BE最大,最大值=PB+PE,故5-3≤BE≤5+3.
【详解】(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
故答案为AD=BE,AD⊥BE.
(2)结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-3,
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3,
∴5-3≤BE≤5+3,
即5-3≤PC≤5+3.
【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.
24.(1)作图如图所示,点B的坐标为(-2,1)
(2)作图如图所示
(3)存在点,使得PA+PC的值最小.
【分析】(1)根据A、C 的坐标确定平面直角坐标系的原点位置,从而画出平面直角坐标系,并得到点B的坐标
(2)根据旋转的定义作图即可
(3)根据图形对称性质,作点C关于x轴的对称点C2,连接A C2,则A C2交x轴于点P,此时PA+PC的值最小.此时由A(-3,5),C2(0,-3),求得直线A C2的解析式,进而求出直线A C2与x轴的交点,即得P点坐标.
【详解】(1)解:由A、C 的坐标分别为A(-3,5)、C(0,3),可得平面直角坐标系如图所示,点B的坐标为(-2,1).
(2)解:作图如图所示,
(3)解:存在点,使得PA+PC的值最小.
作点C关于x轴的对称点C2,连接A C2,则A C2交x轴于点P,此时PA+PC的值最小.
∵C(0,3),点C2为点C关于x轴的对称点,
∴C2(0,-3),
∵ A(-3,5),C2(0,-3),
设直线A C2的解析式为:,将A(-3,5),C2(0,-3)代入解析式中,
可得,,
解得,,
∴直线A C2的解析式为:,
令,得,
故存在,使得PA+PC的值最小.
【点睛】本题考查了平面直角坐标系,图形的旋转及对称性质,熟练掌握图形的旋转及对称变换是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
