2024-2025学年北师大版七年级数学下册2.2探索直线平行的条件课时2 利用内错角、同旁内角判定两直线平行 课件(共31张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册2.2探索直线平行的条件课时2 利用内错角、同旁内角判定两直线平行 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 740.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 07:44:15 | ||
图片预览








文档简介
(共31张PPT)
北师大版七年级数学下册课件
第二章 相交线与平行线
2.2 探索直线平行的条件
课时2 利用内错角、同旁内角判定两直线平行
1.理解内错角、同旁内角的概念;
2.结合图形识别内错角、同旁内角;(重点)
3.会运用内错角、同旁内角判定两条直线平行.(难点)
学习目标
新课讲解
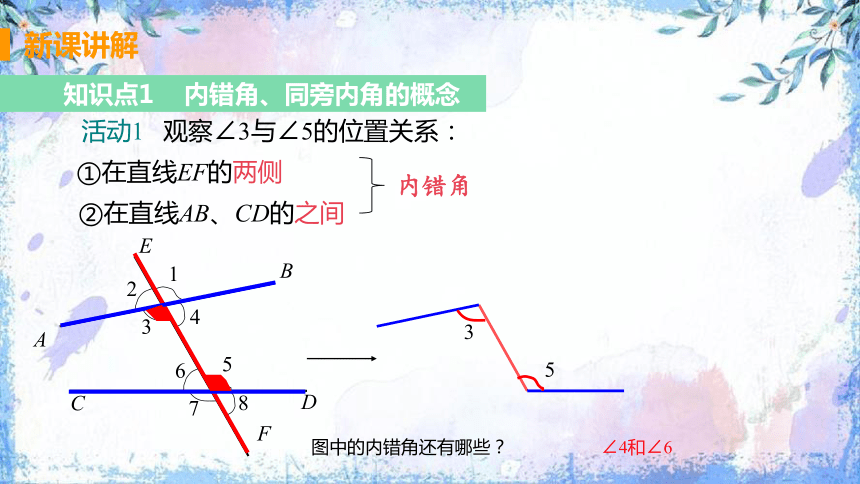
知识点1 内错角、同旁内角的概念
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
新课讲解
截线 被截线 结构
特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
总结归纳
新课讲解
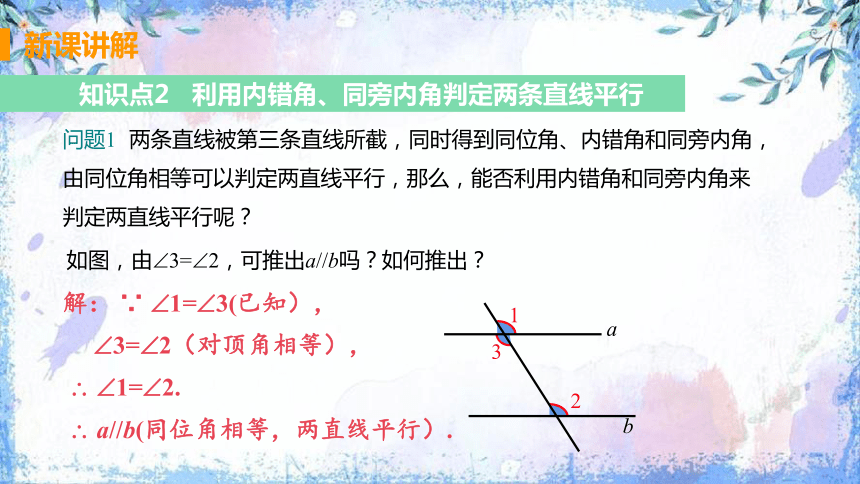
知识点2 利用内错角、同旁内角判定两条直线平行
问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3= 2,可推出a//b吗?如何推出?
解: ∵ 1= 3(已知),
3= 2(对顶角相等),
1= 2.
a//b(同位角相等,两直线平行).
2
b
a
1
3
新课讲解
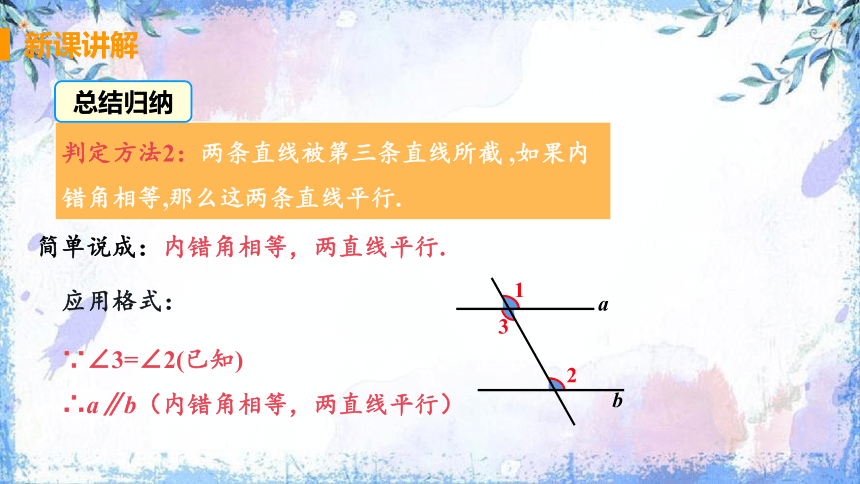
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
2
b
a
1
3
∵∠3=∠2(已知)
∴a∥b(内错角相等,两直线平行)
应用格式:
总结归纳
新课讲解
问题2 如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角定义)
2= 3(同角的补角相等)
a//b(同位角相等,两直线平行)
2
b
a
1
3
新课讲解
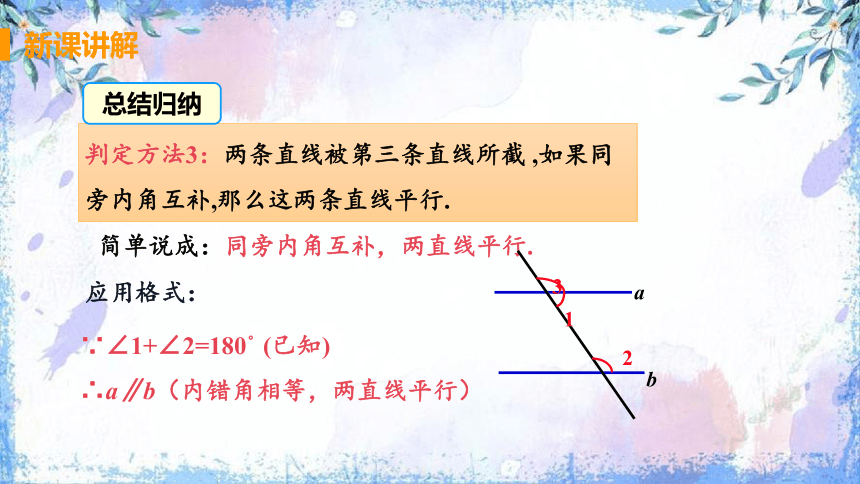
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知)
∴a∥b(内错角相等,两直线平行)
总结归纳
新课讲解
内错角相等,两直线平行
同旁内角互补,两直线平行
结论
新课讲解
内错角相等,两直线平行
同旁内角互补,两直线平行
结论
课堂小结
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
________相等 两直线平行 ∵ (已知) ∴a∥b
_________互补 两直线平行 ∵ (已知) ∴a∥b
当堂小练
1.如图,∠1=30°,∠2或∠3满足条件
___________________,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
当堂小练
2.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
知识点一:内错角、同旁内角
(1)内错角的特征:两个角都在直线a,b之间,并且被截线c错开(如图).
举例:如图,互为内错角的是:
∠3和 ;∠4和 .
形状:“Z”字形.
∠5
∠6
(2)同旁内角的特征:两个角都在直线 a ,b之间,并且都在截线c的同一旁.
举例:如图,互为同旁内角的是:
∠3和 ; ∠4和 .
形状:“U”字形.
∠6
∠5
(1)同位角有 ;
(2)内错角有 ;
(3)同旁内角有 .
∠3和∠5,∠4和∠6
∠3和∠6,∠4和∠5
1.(北师7下P44、人教7下P7)如图,直线a与b被c所截.
∠1和∠5,∠3和∠7,∠2和∠6,∠4和∠8
(3)几何语言:如图,
因为 ,
所以 .
a∥b
知识点二:两条直线平行的条件2
(1)两条直线被第三条直线所截,如果 相等,那么这两条直线平行.
简称为: .
(2)图示:(“Z”字形)
∠1=∠2
内错角相等,两直线平行
内错角
2.如图,已知∠1=60°,∠2=60°,试说明a∥b.
解:因为∠1=60°,∠2=60°(已知),
所以∠1=∠2(等量代换).
所以a∥b(内错角相等,两直线平行).
知识点三:两条直线平行的条件3
(1)两条直线被第三条直线所截,如果同旁内角 ,那么这两条直线平行.
简称为: .
(2)图示:(“U”字形)
(3)几何语言:如图,
因为 ,
所以 .
a∥b
∠1+∠2=180°
同旁内角互补,两直线平行
互补
3.如图,已知∠1=110°,∠2=70°,试说明AB∥CD.
解:因为∠1=110°,∠2=70°,
所以∠1+∠2=180°,所以AB∥CD.
4.【例1】如图,∠1=40°,当∠2= °时,a∥b.
40
5.【例2】(北师7下P53、人教7下P17)如图,当∠1+∠2=180°时,直线a,b平行吗 为什么 (可尝试用多种方法解答)
答案图
解:当∠1+∠2=180°时,a∥b,
理由如下:
如图,因为∠1+∠2=180°,
且∠3+∠2=180°,
所以∠1=∠3,所以a∥b.(其他方法略)
6.【例3】如图,点A,B,E在同一直线上,已知AD平分∠CAE,∠C=∠2.试说明:AD∥BC.
解:因为AD平分∠CAE,所以∠1=∠2.
因为∠C=∠2,所以∠1=∠C,所以AD∥BC.
7.【例4】如图,当∠B+∠D=∠BED时,AB∥CD吗 请说明理由.
解:AB∥CD,理由如下:
如图,延长BE交CD于F,
因为∠BED=180°-∠FED=180°-
(180°-∠EFD-∠D)=∠EFD+∠D,
又因为∠BED=∠B+∠D,
所以∠B=∠EFD.
所以AB∥CD.
答案图
8.(北师7下P54、人教7下P15)如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,则AB与CD的位置关系是 ,根据是 .
同旁内角互补,两直线平行
平行
9.如图,CE⊥DG,垂足为C,∠CAB=125°,∠ACE=145°.试说明CD∥AB.
解:因为CE⊥DG,所以∠ECG=90°.
因为∠ACE=145°,所以∠ACG=∠ACE-∠ECG=55°.
因为∠CAB=125°,所以∠CAB+∠ACG=180°.
所以AB∥DG,即CD∥AB.
10.如图,已知∠1=∠2,∠3+∠4=180°,试说明AC∥FG.
解:因为∠1=∠2,
所以AC∥DE.
因为∠3+∠4=180°,
所以DE∥FG,
所以AC∥FG.
★11.(人教7下P23改编)如图,已知∠B+∠BCD+∠D=360°,则AB∥ED,为什么
解:如图,延长ED,BC交于点F,
因为∠BCD=180°-∠DCF
=180°-(180°-∠CDF-∠F)=∠CDF+∠F,
又因为∠B+∠BCD+∠EDC=360°,
所以∠B+∠CDF+∠F+∠EDC=360°.
因为∠CDF+∠EDC=180°,
所以∠B+∠F=180°.所以AB∥ED.
布置作业
请完成课后对应习题
感谢大家观看
北师大版七年级数学下册课件
第二章 相交线与平行线
2.2 探索直线平行的条件
课时2 利用内错角、同旁内角判定两直线平行
1.理解内错角、同旁内角的概念;
2.结合图形识别内错角、同旁内角;(重点)
3.会运用内错角、同旁内角判定两条直线平行.(难点)
学习目标
新课讲解
知识点1 内错角、同旁内角的概念
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
新课讲解
截线 被截线 结构
特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
总结归纳
新课讲解
知识点2 利用内错角、同旁内角判定两条直线平行
问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3= 2,可推出a//b吗?如何推出?
解: ∵ 1= 3(已知),
3= 2(对顶角相等),
1= 2.
a//b(同位角相等,两直线平行).
2
b
a
1
3
新课讲解
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
2
b
a
1
3
∵∠3=∠2(已知)
∴a∥b(内错角相等,两直线平行)
应用格式:
总结归纳
新课讲解
问题2 如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角定义)
2= 3(同角的补角相等)
a//b(同位角相等,两直线平行)
2
b
a
1
3
新课讲解
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知)
∴a∥b(内错角相等,两直线平行)
总结归纳
新课讲解
内错角相等,两直线平行
同旁内角互补,两直线平行
结论
新课讲解
内错角相等,两直线平行
同旁内角互补,两直线平行
结论
课堂小结
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
________相等 两直线平行 ∵ (已知) ∴a∥b
_________互补 两直线平行 ∵ (已知) ∴a∥b
当堂小练
1.如图,∠1=30°,∠2或∠3满足条件
___________________,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
当堂小练
2.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
知识点一:内错角、同旁内角
(1)内错角的特征:两个角都在直线a,b之间,并且被截线c错开(如图).
举例:如图,互为内错角的是:
∠3和 ;∠4和 .
形状:“Z”字形.
∠5
∠6
(2)同旁内角的特征:两个角都在直线 a ,b之间,并且都在截线c的同一旁.
举例:如图,互为同旁内角的是:
∠3和 ; ∠4和 .
形状:“U”字形.
∠6
∠5
(1)同位角有 ;
(2)内错角有 ;
(3)同旁内角有 .
∠3和∠5,∠4和∠6
∠3和∠6,∠4和∠5
1.(北师7下P44、人教7下P7)如图,直线a与b被c所截.
∠1和∠5,∠3和∠7,∠2和∠6,∠4和∠8
(3)几何语言:如图,
因为 ,
所以 .
a∥b
知识点二:两条直线平行的条件2
(1)两条直线被第三条直线所截,如果 相等,那么这两条直线平行.
简称为: .
(2)图示:(“Z”字形)
∠1=∠2
内错角相等,两直线平行
内错角
2.如图,已知∠1=60°,∠2=60°,试说明a∥b.
解:因为∠1=60°,∠2=60°(已知),
所以∠1=∠2(等量代换).
所以a∥b(内错角相等,两直线平行).
知识点三:两条直线平行的条件3
(1)两条直线被第三条直线所截,如果同旁内角 ,那么这两条直线平行.
简称为: .
(2)图示:(“U”字形)
(3)几何语言:如图,
因为 ,
所以 .
a∥b
∠1+∠2=180°
同旁内角互补,两直线平行
互补
3.如图,已知∠1=110°,∠2=70°,试说明AB∥CD.
解:因为∠1=110°,∠2=70°,
所以∠1+∠2=180°,所以AB∥CD.
4.【例1】如图,∠1=40°,当∠2= °时,a∥b.
40
5.【例2】(北师7下P53、人教7下P17)如图,当∠1+∠2=180°时,直线a,b平行吗 为什么 (可尝试用多种方法解答)
答案图
解:当∠1+∠2=180°时,a∥b,
理由如下:
如图,因为∠1+∠2=180°,
且∠3+∠2=180°,
所以∠1=∠3,所以a∥b.(其他方法略)
6.【例3】如图,点A,B,E在同一直线上,已知AD平分∠CAE,∠C=∠2.试说明:AD∥BC.
解:因为AD平分∠CAE,所以∠1=∠2.
因为∠C=∠2,所以∠1=∠C,所以AD∥BC.
7.【例4】如图,当∠B+∠D=∠BED时,AB∥CD吗 请说明理由.
解:AB∥CD,理由如下:
如图,延长BE交CD于F,
因为∠BED=180°-∠FED=180°-
(180°-∠EFD-∠D)=∠EFD+∠D,
又因为∠BED=∠B+∠D,
所以∠B=∠EFD.
所以AB∥CD.
答案图
8.(北师7下P54、人教7下P15)如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,则AB与CD的位置关系是 ,根据是 .
同旁内角互补,两直线平行
平行
9.如图,CE⊥DG,垂足为C,∠CAB=125°,∠ACE=145°.试说明CD∥AB.
解:因为CE⊥DG,所以∠ECG=90°.
因为∠ACE=145°,所以∠ACG=∠ACE-∠ECG=55°.
因为∠CAB=125°,所以∠CAB+∠ACG=180°.
所以AB∥DG,即CD∥AB.
10.如图,已知∠1=∠2,∠3+∠4=180°,试说明AC∥FG.
解:因为∠1=∠2,
所以AC∥DE.
因为∠3+∠4=180°,
所以DE∥FG,
所以AC∥FG.
★11.(人教7下P23改编)如图,已知∠B+∠BCD+∠D=360°,则AB∥ED,为什么
解:如图,延长ED,BC交于点F,
因为∠BCD=180°-∠DCF
=180°-(180°-∠CDF-∠F)=∠CDF+∠F,
又因为∠B+∠BCD+∠EDC=360°,
所以∠B+∠CDF+∠F+∠EDC=360°.
因为∠CDF+∠EDC=180°,
所以∠B+∠F=180°.所以AB∥ED.
布置作业
请完成课后对应习题
感谢大家观看
同课章节目录
