8.3.1 分类变量与列联表-课后提升训练(含解析)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.3.1 分类变量与列联表-课后提升训练(含解析)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册 | 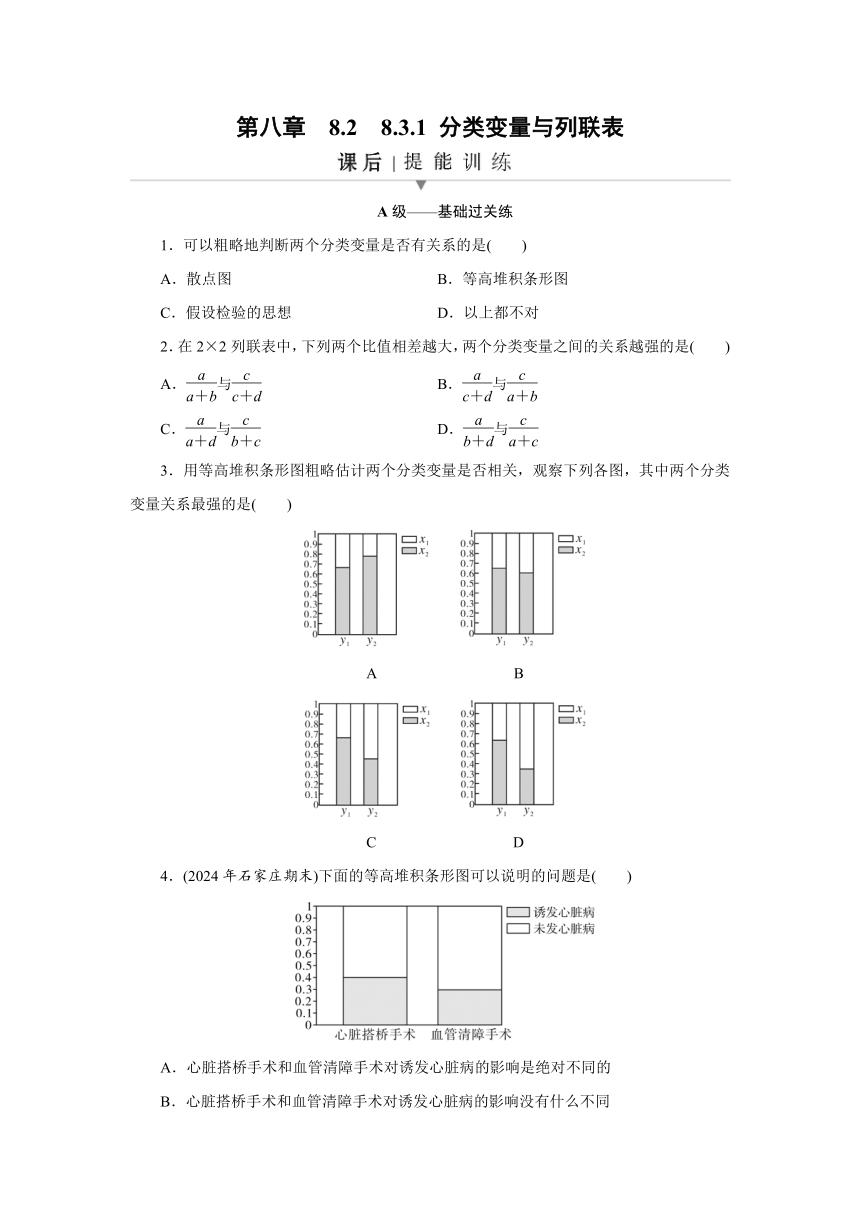 | |
| 格式 | docx | ||
| 文件大小 | 442.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 09:49:06 | ||
图片预览




文档简介
第八章 8.2 8.3.1 分类变量与列联表
A级——基础过关练
1.可以粗略地判断两个分类变量是否有关系的是( )
A.散点图 B.等高堆积条形图
C.假设检验的思想 D.以上都不对
2.在2×2列联表中,下列两个比值相差越大,两个分类变量之间的关系越强的是( )
A.与 B.与
C.与 D.与
3.用等高堆积条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
A B
C D
4.(2024年石家庄期末)下面的等高堆积条形图可以说明的问题是( )
A.心脏搭桥手术和血管清障手术对诱发心脏病的影响是绝对不同的
B.心脏搭桥手术和血管清障手术对诱发心脏病的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.心脏搭桥手术和血管清障手术对诱发心脏病的影响在某种程度上是不同的,但是没有100%的把握
5.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:
项目 男 女 合计
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c等于( )
A.7 B.8
C.9 D.10
6.(2024年福州期末)(多选)户外运动已经成为一种时尚,某单位为了了解员工喜欢户外运动是否与性别有关联,从本单位所有员工共计650人中采用比例分配的分层随机抽样的方法抽取50人进行问卷调查,得到了如下2×2列联表:
单位:人
性别 户外运动 合计
喜欢 不喜欢
男性 a 5 b
女性 10 c d
合计 e f 50
在这50人中随机抽取1人,抽到喜欢户外运动员工的概率是0.6,则下列说法正确的是( )
A.抽取的50人中喜欢户外运动的有30人
B.a=20,c=15
C.e=30,f=10
D.女性中喜欢户外运动的频率为0.4
7.某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集的数据是_________.
8.(2024年新乡期中)下图是调查某学校高一、高二年级学生参加社团活动的等高堆积条形图,阴影部分的高表示参加社团的频率.已知该校高一、高二年级学生人数均为600(所有学生都参加了调查),现从参加社团的同学中按分层随机抽样的方式抽取45人,则抽取的高二学生人数为________.
9.下表是不完整的2×2列联表,其中3a=c,b=2d,则a=________.
类别 y1 y2 合计
x1 a b 55
x2 c d
合计 120
10.为了解铅中毒病人与尿棕色素为阳性是否有关系,分别对病人组和对照组的尿液作尿棕色素定性检查,结果如下:
组别 尿棕色素 合计
阳性数 阴性数
铅中毒病人 29 7 36
对照组 9 28 37
合计 38 35 73
试画出列联表的等高堆积条形图,分析铅中毒病人和对照组的尿棕色素阳性数有无差别,铅中毒病人与尿棕色素为阳性是否有关系.
B级——能力提升练
11.(多选)为了解市民对地铁1号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高堆积条形图:
根据图中(35岁以上含35岁)的信息,下列结论中一定正确的有( )
A.样本中男性比女性更关注地铁1号线全线开通
B.样本中多数女性是35岁以上
C.样本中35岁以下的男性人数比35岁以上的女性人数多
D.样本中35岁以上的人对地铁1号线的开通关注度更高
12.为了考察长头发与女性头晕是否有关系,随机抽查301名女性,得到如下列联表,试根据表格中已有数据填空.
头发类型 头晕状况 合计
经常头晕 很少头晕
长发 35 ① 121
短发 37 143 ②
合计 72 ③ ④
空格中的数据应分别为:①__________;②________;③________;④________.
13.某校在高一部分学生中调查男女同学对某项体育运动的喜欢情况,其二维堆积条形图如图所示(阴影部分代表喜欢,白色代表不喜欢).
(1)写出2×2列联表;
(2)在这次调查中,从喜欢这项体育运动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
C级——创新拓展练
14.针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.根据题中数据,完成列联表.
类别 是否产生抗体 合计
产生抗体 未产生抗体
甲
乙
合计
参考答案
【A级——基础过关练】
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D 【解析】由等高堆积条形图可知心脏搭桥手术和血管清障手术对诱发心脏病的频率不同,所以心脏搭桥手术和血管清障手术对诱发心脏病的影响在某种程度上是不同的,但是没有100%的把握,所以选项D正确.故选D.
5.【答案】C 【解析】根据题意,可得c=120-73-25=22,a=74-22=52,b=73-52=21,∴a-b-c=52-21-22=9.故选C.
6.【答案】ABD 【解析】从50人中随机抽取1人,抽到喜欢户外运动员工的概率是0.6,可得50人中喜欢户外运动的人数为50×0.6=30,即e=30,f=20.因为喜欢户外运动的女性有10人,所以喜欢户外运动的男性有30-10=20人,即a=20,b=25.因为不喜欢户外运动的男性有5人,所以不喜欢户外运动的女性有20-5=15人,即c=15,d=25.女性中喜欢户外运动的频率为=0.4.故选ABD.
7.【答案】男正教授人数,副教授人数;女正教授人数,副教授人数
8.【答案】27 【解析】根据等高堆积条形图可知,参加社团的高一和高二年级学生的人数比为2∶3,由分层随机抽样的性质可得抽取的高二学生人数为45×=27.
9.【答案】15 【解析】由题意得又因为3a=c,b=2d,所以解得a=15.
10.解:等高堆积条形图如图所示:
其中两个白色条的高分别代表铅中毒病人和对照组样本中尿棕色素为阳性的频率.
由图可以直观地看出铅中毒病人与对照组相比,尿棕色素为阳性的频率差异明显,因此铅中毒病人与尿棕色素为阳性有关系.
【B级——能力提升练】
11.【答案】ABD 【解析】设等高堆积条形图对应2×2列联表如下:
性别 35岁以上 35岁以下 合计
男性 a c a+c
女性 b d b+d
合计 a+b c+d a+b+c+d
根据第1个等高堆积条形图可知,35岁以上男性比35岁以上女性多,即a>b;35岁以下男性比35岁以下女性多,即c>d.根据第2个等高堆积条形图可知,男性中35岁以上的比35岁以下的多,即a>c;女性中35岁以上的比35岁以下的多,即b>d.对于A,男性人数为a+c,女性人数为b+d,因为a>b,c>d,所以a+c>b+d,所以A正确;对于B,35岁以上女性人数为b,35岁以下女性人数为d,因为b>d,所以B正确;对于C,35岁以下男性人数为c,35岁以上女性人数为b,无法从图中直接判断b与c的大小关系,所以C不一定正确;对于D,35岁以上的人数为a+b,35岁以下的人数为c+d,因为a>c,b>d,所以a+b>c+d,所以D正确.故选ABD.
12.【答案】86 180 229 301 【解析】最右侧的合计是对应的行上的两个数据的和,由此可求出①和②;而最下面的合计是相应的列上两个数据的和,由①和②的结果可求得③④.
13.解:(1)观察二维堆积条形图可得,
经调查的男生总共45人,其中喜欢这项运动的有15人,不喜欢的有30人;
经调查的女生总共45人,其中喜欢这项运动的有5人,不喜欢的有40人.
由此写出列联表如下:
性别 某项运动 合计
喜欢 不喜欢
男 15 30 45
女 5 40 45
合计 20 70 90
(2)所求概率为p==,
即恰是一男一女的概率为.
【C级——创新拓展练】
14.解:由题意可得未产生该新型病毒抗体的志愿者的人数为100×=10,
则注射甲种疫苗的志愿者中未产生抗体的人数为10×=2,
产生抗体的人数为50-2=48,
注射乙种疫苗的志愿者中未产生抗体的人数为10-2=8,
产生抗体的人数为50-8=42.
所得列联表如下.
类别 是否产生抗体 合计
产生抗体 未产生抗体
甲 48 2 50
乙 42 8 50
合计 90 10 100
A级——基础过关练
1.可以粗略地判断两个分类变量是否有关系的是( )
A.散点图 B.等高堆积条形图
C.假设检验的思想 D.以上都不对
2.在2×2列联表中,下列两个比值相差越大,两个分类变量之间的关系越强的是( )
A.与 B.与
C.与 D.与
3.用等高堆积条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
A B
C D
4.(2024年石家庄期末)下面的等高堆积条形图可以说明的问题是( )
A.心脏搭桥手术和血管清障手术对诱发心脏病的影响是绝对不同的
B.心脏搭桥手术和血管清障手术对诱发心脏病的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.心脏搭桥手术和血管清障手术对诱发心脏病的影响在某种程度上是不同的,但是没有100%的把握
5.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:
项目 男 女 合计
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c等于( )
A.7 B.8
C.9 D.10
6.(2024年福州期末)(多选)户外运动已经成为一种时尚,某单位为了了解员工喜欢户外运动是否与性别有关联,从本单位所有员工共计650人中采用比例分配的分层随机抽样的方法抽取50人进行问卷调查,得到了如下2×2列联表:
单位:人
性别 户外运动 合计
喜欢 不喜欢
男性 a 5 b
女性 10 c d
合计 e f 50
在这50人中随机抽取1人,抽到喜欢户外运动员工的概率是0.6,则下列说法正确的是( )
A.抽取的50人中喜欢户外运动的有30人
B.a=20,c=15
C.e=30,f=10
D.女性中喜欢户外运动的频率为0.4
7.某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集的数据是_________.
8.(2024年新乡期中)下图是调查某学校高一、高二年级学生参加社团活动的等高堆积条形图,阴影部分的高表示参加社团的频率.已知该校高一、高二年级学生人数均为600(所有学生都参加了调查),现从参加社团的同学中按分层随机抽样的方式抽取45人,则抽取的高二学生人数为________.
9.下表是不完整的2×2列联表,其中3a=c,b=2d,则a=________.
类别 y1 y2 合计
x1 a b 55
x2 c d
合计 120
10.为了解铅中毒病人与尿棕色素为阳性是否有关系,分别对病人组和对照组的尿液作尿棕色素定性检查,结果如下:
组别 尿棕色素 合计
阳性数 阴性数
铅中毒病人 29 7 36
对照组 9 28 37
合计 38 35 73
试画出列联表的等高堆积条形图,分析铅中毒病人和对照组的尿棕色素阳性数有无差别,铅中毒病人与尿棕色素为阳性是否有关系.
B级——能力提升练
11.(多选)为了解市民对地铁1号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高堆积条形图:
根据图中(35岁以上含35岁)的信息,下列结论中一定正确的有( )
A.样本中男性比女性更关注地铁1号线全线开通
B.样本中多数女性是35岁以上
C.样本中35岁以下的男性人数比35岁以上的女性人数多
D.样本中35岁以上的人对地铁1号线的开通关注度更高
12.为了考察长头发与女性头晕是否有关系,随机抽查301名女性,得到如下列联表,试根据表格中已有数据填空.
头发类型 头晕状况 合计
经常头晕 很少头晕
长发 35 ① 121
短发 37 143 ②
合计 72 ③ ④
空格中的数据应分别为:①__________;②________;③________;④________.
13.某校在高一部分学生中调查男女同学对某项体育运动的喜欢情况,其二维堆积条形图如图所示(阴影部分代表喜欢,白色代表不喜欢).
(1)写出2×2列联表;
(2)在这次调查中,从喜欢这项体育运动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
C级——创新拓展练
14.针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.根据题中数据,完成列联表.
类别 是否产生抗体 合计
产生抗体 未产生抗体
甲
乙
合计
参考答案
【A级——基础过关练】
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D 【解析】由等高堆积条形图可知心脏搭桥手术和血管清障手术对诱发心脏病的频率不同,所以心脏搭桥手术和血管清障手术对诱发心脏病的影响在某种程度上是不同的,但是没有100%的把握,所以选项D正确.故选D.
5.【答案】C 【解析】根据题意,可得c=120-73-25=22,a=74-22=52,b=73-52=21,∴a-b-c=52-21-22=9.故选C.
6.【答案】ABD 【解析】从50人中随机抽取1人,抽到喜欢户外运动员工的概率是0.6,可得50人中喜欢户外运动的人数为50×0.6=30,即e=30,f=20.因为喜欢户外运动的女性有10人,所以喜欢户外运动的男性有30-10=20人,即a=20,b=25.因为不喜欢户外运动的男性有5人,所以不喜欢户外运动的女性有20-5=15人,即c=15,d=25.女性中喜欢户外运动的频率为=0.4.故选ABD.
7.【答案】男正教授人数,副教授人数;女正教授人数,副教授人数
8.【答案】27 【解析】根据等高堆积条形图可知,参加社团的高一和高二年级学生的人数比为2∶3,由分层随机抽样的性质可得抽取的高二学生人数为45×=27.
9.【答案】15 【解析】由题意得又因为3a=c,b=2d,所以解得a=15.
10.解:等高堆积条形图如图所示:
其中两个白色条的高分别代表铅中毒病人和对照组样本中尿棕色素为阳性的频率.
由图可以直观地看出铅中毒病人与对照组相比,尿棕色素为阳性的频率差异明显,因此铅中毒病人与尿棕色素为阳性有关系.
【B级——能力提升练】
11.【答案】ABD 【解析】设等高堆积条形图对应2×2列联表如下:
性别 35岁以上 35岁以下 合计
男性 a c a+c
女性 b d b+d
合计 a+b c+d a+b+c+d
根据第1个等高堆积条形图可知,35岁以上男性比35岁以上女性多,即a>b;35岁以下男性比35岁以下女性多,即c>d.根据第2个等高堆积条形图可知,男性中35岁以上的比35岁以下的多,即a>c;女性中35岁以上的比35岁以下的多,即b>d.对于A,男性人数为a+c,女性人数为b+d,因为a>b,c>d,所以a+c>b+d,所以A正确;对于B,35岁以上女性人数为b,35岁以下女性人数为d,因为b>d,所以B正确;对于C,35岁以下男性人数为c,35岁以上女性人数为b,无法从图中直接判断b与c的大小关系,所以C不一定正确;对于D,35岁以上的人数为a+b,35岁以下的人数为c+d,因为a>c,b>d,所以a+b>c+d,所以D正确.故选ABD.
12.【答案】86 180 229 301 【解析】最右侧的合计是对应的行上的两个数据的和,由此可求出①和②;而最下面的合计是相应的列上两个数据的和,由①和②的结果可求得③④.
13.解:(1)观察二维堆积条形图可得,
经调查的男生总共45人,其中喜欢这项运动的有15人,不喜欢的有30人;
经调查的女生总共45人,其中喜欢这项运动的有5人,不喜欢的有40人.
由此写出列联表如下:
性别 某项运动 合计
喜欢 不喜欢
男 15 30 45
女 5 40 45
合计 20 70 90
(2)所求概率为p==,
即恰是一男一女的概率为.
【C级——创新拓展练】
14.解:由题意可得未产生该新型病毒抗体的志愿者的人数为100×=10,
则注射甲种疫苗的志愿者中未产生抗体的人数为10×=2,
产生抗体的人数为50-2=48,
注射乙种疫苗的志愿者中未产生抗体的人数为10-2=8,
产生抗体的人数为50-8=42.
所得列联表如下.
类别 是否产生抗体 合计
产生抗体 未产生抗体
甲 48 2 50
乙 42 8 50
合计 90 10 100
