8.3.2 独立性检验-课后提升训练(含解析)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.3.2 独立性检验-课后提升训练(含解析)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 09:49:14 | ||
图片预览



文档简介
第八章 8.2 8.3.2 独立性检验
A级——基础过关练
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.零假设H0:男性喜欢参加体育活动
B.零假设H0:女性不喜欢参加体育活动
C.零假设H0:喜欢参加体育活动与性别有关
D.零假设H0:喜欢参加体育活动与性别无关
2.(2024年汕头期中)利用独立性检验对两个随机事件是否有关系进行研究时,若根据α=0.005的独立性检验认为“X与Y有关系”,则具体计算出的数据应该是( )
A.χ2≥6.635 B.χ2<6.635
C.χ2≥7.879 D.χ2<7.879
3.为了考察某种中成药预防流感的效果,抽样调查40人,得到如下数据:
药物 流感
患流感 未患流感
服用 2 18
未服用 8 12
根据表中数据,计算χ2的值为( )
A.2.4 B.4.8
C.24 D.48
4.考察棉花种子是否经过处理跟生病之间的关系得到有关数据,根据数据计算得χ2=0.164,则根据小概率值α=0.1的独立性检验,下列判断正确的是( )
A.种子是否经过处理跟是否生病有关
B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病
D.以上都是错误的
5.为加强高三学生的素质教育,促进学生全面发展,某校对高三学生文化课与体育课的成绩进行了调查统计,结果如下:
文化课 体育课 合计
不及格 及格
及格 57 221 278
不及格 16 43 59
合计 73 264 337
在探究体育课成绩和文化课成绩是否相关时,根据以上数据可得到χ2约为( )
A.0.004 B.1.255
C.2.058 D.38.214
6.(2024年滨州期末)(多选)为考查某种营养品对儿童身高增长的影响,选取部分儿童进行试验,根据100个有放回简单随机样本的数据,得到如下列联表,由表可知下列说法正确的有( )
营养品 身高 合计
有明显增长 无明显增长
食用 a 10 50
未食用 b 30 50
合计 60 40 100
A.a=40
B.b=20
C.χ2≈12.667
D.根据小概率值α=0.001的独立性检验,可以认为该营养品对儿童身高增长有影响
7.根据分类变量x与y的观察数据,计算得到χ2=2.974,根据小概率值α=0.05的独立性检验,分析变量x与y__________(填“相互独立”或“不相互独立”).
8.(2024年烟台期末)已知P(χ2≥6.635)=0.01,P(χ2≥10.828)=0.001.在检验喜欢某项体育运动与性别是否有关的过程中,某研究员搜集数据并计算得到χ2=7.235,则根据小概率值α=________的χ2独立性检验,分析喜欢该项体育运动与性别有关.
9.(2024年长春期中)针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则男生至少有______人.
参考数据及公式如下:
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
参考公式:χ2=,其中n=a+b+c+d.
10.(2024年潮州期末)人的性格可以大体分为“外向型”和“内向型”两种,树人中学为了了解这两种性格特征与人的性别是否存在关联,采用简单随机抽样的方法抽取90名学生,得到如下数据:
性别 外向型 内向型
男性 45 15
女性 20 10
(1)以上述统计结果的频率估计概率,从该校男生中随机抽取2人、女生中随机抽取1人担任志愿者.设这三人中性格外向型的人数为X,求X的数学期望.
(2)对表格中的数据,依据α=0.1的独立性检验,可以得出独立性检验的结论是这两种性格特征与人的性别没有关联.如果将表格中的所有数据都扩大为原来10倍,在相同的检验标准下,再用独立性检验推断这两种性格特征与人的性别之间的关联性,得到的结论是否一致?请说明理由.
附:参考公式:
χ2=.
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
B级——能力提升练
11.(多选)有两个分类变量X,Y,其列联表如下:
X Y 合计
Y=y1 Y=y2
X=x1 a 20-a 20
X=x2 15-a 30+a 45
合计 15 50 65
其中a,15-a均为大于5的整数,若依据α=0.05的独立性检验可以认为Y与X有关,则a的可能取值为( )
A.6 B.7
C.8 D.9
12.(2024年海南期末)某制药公司为了验证一种药物对治疗“抑郁症”是否有效,随机选取了100名抑郁症患者进行试验,并根据试验数据得到下列2×2列联表:
项目 用药 未用药
症状明显减轻 37 33
症状没有减轻 8 22
根据表中数据,计算可得χ2=________(结果精确到0.001),依据小概率值α=________ (填临界值表中符合条件的最小值)的独立性检验,可以认为该药物对治疗“抑郁症”是有效的.
附:χ2=.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
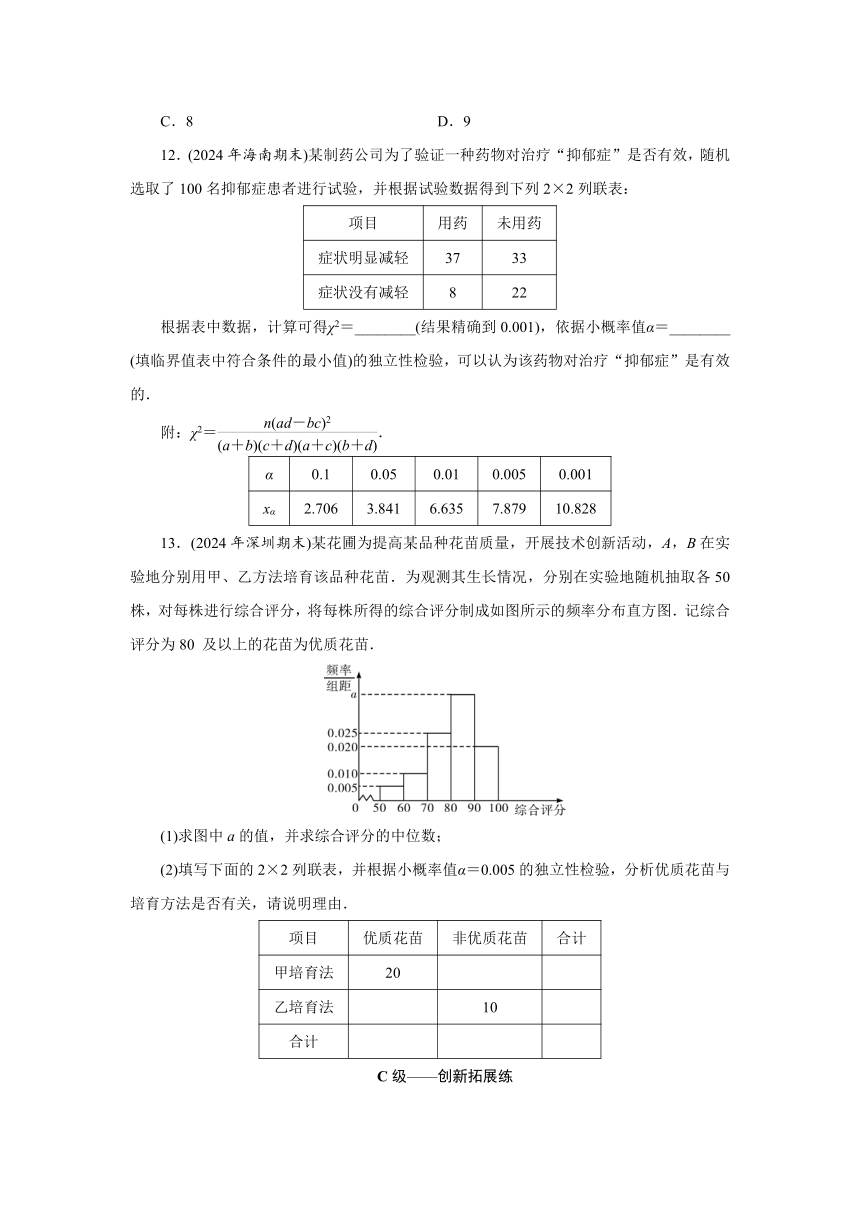
13.(2024年深圳期末)某花圃为提高某品种花苗质量,开展技术创新活动,A,B在实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80 及以上的花苗为优质花苗.
(1)求图中a的值,并求综合评分的中位数;
(2)填写下面的2×2列联表,并根据小概率值α=0.005的独立性检验,分析优质花苗与培育方法是否有关,请说明理由.
项目 优质花苗 非优质花苗 合计
甲培育法 20
乙培育法 10
合计
C级——创新拓展练
14.(2024年济南模拟)直播带货是助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力边远地区农民增收.某边远地区有统计数据显示,2023年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示,一周内使用直播销售的频率分布扇形图如图2所示,若将销售主播按照年龄分为年轻人(20岁~39岁)和非年轻人(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为经常使用直播销售用户,使用次数为5次或不足5次的称为不常使用直播销售用户,且经常使用直播销售用户中有是年轻人.
图1 图2
现对该地相关居民进行“经常使用直播销售与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,完成下列2×2列联表,根据α=0.1的独立性检验,能否认为经常使用直播销售与年龄有关?
项目 年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
参考答案
【A级——基础过关练】
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B 【解析】由χ2=0.164<2.706=x0.1,即没有充分证据认为种子是否经过处理跟是否生病有关.
5.【答案】B 【解析】由题中数据,知χ2=≈1.255.故选B.
6.【答案】ABD 【解析】a=50-10=40,A正确;b=60-a=60-40=20,B正确;零假设为H0:该营养品对儿童身高增长无影响,因为χ2=≈16.667>10.828=x0.001,所以根据小概率值α=0.001的独立性检验,推断H0不成立,即可以认为该营养品对儿童身高增长有影响,C错误,D正确.
7.【答案】相互独立 【解析】χ2=2.974<3.841=x0.05,所以分析变量x与y相互独立.
8.【答案】0.01 【解析】因为6.635<7.235<10.828,所以根据小概率值α=0.01的χ2独立性检验,分析喜欢该项体育运动与性别有关.
9.【答案】30 【解析】设男生人数为x,依题意可得列联表如下:
类别 喜欢追星 不喜欢追星 合计
男生 x
女生
合计
根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则χ2>3.841,由χ2==x>3.841,解得x>25.61,由题知x应为6的整数倍,∴根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则男生至少有30人.
10.解:(1)由统计结果可知,外向型男生在所有男生中占比为,外向型女生在所有女生中占比为,
故从该校男生中随机抽取一人为外向型男生的概率是,从该校女生中随机抽取一人为外向型女生的概率是.
(方法一)X的所有可能取值为0,1,2,3,
则P(X=0)=×=,P(X=1)=C×××+×=,
P(X=2)=×+C×××=,P(X=3)=×=,
所以E(X)=0×+1×+2×+3×=.
(方法二)从该校男生中随机抽取2人,抽到性格外向型的人数记为Y1,
从该校女生中随机抽取1人,抽到性格外向型的人数记为Y2,则Y1~B,Y2~B,
所以E(Y1)=2×=,E(Y2)=1×=.
所以E(X)=E(Y1+Y2)=E(Y1)+E(Y2)=+=.
(2)零假设为H0:这两种性格特征与人的性别无关联.
由所获得的所有数据都扩大为原来10倍,
可知χ2==≈6.923>2.706=x0.1,
依据α=0.1的独立性检验,可以推断这两种性格特征与人的性别有关联,与原来的结论不一致,
原因是每个数据扩大为原来的10倍,相当于样本量变大为原来的10倍,导致推断结论发生了变化.
【B级——能力提升练】
11.【答案】CD 【解析】根据a>5且15-a>5,a∈Z,知a可取6,7,8,9,由表中数据及题意,得χ2=≥3.841=x0.05,知a可能取值为8,9.
12.【答案】5.820 0.05 【解析】由2×2列联表中数据得χ2==≈5.820,因为5.820>3.841=x0.05,所以α=0.05.
13.解:(1)由直方图的性质,得0.005×10+0.010×10+0.025×10+10a+0.020×10=1,解得a=0.040.
因为(0.02+0.04)×10=0.6>0.5,所以中位数位于[80,90)内,
设中位数为x,则有0.020×10+0.040×(90-x)=0.5,解得x=82.5.
故综合评分的中位数为82.5.
(2)由(1)得优质花苗的频率为0.6,
所以样本中优质花苗的数量为60,
得如下列联表:
项目 优质花苗 非优质花苗 合计
甲培育法 20 30 50
乙培育法 40 10 50
合计 60 40 100
零假设为H0:优质花苗与培育方法无关,
χ2=≈16.667>7.879=x0.005,
所以根据小概率值α=0.005的独立性检验,推断H0不成立,即认为优质花苗与培育方法有关.
【C级——创新拓展练】
14.解:由题图1知年轻人有200×(45.5%+34.5%)=160(人),
非年轻人有200-160=40(人).
由题图2知经常使用直播销售用户有200×(30.1%+19.2%+10.7%)=120(人),
不常使用直播销售用户有200-120=80(人),
经常使用直播销售用户中的年轻人有120×=100(人),
经常使用直播销售用户中的非年轻人有120-100=20(人).
补全列联表如下:
项目 年轻人 非年轻人 合计
经常使用直播销售用户 100 20 120
不常使用直播销售用户 60 20 80
合计 160 40 200
零假设为H0:经常使用直播销售与年龄无关.
χ2==≈2.083<2.706=x0.1.
根据小概率值α=0.1的独立性检验,无充分证据认为H0不成立,我们推断H0成立,即认为经常使用直播销售与年龄无关.
A级——基础过关练
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.零假设H0:男性喜欢参加体育活动
B.零假设H0:女性不喜欢参加体育活动
C.零假设H0:喜欢参加体育活动与性别有关
D.零假设H0:喜欢参加体育活动与性别无关
2.(2024年汕头期中)利用独立性检验对两个随机事件是否有关系进行研究时,若根据α=0.005的独立性检验认为“X与Y有关系”,则具体计算出的数据应该是( )
A.χ2≥6.635 B.χ2<6.635
C.χ2≥7.879 D.χ2<7.879
3.为了考察某种中成药预防流感的效果,抽样调查40人,得到如下数据:
药物 流感
患流感 未患流感
服用 2 18
未服用 8 12
根据表中数据,计算χ2的值为( )
A.2.4 B.4.8
C.24 D.48
4.考察棉花种子是否经过处理跟生病之间的关系得到有关数据,根据数据计算得χ2=0.164,则根据小概率值α=0.1的独立性检验,下列判断正确的是( )
A.种子是否经过处理跟是否生病有关
B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病
D.以上都是错误的
5.为加强高三学生的素质教育,促进学生全面发展,某校对高三学生文化课与体育课的成绩进行了调查统计,结果如下:
文化课 体育课 合计
不及格 及格
及格 57 221 278
不及格 16 43 59
合计 73 264 337
在探究体育课成绩和文化课成绩是否相关时,根据以上数据可得到χ2约为( )
A.0.004 B.1.255
C.2.058 D.38.214
6.(2024年滨州期末)(多选)为考查某种营养品对儿童身高增长的影响,选取部分儿童进行试验,根据100个有放回简单随机样本的数据,得到如下列联表,由表可知下列说法正确的有( )
营养品 身高 合计
有明显增长 无明显增长
食用 a 10 50
未食用 b 30 50
合计 60 40 100
A.a=40
B.b=20
C.χ2≈12.667
D.根据小概率值α=0.001的独立性检验,可以认为该营养品对儿童身高增长有影响
7.根据分类变量x与y的观察数据,计算得到χ2=2.974,根据小概率值α=0.05的独立性检验,分析变量x与y__________(填“相互独立”或“不相互独立”).
8.(2024年烟台期末)已知P(χ2≥6.635)=0.01,P(χ2≥10.828)=0.001.在检验喜欢某项体育运动与性别是否有关的过程中,某研究员搜集数据并计算得到χ2=7.235,则根据小概率值α=________的χ2独立性检验,分析喜欢该项体育运动与性别有关.
9.(2024年长春期中)针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则男生至少有______人.
参考数据及公式如下:
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
参考公式:χ2=,其中n=a+b+c+d.
10.(2024年潮州期末)人的性格可以大体分为“外向型”和“内向型”两种,树人中学为了了解这两种性格特征与人的性别是否存在关联,采用简单随机抽样的方法抽取90名学生,得到如下数据:
性别 外向型 内向型
男性 45 15
女性 20 10
(1)以上述统计结果的频率估计概率,从该校男生中随机抽取2人、女生中随机抽取1人担任志愿者.设这三人中性格外向型的人数为X,求X的数学期望.
(2)对表格中的数据,依据α=0.1的独立性检验,可以得出独立性检验的结论是这两种性格特征与人的性别没有关联.如果将表格中的所有数据都扩大为原来10倍,在相同的检验标准下,再用独立性检验推断这两种性格特征与人的性别之间的关联性,得到的结论是否一致?请说明理由.
附:参考公式:
χ2=.
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
B级——能力提升练
11.(多选)有两个分类变量X,Y,其列联表如下:
X Y 合计
Y=y1 Y=y2
X=x1 a 20-a 20
X=x2 15-a 30+a 45
合计 15 50 65
其中a,15-a均为大于5的整数,若依据α=0.05的独立性检验可以认为Y与X有关,则a的可能取值为( )
A.6 B.7
C.8 D.9
12.(2024年海南期末)某制药公司为了验证一种药物对治疗“抑郁症”是否有效,随机选取了100名抑郁症患者进行试验,并根据试验数据得到下列2×2列联表:
项目 用药 未用药
症状明显减轻 37 33
症状没有减轻 8 22
根据表中数据,计算可得χ2=________(结果精确到0.001),依据小概率值α=________ (填临界值表中符合条件的最小值)的独立性检验,可以认为该药物对治疗“抑郁症”是有效的.
附:χ2=.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
13.(2024年深圳期末)某花圃为提高某品种花苗质量,开展技术创新活动,A,B在实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80 及以上的花苗为优质花苗.
(1)求图中a的值,并求综合评分的中位数;
(2)填写下面的2×2列联表,并根据小概率值α=0.005的独立性检验,分析优质花苗与培育方法是否有关,请说明理由.
项目 优质花苗 非优质花苗 合计
甲培育法 20
乙培育法 10
合计
C级——创新拓展练
14.(2024年济南模拟)直播带货是助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力边远地区农民增收.某边远地区有统计数据显示,2023年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示,一周内使用直播销售的频率分布扇形图如图2所示,若将销售主播按照年龄分为年轻人(20岁~39岁)和非年轻人(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为经常使用直播销售用户,使用次数为5次或不足5次的称为不常使用直播销售用户,且经常使用直播销售用户中有是年轻人.
图1 图2
现对该地相关居民进行“经常使用直播销售与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,完成下列2×2列联表,根据α=0.1的独立性检验,能否认为经常使用直播销售与年龄有关?
项目 年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
参考答案
【A级——基础过关练】
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B 【解析】由χ2=0.164<2.706=x0.1,即没有充分证据认为种子是否经过处理跟是否生病有关.
5.【答案】B 【解析】由题中数据,知χ2=≈1.255.故选B.
6.【答案】ABD 【解析】a=50-10=40,A正确;b=60-a=60-40=20,B正确;零假设为H0:该营养品对儿童身高增长无影响,因为χ2=≈16.667>10.828=x0.001,所以根据小概率值α=0.001的独立性检验,推断H0不成立,即可以认为该营养品对儿童身高增长有影响,C错误,D正确.
7.【答案】相互独立 【解析】χ2=2.974<3.841=x0.05,所以分析变量x与y相互独立.
8.【答案】0.01 【解析】因为6.635<7.235<10.828,所以根据小概率值α=0.01的χ2独立性检验,分析喜欢该项体育运动与性别有关.
9.【答案】30 【解析】设男生人数为x,依题意可得列联表如下:
类别 喜欢追星 不喜欢追星 合计
男生 x
女生
合计
根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则χ2>3.841,由χ2==x>3.841,解得x>25.61,由题知x应为6的整数倍,∴根据小概率值α=0.05的独立性检验,判断中学生追星与性别有关,则男生至少有30人.
10.解:(1)由统计结果可知,外向型男生在所有男生中占比为,外向型女生在所有女生中占比为,
故从该校男生中随机抽取一人为外向型男生的概率是,从该校女生中随机抽取一人为外向型女生的概率是.
(方法一)X的所有可能取值为0,1,2,3,
则P(X=0)=×=,P(X=1)=C×××+×=,
P(X=2)=×+C×××=,P(X=3)=×=,
所以E(X)=0×+1×+2×+3×=.
(方法二)从该校男生中随机抽取2人,抽到性格外向型的人数记为Y1,
从该校女生中随机抽取1人,抽到性格外向型的人数记为Y2,则Y1~B,Y2~B,
所以E(Y1)=2×=,E(Y2)=1×=.
所以E(X)=E(Y1+Y2)=E(Y1)+E(Y2)=+=.
(2)零假设为H0:这两种性格特征与人的性别无关联.
由所获得的所有数据都扩大为原来10倍,
可知χ2==≈6.923>2.706=x0.1,
依据α=0.1的独立性检验,可以推断这两种性格特征与人的性别有关联,与原来的结论不一致,
原因是每个数据扩大为原来的10倍,相当于样本量变大为原来的10倍,导致推断结论发生了变化.
【B级——能力提升练】
11.【答案】CD 【解析】根据a>5且15-a>5,a∈Z,知a可取6,7,8,9,由表中数据及题意,得χ2=≥3.841=x0.05,知a可能取值为8,9.
12.【答案】5.820 0.05 【解析】由2×2列联表中数据得χ2==≈5.820,因为5.820>3.841=x0.05,所以α=0.05.
13.解:(1)由直方图的性质,得0.005×10+0.010×10+0.025×10+10a+0.020×10=1,解得a=0.040.
因为(0.02+0.04)×10=0.6>0.5,所以中位数位于[80,90)内,
设中位数为x,则有0.020×10+0.040×(90-x)=0.5,解得x=82.5.
故综合评分的中位数为82.5.
(2)由(1)得优质花苗的频率为0.6,
所以样本中优质花苗的数量为60,
得如下列联表:
项目 优质花苗 非优质花苗 合计
甲培育法 20 30 50
乙培育法 40 10 50
合计 60 40 100
零假设为H0:优质花苗与培育方法无关,
χ2=≈16.667>7.879=x0.005,
所以根据小概率值α=0.005的独立性检验,推断H0不成立,即认为优质花苗与培育方法有关.
【C级——创新拓展练】
14.解:由题图1知年轻人有200×(45.5%+34.5%)=160(人),
非年轻人有200-160=40(人).
由题图2知经常使用直播销售用户有200×(30.1%+19.2%+10.7%)=120(人),
不常使用直播销售用户有200-120=80(人),
经常使用直播销售用户中的年轻人有120×=100(人),
经常使用直播销售用户中的非年轻人有120-100=20(人).
补全列联表如下:
项目 年轻人 非年轻人 合计
经常使用直播销售用户 100 20 120
不常使用直播销售用户 60 20 80
合计 160 40 200
零假设为H0:经常使用直播销售与年龄无关.
χ2==≈2.083<2.706=x0.1.
根据小概率值α=0.1的独立性检验,无充分证据认为H0不成立,我们推断H0成立,即认为经常使用直播销售与年龄无关.
