8.3.1 柱体、锥体、台体的表面积与体积 课后训练(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.3.1 柱体、锥体、台体的表面积与体积 课后训练(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 118.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 10:25:52 | ||
图片预览


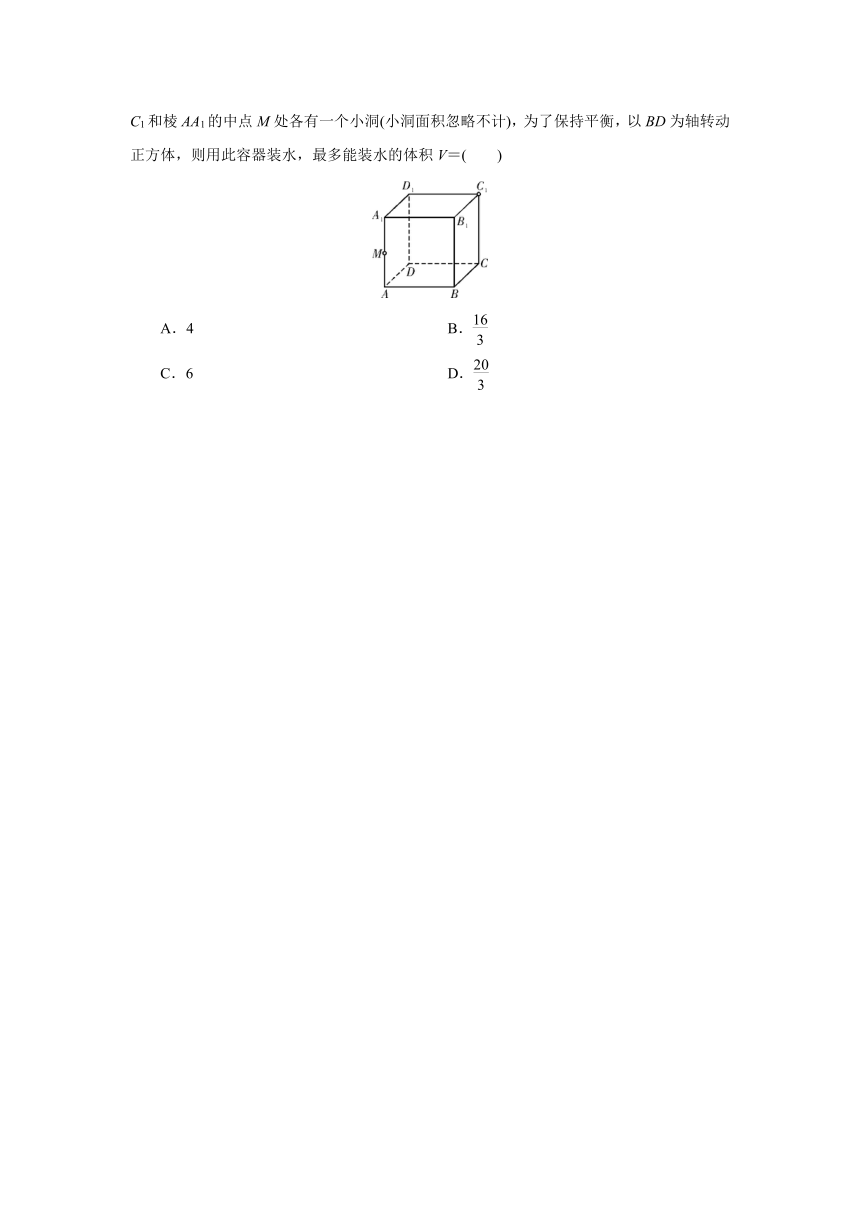
文档简介
第八章 8.3 柱体、锥体、台体的表面积与体积
A级——基础过关练
1.正方体的表面积为96,则正方体的体积为( )
A.48 B.64
C.16 D.96
2.已知圆柱OO1及其展开图如图所示,则其体积为( )
A.π B.2π
C.3π D.4π
3.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
A.4π B.3π
C.2π D.π
4.若正三棱锥的底面边长等于a,三条侧棱两两垂直,则它的侧面积为( )
A.a2 B.a2
C.a2 D.3a2
5.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )
A.π B.2π
C.4π D.8π
6.(多选)已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.该几何体的体积和侧面积分别用V和S表示,则( )
A.V=64 B.V=32
C.S=40+24 D.S=40+12
7.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为________m3,侧面积为________m2.
8.(2024年日照东港区期中)如图,在正四棱台ABCD-A1B1C1D1中,已知AB=2,A1B1=1,且棱台的侧面积为6,则该棱台的高为________.
9.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.
10.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积.
B级——综合运用练
11.(2024年福清模拟)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,且该圆锥的母线是底面半径的倍,若△SAB的面积为5,则该圆锥的表面积为( )
A.40π B.(40+40)π
C.80π D.(40+80)π
12.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
13.一个圆锥的底面半径为2 cm,高为6 cm,在其内部有一个高为x cm的内接圆柱.
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大?并求出侧面积的最大值.
C级——创新拓展练
14.(2024年佛山模拟)木桶效应,也可称为短板效应,是说一只水桶能装多少水取决于它最短的那块木板.如果一只桶的木板中有一块不齐或者某块木板有破洞,这只桶就无法盛满水,此时我们可以倾斜木桶,设法让桶装水更多.如图,棱长为2的正方体容器,在顶点C1和棱AA1的中点M处各有一个小洞(小洞面积忽略不计),为了保持平衡,以BD为轴转动正方体,则用此容器装水,最多能装水的体积V=( )
A.4 B.
C.6 D.
参考答案
【A级——基础过关练】
1.【答案】B
【解析】设正方体的棱长为a,则6a2=96,∴a=4,故V=a3=43=64.
2.【答案】D
【解析】设底面半径为r,高为h,根据展开图得则所以圆柱的体积为πr2h=π×12×4=4π.故选D.
3.【答案】C
【解析】底面圆半径为1,高为1,侧面积S=2πrh=2π×1×1=2π.故选C.
4.【答案】A
【解析】因为正三棱锥的底面边长等于a,三条侧棱两两垂直,所以三棱锥的侧棱长为a,则它的侧面3××a×a=a2.
5.【答案】B
【解析】设圆柱的底面半径为r,则圆柱的母线长为2r,由题意得S圆柱侧=2πr×2r=4πr2=4π,解得r=1,所以V圆柱=πr2×2r=2πr3=2π.故选B.
6.【答案】AC
【解析】几何体的体积为V=·S矩形·h=×6×8×4=64.正侧面及相对侧面底边上的高为h1==5.左、右侧面的底边上的高为h2==4.故几何体的侧面面积S=2×=40+24.
7.【答案】 3
【解析】设正六棱柱的底面边长为a m,高为h m,则2ah=1,a=1,解得a=,h=.所以六棱柱的体积V=××6×=(m3),S侧=6××=3(m2).
8.【答案】
【解析】在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,如图,设斜高为h′,则侧面积为4××(1+2)h′=6,解得h′=1,所以该棱台的高为h==.
9.【答案】168π
【解析】先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r,下底面半径为R,则它的母线长为l===5r=10,所以r=2,R=8.故S侧=π(R+r)l=π(8+2)×10=100π,S表=S侧+πr2+πR2=100π+4π+64π=168π.
10.解:设圆锥的底面半径为r,母线为l,
则2πr=πl,得l=6r.
又因为S锥=πr2+πr·6r=7πr2=15π,解得r=,
所以圆锥的高h====5.
所以V=πr2h=π××5=π.
【B级——能力提升练】
11.【答案】B
【解析】设圆锥的底面圆半径为r,则母线长为l=r,因为母线SA,SB所成角θ的余弦值为,且θ∈(0,π),所以sin θ==,所以△SAB的面积为×(r)2×=5,解得r=2,所以母线长为l=×2=4,所以该圆锥的表面积为S=πr2+πrl=π×(2)2+π×2×4=(40+40)π.故选B.
12.【答案】90 138
【解析】该几何体的体积V=4×6×3+×4×3×3=90,表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.
13.解:(1)圆锥的母线长为=2(cm),
∴圆锥的侧面积S1=π×2×2=4π(cm2).
(2)画出圆锥的轴截面如图所示.
设圆柱的底面半径为r cm,由题意,知=,
∴r=,∴圆柱的侧面积S2=2πrx=(-x2+6x)=-[(x-3)2-9],∴当x=3时,圆柱的侧面积取得最大值,且最大值为6π cm2.
【C级——创新拓展练】
14.【答案】C
【解析】如图,以BD为轴转动正方体,要使能装水最多,则水面平行BD且经过MC1,设水面与棱BB1,DD1的交点分别为E,F,即多面体ABCD-MEC1F的体积.∵M为棱AA1的中点,∴B1E=D1F=,∴多面体ABCD-MEC1F的体积V=2×2×1+×2×2×+×2××+××2×2×=6.故选C.
A级——基础过关练
1.正方体的表面积为96,则正方体的体积为( )
A.48 B.64
C.16 D.96
2.已知圆柱OO1及其展开图如图所示,则其体积为( )
A.π B.2π
C.3π D.4π
3.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
A.4π B.3π
C.2π D.π
4.若正三棱锥的底面边长等于a,三条侧棱两两垂直,则它的侧面积为( )
A.a2 B.a2
C.a2 D.3a2
5.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )
A.π B.2π
C.4π D.8π
6.(多选)已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.该几何体的体积和侧面积分别用V和S表示,则( )
A.V=64 B.V=32
C.S=40+24 D.S=40+12
7.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为________m3,侧面积为________m2.
8.(2024年日照东港区期中)如图,在正四棱台ABCD-A1B1C1D1中,已知AB=2,A1B1=1,且棱台的侧面积为6,则该棱台的高为________.
9.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.
10.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积.
B级——综合运用练
11.(2024年福清模拟)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,且该圆锥的母线是底面半径的倍,若△SAB的面积为5,则该圆锥的表面积为( )
A.40π B.(40+40)π
C.80π D.(40+80)π
12.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
13.一个圆锥的底面半径为2 cm,高为6 cm,在其内部有一个高为x cm的内接圆柱.
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大?并求出侧面积的最大值.
C级——创新拓展练
14.(2024年佛山模拟)木桶效应,也可称为短板效应,是说一只水桶能装多少水取决于它最短的那块木板.如果一只桶的木板中有一块不齐或者某块木板有破洞,这只桶就无法盛满水,此时我们可以倾斜木桶,设法让桶装水更多.如图,棱长为2的正方体容器,在顶点C1和棱AA1的中点M处各有一个小洞(小洞面积忽略不计),为了保持平衡,以BD为轴转动正方体,则用此容器装水,最多能装水的体积V=( )
A.4 B.
C.6 D.
参考答案
【A级——基础过关练】
1.【答案】B
【解析】设正方体的棱长为a,则6a2=96,∴a=4,故V=a3=43=64.
2.【答案】D
【解析】设底面半径为r,高为h,根据展开图得则所以圆柱的体积为πr2h=π×12×4=4π.故选D.
3.【答案】C
【解析】底面圆半径为1,高为1,侧面积S=2πrh=2π×1×1=2π.故选C.
4.【答案】A
【解析】因为正三棱锥的底面边长等于a,三条侧棱两两垂直,所以三棱锥的侧棱长为a,则它的侧面3××a×a=a2.
5.【答案】B
【解析】设圆柱的底面半径为r,则圆柱的母线长为2r,由题意得S圆柱侧=2πr×2r=4πr2=4π,解得r=1,所以V圆柱=πr2×2r=2πr3=2π.故选B.
6.【答案】AC
【解析】几何体的体积为V=·S矩形·h=×6×8×4=64.正侧面及相对侧面底边上的高为h1==5.左、右侧面的底边上的高为h2==4.故几何体的侧面面积S=2×=40+24.
7.【答案】 3
【解析】设正六棱柱的底面边长为a m,高为h m,则2ah=1,a=1,解得a=,h=.所以六棱柱的体积V=××6×=(m3),S侧=6××=3(m2).
8.【答案】
【解析】在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,如图,设斜高为h′,则侧面积为4××(1+2)h′=6,解得h′=1,所以该棱台的高为h==.
9.【答案】168π
【解析】先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r,下底面半径为R,则它的母线长为l===5r=10,所以r=2,R=8.故S侧=π(R+r)l=π(8+2)×10=100π,S表=S侧+πr2+πR2=100π+4π+64π=168π.
10.解:设圆锥的底面半径为r,母线为l,
则2πr=πl,得l=6r.
又因为S锥=πr2+πr·6r=7πr2=15π,解得r=,
所以圆锥的高h====5.
所以V=πr2h=π××5=π.
【B级——能力提升练】
11.【答案】B
【解析】设圆锥的底面圆半径为r,则母线长为l=r,因为母线SA,SB所成角θ的余弦值为,且θ∈(0,π),所以sin θ==,所以△SAB的面积为×(r)2×=5,解得r=2,所以母线长为l=×2=4,所以该圆锥的表面积为S=πr2+πrl=π×(2)2+π×2×4=(40+40)π.故选B.
12.【答案】90 138
【解析】该几何体的体积V=4×6×3+×4×3×3=90,表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.
13.解:(1)圆锥的母线长为=2(cm),
∴圆锥的侧面积S1=π×2×2=4π(cm2).
(2)画出圆锥的轴截面如图所示.
设圆柱的底面半径为r cm,由题意,知=,
∴r=,∴圆柱的侧面积S2=2πrx=(-x2+6x)=-[(x-3)2-9],∴当x=3时,圆柱的侧面积取得最大值,且最大值为6π cm2.
【C级——创新拓展练】
14.【答案】C
【解析】如图,以BD为轴转动正方体,要使能装水最多,则水面平行BD且经过MC1,设水面与棱BB1,DD1的交点分别为E,F,即多面体ABCD-MEC1F的体积.∵M为棱AA1的中点,∴B1E=D1F=,∴多面体ABCD-MEC1F的体积V=2×2×1+×2×2×+×2××+××2×2×=6.故选C.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
