第八章 立体几何初步 章末检测(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 第八章 立体几何初步 章末检测(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 280.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 10:37:04 | ||
图片预览




文档简介
第八章 立体几何初步
章末检测
(时间:120分钟,满分150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线l与平面α不平行,则( )
A.l与α相交 B.l α
C.l与α相交或l α D.以上结论都不对
2.(2024年封开月考)某圆锥母线长为1,其侧面积与轴截面面积的比值为2π,则该圆锥体积为( )
A. B.
C. D.
3.(2024年平果模拟)如图,一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形,已知直观图OA′B′C′中,B′C′=1,OC′=,则该平面图形的面积为( )
A. B.2
C.2 D.4
4.如图,正四棱锥P-ABCD的体积为2,底面积为6,E为侧棱PC的中点,则直线BE与平面PAC所成的角为( )
A.30° B.45°
C.60° D.90°
5.(2024年扬州模拟)已知某圆锥底面半径为1,高为2,则该圆锥的外接球表面积为( )
A.π B.π
C.π D.π
6.(2024年石家庄月考)已知m,n是两条不同的直线,α,β是两个不同的平面,则m∥α的一个充分条件是( )
A.m∥n,n∥α B.m∥β,α∥β
C.m⊥n,n⊥α,m α D.m∩n=A,n∥α,m α
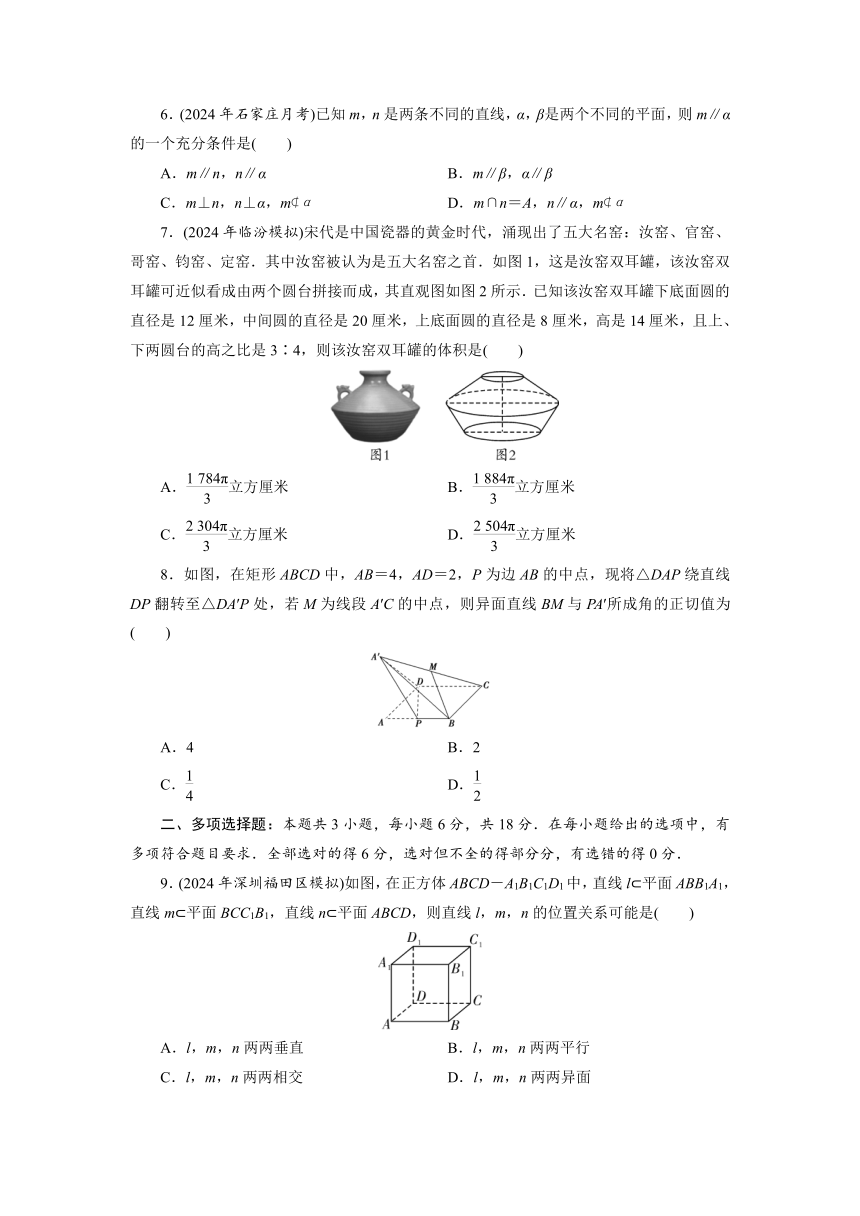
7.(2024年临汾模拟)宋代是中国瓷器的黄金时代,涌现出了五大名窑:汝窑、官窑、哥窑、钧窑、定窑.其中汝窑被认为是五大名窑之首.如图1,这是汝窑双耳罐,该汝窑双耳罐可近似看成由两个圆台拼接而成,其直观图如图2所示.已知该汝窑双耳罐下底面圆的直径是12厘米,中间圆的直径是20厘米,上底面圆的直径是8厘米,高是14厘米,且上、下两圆台的高之比是3∶4,则该汝窑双耳罐的体积是( )
A.立方厘米 B.立方厘米
C.立方厘米 D.立方厘米
8.如图,在矩形ABCD中,AB=4,AD=2,P为边AB的中点,现将△DAP绕直线DP翻转至△DA′P处,若M为线段A′C的中点,则异面直线BM与PA′所成角的正切值为( )
A.4 B.2
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9.(2024年深圳福田区模拟)如图,在正方体ABCD-A1B1C1D1中,直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,则直线l,m,n的位置关系可能是( )
A.l,m,n两两垂直 B.l,m,n两两平行
C.l,m,n两两相交 D.l,m,n两两异面
10.(2024年江门蓬江区月考)下列命题中正确的有( )
A.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为16π
B.圆柱形容器底半径为5 cm,两直径为5 cm的玻璃球都浸没在容器的水中,若取出这两个小球,则容器内水面下降的高度为 cm
C.正四棱台的上、下底面边长分别为2,4,侧棱长为2,其体积为
D.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为π
11.(2024年紫金期中)如图,在底面为等边三角形的直三棱柱ABC-A1B1C1中,AC=2,BB1=,D,E分别为棱BC,BB1的中点,则( )
A.A1B∥平面ADC1
B.AD⊥C1D
C.异面直线AC与DE所成角的余弦值为
D.平面ADC1与平面ABC的夹角的正切值为
三、填空题:本题共3小题,每小题5分,共15分.
12.(2024年聊城期中)五棱台的顶点数为V,棱数为E,面数为F,则V+F-E=________.
13.(2024年中山月考)已知球O是某圆锥内可放入的最大的球,其半径为该圆锥底面半径的一半,则该圆锥的体积与球O的体积的比值为________.
14.(2024年佛山高明区月考)某同学将一张圆心角为的扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,已知OB=2OA=60 cm,则制成的简易笔筒的体积为________cm3.
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图,平面ABEF⊥平面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC綉AD,BE綉FA,G,H分别为FA,FD的中点.
(1)求证:四边形BCHG是平行四边形;
(2)C,D,F,E四点是否共面?请说明理由.
16.(15分)(2024年封丘月考)如图,在正方体A1B1C1D1-ABCD中,E是DD1的中点.
(1)求证:D1B∥平面ACE;
(2)设正方体的棱长为1,求三棱锥B-AEC的体积.
17.(15分)如图,在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连接ED,EC,EB和DB.(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.
18.(17分)(2024年江门新会区月考)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=2,O是AC与BD的交点,PO⊥平面ABCD,PO=2,M是PD的中点.
(1)求证:PB∥平面ACM;
(2)求证:平面PBC⊥平面PAC;
(3)求直线AM与平面ABCD所成角的正切值.
19.(17分)(2024年深圳中学月考)如图,在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,P为侧棱SD上的点,且SP=3PD.
(1)求正四棱锥S-ABCD的表面积.
(2)若M为SA的中点,求平面BMD与平面ABCD所成的二面角的余弦值.
(3)侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求的值;若不存在,试说明理由.
参考答案
选择题
1.【答案】C
【解析】直线与平面的位置关系有:直线在平面内、直线与平面平行、直线与平面相交.因为直线l与平面α不平行,所以l与α相交或l α.
2.【答案】B
【解析】设该圆锥的底面半径为r,高h==,由侧面积与轴截面面积的比值为2π,可得=2π,解得r=,h==,则该圆锥的体积V圆锥=π××=.故选B.
3.【答案】D
【解析】因为直观图是底角为45°的等腰梯形,且B′C′=1,OC′=,所以等腰梯形的高h=OC′sin 45°=×=1,所以等腰梯形的面积S′=×(1+1+1+1)×1=2,所以原平面图形的面积S=2S′=2×2=4.故选D.
4.【答案】C
【解析】如图,在正四棱锥P-ABCD中,根据底面积为6,可得BC=.连接BD交AC于点O,连接PO,OE,则PO为正四棱锥P-ABCD的高,根据体积公式可得PO=1.因为PO⊥底面ABCD,所以PO⊥BD.又因为BD⊥AC,PO∩AC=O,所以BD⊥平面PAC.连接EO,则∠BEO为直线BE与平面PAC所成的角.在Rt△POA中,因为PO=1,OA=,所以PA=2,OE=PA=1.在Rt△BOE中,因为BO=,所以tan ∠BEO==,即∠BEO=60°.故直线BE与平面PAC所成角为60°.
5.【答案】C
【解析】根据题意,设圆锥外接球的半径为r,则有r2=1+(2-r)2,解得r=,则该圆锥的外接球表面积S=4πr2=.故选C.
6.【答案】C
【解析】对于A,由m∥n,n∥α,可得m α或m∥α,故A错误;对于B,由m∥β,α∥β,可得m α或m∥α,故B错误;对于C,由m⊥n,n⊥α,m α,可得m∥α,故C正确;对于D,由m∩n=A,n∥α,m α,可得m,α相交或m∥α,故D错误.故选C.
7.【答案】D
【解析】∵上、下两圆台的高之比是3∶4,∴上圆台的高为14×=6厘米,下圆台的高为14×=8厘米,故上圆台的体积为V1=6×=312π 立方厘米,下圆台的体积为V2=8×=π 立方厘米,故该汝窑双耳罐的体积为V1+V2=312π+π=立方厘米.故选D.
8.【答案】D
【解析】如图,取A′D的中点N,连接PN,MN.∵M是A′C的中点,∴MN∥CD,且MN=CD.∵四边形ABCD是矩形,P是AB的中点,∴PB∥CD,且PB=CD.∴MN∥PB,且MN=PB.∴四边形PBMN为平行四边形.∴MB∥PN.∴∠A′PN(或其补角)是异面直线BM与PA′所成的角.在Rt△A′PN中,tan ∠A′PN==,∴异面直线BM与PA′所成角的正切值为.故选D.
多项选择题
9.【答案】ACD
【解析】如图,当l为BB1,m为BC,n为CD时,满足直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,l,m,n两两相交且垂直,当l为A1B,m为B1C1,n为AC时,三条直线两两异面,故A,C,D正确;三条直线不可能两两平行,若l∥n,则l∥AB∥n,而AB与平面BCC1B1相交,则AB与m不平行,故B错误.故选ACD.
10.【答案】BCD
【解析】对于A,截面小圆半径为1,则球的半径R==,该球的表面积为4πR2=8π,A错误;对于B,设容器内水面下降的高度为h,则52π·h=2××3,解得h=,B正确;对于C,正四棱台的高h′==,体积为(22++42)×=,C正确;对于D,设圆锥的底面圆半径r,则2πr=10×,解得r=4,圆锥的高h0==2,体积为π×42×2=π,D正确.故选BCD.
11.【答案】ABD
【解析】如图,对于A,连接A1C交AC1于F,连接DF,则DF∥A1B,因为A1B 平面ADC1,DF 平面ADC1,所以A1B∥平面ADC1,故A正确;对于B,由题可知AD⊥BC,因为平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,所以AD⊥平面BCC1B1,又C1D 平面BCC1B1,所以AD⊥C1D,故B正确;对于C,连接CB1,AB1,则CB1∥DE,∠ACB1为异面直线AC与DE所成的角(或其补角),由余弦定理可得cos ∠ACB1===,故异面直线AC与DE所成角的余弦值为,故C错误;对于D,由B的分析过程可知∠CDC1为平面ADC1与平面ABC的夹角的平面角,所以tan ∠CDC1==,故D正确.故选ABD.
填空题
12.【答案】2
【解析】根据题意,在五棱台中,V=10,E=15,F=7,则V+F-E=2.
13.【答案】
【解析】设球的半径为r,则圆锥的底面圆的半径为2r,设O与圆锥底面圆的连线与圆锥底面所成的角为θ,则母线与底面所成角为2θ,则tan θ=,∴tan 2θ==,∴圆锥的高为2r tan 2θ=,∴该圆锥的体积与球O的体积的比值为=.
14.【答案】
【解析】根据题意,设所得圆台的上底半径为r1,下底半径为r2,在图1的扇形中,OB=60 cm,OA=30 cm,圆心角为,则有=2πr1=OA×=10π,变形可得r1=5 cm,同理,=2πr2=OB×=20π,变形可得r2=10 cm,AB=OB-OA=30 cm,则圆台的高h===5 cm,故圆台的体积V=(100π+25π+)×5= cm3.
解答题
15.(1)证明:由题设知,FG=GA,FH=HD,所以GH綉AD.
又因为BC綉AD,所以GH綉BC.所以四边形BCHG是平行四边形.
(2)解:C,D,F,E四点共面.理由如下.
由BE綉FA,G是FA的中点,知BE綉GF.
所以EF綉BG.由(1)知BG∥CH,所以EF∥CH.故EC,FH共面.
又因为点D在直线FH上,所以C,D,F,E四点共面.
16.(1)证明:如图,连接BD交AC于点O,连接OE,
则O为BD的中点,又因为E是DD1的中点,
所以OE是△BDD1的中位线,所以OE∥D1B,
又因为OE 平面AEC,D1B 平面AEC,所以D1B∥平面AEC;
(2)解:正方体ABCD-A1B1C1D1中,易知D1D⊥平面ABCD,所以
V三棱锥B-AEC=V三棱锥E-ABC=S△ABC·ED=××AB×BC×ED=××1×1×=.
17.(1)证明:由题意可知△DD1E为等腰直角三角形,∠D1ED=45°.
同理,∠C1EC=45°.所以∠DEC=90°,即DE⊥EC.
又因为BC⊥平面D1DCC1,DE 平面D1DCC1,所以BC⊥DE.
又因为EC∩BC=C,所以DE⊥平面EBC.
因为DE 平面EDB,所以平面EDB⊥平面EBC.
(2)解:如图,过E作EO⊥DC于点O,过点O作OF⊥DB于点F,连接EF.
因为平面ABCD⊥平面D1DCC1,且交线为DC,
所以EO⊥平面ABCD,所以EO⊥OF,EO⊥BD.
由BD⊥OF,BD⊥OE,OF∩OE=O,得BD⊥平面EFO,所以BD⊥EF.
所以∠EFO为二面角E-DB-C的平面角.
在Rt△EFO中,易求得OF=,又因为OE=1,所以tan ∠EFO==.
所以二面角E-DB-C的正切值为.
18.(1)证明:在平行四边形ABCD中,∵O为AC与BD的交点,
∴O为BD的中点,又M为PD的中点,∴PB∥MO.
又∵PB 平面ACM,MO 平面ACM,∴PB∥平面ACM.
(2)证明:∵PO⊥平面ABCD,BC 平面ABCD,∴BC⊥PO.
在△ADC中,∵AD=AC,∴AD⊥AC.∵AD∥BC,∴BC⊥AC.
∵PO∩AC=O,PO 平面PAC,AC 平面PAC,∴BC⊥平面PAC.
又∵BC 平面PBC,∴平面PBC⊥平面PAC.
(3)解:如图,取DO的中点N,连接MN,AN,∵M为PD的中点,
∴MN∥PO,且MN=PO=1.
由PO⊥平面ABCD,得MN⊥平面ABCD,∴∠MAN是直线AM与平面ABCD所成的角.
∵∠ADC=45°,AD=AC=2,∠ACD=∠ADC=45°,∴∠CAD=90°.
在Rt△DAO中,AD=2,AO=AC=1,∴DO=,从而AN=DO=.在Rt△ANM中,tan ∠MAN===,∴直线AM与平面ABCD所成角的正切值为.
19.解:(1)在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,
则正四棱锥侧面的高为h==,
∴正四棱锥的表面积为S=4×××+×=8.
(2)如图1,连接BD交AC于点O,
因为四边形ABCD是正方形,∴O为AC的中点.
∵在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,
∴当M为SA的中点时,有BM=DM.∴OM⊥BD.
又∵四边形ABCD是正方形,∴AO⊥BD.
∴∠AOM即为平面BMD与平面ABCD所成的二面角的平面角.
又∵O为AC的中点,M为SA的中点,∴OM∥SC,且OM=SC=.
易得AM=,AO=1,∴cos ∠AOM==.
∴平面BMD与平面ABCD所成的二面角的余弦值为.
(3)在侧棱SC上存在点E,使得BE∥平面PAC,满足=2,理由如下:
取SD的中点Q,由SP=3PD,得PQ=PD,
如图2,过点Q作PC的平行线交SC于点E,连接BQ,BE,在△BDQ中,有BQ∥OP,∵PO 平面PAC,BQ 平面PAC,∴BQ∥平面PAC.
由=2,得==2,∴QE∥PC.
∵PC 平面PAC,QE 平面PAC,∴QE∥平面PAC.
∵BQ∩QE=Q,BQ,QE 平面BEQ,∴平面BEQ∥平面PAC.
∵BE 平面BEQ,∴BE∥平面PAC.
章末检测
(时间:120分钟,满分150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线l与平面α不平行,则( )
A.l与α相交 B.l α
C.l与α相交或l α D.以上结论都不对
2.(2024年封开月考)某圆锥母线长为1,其侧面积与轴截面面积的比值为2π,则该圆锥体积为( )
A. B.
C. D.
3.(2024年平果模拟)如图,一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形,已知直观图OA′B′C′中,B′C′=1,OC′=,则该平面图形的面积为( )
A. B.2
C.2 D.4
4.如图,正四棱锥P-ABCD的体积为2,底面积为6,E为侧棱PC的中点,则直线BE与平面PAC所成的角为( )
A.30° B.45°
C.60° D.90°
5.(2024年扬州模拟)已知某圆锥底面半径为1,高为2,则该圆锥的外接球表面积为( )
A.π B.π
C.π D.π
6.(2024年石家庄月考)已知m,n是两条不同的直线,α,β是两个不同的平面,则m∥α的一个充分条件是( )
A.m∥n,n∥α B.m∥β,α∥β
C.m⊥n,n⊥α,m α D.m∩n=A,n∥α,m α
7.(2024年临汾模拟)宋代是中国瓷器的黄金时代,涌现出了五大名窑:汝窑、官窑、哥窑、钧窑、定窑.其中汝窑被认为是五大名窑之首.如图1,这是汝窑双耳罐,该汝窑双耳罐可近似看成由两个圆台拼接而成,其直观图如图2所示.已知该汝窑双耳罐下底面圆的直径是12厘米,中间圆的直径是20厘米,上底面圆的直径是8厘米,高是14厘米,且上、下两圆台的高之比是3∶4,则该汝窑双耳罐的体积是( )
A.立方厘米 B.立方厘米
C.立方厘米 D.立方厘米
8.如图,在矩形ABCD中,AB=4,AD=2,P为边AB的中点,现将△DAP绕直线DP翻转至△DA′P处,若M为线段A′C的中点,则异面直线BM与PA′所成角的正切值为( )
A.4 B.2
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错的得0分.
9.(2024年深圳福田区模拟)如图,在正方体ABCD-A1B1C1D1中,直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,则直线l,m,n的位置关系可能是( )
A.l,m,n两两垂直 B.l,m,n两两平行
C.l,m,n两两相交 D.l,m,n两两异面
10.(2024年江门蓬江区月考)下列命题中正确的有( )
A.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为16π
B.圆柱形容器底半径为5 cm,两直径为5 cm的玻璃球都浸没在容器的水中,若取出这两个小球,则容器内水面下降的高度为 cm
C.正四棱台的上、下底面边长分别为2,4,侧棱长为2,其体积为
D.已知圆锥的母线长为10,侧面展开图的圆心角为,则该圆锥的体积为π
11.(2024年紫金期中)如图,在底面为等边三角形的直三棱柱ABC-A1B1C1中,AC=2,BB1=,D,E分别为棱BC,BB1的中点,则( )
A.A1B∥平面ADC1
B.AD⊥C1D
C.异面直线AC与DE所成角的余弦值为
D.平面ADC1与平面ABC的夹角的正切值为
三、填空题:本题共3小题,每小题5分,共15分.
12.(2024年聊城期中)五棱台的顶点数为V,棱数为E,面数为F,则V+F-E=________.
13.(2024年中山月考)已知球O是某圆锥内可放入的最大的球,其半径为该圆锥底面半径的一半,则该圆锥的体积与球O的体积的比值为________.
14.(2024年佛山高明区月考)某同学将一张圆心角为的扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,已知OB=2OA=60 cm,则制成的简易笔筒的体积为________cm3.
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图,平面ABEF⊥平面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC綉AD,BE綉FA,G,H分别为FA,FD的中点.
(1)求证:四边形BCHG是平行四边形;
(2)C,D,F,E四点是否共面?请说明理由.
16.(15分)(2024年封丘月考)如图,在正方体A1B1C1D1-ABCD中,E是DD1的中点.
(1)求证:D1B∥平面ACE;
(2)设正方体的棱长为1,求三棱锥B-AEC的体积.
17.(15分)如图,在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连接ED,EC,EB和DB.(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.
18.(17分)(2024年江门新会区月考)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=2,O是AC与BD的交点,PO⊥平面ABCD,PO=2,M是PD的中点.
(1)求证:PB∥平面ACM;
(2)求证:平面PBC⊥平面PAC;
(3)求直线AM与平面ABCD所成角的正切值.
19.(17分)(2024年深圳中学月考)如图,在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,P为侧棱SD上的点,且SP=3PD.
(1)求正四棱锥S-ABCD的表面积.
(2)若M为SA的中点,求平面BMD与平面ABCD所成的二面角的余弦值.
(3)侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求的值;若不存在,试说明理由.
参考答案
选择题
1.【答案】C
【解析】直线与平面的位置关系有:直线在平面内、直线与平面平行、直线与平面相交.因为直线l与平面α不平行,所以l与α相交或l α.
2.【答案】B
【解析】设该圆锥的底面半径为r,高h==,由侧面积与轴截面面积的比值为2π,可得=2π,解得r=,h==,则该圆锥的体积V圆锥=π××=.故选B.
3.【答案】D
【解析】因为直观图是底角为45°的等腰梯形,且B′C′=1,OC′=,所以等腰梯形的高h=OC′sin 45°=×=1,所以等腰梯形的面积S′=×(1+1+1+1)×1=2,所以原平面图形的面积S=2S′=2×2=4.故选D.
4.【答案】C
【解析】如图,在正四棱锥P-ABCD中,根据底面积为6,可得BC=.连接BD交AC于点O,连接PO,OE,则PO为正四棱锥P-ABCD的高,根据体积公式可得PO=1.因为PO⊥底面ABCD,所以PO⊥BD.又因为BD⊥AC,PO∩AC=O,所以BD⊥平面PAC.连接EO,则∠BEO为直线BE与平面PAC所成的角.在Rt△POA中,因为PO=1,OA=,所以PA=2,OE=PA=1.在Rt△BOE中,因为BO=,所以tan ∠BEO==,即∠BEO=60°.故直线BE与平面PAC所成角为60°.
5.【答案】C
【解析】根据题意,设圆锥外接球的半径为r,则有r2=1+(2-r)2,解得r=,则该圆锥的外接球表面积S=4πr2=.故选C.
6.【答案】C
【解析】对于A,由m∥n,n∥α,可得m α或m∥α,故A错误;对于B,由m∥β,α∥β,可得m α或m∥α,故B错误;对于C,由m⊥n,n⊥α,m α,可得m∥α,故C正确;对于D,由m∩n=A,n∥α,m α,可得m,α相交或m∥α,故D错误.故选C.
7.【答案】D
【解析】∵上、下两圆台的高之比是3∶4,∴上圆台的高为14×=6厘米,下圆台的高为14×=8厘米,故上圆台的体积为V1=6×=312π 立方厘米,下圆台的体积为V2=8×=π 立方厘米,故该汝窑双耳罐的体积为V1+V2=312π+π=立方厘米.故选D.
8.【答案】D
【解析】如图,取A′D的中点N,连接PN,MN.∵M是A′C的中点,∴MN∥CD,且MN=CD.∵四边形ABCD是矩形,P是AB的中点,∴PB∥CD,且PB=CD.∴MN∥PB,且MN=PB.∴四边形PBMN为平行四边形.∴MB∥PN.∴∠A′PN(或其补角)是异面直线BM与PA′所成的角.在Rt△A′PN中,tan ∠A′PN==,∴异面直线BM与PA′所成角的正切值为.故选D.
多项选择题
9.【答案】ACD
【解析】如图,当l为BB1,m为BC,n为CD时,满足直线l 平面ABB1A1,直线m 平面BCC1B1,直线n 平面ABCD,l,m,n两两相交且垂直,当l为A1B,m为B1C1,n为AC时,三条直线两两异面,故A,C,D正确;三条直线不可能两两平行,若l∥n,则l∥AB∥n,而AB与平面BCC1B1相交,则AB与m不平行,故B错误.故选ACD.
10.【答案】BCD
【解析】对于A,截面小圆半径为1,则球的半径R==,该球的表面积为4πR2=8π,A错误;对于B,设容器内水面下降的高度为h,则52π·h=2××3,解得h=,B正确;对于C,正四棱台的高h′==,体积为(22++42)×=,C正确;对于D,设圆锥的底面圆半径r,则2πr=10×,解得r=4,圆锥的高h0==2,体积为π×42×2=π,D正确.故选BCD.
11.【答案】ABD
【解析】如图,对于A,连接A1C交AC1于F,连接DF,则DF∥A1B,因为A1B 平面ADC1,DF 平面ADC1,所以A1B∥平面ADC1,故A正确;对于B,由题可知AD⊥BC,因为平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,所以AD⊥平面BCC1B1,又C1D 平面BCC1B1,所以AD⊥C1D,故B正确;对于C,连接CB1,AB1,则CB1∥DE,∠ACB1为异面直线AC与DE所成的角(或其补角),由余弦定理可得cos ∠ACB1===,故异面直线AC与DE所成角的余弦值为,故C错误;对于D,由B的分析过程可知∠CDC1为平面ADC1与平面ABC的夹角的平面角,所以tan ∠CDC1==,故D正确.故选ABD.
填空题
12.【答案】2
【解析】根据题意,在五棱台中,V=10,E=15,F=7,则V+F-E=2.
13.【答案】
【解析】设球的半径为r,则圆锥的底面圆的半径为2r,设O与圆锥底面圆的连线与圆锥底面所成的角为θ,则母线与底面所成角为2θ,则tan θ=,∴tan 2θ==,∴圆锥的高为2r tan 2θ=,∴该圆锥的体积与球O的体积的比值为=.
14.【答案】
【解析】根据题意,设所得圆台的上底半径为r1,下底半径为r2,在图1的扇形中,OB=60 cm,OA=30 cm,圆心角为,则有=2πr1=OA×=10π,变形可得r1=5 cm,同理,=2πr2=OB×=20π,变形可得r2=10 cm,AB=OB-OA=30 cm,则圆台的高h===5 cm,故圆台的体积V=(100π+25π+)×5= cm3.
解答题
15.(1)证明:由题设知,FG=GA,FH=HD,所以GH綉AD.
又因为BC綉AD,所以GH綉BC.所以四边形BCHG是平行四边形.
(2)解:C,D,F,E四点共面.理由如下.
由BE綉FA,G是FA的中点,知BE綉GF.
所以EF綉BG.由(1)知BG∥CH,所以EF∥CH.故EC,FH共面.
又因为点D在直线FH上,所以C,D,F,E四点共面.
16.(1)证明:如图,连接BD交AC于点O,连接OE,
则O为BD的中点,又因为E是DD1的中点,
所以OE是△BDD1的中位线,所以OE∥D1B,
又因为OE 平面AEC,D1B 平面AEC,所以D1B∥平面AEC;
(2)解:正方体ABCD-A1B1C1D1中,易知D1D⊥平面ABCD,所以
V三棱锥B-AEC=V三棱锥E-ABC=S△ABC·ED=××AB×BC×ED=××1×1×=.
17.(1)证明:由题意可知△DD1E为等腰直角三角形,∠D1ED=45°.
同理,∠C1EC=45°.所以∠DEC=90°,即DE⊥EC.
又因为BC⊥平面D1DCC1,DE 平面D1DCC1,所以BC⊥DE.
又因为EC∩BC=C,所以DE⊥平面EBC.
因为DE 平面EDB,所以平面EDB⊥平面EBC.
(2)解:如图,过E作EO⊥DC于点O,过点O作OF⊥DB于点F,连接EF.
因为平面ABCD⊥平面D1DCC1,且交线为DC,
所以EO⊥平面ABCD,所以EO⊥OF,EO⊥BD.
由BD⊥OF,BD⊥OE,OF∩OE=O,得BD⊥平面EFO,所以BD⊥EF.
所以∠EFO为二面角E-DB-C的平面角.
在Rt△EFO中,易求得OF=,又因为OE=1,所以tan ∠EFO==.
所以二面角E-DB-C的正切值为.
18.(1)证明:在平行四边形ABCD中,∵O为AC与BD的交点,
∴O为BD的中点,又M为PD的中点,∴PB∥MO.
又∵PB 平面ACM,MO 平面ACM,∴PB∥平面ACM.
(2)证明:∵PO⊥平面ABCD,BC 平面ABCD,∴BC⊥PO.
在△ADC中,∵AD=AC,∴AD⊥AC.∵AD∥BC,∴BC⊥AC.
∵PO∩AC=O,PO 平面PAC,AC 平面PAC,∴BC⊥平面PAC.
又∵BC 平面PBC,∴平面PBC⊥平面PAC.
(3)解:如图,取DO的中点N,连接MN,AN,∵M为PD的中点,
∴MN∥PO,且MN=PO=1.
由PO⊥平面ABCD,得MN⊥平面ABCD,∴∠MAN是直线AM与平面ABCD所成的角.
∵∠ADC=45°,AD=AC=2,∠ACD=∠ADC=45°,∴∠CAD=90°.
在Rt△DAO中,AD=2,AO=AC=1,∴DO=,从而AN=DO=.在Rt△ANM中,tan ∠MAN===,∴直线AM与平面ABCD所成角的正切值为.
19.解:(1)在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,
则正四棱锥侧面的高为h==,
∴正四棱锥的表面积为S=4×××+×=8.
(2)如图1,连接BD交AC于点O,
因为四边形ABCD是正方形,∴O为AC的中点.
∵在正四棱锥S-ABCD中,SA=SB=SC=SD=,AB=,
∴当M为SA的中点时,有BM=DM.∴OM⊥BD.
又∵四边形ABCD是正方形,∴AO⊥BD.
∴∠AOM即为平面BMD与平面ABCD所成的二面角的平面角.
又∵O为AC的中点,M为SA的中点,∴OM∥SC,且OM=SC=.
易得AM=,AO=1,∴cos ∠AOM==.
∴平面BMD与平面ABCD所成的二面角的余弦值为.
(3)在侧棱SC上存在点E,使得BE∥平面PAC,满足=2,理由如下:
取SD的中点Q,由SP=3PD,得PQ=PD,
如图2,过点Q作PC的平行线交SC于点E,连接BQ,BE,在△BDQ中,有BQ∥OP,∵PO 平面PAC,BQ 平面PAC,∴BQ∥平面PAC.
由=2,得==2,∴QE∥PC.
∵PC 平面PAC,QE 平面PAC,∴QE∥平面PAC.
∵BQ∩QE=Q,BQ,QE 平面BEQ,∴平面BEQ∥平面PAC.
∵BE 平面BEQ,∴BE∥平面PAC.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
