第五章 基本平面图形 3 多边形和圆的初步认识 教案(表格式)
文档属性
| 名称 | 第五章 基本平面图形 3 多边形和圆的初步认识 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 87.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 16:42:54 | ||
图片预览

文档简介
第五章 基本平面图形
课表摘录
1.通过实物和模型,了解从物体抽象出来的直线的概念.
2. 会比较线段的长短,理解线段的和、差,以及线段中点的意义.
3. 掌握基本事实:两点确定一条直线.
4. 掌握基本事实:两点之间线段最短.
5.理解两点间距离的意义,能度量和表达两点间的距离.
6. 理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
7. 能用尺规作图:作一个角等于已知角,作一条线段等于已知线段.
8. 了解多边形的概念及多边形的顶点、边、内角与对角线.
9.了解正多边形的概念.
10.理解圆、弧、圆心角的概念.
11.会计算扇形的面积.
教材分析
本章主要内容是研究基本平面图形的概念及性质.主要内容包括: 直线、射线、线段的概念、表示方法和它们的联系与区别;关于直线和线段的基本事实;两点之间距离的意义;比较线段的长短的方法; 线段的和、差及线段的中点概念;会画一条线段等于已知线段;角的两种描述方法及表示方法;认识度、分、秒,并会进行简单的换算;会比较角的大小及计算角度的和差;角平分线、多边形及圆的有关概念.
教学目标
1.认识线段、射线、直线、角、多边形、扇形、圆等简单平面图形,进一步了解其含义和相关性质.
2.能够熟练用符号表示线段、射线、直线、角.
3.会进行线段长短或角的大小的比较,能估计一个角的大小,会进行角的单位的简单换算.
教学重难点
重点:应用图形与几何的知识解释生活中的现象以及解决简单的实际问题.
难点:形成初步完整的几何概念,丰富学生对基本几何图形概念的认识.
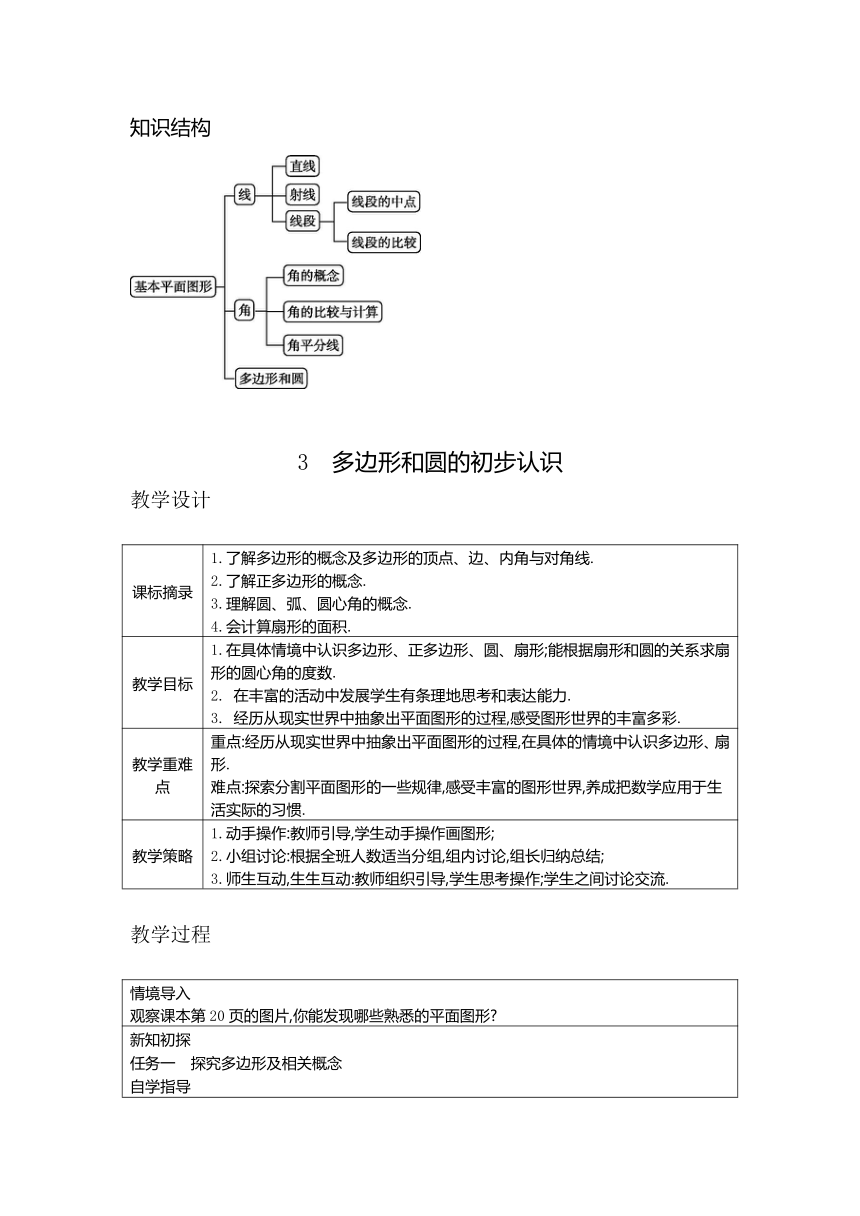
知识结构
3 多边形和圆的初步认识
教学设计
课标摘录 1.了解多边形的概念及多边形的顶点、边、内角与对角线. 2.了解正多边形的概念. 3.理解圆、弧、圆心角的概念. 4.会计算扇形的面积.
教学目标 1.在具体情境中认识多边形、正多边形、圆、扇形;能根据扇形和圆的关系求扇形的圆心角的度数. 2. 在丰富的活动中发展学生有条理地思考和表达能力. 3. 经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩.
教学重难点 重点:经历从现实世界中抽象出平面图形的过程,在具体的情境中认识多边形、扇形. 难点:探索分割平面图形的一些规律,感受丰富的图形世界,养成把数学应用于生活实际的习惯.
教学策略 1.动手操作:教师引导,学生动手操作画图形; 2.小组讨论:根据全班人数适当分组,组内讨论,组长归纳总结; 3.师生互动,生生互动:教师组织引导,学生思考操作;学生之间讨论交流.
教学过程
情境导入 观察课本第20页的图片,你能发现哪些熟悉的平面图形
新知初探 任务一 探究多边形及相关概念 自学指导 如图,仔细观察并回答问题. (1)什么是多边形 由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形. (2)我们常见的图形哪些是多边形 三角形、四边形、五边形、六边形等. (3)四边形、五边形、六边形的对角线是怎么定义的 你能给出多边形对角线的定义吗 在多边形中,连接不相邻两个顶点的线段叫作多边形的对角线. (4)找出图中多边形的顶点、边、内角以及对角线.
顶点:点A、点B、点C、点D、点E; 边:线段AB、线段BC、线段CD、线段DE、线段EA; 内角:∠ABC,∠BCD,∠CDE,∠DEA,∠EAB; 对角线:线段AC、线段AD. (5)你还能画出图中的其他对角线吗 线段BE、线段BD、线段CE. 合作探究 1.思考: (1)n边形有多少个顶点、多少条边、多少个内角 n个顶点,n条边,n个内角. (2)过n边形的一个顶点有几条对角线 过n边形的一个顶点有(n-3)条对角线. 2.观察下图中的多边形,它们的边、角有什么特点 归纳:各边相等、各角也相等的多边形叫作正多边形. 图中各多边形的名称为:正三角形、正四边形(正方形)、正五边形、正六边形、正八边形. 例1 若一个多边形从一个顶点出发最多可以引10条对角线,则它是( A ) A.十三边形 B.十二边形 C.十一边形 D.十边形 【即时测评】判断: (1)所有边长都相等的多边形叫作正多边形.( × ) (2)所有角的度数都相等的多边形叫作正多边形.( × ) 任务一 意图说明 通过类比探究,得出多边形的相关概念,通过例题和练习进一步巩固对概念的理解,并会在解题中运用. 任务二 探究圆的相关概念 阅读课本第21页“观察·思考”的内容,回答以下问题: (1)你还记得用哪些方法可以画一个圆吗 什么样的图形叫作圆 平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫作圆. (2)找出图中的半径、圆弧、扇形和圆心角. 半径AO,BO;;扇形AOB;圆心角∠AOB. (3)怎样读写圆弧 写作:,读作:圆弧AB或者弧AB. 例2 将一个圆分割成三个扇形,它们的圆心角的度数比为1∶2∶3,求这三个扇形的圆心角的度数. 解:因为周角的度数是360°, 所以分成的三个扇形的圆心角分别为: 360°×=60°,360°×=120°,360°×=180°. 设计意图:巩固对圆的相关概念——圆心角的理解.
例3 如图是一个圆,将它分割成四个扇形,使它们的圆心角的度数比为2∶3∶4∶3. (1)求这四个扇形的圆心角的度数,并画出四个扇形; (2)若圆的半径为2 cm,请求出这四个扇形的面积. 解:(1)如图. 因为一个圆被分割成四个扇形,它们的圆心角的度数比为2∶3∶4∶3, 所以它们对应的圆心角分别为:360°×=60°,360°×=90°,360°×=120°,360°×=90°. (2)因为圆的半径为2 cm, 所以S1==π(cm2),S2==π(cm2),S3==π(cm2),S4==π(cm2). 任务二 意图说明 通过图形认识和计算,对圆有进一步认识.
当堂达标 见导学案(或课件)
课堂小结 1.多边形是怎样定义的 2.多边形对角线的定义是什么 过n边形的每个顶点有几条对角线 3.正多边形有哪些特点 4.怎样求扇形的圆心角及面积
板书设计 多边形和圆的初步认识 1.多边形的定义 2.多边形的对角线 3.正多边形的定义 4.圆、圆弧、扇形、圆心角 例1 例2 例3
教学反思 本节课概念较多,主要通过类比学习得出相应的概念,渗透了类比的数学思想,在教学中注重让学生主动参与学习活动,观察感受,亲身经历探究的过程,通过自主、合作感悟知识的生成、变化、发展,激发学生的联想与再创造能力.
课表摘录
1.通过实物和模型,了解从物体抽象出来的直线的概念.
2. 会比较线段的长短,理解线段的和、差,以及线段中点的意义.
3. 掌握基本事实:两点确定一条直线.
4. 掌握基本事实:两点之间线段最短.
5.理解两点间距离的意义,能度量和表达两点间的距离.
6. 理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
7. 能用尺规作图:作一个角等于已知角,作一条线段等于已知线段.
8. 了解多边形的概念及多边形的顶点、边、内角与对角线.
9.了解正多边形的概念.
10.理解圆、弧、圆心角的概念.
11.会计算扇形的面积.
教材分析
本章主要内容是研究基本平面图形的概念及性质.主要内容包括: 直线、射线、线段的概念、表示方法和它们的联系与区别;关于直线和线段的基本事实;两点之间距离的意义;比较线段的长短的方法; 线段的和、差及线段的中点概念;会画一条线段等于已知线段;角的两种描述方法及表示方法;认识度、分、秒,并会进行简单的换算;会比较角的大小及计算角度的和差;角平分线、多边形及圆的有关概念.
教学目标
1.认识线段、射线、直线、角、多边形、扇形、圆等简单平面图形,进一步了解其含义和相关性质.
2.能够熟练用符号表示线段、射线、直线、角.
3.会进行线段长短或角的大小的比较,能估计一个角的大小,会进行角的单位的简单换算.
教学重难点
重点:应用图形与几何的知识解释生活中的现象以及解决简单的实际问题.
难点:形成初步完整的几何概念,丰富学生对基本几何图形概念的认识.
知识结构
3 多边形和圆的初步认识
教学设计
课标摘录 1.了解多边形的概念及多边形的顶点、边、内角与对角线. 2.了解正多边形的概念. 3.理解圆、弧、圆心角的概念. 4.会计算扇形的面积.
教学目标 1.在具体情境中认识多边形、正多边形、圆、扇形;能根据扇形和圆的关系求扇形的圆心角的度数. 2. 在丰富的活动中发展学生有条理地思考和表达能力. 3. 经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩.
教学重难点 重点:经历从现实世界中抽象出平面图形的过程,在具体的情境中认识多边形、扇形. 难点:探索分割平面图形的一些规律,感受丰富的图形世界,养成把数学应用于生活实际的习惯.
教学策略 1.动手操作:教师引导,学生动手操作画图形; 2.小组讨论:根据全班人数适当分组,组内讨论,组长归纳总结; 3.师生互动,生生互动:教师组织引导,学生思考操作;学生之间讨论交流.
教学过程
情境导入 观察课本第20页的图片,你能发现哪些熟悉的平面图形
新知初探 任务一 探究多边形及相关概念 自学指导 如图,仔细观察并回答问题. (1)什么是多边形 由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形. (2)我们常见的图形哪些是多边形 三角形、四边形、五边形、六边形等. (3)四边形、五边形、六边形的对角线是怎么定义的 你能给出多边形对角线的定义吗 在多边形中,连接不相邻两个顶点的线段叫作多边形的对角线. (4)找出图中多边形的顶点、边、内角以及对角线.
顶点:点A、点B、点C、点D、点E; 边:线段AB、线段BC、线段CD、线段DE、线段EA; 内角:∠ABC,∠BCD,∠CDE,∠DEA,∠EAB; 对角线:线段AC、线段AD. (5)你还能画出图中的其他对角线吗 线段BE、线段BD、线段CE. 合作探究 1.思考: (1)n边形有多少个顶点、多少条边、多少个内角 n个顶点,n条边,n个内角. (2)过n边形的一个顶点有几条对角线 过n边形的一个顶点有(n-3)条对角线. 2.观察下图中的多边形,它们的边、角有什么特点 归纳:各边相等、各角也相等的多边形叫作正多边形. 图中各多边形的名称为:正三角形、正四边形(正方形)、正五边形、正六边形、正八边形. 例1 若一个多边形从一个顶点出发最多可以引10条对角线,则它是( A ) A.十三边形 B.十二边形 C.十一边形 D.十边形 【即时测评】判断: (1)所有边长都相等的多边形叫作正多边形.( × ) (2)所有角的度数都相等的多边形叫作正多边形.( × ) 任务一 意图说明 通过类比探究,得出多边形的相关概念,通过例题和练习进一步巩固对概念的理解,并会在解题中运用. 任务二 探究圆的相关概念 阅读课本第21页“观察·思考”的内容,回答以下问题: (1)你还记得用哪些方法可以画一个圆吗 什么样的图形叫作圆 平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫作圆. (2)找出图中的半径、圆弧、扇形和圆心角. 半径AO,BO;;扇形AOB;圆心角∠AOB. (3)怎样读写圆弧 写作:,读作:圆弧AB或者弧AB. 例2 将一个圆分割成三个扇形,它们的圆心角的度数比为1∶2∶3,求这三个扇形的圆心角的度数. 解:因为周角的度数是360°, 所以分成的三个扇形的圆心角分别为: 360°×=60°,360°×=120°,360°×=180°. 设计意图:巩固对圆的相关概念——圆心角的理解.
例3 如图是一个圆,将它分割成四个扇形,使它们的圆心角的度数比为2∶3∶4∶3. (1)求这四个扇形的圆心角的度数,并画出四个扇形; (2)若圆的半径为2 cm,请求出这四个扇形的面积. 解:(1)如图. 因为一个圆被分割成四个扇形,它们的圆心角的度数比为2∶3∶4∶3, 所以它们对应的圆心角分别为:360°×=60°,360°×=90°,360°×=120°,360°×=90°. (2)因为圆的半径为2 cm, 所以S1==π(cm2),S2==π(cm2),S3==π(cm2),S4==π(cm2). 任务二 意图说明 通过图形认识和计算,对圆有进一步认识.
当堂达标 见导学案(或课件)
课堂小结 1.多边形是怎样定义的 2.多边形对角线的定义是什么 过n边形的每个顶点有几条对角线 3.正多边形有哪些特点 4.怎样求扇形的圆心角及面积
板书设计 多边形和圆的初步认识 1.多边形的定义 2.多边形的对角线 3.正多边形的定义 4.圆、圆弧、扇形、圆心角 例1 例2 例3
教学反思 本节课概念较多,主要通过类比学习得出相应的概念,渗透了类比的数学思想,在教学中注重让学生主动参与学习活动,观察感受,亲身经历探究的过程,通过自主、合作感悟知识的生成、变化、发展,激发学生的联想与再创造能力.
同课章节目录
