第四单元第8讲 最大公因数的实际应用 (讲义)(含答案)-五年级数学下册同步知识点讲练(人教版)
文档属性
| 名称 | 第四单元第8讲 最大公因数的实际应用 (讲义)(含答案)-五年级数学下册同步知识点讲练(人教版) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览




文档简介
五年级数学下册同步知识点讲练
第四单元第8讲:最大公因数的实际应用
知识点 ① 运用公因数和最大公因数解决问题
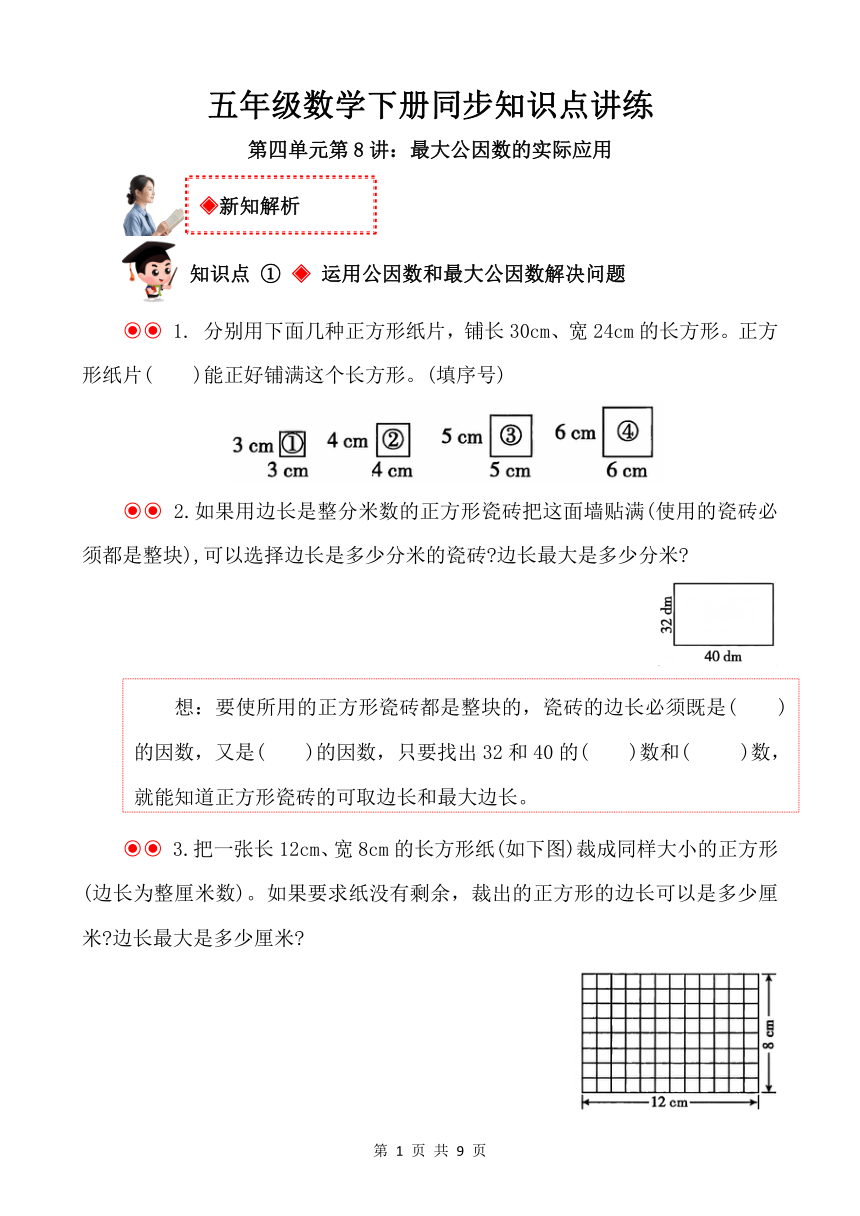
1. 分别用下面几种正方形纸片,铺长30cm、宽24cm的长方形。正方形纸片( )能正好铺满这个长方形。(填序号)
2.如果用边长是整分米数的正方形瓷砖把这面墙贴满(使用的瓷砖必须都是整块),可以选择边长是多少分米的瓷砖 边长最大是多少分米
3.把一张长12cm、宽8cm的长方形纸(如下图)裁成同样大小的正方形(边长为整厘米数)。如果要求纸没有剩余,裁出的正方形的边长可以是多少厘米 边长最大是多少厘米
【答案】:
1. ①④
【点拨】要使正方形纸片能正好铺满长方形,则正方形纸片的边长必须同时是长方形的长和宽的因数。
2. 32 40 公因 最大公因
32的因数:1,2,4,8,16,32。
40的因数:1,2,4,5,8,10,20,40。
32和40的公因数:1,2,4,8。
答:可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最大是8dm。
3. 裁出的正方形的边长可以是1cm,2cm或4cm。边长最大是4cm。
【点拨】要使裁成同样大小的正方形,且没有剩余,正方形的边长必须是12的因数,又是8的因数。因此找出12和8的公因数和最大公因数,就能知道裁成的正方形的边长可取的值和边长最大值。
1.填空题
(1)用边长是整厘米的正方形铺满长18cm、宽12cm的长方形,能正好铺满的正方形边长可以是( )cm,最大边长是( )cm。
(2)要铺一个长45dm、宽30dm的地面,选择的正方形瓷砖边长必须既是45的( ),又是30的( ),最大边长是( )dm。
(3)把长24cm和宽16cm的彩纸裁成相同大小的正方形(无剩余),边长最大是( )cm,此时能裁出( )块。
2.选择题。
(1)用边长整分米的正方形瓷砖铺长20dm、宽15dm的墙面,不可选的边长是( )。
A. 1dm B. 3dm C. 5dm D. 6dm
(2)若两个数的最大公因数是6,则它们可能是( )。
A. 12和18 B. 8和10 C. 6和9 D. 15和20
(3)用边长整米的地砖铺长9m、宽6m的走廊,最大可选边长是( )。
A. 1m B. 3m C. 6m D. 9m
3.判断题。
(1)边长4cm的正方形能铺满长16cm、宽12cm的长方形。( )
(2)两个数的最大公因数一定比这两个数都小。( )
(3)若两个数的公因数只有1,则它们的最大公因数是它们的最小公倍数。( )
知识点② 运用三个数的最大公因数解决问题
有三根钢丝,长度分别是12m、18m和30m,现在要把它们截成长度相同的小段,且每一根都不能有剩余,每段最长是多少米 一共可以截成多少段
【答案】:
12的因数:1,2,3,4,6,12。
18的因数:1,2,3,6,9,18。
30的因数:1,2,3,5,6,10,15,30。
12,18和30的最大公因数是6。
12÷6+18÷6+30÷6=10(段)
答:每段最长是6m,一共可以截成10段。
【点拨】要把三根钢丝截成长度相同的小段,且不能有剩余,则每段的长度应同时是12,18和30的因数,求每段最长是多少米,就是求12,18和30的最大公因数。钢丝总长÷每段的长度=段数,求出三根钢丝分别能截多少段,最后求和。
1.幼儿园老师要把24个苹果、36个橘子和48个草莓,平均分给小朋友们,要使每个小朋友分得的三种水果数量一样且水果无剩余,最多可以分给几个小朋友?每个小朋友能分到几种水果,分别是多少个?
2.有三根木棒,长度分别是20厘米、30厘米和45厘米,现在要把它们锯成同样长的小段且没有剩余,每小段最长是多少厘米?一共能锯成多少段?
3.手工课上,老师准备了40张红纸、56张黄纸和72张蓝纸,要把这些纸裁成大小相同的正方形且没有剩余,裁出的正方形边长最大是多少厘米(假设纸张边长为整厘米数)?三种颜色的纸分别能裁出多少个正方形?
知识点③ 用“转化法”解决问题
妈妈买回一条50dm长的红丝带和一条43dm长的蓝丝带。妈妈要把它们剪成同样长的小段,结果红丝带余2dm,蓝丝带余3dm。所剪成的小段最长是多少分米
【答案】:
50-2=48(dm);43-3=40(dm)
48和40的最大公因数是8。
答:所剪成的小段最长是8dm。
【点拨】剪成同样长的小段后,红丝带和蓝丝带都有剩余,则实际所用的丝带长度=丝带总长-剩余的丝带长度。因此红丝带实际用了50-2=48(dm),蓝丝带实际用了43-3=40(dm)。求所剪成的小段最长是多少分米,就是求48和40的最大公因数。
1.小明有两根绳子,一根长72分米,另一根长56分米。他想将这两根绳子剪成同样长的小段,结果第一根绳子余下2分米,第二根绳子余下6分米。所剪成的小段最长是多少分米?
2.服装厂有两块布料,一块长85米,另一块长68米。需要将它们裁成相同长度的布条,第一块布料余下5米,第二块布料余下8米。每条布条的最大可能长度是多少米?
3.学校图书馆新进一批图书,甲类书有96本,乙类书有60本。管理员想将它们分装到同样大小的盒子中,甲类书最后剩下6本,乙类书剩下12本。每个盒子最多能装多少本书?
有一块长方形草坪,长60m,宽48m。要在它的四周和四个角栽上树苗,每相邻两棵树苗之间的距离相等。每相邻两棵树苗之间的距离最大是多少米 此时一共可以栽多少棵树苗
当所求量分别与两个已知量的因数有关时,可以用公因数和最大公因数的知识解决。
参考答案
1.填空题
(1)1、2、3、6 6
(2)因数 因数 15
(3)8 6
2.选择题。
(1)D (2)A (3)B
3.判断题
(1)√ (2)× (3)×
1.先求24、36和48的最大公因数,24=2×2×2×3,36=2×2×3×3,48=2×2×2×2×3,最大公因数是2×2×3=12,所以最多可以分给12个小朋友。
每个小朋友分到苹果:24÷12=2(个);
橘子:36÷12=3(个);
草莓:48÷12=4(个)。
2.对20、30和45分解质因数,20=2×2×5,30=2×3×5,45=3×3×5,最大公因数是5,即每小段最长是5厘米。
20÷5+30÷5+45÷5=4+6+9=19(段),
一共能锯成19段。
3.分解质因数,40=2×2×2×5,56=2×2×2×7,72=2×2×2×3×3,最大公因数是2×2×2=8,所以裁出的正方形边长最大是8厘米。
红纸能裁出:40÷8=5(个);
黄纸能裁出:56÷8=7(个);
蓝纸能裁出:72÷8=9(个)。
1.总长度减去余数,转化为求最大公因数。
第一根实际剪去的长度:72-2=70dm
第二根实际剪去的长度:56-6=50dm
求70和50的最大公因数:公因数有1,2,5,10,最大为10。
答案:最长小段是10分米。
2.总长度减去余数后求最大公因数。
第一块实际剪去的长度:85-5=80m
第二块实际剪去的长度:68-8=60m
求80和60的最大公因数:公因数有1,2,4,5,10,20,最大为20。
答案:每条布条最长是20米。
3.总本数减去余数后求最大公因数。
甲类书实际装入盒子的数量:96-6=90本
乙类书实际装入盒子的数量:60-12=48本
求90和48的最大公因数:公因数有1,2,3,6,最大为6。
答案:每个盒子最多装6本。
60和48的最大公因数是12。
(60+48)×2÷12=18(棵)
答:每相邻两棵树苗之间的距离最大是12m,此时一共可以栽18棵树苗。
【点拨】要求每相邻两棵树苗之间的最大距离,就是求60和48的最大公因数。因为长方形草坪四个角上也栽树苗,所以直接用长方形的周长÷每相邻两棵树苗之间的最大距离即可求出此时一共可以栽多少棵树苗
第四单元第8讲:最大公因数的实际应用
知识点 ① 运用公因数和最大公因数解决问题
1. 分别用下面几种正方形纸片,铺长30cm、宽24cm的长方形。正方形纸片( )能正好铺满这个长方形。(填序号)
2.如果用边长是整分米数的正方形瓷砖把这面墙贴满(使用的瓷砖必须都是整块),可以选择边长是多少分米的瓷砖 边长最大是多少分米
3.把一张长12cm、宽8cm的长方形纸(如下图)裁成同样大小的正方形(边长为整厘米数)。如果要求纸没有剩余,裁出的正方形的边长可以是多少厘米 边长最大是多少厘米
【答案】:
1. ①④
【点拨】要使正方形纸片能正好铺满长方形,则正方形纸片的边长必须同时是长方形的长和宽的因数。
2. 32 40 公因 最大公因
32的因数:1,2,4,8,16,32。
40的因数:1,2,4,5,8,10,20,40。
32和40的公因数:1,2,4,8。
答:可以选择边长是1dm,2dm,4dm,8dm的瓷砖,边长最大是8dm。
3. 裁出的正方形的边长可以是1cm,2cm或4cm。边长最大是4cm。
【点拨】要使裁成同样大小的正方形,且没有剩余,正方形的边长必须是12的因数,又是8的因数。因此找出12和8的公因数和最大公因数,就能知道裁成的正方形的边长可取的值和边长最大值。
1.填空题
(1)用边长是整厘米的正方形铺满长18cm、宽12cm的长方形,能正好铺满的正方形边长可以是( )cm,最大边长是( )cm。
(2)要铺一个长45dm、宽30dm的地面,选择的正方形瓷砖边长必须既是45的( ),又是30的( ),最大边长是( )dm。
(3)把长24cm和宽16cm的彩纸裁成相同大小的正方形(无剩余),边长最大是( )cm,此时能裁出( )块。
2.选择题。
(1)用边长整分米的正方形瓷砖铺长20dm、宽15dm的墙面,不可选的边长是( )。
A. 1dm B. 3dm C. 5dm D. 6dm
(2)若两个数的最大公因数是6,则它们可能是( )。
A. 12和18 B. 8和10 C. 6和9 D. 15和20
(3)用边长整米的地砖铺长9m、宽6m的走廊,最大可选边长是( )。
A. 1m B. 3m C. 6m D. 9m
3.判断题。
(1)边长4cm的正方形能铺满长16cm、宽12cm的长方形。( )
(2)两个数的最大公因数一定比这两个数都小。( )
(3)若两个数的公因数只有1,则它们的最大公因数是它们的最小公倍数。( )
知识点② 运用三个数的最大公因数解决问题
有三根钢丝,长度分别是12m、18m和30m,现在要把它们截成长度相同的小段,且每一根都不能有剩余,每段最长是多少米 一共可以截成多少段
【答案】:
12的因数:1,2,3,4,6,12。
18的因数:1,2,3,6,9,18。
30的因数:1,2,3,5,6,10,15,30。
12,18和30的最大公因数是6。
12÷6+18÷6+30÷6=10(段)
答:每段最长是6m,一共可以截成10段。
【点拨】要把三根钢丝截成长度相同的小段,且不能有剩余,则每段的长度应同时是12,18和30的因数,求每段最长是多少米,就是求12,18和30的最大公因数。钢丝总长÷每段的长度=段数,求出三根钢丝分别能截多少段,最后求和。
1.幼儿园老师要把24个苹果、36个橘子和48个草莓,平均分给小朋友们,要使每个小朋友分得的三种水果数量一样且水果无剩余,最多可以分给几个小朋友?每个小朋友能分到几种水果,分别是多少个?
2.有三根木棒,长度分别是20厘米、30厘米和45厘米,现在要把它们锯成同样长的小段且没有剩余,每小段最长是多少厘米?一共能锯成多少段?
3.手工课上,老师准备了40张红纸、56张黄纸和72张蓝纸,要把这些纸裁成大小相同的正方形且没有剩余,裁出的正方形边长最大是多少厘米(假设纸张边长为整厘米数)?三种颜色的纸分别能裁出多少个正方形?
知识点③ 用“转化法”解决问题
妈妈买回一条50dm长的红丝带和一条43dm长的蓝丝带。妈妈要把它们剪成同样长的小段,结果红丝带余2dm,蓝丝带余3dm。所剪成的小段最长是多少分米
【答案】:
50-2=48(dm);43-3=40(dm)
48和40的最大公因数是8。
答:所剪成的小段最长是8dm。
【点拨】剪成同样长的小段后,红丝带和蓝丝带都有剩余,则实际所用的丝带长度=丝带总长-剩余的丝带长度。因此红丝带实际用了50-2=48(dm),蓝丝带实际用了43-3=40(dm)。求所剪成的小段最长是多少分米,就是求48和40的最大公因数。
1.小明有两根绳子,一根长72分米,另一根长56分米。他想将这两根绳子剪成同样长的小段,结果第一根绳子余下2分米,第二根绳子余下6分米。所剪成的小段最长是多少分米?
2.服装厂有两块布料,一块长85米,另一块长68米。需要将它们裁成相同长度的布条,第一块布料余下5米,第二块布料余下8米。每条布条的最大可能长度是多少米?
3.学校图书馆新进一批图书,甲类书有96本,乙类书有60本。管理员想将它们分装到同样大小的盒子中,甲类书最后剩下6本,乙类书剩下12本。每个盒子最多能装多少本书?
有一块长方形草坪,长60m,宽48m。要在它的四周和四个角栽上树苗,每相邻两棵树苗之间的距离相等。每相邻两棵树苗之间的距离最大是多少米 此时一共可以栽多少棵树苗
当所求量分别与两个已知量的因数有关时,可以用公因数和最大公因数的知识解决。
参考答案
1.填空题
(1)1、2、3、6 6
(2)因数 因数 15
(3)8 6
2.选择题。
(1)D (2)A (3)B
3.判断题
(1)√ (2)× (3)×
1.先求24、36和48的最大公因数,24=2×2×2×3,36=2×2×3×3,48=2×2×2×2×3,最大公因数是2×2×3=12,所以最多可以分给12个小朋友。
每个小朋友分到苹果:24÷12=2(个);
橘子:36÷12=3(个);
草莓:48÷12=4(个)。
2.对20、30和45分解质因数,20=2×2×5,30=2×3×5,45=3×3×5,最大公因数是5,即每小段最长是5厘米。
20÷5+30÷5+45÷5=4+6+9=19(段),
一共能锯成19段。
3.分解质因数,40=2×2×2×5,56=2×2×2×7,72=2×2×2×3×3,最大公因数是2×2×2=8,所以裁出的正方形边长最大是8厘米。
红纸能裁出:40÷8=5(个);
黄纸能裁出:56÷8=7(个);
蓝纸能裁出:72÷8=9(个)。
1.总长度减去余数,转化为求最大公因数。
第一根实际剪去的长度:72-2=70dm
第二根实际剪去的长度:56-6=50dm
求70和50的最大公因数:公因数有1,2,5,10,最大为10。
答案:最长小段是10分米。
2.总长度减去余数后求最大公因数。
第一块实际剪去的长度:85-5=80m
第二块实际剪去的长度:68-8=60m
求80和60的最大公因数:公因数有1,2,4,5,10,20,最大为20。
答案:每条布条最长是20米。
3.总本数减去余数后求最大公因数。
甲类书实际装入盒子的数量:96-6=90本
乙类书实际装入盒子的数量:60-12=48本
求90和48的最大公因数:公因数有1,2,3,6,最大为6。
答案:每个盒子最多装6本。
60和48的最大公因数是12。
(60+48)×2÷12=18(棵)
答:每相邻两棵树苗之间的距离最大是12m,此时一共可以栽18棵树苗。
【点拨】要求每相邻两棵树苗之间的最大距离,就是求60和48的最大公因数。因为长方形草坪四个角上也栽树苗,所以直接用长方形的周长÷每相邻两棵树苗之间的最大距离即可求出此时一共可以栽多少棵树苗
