江苏省淮安市淮阴区2015-2016学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 江苏省淮安市淮阴区2015-2016学年高二下学期期中考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 103.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-13 00:00:00 | ||
图片预览


文档简介
2015—2016学年度第二学期期期中考试
高二文数学试题
时 间:120分钟 满 分:160分
一.填空题(每题5分,计70分)
1.已知全集,集合,,则 .
2.设,则 (用含的代数式表示)
3.已知复数满足,为虚数单位,则的值为 .
4.函数f(x)=2-3(a>0且a≠1)的图象经过的定点坐标是________.
5.函数在区间上是增函数,那么a的取值范围是 。
6.若,,,则a、b、c从小到大的顺序是 。
7.幂函数在上单调递增,则
8.设函数 若, 则a的取值范围是
9.f(x)是R上的奇函数,当x≥0时,f(x)=x3+ln(1+x),则当x<0时,f(x)= .
10.从,,,,…,推广到第个等式为_________________________.
11.已知是定义在R上的偶函数,并且,当时, 则
12.已知函数的值域为且在上是增函数,则的取值范围是 。
13.十六进制与十进制的对应如下表:
十六进制 1 2 3 4 5 6 7 8 9 10 A B C D E F
十进制 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
例如:A+B=11+12=16+7=F+7=17,所以A+B的值用十六进制表示就等于17。
试计算:A×B+D = (用十六进制表示)
14.已知,
且,则满足条件的所有整数的和是
二.解答题(计90分)
15.(本小题满分14分)已知函数的定义域为集合,函数
的值域为集合.
(1)求;
(2)若集合,且,求实数的取值范围.
16.(本小题满分14分)(1)已知,求实数的值;
(2)已知,若是纯虚数,求.
17.(本小题满分14分)已知函数 (a为常数).
(1)若常数a<2且a≠0,求f(x)的定义域;
(2)若f(x)在区间(2,4)上是减函数,求a的取值范围.
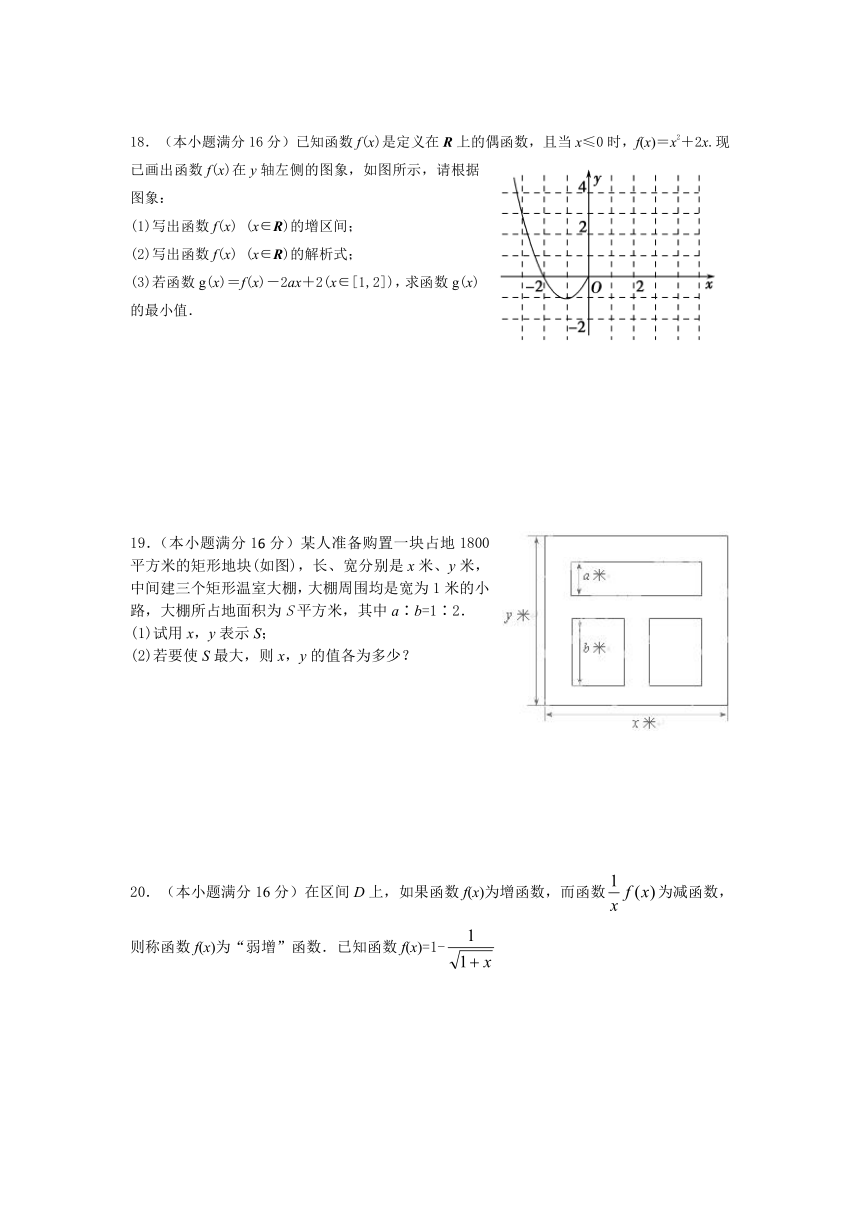
18.(本小题满分16分)已知函数f(x ( http: / / www.21cnjy.com ))是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
(1)写出函数f(x) (x∈R)的增区间;
(2)写出函数f(x) (x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
19.(本小题满分16分)某人准备购置一块 ( http: / / www.21cnjy.com )占地1800平方米的矩形地块(如图),长、宽分别是x米、y米,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路,大棚所占地面积为S平方米,其中a∶b=1∶2.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?
20.(本小题满分16分)在区间D上,如果函数f(x)为增函数,而函数为减函数,则称函数f(x)为“弱增”函数.已知函数f(x)=1-
(1)判断函数f(x)在区间(0,1]上是否为“弱增”函数;
(2)设,,证明:;
(3)当x∈[0,1]时,不等式1-ax≤≤1-bx恒成立,求实数a,b的取值范围.
2015—2016学年度第二学期期期中考试
高二文数学试题答案
一.填空题
1.;2. ;3.;4.;5.;6.;
7.0;8.;9.; 10.;
11.-1; 12.或; 13.92;14.6
二.解答题(计90分)
15.(本小题满分14分)
解:(1) ………… 2分
………… 4分
………… 6分
(2)因为,所以 ………… 7分
1.若,则,∴ …………9分
2. 若,则 ………… 12分
综上 ………… 14分
16.(本小题满分14分)
解:(1) ………… 6分
(2)设=则
…………8分
由题意或 ………… 10分
∴或 …………14分
17.(本小题满分14分)
解:(1)由题意 …………1分
①若则,定义域为 …………4分
②若,则,不等式化为,定义域为 …………7分
(2) ∵
由题意 …………14分
18.(本小题满分16分)
(1)函数f(x))的增区间为,; …………4分
(2) …………8分
(3) …………16分
19.(本题16分)
解:(1)由题意可得:,
则 ………………4分
…………9分
(2)………12分
…………………………………14分
当且仅当,即 时取等号, 取得最大值.此时
所以当,时,取得最大值.……………………………………16分
20.(本小题满分16分)
解:(1)显然f(x)在区间(0,1]上为增函数
∵
∴在区间(0,1]上为减函数,∴f(x)在区间(0,1]上为弱增函数
…………5分
(2)
∵,∴
∴ …………10分
(3)∵当x∈[0,1]时,不等式1-ax≤≤1-bx恒成立
当x=0时,不等式显然成立
当时,但等价于
由(1)为减函数,
∴ …………16分
高二文数学试题
时 间:120分钟 满 分:160分
一.填空题(每题5分,计70分)
1.已知全集,集合,,则 .
2.设,则 (用含的代数式表示)
3.已知复数满足,为虚数单位,则的值为 .
4.函数f(x)=2-3(a>0且a≠1)的图象经过的定点坐标是________.
5.函数在区间上是增函数,那么a的取值范围是 。
6.若,,,则a、b、c从小到大的顺序是 。
7.幂函数在上单调递增,则
8.设函数 若, 则a的取值范围是
9.f(x)是R上的奇函数,当x≥0时,f(x)=x3+ln(1+x),则当x<0时,f(x)= .
10.从,,,,…,推广到第个等式为_________________________.
11.已知是定义在R上的偶函数,并且,当时, 则
12.已知函数的值域为且在上是增函数,则的取值范围是 。
13.十六进制与十进制的对应如下表:
十六进制 1 2 3 4 5 6 7 8 9 10 A B C D E F
十进制 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
例如:A+B=11+12=16+7=F+7=17,所以A+B的值用十六进制表示就等于17。
试计算:A×B+D = (用十六进制表示)
14.已知,
且,则满足条件的所有整数的和是
二.解答题(计90分)
15.(本小题满分14分)已知函数的定义域为集合,函数
的值域为集合.
(1)求;
(2)若集合,且,求实数的取值范围.
16.(本小题满分14分)(1)已知,求实数的值;
(2)已知,若是纯虚数,求.
17.(本小题满分14分)已知函数 (a为常数).
(1)若常数a<2且a≠0,求f(x)的定义域;
(2)若f(x)在区间(2,4)上是减函数,求a的取值范围.
18.(本小题满分16分)已知函数f(x ( http: / / www.21cnjy.com ))是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
(1)写出函数f(x) (x∈R)的增区间;
(2)写出函数f(x) (x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
19.(本小题满分16分)某人准备购置一块 ( http: / / www.21cnjy.com )占地1800平方米的矩形地块(如图),长、宽分别是x米、y米,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路,大棚所占地面积为S平方米,其中a∶b=1∶2.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?
20.(本小题满分16分)在区间D上,如果函数f(x)为增函数,而函数为减函数,则称函数f(x)为“弱增”函数.已知函数f(x)=1-
(1)判断函数f(x)在区间(0,1]上是否为“弱增”函数;
(2)设,,证明:;
(3)当x∈[0,1]时,不等式1-ax≤≤1-bx恒成立,求实数a,b的取值范围.
2015—2016学年度第二学期期期中考试
高二文数学试题答案
一.填空题
1.;2. ;3.;4.;5.;6.;
7.0;8.;9.; 10.;
11.-1; 12.或; 13.92;14.6
二.解答题(计90分)
15.(本小题满分14分)
解:(1) ………… 2分
………… 4分
………… 6分
(2)因为,所以 ………… 7分
1.若,则,∴ …………9分
2. 若,则 ………… 12分
综上 ………… 14分
16.(本小题满分14分)
解:(1) ………… 6分
(2)设=则
…………8分
由题意或 ………… 10分
∴或 …………14分
17.(本小题满分14分)
解:(1)由题意 …………1分
①若则,定义域为 …………4分
②若,则,不等式化为,定义域为 …………7分
(2) ∵
由题意 …………14分
18.(本小题满分16分)
(1)函数f(x))的增区间为,; …………4分
(2) …………8分
(3) …………16分
19.(本题16分)
解:(1)由题意可得:,
则 ………………4分
…………9分
(2)………12分
…………………………………14分
当且仅当,即 时取等号, 取得最大值.此时
所以当,时,取得最大值.……………………………………16分
20.(本小题满分16分)
解:(1)显然f(x)在区间(0,1]上为增函数
∵
∴在区间(0,1]上为减函数,∴f(x)在区间(0,1]上为弱增函数
…………5分
(2)
∵,∴
∴ …………10分
(3)∵当x∈[0,1]时,不等式1-ax≤≤1-bx恒成立
当x=0时,不等式显然成立
当时,但等价于
由(1)为减函数,
∴ …………16分
同课章节目录
