1.1 周期变化 学案(含答案) 2024-2025学年高一数学北师大版(2019)必修第二册
文档属性
| 名称 | 1.1 周期变化 学案(含答案) 2024-2025学年高一数学北师大版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 172.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 20:55:07 | ||
图片预览



文档简介
11 周期变化
【学习目标】
1.了解周期变化在现实中广泛存在.(直观想象)
2.感受周期变化对实际工作的意义.(数学抽象)
3.理解周期变化的概念.(数学抽象)
4.能熟练地判断简单的实际问题的周期.(逻辑推理)
【自主预习】
钟表上的时针每经过12小时转动一周,分针每经过1小时转动一周,秒针每经过1分钟转动一周.假设现在是上午8:00.
1.24小时后的时间是多少 48小时呢
2.时针转动几周,时间是明天上午8:00
3.每天的上午8:00,相隔多长时间 这样的现象,具有怎样的特征
1.(改编)下列现象是周期现象的是( ).
A.台风 B.潮汐
C.海啸 D.地震
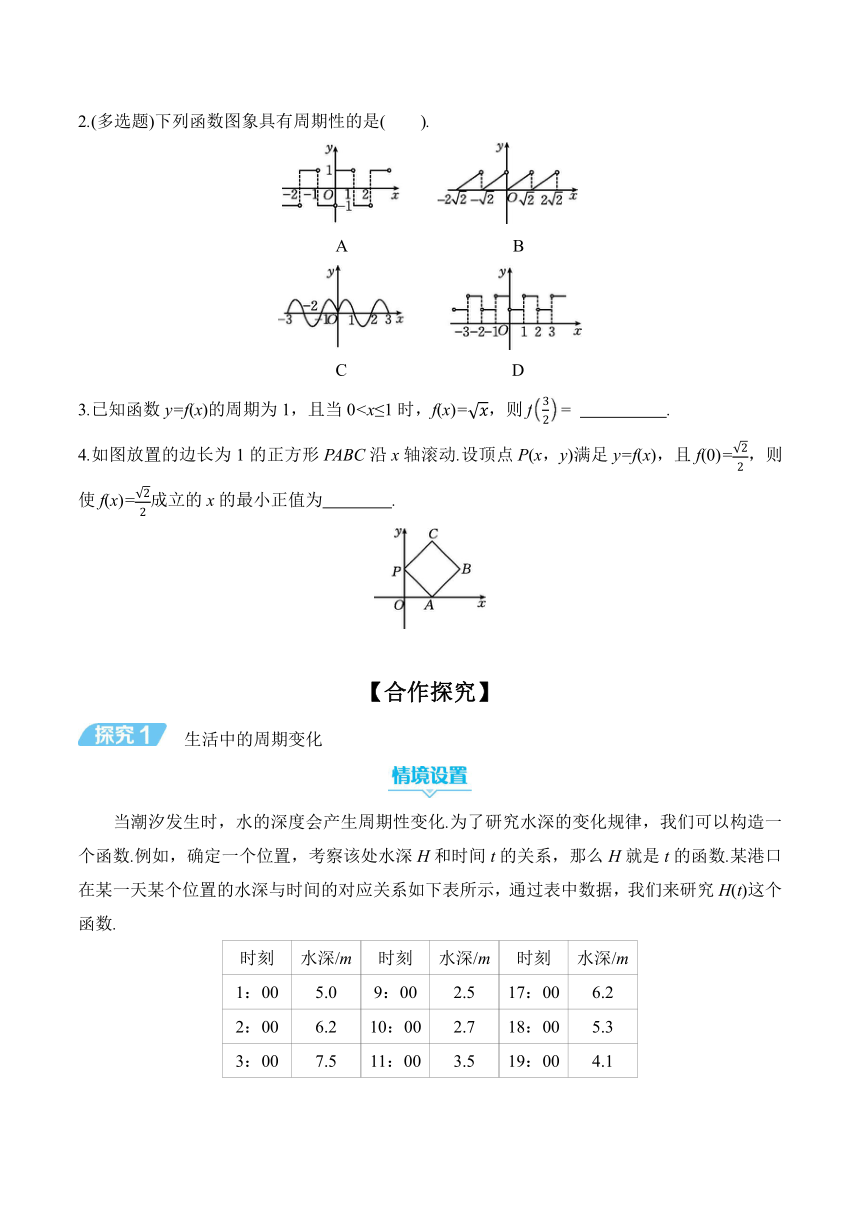
2.(多选题)下列函数图象具有周期性的是( ).
A B
C D
3.已知函数y=f(x)的周期为1,且当04.如图放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)满足y=f(x),且f(0)=,则使f(x)=成立的x的最小正值为 .
【合作探究】
生活中的周期变化
当潮汐发生时,水的深度会产生周期性变化.为了研究水深的变化规律,我们可以构造一个函数.例如,确定一个位置,考察该处水深H和时间t的关系,那么H就是t的函数.某港口在某一天某个位置的水深与时间的对应关系如下表所示,通过表中数据,我们来研究H(t)这个函数.
时刻 水深/m 时刻 水深/m 时刻 水深/m
1:00 5.0 9:00 2.5 17:00 6.2
2:00 6.2 10:00 2.7 18:00 5.3
3:00 7.5 11:00 3.5 19:00 4.1
4:00 7.3 12:00 4.4 20:00 3.1
5:00 6.2 13:00 5.0 21:00 2.5
6:00 5.3 14:00 6.2 22:00 2.7
7:00 4.1 15:00 7.5 23:00 3.5
8:00 3.1 16:00 7.3 24:00 4.4
根据上表提供的数据在坐标纸上可以作出水深H与时间t关系的散点图如下:
问题1:上述变化是周期变化吗
问题2:你能否举出生活中的几个周期变化
问题3:判断周期变化能不能只判定该变化是否重复出现
周期变化
(1)以相同间隔 的变化叫作周期变化.
(2)要判断一种变化是否为周期变化,关键是看每隔一段时间,这种变化是否会 出现.若出现,则为周期变化;否则,不是周期变化.
(1)下列变化中不是周期变化的是( ).
A.“春去春又回”
B.钟表的分针每小时转一圈
C.天干地支表示年、月、日的时间顺序
D.某交通路口每次绿灯通过的车辆数
(2)地球围绕着太阳转(如图),地球到太阳的距离y随时间的变化是周期性的吗
【方法总结】准确理解周期变化的定义是判断是否为周期变化的关键.
如图,这是某人的部分心电图,根据这个心电图,请你判断其心脏跳动是否正常.
周期变化在函数中的应用
将函数f(x)=x2,x∈[-1,1]的图象分别向左、向右平移2,4,6,…个单位长度,观察图象.
问题1:f(-6),f(-4),f(-2),f(0),f(2),f(4),f(6)的值是否相等 f(-7),f(-5),f(-3),f(-1),f(1),f(3),f(5)的值是否相等 由此可以得到f(x+2)与f(x)有什么关系
问题2:利用你所得出的结论,求f,f-,f的值.
对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D,都有x+T∈D且满足f(x+T)=f(x),那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
已知函数f(x)对任意x∈R,都有f(x+2)·f(x)=k(k为常数),当x∈[0,2]时,f(x)=x2+1,则f(5)=( ).
A.1 B.2 C.3 D.5
【方法总结】常见周期函数的形式:周期函数除常见的定义式f(x+T)=f(x)外,还有如下四种形式:(1)f(x+a)=-f(x);(2)f(x+a)=;(3)f(x-a)=-;(4)f(x-a)=f(x+a).以上四种形式的函数都是以|2a|(a≠0)为周期的周期函数.
定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为( ).
A.(-∞,-3) B.(3,+∞)
C.(-∞,-1) D.(1,+∞)
应用周期变化解决实际问题
已知一个匀速运动的水车上装有16个盛水槽,每个盛水槽最多盛水10升,水车5分钟转一圈.
(1)1小时水车转几圈
(2)1小时内最多盛水多少升
【方法总结】 根据函数的周期变化,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.利用周期函数的定义,由函数局部的性质得到函数的整体性质,可以求值、解不等式等,体现了数学抽象的素养.
分针转一圈是1小时,假如现在正好是13点整,那么10圈后是几点 20圈后
呢 (一天24小时制)
【随堂检测】
1.下列变化不是周期变化的是( ).
A.钟摆摆心偏离铅垂线角度的变化
B.游乐场中摩天轮的运行
C.抛一枚骰子,向上的数字是奇数
D.太阳的东升西落
2.函数f(x)是定义在R上的周期为4的奇函数,当0A.2 B.1
C.-1 D.0
3.钟表分针的运动是一个周期变化,其周期为60分钟,现在分针恰好指在2点处,则100分钟后分针指在( ).
A.8点处 B.10点处
C.11点处 D.12点处
4.有这样一个故事:一次毕达哥拉斯处罚学生,要他来回数戴安娜神庙的七根柱子(分别标记为A,B,C,D,E,F,G),一直到指出第2 025个数的柱子的标号是哪一个,才能够停止.你能帮助这名学生尽快结束处罚吗
A B C D E F G
1 2 3 4 5 6 7
12 11 10 9 8
13 14 15 16 17 18 19
24 23 22 21 20
25 …
参考答案
1.1 周期变化
自主预习·悟新知
预学忆思
1.明天上午8:00;后天上午8:00.
2.2周.
3.24小时的整数倍.周而复始,重复出现.
自学检测
1.B 【解析】潮汐是海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动;而台风、海啸和地震是随机现象.故选B.
2.ABD 【解析】抓住周期变化的重复性特点,可知A,B,D对应的函数为周期函数.
对于C,图象不重复出现,故不符合题意.故选ABD.
3. 【解析】由题意知,函数f(x) 的周期为1,所以f=f+1=f==.
4.2+ 【解析】设正方形PABC沿x轴正方向滚动.沿x轴的正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.点P的部分运动轨迹如图所示.
根据图象知,满足f(x)=的x的最小正值是2+.
合作探究·提素养
探究1 情境设置
问题1:从列表和散点图可以看出,每经过相同的时间间隔t(12 h),水深就重复出现相同的数值,因此,水深是周期性变化的.
问题2:钟摆的摆动、地球公转、交通路口的红绿灯变化、城市里霓虹灯的闪烁变幻等.
问题3:不可以,因为周期变化必须是间隔相同的时间重复出现.
新知生成
(1)重复出现 (2)重复
新知运用
例1 (1)D 【解析】(1)由周期变化的概念易知,某交通路口每次绿灯通过的车辆数不是周期变化.故选D.
(2)根据物理学知识,我们知道在任何一个确定的时刻,地球与太阳的距离y是唯一确定的,每经过一年地球围绕着太阳旋转一周.无论从哪个时刻t算起,经过一年时间,地球又会回到原来的位置,所以,地球与太阳的距离是周期变化的.
巩固训练 【解析】观察图象可知,此人的心电图是周期性变化的,因此心脏跳动正常.
探究2 情境设置
问题1:f(-6)=f(-4)=f(-2)=f(0)=f(2)=f(4)=f(6)=0.
f(-7)=f(-5)=f(-3)=f(-1)=f(1)=f(3)=f(5)=1.
由以上结论可得f(x+2)=f(x).
问题2:f=f=…=f-=,f-=f=,f=f-=.
新知运用
例2 B 【解析】因为f(0)=1,f(2)=5,所以f(0+2)·f(0)=5=k,
所以f(x+2)·f(x)=5,所以f(x+4)·f(x+2)=5,故f(x+4)=f(x),
所以函数的周期为4,故f(5)=f(1)=12+1=2,故选B.
巩固训练 D 【解析】因为f(x+3)=f(x),所以f(x)是定义在R上的以3为周期的函数,所以f(7)=f(7-9)=f(-2).
又因为函数f(x)是偶函数,
所以f(-2)=f(2),所以f(7)=f(2)>1,
所以a>1,即a∈(1,+∞).故选D.
探究3
例3 【解析】(1)因为1小时=60分钟=12×5分钟,且水车5分钟转一圈,所以1小时水车转12圈.
(2)因为水车上装有16个盛水槽,每个盛水槽最多盛水10升,所以每转一圈,最多盛水16×10=160(升),所以水车1小时内最多盛水160×12=1 920(升).
巩固训练 【解析】10圈后是13+10=23点,20圈后是13+20-24=9点,为第二天上午9点整.
随堂检测·精评价
1.C 【解析】A,B,D所述都是周期变化,而C中“向上的数字是奇数”不是周期变化.
2.C 【解析】∵函数f(x)是定义在R上的周期为4的奇函数,
∴f(-9)=f(-9+2×4)=f(-1)=-f(1)=-1.故选C.
3.B 【解析】由题意知,60分钟后分针仍指在2点处,100分钟后指在2+=10点处.
4.【解析】能.
易知从A开始数,周期为12,而2 025=12×168+9,
所以标号为E的柱子就是数到第2 025个数的那根柱子.
【学习目标】
1.了解周期变化在现实中广泛存在.(直观想象)
2.感受周期变化对实际工作的意义.(数学抽象)
3.理解周期变化的概念.(数学抽象)
4.能熟练地判断简单的实际问题的周期.(逻辑推理)
【自主预习】
钟表上的时针每经过12小时转动一周,分针每经过1小时转动一周,秒针每经过1分钟转动一周.假设现在是上午8:00.
1.24小时后的时间是多少 48小时呢
2.时针转动几周,时间是明天上午8:00
3.每天的上午8:00,相隔多长时间 这样的现象,具有怎样的特征
1.(改编)下列现象是周期现象的是( ).
A.台风 B.潮汐
C.海啸 D.地震
2.(多选题)下列函数图象具有周期性的是( ).
A B
C D
3.已知函数y=f(x)的周期为1,且当0
【合作探究】
生活中的周期变化
当潮汐发生时,水的深度会产生周期性变化.为了研究水深的变化规律,我们可以构造一个函数.例如,确定一个位置,考察该处水深H和时间t的关系,那么H就是t的函数.某港口在某一天某个位置的水深与时间的对应关系如下表所示,通过表中数据,我们来研究H(t)这个函数.
时刻 水深/m 时刻 水深/m 时刻 水深/m
1:00 5.0 9:00 2.5 17:00 6.2
2:00 6.2 10:00 2.7 18:00 5.3
3:00 7.5 11:00 3.5 19:00 4.1
4:00 7.3 12:00 4.4 20:00 3.1
5:00 6.2 13:00 5.0 21:00 2.5
6:00 5.3 14:00 6.2 22:00 2.7
7:00 4.1 15:00 7.5 23:00 3.5
8:00 3.1 16:00 7.3 24:00 4.4
根据上表提供的数据在坐标纸上可以作出水深H与时间t关系的散点图如下:
问题1:上述变化是周期变化吗
问题2:你能否举出生活中的几个周期变化
问题3:判断周期变化能不能只判定该变化是否重复出现
周期变化
(1)以相同间隔 的变化叫作周期变化.
(2)要判断一种变化是否为周期变化,关键是看每隔一段时间,这种变化是否会 出现.若出现,则为周期变化;否则,不是周期变化.
(1)下列变化中不是周期变化的是( ).
A.“春去春又回”
B.钟表的分针每小时转一圈
C.天干地支表示年、月、日的时间顺序
D.某交通路口每次绿灯通过的车辆数
(2)地球围绕着太阳转(如图),地球到太阳的距离y随时间的变化是周期性的吗
【方法总结】准确理解周期变化的定义是判断是否为周期变化的关键.
如图,这是某人的部分心电图,根据这个心电图,请你判断其心脏跳动是否正常.
周期变化在函数中的应用
将函数f(x)=x2,x∈[-1,1]的图象分别向左、向右平移2,4,6,…个单位长度,观察图象.
问题1:f(-6),f(-4),f(-2),f(0),f(2),f(4),f(6)的值是否相等 f(-7),f(-5),f(-3),f(-1),f(1),f(3),f(5)的值是否相等 由此可以得到f(x+2)与f(x)有什么关系
问题2:利用你所得出的结论,求f,f-,f的值.
对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D,都有x+T∈D且满足f(x+T)=f(x),那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
已知函数f(x)对任意x∈R,都有f(x+2)·f(x)=k(k为常数),当x∈[0,2]时,f(x)=x2+1,则f(5)=( ).
A.1 B.2 C.3 D.5
【方法总结】常见周期函数的形式:周期函数除常见的定义式f(x+T)=f(x)外,还有如下四种形式:(1)f(x+a)=-f(x);(2)f(x+a)=;(3)f(x-a)=-;(4)f(x-a)=f(x+a).以上四种形式的函数都是以|2a|(a≠0)为周期的周期函数.
定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为( ).
A.(-∞,-3) B.(3,+∞)
C.(-∞,-1) D.(1,+∞)
应用周期变化解决实际问题
已知一个匀速运动的水车上装有16个盛水槽,每个盛水槽最多盛水10升,水车5分钟转一圈.
(1)1小时水车转几圈
(2)1小时内最多盛水多少升
【方法总结】 根据函数的周期变化,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.利用周期函数的定义,由函数局部的性质得到函数的整体性质,可以求值、解不等式等,体现了数学抽象的素养.
分针转一圈是1小时,假如现在正好是13点整,那么10圈后是几点 20圈后
呢 (一天24小时制)
【随堂检测】
1.下列变化不是周期变化的是( ).
A.钟摆摆心偏离铅垂线角度的变化
B.游乐场中摩天轮的运行
C.抛一枚骰子,向上的数字是奇数
D.太阳的东升西落
2.函数f(x)是定义在R上的周期为4的奇函数,当0
C.-1 D.0
3.钟表分针的运动是一个周期变化,其周期为60分钟,现在分针恰好指在2点处,则100分钟后分针指在( ).
A.8点处 B.10点处
C.11点处 D.12点处
4.有这样一个故事:一次毕达哥拉斯处罚学生,要他来回数戴安娜神庙的七根柱子(分别标记为A,B,C,D,E,F,G),一直到指出第2 025个数的柱子的标号是哪一个,才能够停止.你能帮助这名学生尽快结束处罚吗
A B C D E F G
1 2 3 4 5 6 7
12 11 10 9 8
13 14 15 16 17 18 19
24 23 22 21 20
25 …
参考答案
1.1 周期变化
自主预习·悟新知
预学忆思
1.明天上午8:00;后天上午8:00.
2.2周.
3.24小时的整数倍.周而复始,重复出现.
自学检测
1.B 【解析】潮汐是海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动;而台风、海啸和地震是随机现象.故选B.
2.ABD 【解析】抓住周期变化的重复性特点,可知A,B,D对应的函数为周期函数.
对于C,图象不重复出现,故不符合题意.故选ABD.
3. 【解析】由题意知,函数f(x) 的周期为1,所以f=f+1=f==.
4.2+ 【解析】设正方形PABC沿x轴正方向滚动.沿x轴的正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.点P的部分运动轨迹如图所示.
根据图象知,满足f(x)=的x的最小正值是2+.
合作探究·提素养
探究1 情境设置
问题1:从列表和散点图可以看出,每经过相同的时间间隔t(12 h),水深就重复出现相同的数值,因此,水深是周期性变化的.
问题2:钟摆的摆动、地球公转、交通路口的红绿灯变化、城市里霓虹灯的闪烁变幻等.
问题3:不可以,因为周期变化必须是间隔相同的时间重复出现.
新知生成
(1)重复出现 (2)重复
新知运用
例1 (1)D 【解析】(1)由周期变化的概念易知,某交通路口每次绿灯通过的车辆数不是周期变化.故选D.
(2)根据物理学知识,我们知道在任何一个确定的时刻,地球与太阳的距离y是唯一确定的,每经过一年地球围绕着太阳旋转一周.无论从哪个时刻t算起,经过一年时间,地球又会回到原来的位置,所以,地球与太阳的距离是周期变化的.
巩固训练 【解析】观察图象可知,此人的心电图是周期性变化的,因此心脏跳动正常.
探究2 情境设置
问题1:f(-6)=f(-4)=f(-2)=f(0)=f(2)=f(4)=f(6)=0.
f(-7)=f(-5)=f(-3)=f(-1)=f(1)=f(3)=f(5)=1.
由以上结论可得f(x+2)=f(x).
问题2:f=f=…=f-=,f-=f=,f=f-=.
新知运用
例2 B 【解析】因为f(0)=1,f(2)=5,所以f(0+2)·f(0)=5=k,
所以f(x+2)·f(x)=5,所以f(x+4)·f(x+2)=5,故f(x+4)=f(x),
所以函数的周期为4,故f(5)=f(1)=12+1=2,故选B.
巩固训练 D 【解析】因为f(x+3)=f(x),所以f(x)是定义在R上的以3为周期的函数,所以f(7)=f(7-9)=f(-2).
又因为函数f(x)是偶函数,
所以f(-2)=f(2),所以f(7)=f(2)>1,
所以a>1,即a∈(1,+∞).故选D.
探究3
例3 【解析】(1)因为1小时=60分钟=12×5分钟,且水车5分钟转一圈,所以1小时水车转12圈.
(2)因为水车上装有16个盛水槽,每个盛水槽最多盛水10升,所以每转一圈,最多盛水16×10=160(升),所以水车1小时内最多盛水160×12=1 920(升).
巩固训练 【解析】10圈后是13+10=23点,20圈后是13+20-24=9点,为第二天上午9点整.
随堂检测·精评价
1.C 【解析】A,B,D所述都是周期变化,而C中“向上的数字是奇数”不是周期变化.
2.C 【解析】∵函数f(x)是定义在R上的周期为4的奇函数,
∴f(-9)=f(-9+2×4)=f(-1)=-f(1)=-1.故选C.
3.B 【解析】由题意知,60分钟后分针仍指在2点处,100分钟后指在2+=10点处.
4.【解析】能.
易知从A开始数,周期为12,而2 025=12×168+9,
所以标号为E的柱子就是数到第2 025个数的那根柱子.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
