2.4.1 平面向量基本定理 学案(含答案)2024-2025学年高一数学北师大版(2019)必修第二册
文档属性
| 名称 | 2.4.1 平面向量基本定理 学案(含答案)2024-2025学年高一数学北师大版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 21:25:03 | ||
图片预览



文档简介
2.4.1 平面向量基本定理
【学习目标】
1.理解基的含义,并能判断两个向量是否构成一组基.(逻辑推理)
2.理解平面向量基本定理及其意义.(数学抽象)
3.会用基表示平面向量.(逻辑推理)
【自主预习】
音乐是人们在休闲时候的一种选择,不管是通俗的流行歌曲、动感的摇滚音乐,还是高雅的古典音乐,它们都给了人们不同的享受、不一样的感觉.事实上,音乐有基本音符Do Re Mi Fa So La Si,所有的乐谱都是这几个音符的巧妙组合,音乐的奇妙就在于此.
阅读教材,回答下列问题.
1.在平面向量中,我们能否找到它的“基本音符”呢 你发现它是什么
2.我们知道两个力可以合成一个力,反之一个力可以分解为两个力.向量a是否也可以分解为两个向量呢
3.0能与另外一个向量a构成一组基吗
1.在△ABC中,=2,E为AD的中点,以,为一组基,则=( ).
A.- B.-
C.- D.2-
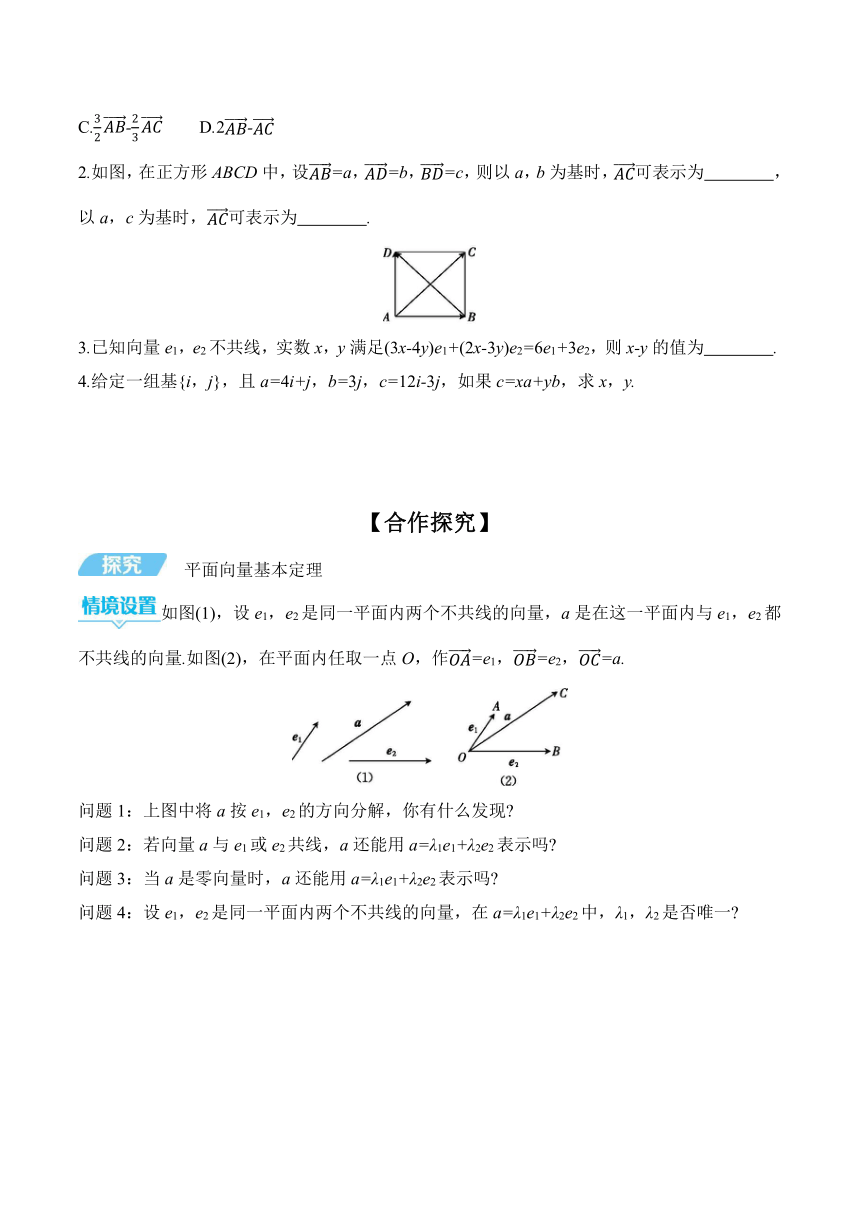
2.如图,在正方形ABCD中,设=a,=b,=c,则以a,b为基时,可表示为 ,以a,c为基时,可表示为 .
3.已知向量e1,e2不共线,实数x,y满足(3x-4y)e1+(2x-3y)e2=6e1+3e2,则x-y的值为 .
4.给定一组基{i,j},且a=4i+j,b=3j,c=12i-3j,如果c=xa+yb,求x,y.
【合作探究】
平面向量基本定理
如图(1),设e1,e2是同一平面内两个不共线的向量,a是在这一平面内与e1,e2都不共线的向量.如图(2),在平面内任取一点O,作=e1,=e2,=a.
问题1:上图中将a按e1,e2的方向分解,你有什么发现
问题2:若向量a与e1或e2共线,a还能用a=λ1e1+λ2e2表示吗
问题3:当a是零向量时,a还能用a=λ1e1+λ2e2表示吗
问题4:设e1,e2是同一平面内两个不共线的向量,在a=λ1e1+λ2e2中,λ1,λ2是否唯一
1.平面向量基本定理:如果e1,e2是同一平面内的两个不共线的向量,那么对于这一平面内的任意一个向量a,存在唯一一对实数λ1,λ2,使得a=λ1e1+λ2e2.
2.基:若e1,e2不共线,把e1,e2叫作表示这一平面内所有向量的一组 .平面内任一向量都可以用同一组基唯一表示.
3.若基中的两个向量互相垂直,则称这组基为正交基.在正交基下向量的线性表示称为正交分解.
若基中的两个向量是互相垂直的单位向量,则称这组基为标准正交基.
一、对基的理解
如果e1,e2是平面α内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基的是( ).
A.e1与e1+e2 B.e1-2e2与e1+2e2
C.e1+e2与e1-e2 D.e1+3e2与2e1+6e2
【方法总结】对基的理解:两个向量能否作为一组基,关键是看这两个向量是否共线.若共线,则不能作基;反之,则可作基.
二、用基表示向量
如图所示,在△ABC中,M是AB的中点,且=,BN与CM相交于点E,设=a,=b,试用基{a,b}表示向量.
【方法总结】将两个不共线的向量作为基表示其他向量,基本方法有两种:一种是运用向量的线性运算法则对所求向量不断进行转化,直至能用基表示为止;另一种是通过列向量方程或方程组的形式,利用基表示向量的唯一性求解.
三、平面向量基本定理的应用
如图所示,L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0,求证:l=m=n.
【方法总结】平面向量基本定理是向量法的理论基础,它不仅提供了向量的几何表示方法,而且使向量用坐标来表示成为可能,从而架起了向量的几何运算与代数运算之间的桥梁,这就为几何问题转化为代数论证提供了理论工具.
若向量a,b不共线,则c=2a-b,d=3a-2b,试判断c,d能否作为一组基.
如图所示,在 ABCD中,E,F分别为BC,DC边上的中点,若=a,=b,试用a,b表示向量,.
【随堂检测】
1.已知平行四边形ABCD,则下列各组向量是该平面内所有向量的基的是( ).
A., B.,
C., D.,
2.在△ABC中,D是BC边的中点,E是AD的中点,若=λ+μ,则λ+μ的值是( ).
A.1 B. C.- D.-
3.如图,C,D是△AOB的边AB的三等分点,设=e1,=e2,以e1,e2为一组基,则= ,= .
4.在△ABC中,F是边AB上靠近点B的四等分点,试以=e1,=e2为一组基表示.
参考答案
课时1 平面向量基本定理
自主预习·悟新知
预学忆思
1.能,它是基.
2.因为力是向量,所以向量a也可以分解为两个向量.
3. 不能.基向量是不共线的,而0与任意向量共线.
自学检测
1.A 【解析】=-+=-×=-+=-.
2.a+b 2a+c 【解析】以a,b为基时,=a+b;以a,c为基时,=+=a+c,=+=+=a+a+c=2a+c.
3.3 【解析】∵e1,e2不共线,∴由平面向量基本定理可得故x-y=3.
4.【解析】因为c=xa+yb=x(4i+j)+y(3j)=4xi+(x+3y)j,c=12i-3j,
所以解得
合作探究·提素养
探究 情境设置
问题1:如图,a==+=λ1e1+λ2e2.
问题2:能,当向量a与e1共线时,a=λ1e1+0e2;
当向量a与e2共线时,a=0e1+λ2e2.
问题3:能,a=0e1+0e2.
问题4:假设a=μ1e1+μ2e2,则λ1e1+λ2e2=μ1e1+μ2e2,即(λ1-μ1)e1+(λ2-μ2)e2=0,所以λ1-μ1=0且λ2-μ2=0,即λ1=μ1且λ2=μ2,所以λ1,λ2唯一.
新知生成
2.基
新知运用
例1 D 【解析】对于A,设e1+e2=λe1,则所以λ无解;
对于B,设e1-2e2=λ(e1+2e2),则所以λ无解;
对于C,设e1+e2=λ(e1-e2),则所以λ无解;
对于D,设e1+3e2=λ(2e1+6e2),则解得λ=,所以这两个向量是共线向量.
故D中向量不能作为平面内所有向量的一组基,故选D.
例2 【解析】易得==b,==a,
由N,E,B三点共线知,存在实数m,
满足=m+(1-m)=mb+(1-m)a.
由C,E,M三点共线知,存在实数n,
满足=n+(1-n)=na+(1-n)b,
所以mb+(1-m)a=na+(1-n)b.
因为{a,b}为基,所以解得
所以=a+b.
例3 【解析】令=a,=b为一组基,
根据已知有=la,=mb.
∵=+=-a-b,∴=n=-na-nb,
∴=+=(l-1)a-b,=+=a+mb,=+=-na+(1-n)b.
又++=0,
∴(l-n)a+(m-n)b=0.
根据平面向量基本定理,有l-n=m-n=0,故l=m=n.
巩固训练1 【解析】设存在实数λ,使得c=λd,
则2a-b=λ(3a-2b),即(2-3λ)a+(2λ-1)b=0,
因为向量a,b不共线,所以2-3λ=2λ-1=0,这样的λ是不存在的,
所以c,d不共线,故c,d能作为一组基.
巩固训练2 【解析】=++
=-++
=-++=a-b.
=++
=-++=b-a.
随堂检测·精评价
1.D 【解析】因为,不共线,所以是一组基.
2.D 【解析】由D是BC边的中点,E是AD的中点,得=(+),==(+),所以=+=-+(+)=-,所以λ=,μ=-,故λ+μ=-.
3.e1+e2 e1+e2 【解析】=+=+=e1+(e2-e1)=e1+e2,
=+=+
=e1+e2+(e2-e1)=e1+e2.
4.【解析】∵=-=e1-e2,且F是边AB上靠近点B的四等分点,
∴==(e1-e2),
∴=+=e2+(e1-e2)=e1+e2.
【学习目标】
1.理解基的含义,并能判断两个向量是否构成一组基.(逻辑推理)
2.理解平面向量基本定理及其意义.(数学抽象)
3.会用基表示平面向量.(逻辑推理)
【自主预习】
音乐是人们在休闲时候的一种选择,不管是通俗的流行歌曲、动感的摇滚音乐,还是高雅的古典音乐,它们都给了人们不同的享受、不一样的感觉.事实上,音乐有基本音符Do Re Mi Fa So La Si,所有的乐谱都是这几个音符的巧妙组合,音乐的奇妙就在于此.
阅读教材,回答下列问题.
1.在平面向量中,我们能否找到它的“基本音符”呢 你发现它是什么
2.我们知道两个力可以合成一个力,反之一个力可以分解为两个力.向量a是否也可以分解为两个向量呢
3.0能与另外一个向量a构成一组基吗
1.在△ABC中,=2,E为AD的中点,以,为一组基,则=( ).
A.- B.-
C.- D.2-
2.如图,在正方形ABCD中,设=a,=b,=c,则以a,b为基时,可表示为 ,以a,c为基时,可表示为 .
3.已知向量e1,e2不共线,实数x,y满足(3x-4y)e1+(2x-3y)e2=6e1+3e2,则x-y的值为 .
4.给定一组基{i,j},且a=4i+j,b=3j,c=12i-3j,如果c=xa+yb,求x,y.
【合作探究】
平面向量基本定理
如图(1),设e1,e2是同一平面内两个不共线的向量,a是在这一平面内与e1,e2都不共线的向量.如图(2),在平面内任取一点O,作=e1,=e2,=a.
问题1:上图中将a按e1,e2的方向分解,你有什么发现
问题2:若向量a与e1或e2共线,a还能用a=λ1e1+λ2e2表示吗
问题3:当a是零向量时,a还能用a=λ1e1+λ2e2表示吗
问题4:设e1,e2是同一平面内两个不共线的向量,在a=λ1e1+λ2e2中,λ1,λ2是否唯一
1.平面向量基本定理:如果e1,e2是同一平面内的两个不共线的向量,那么对于这一平面内的任意一个向量a,存在唯一一对实数λ1,λ2,使得a=λ1e1+λ2e2.
2.基:若e1,e2不共线,把e1,e2叫作表示这一平面内所有向量的一组 .平面内任一向量都可以用同一组基唯一表示.
3.若基中的两个向量互相垂直,则称这组基为正交基.在正交基下向量的线性表示称为正交分解.
若基中的两个向量是互相垂直的单位向量,则称这组基为标准正交基.
一、对基的理解
如果e1,e2是平面α内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基的是( ).
A.e1与e1+e2 B.e1-2e2与e1+2e2
C.e1+e2与e1-e2 D.e1+3e2与2e1+6e2
【方法总结】对基的理解:两个向量能否作为一组基,关键是看这两个向量是否共线.若共线,则不能作基;反之,则可作基.
二、用基表示向量
如图所示,在△ABC中,M是AB的中点,且=,BN与CM相交于点E,设=a,=b,试用基{a,b}表示向量.
【方法总结】将两个不共线的向量作为基表示其他向量,基本方法有两种:一种是运用向量的线性运算法则对所求向量不断进行转化,直至能用基表示为止;另一种是通过列向量方程或方程组的形式,利用基表示向量的唯一性求解.
三、平面向量基本定理的应用
如图所示,L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0,求证:l=m=n.
【方法总结】平面向量基本定理是向量法的理论基础,它不仅提供了向量的几何表示方法,而且使向量用坐标来表示成为可能,从而架起了向量的几何运算与代数运算之间的桥梁,这就为几何问题转化为代数论证提供了理论工具.
若向量a,b不共线,则c=2a-b,d=3a-2b,试判断c,d能否作为一组基.
如图所示,在 ABCD中,E,F分别为BC,DC边上的中点,若=a,=b,试用a,b表示向量,.
【随堂检测】
1.已知平行四边形ABCD,则下列各组向量是该平面内所有向量的基的是( ).
A., B.,
C., D.,
2.在△ABC中,D是BC边的中点,E是AD的中点,若=λ+μ,则λ+μ的值是( ).
A.1 B. C.- D.-
3.如图,C,D是△AOB的边AB的三等分点,设=e1,=e2,以e1,e2为一组基,则= ,= .
4.在△ABC中,F是边AB上靠近点B的四等分点,试以=e1,=e2为一组基表示.
参考答案
课时1 平面向量基本定理
自主预习·悟新知
预学忆思
1.能,它是基.
2.因为力是向量,所以向量a也可以分解为两个向量.
3. 不能.基向量是不共线的,而0与任意向量共线.
自学检测
1.A 【解析】=-+=-×=-+=-.
2.a+b 2a+c 【解析】以a,b为基时,=a+b;以a,c为基时,=+=a+c,=+=+=a+a+c=2a+c.
3.3 【解析】∵e1,e2不共线,∴由平面向量基本定理可得故x-y=3.
4.【解析】因为c=xa+yb=x(4i+j)+y(3j)=4xi+(x+3y)j,c=12i-3j,
所以解得
合作探究·提素养
探究 情境设置
问题1:如图,a==+=λ1e1+λ2e2.
问题2:能,当向量a与e1共线时,a=λ1e1+0e2;
当向量a与e2共线时,a=0e1+λ2e2.
问题3:能,a=0e1+0e2.
问题4:假设a=μ1e1+μ2e2,则λ1e1+λ2e2=μ1e1+μ2e2,即(λ1-μ1)e1+(λ2-μ2)e2=0,所以λ1-μ1=0且λ2-μ2=0,即λ1=μ1且λ2=μ2,所以λ1,λ2唯一.
新知生成
2.基
新知运用
例1 D 【解析】对于A,设e1+e2=λe1,则所以λ无解;
对于B,设e1-2e2=λ(e1+2e2),则所以λ无解;
对于C,设e1+e2=λ(e1-e2),则所以λ无解;
对于D,设e1+3e2=λ(2e1+6e2),则解得λ=,所以这两个向量是共线向量.
故D中向量不能作为平面内所有向量的一组基,故选D.
例2 【解析】易得==b,==a,
由N,E,B三点共线知,存在实数m,
满足=m+(1-m)=mb+(1-m)a.
由C,E,M三点共线知,存在实数n,
满足=n+(1-n)=na+(1-n)b,
所以mb+(1-m)a=na+(1-n)b.
因为{a,b}为基,所以解得
所以=a+b.
例3 【解析】令=a,=b为一组基,
根据已知有=la,=mb.
∵=+=-a-b,∴=n=-na-nb,
∴=+=(l-1)a-b,=+=a+mb,=+=-na+(1-n)b.
又++=0,
∴(l-n)a+(m-n)b=0.
根据平面向量基本定理,有l-n=m-n=0,故l=m=n.
巩固训练1 【解析】设存在实数λ,使得c=λd,
则2a-b=λ(3a-2b),即(2-3λ)a+(2λ-1)b=0,
因为向量a,b不共线,所以2-3λ=2λ-1=0,这样的λ是不存在的,
所以c,d不共线,故c,d能作为一组基.
巩固训练2 【解析】=++
=-++
=-++=a-b.
=++
=-++=b-a.
随堂检测·精评价
1.D 【解析】因为,不共线,所以是一组基.
2.D 【解析】由D是BC边的中点,E是AD的中点,得=(+),==(+),所以=+=-+(+)=-,所以λ=,μ=-,故λ+μ=-.
3.e1+e2 e1+e2 【解析】=+=+=e1+(e2-e1)=e1+e2,
=+=+
=e1+e2+(e2-e1)=e1+e2.
4.【解析】∵=-=e1-e2,且F是边AB上靠近点B的四等分点,
∴==(e1-e2),
∴=+=e2+(e1-e2)=e1+e2.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
