2.6.4 余弦定理、正弦定理应用举例 同步学案(含答案) 2024-2025学年高一数学北师大版(2019)必修第二册
文档属性
| 名称 | 2.6.4 余弦定理、正弦定理应用举例 同步学案(含答案) 2024-2025学年高一数学北师大版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 278.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览




文档简介
2.6.4 余弦定理、正弦定理应用举例
【学习目标】
1.熟练掌握正、余弦定理.(数学抽象)
2.能够运用正、余弦定理等知识和方法求解距离、高度、角度问题.(数学抽象)
【自主预习】
1.在浩瀚无垠的海面上航行,最重要的是定位和保持航向.阅读教材,看看船只是如何表达位置和航向的
2.方位角和方向角是如何定义的
3.在△ABC中,角A,B,C的对边分别为a,b,c,试写出用两边及夹角表示的三角形面积公式.
4.如何不登月测量地月的大致距离
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)仰角是视线与视线在水平面的射影的夹角. ( )
(2)两点间不可通又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解. ( )
(3)两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解. ( )
(4)高度问题大多通过正(余)弦定理构造直角三角形来解决. ( )
2.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为( ).
A.50 m B.50 m C.25 m D. m
3.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为( ).
A.20 m
B.30 m
C.20 m
D.30 m
4.一船以15 km/h的速度向东行驶,船在A处看到一灯塔B在北偏东60°的方向上,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°的方向上,这时船与灯塔的距离为 km.
【合作探究】
测量距离问题
问题1:如图所示,A,B两点在河的两岸,在点A的一侧,需测出哪些量,可以求出A,B两点的距离
问题2:如图所示,A,B两点都在河的对岸(不可到达),结合图形,需测出哪些量,可以求出A,B两点间的距离
1.基线的概念与选择原则
(1)定义:在测量上,根据测量需要适当确定的 叫作基线.
(2)性质:在测量过程中,要根据实际需要选取合适的 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越 .
2.测量不可到达的两点间的距离,若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;若两点均不可到达,则需用3个三角形才能解决,一般正、余弦定理都要用到.
如图,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A,B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=100米,则该河段的宽度为 米.参考数据:sin 75°=
在某次军事演习中,红方为了准确分析战场形势,在两个相距为a的军事基地C和D测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则蓝方这两支精锐部队的距离是 .参考数据:sin 75°=
【方法总结】三角形中与距离有关的问题的求解策略:
(1)解决三角形中与距离有关的问题时,若在一个三角形中,则直接利用正弦定理、余弦定理求解即可;若所求的线段在多个三角形中,则要根据条件选择适当的三角形,再利用正弦定理、余弦定理求解.
(2)解决三角形中与距离有关的问题的关键是转化为求三角形中的边,分析所解三角形中已知哪些元素,还需要求出哪些元素,灵活应用正弦定理、余弦定理来解决.
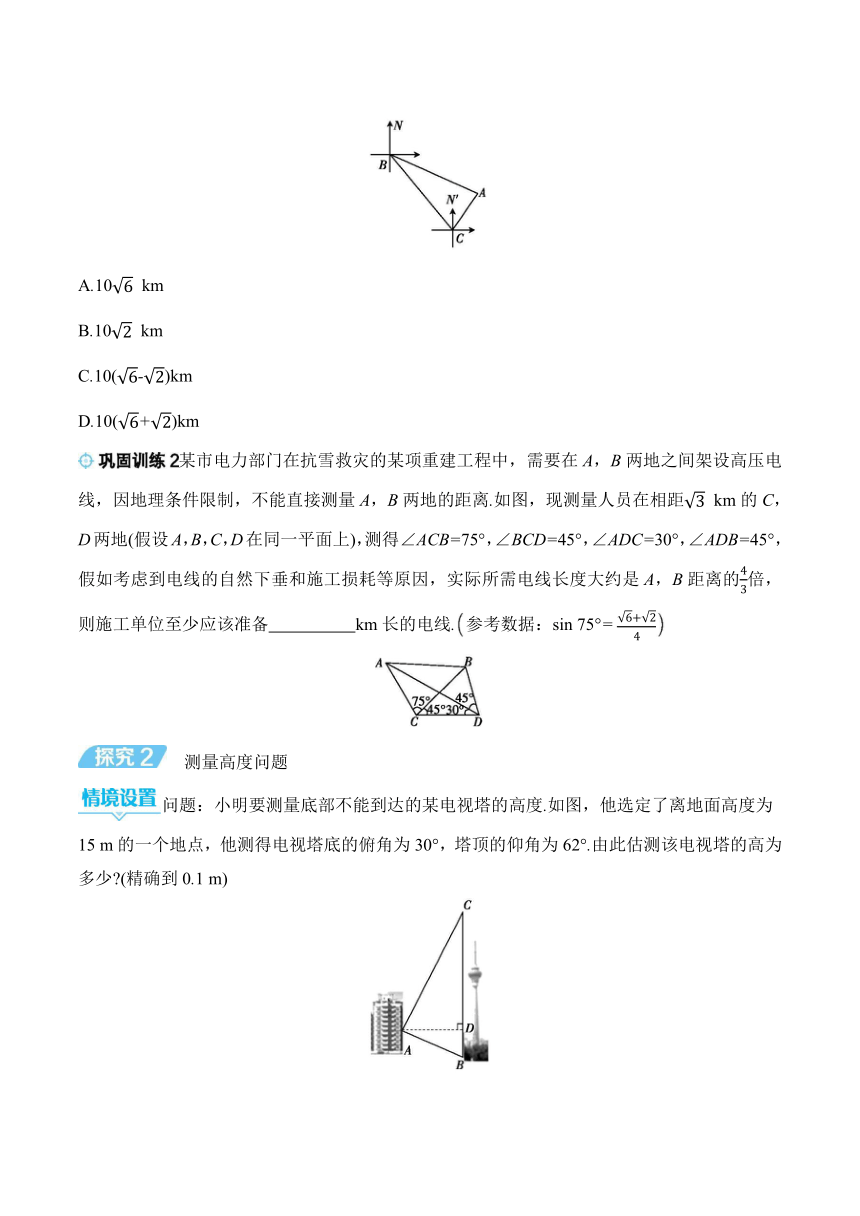
如图,货轮在海上以40 km/h的速度由B向C航行,航行的方位角∠NBC=140°,A处有灯塔,方位角∠NBA=110°.在C处观察灯塔A的方位角∠N'CA=35°,由B到C需要航行半小时,则C到灯塔A的距离是( ).参考数据:sin 75°=
A.10 km
B.10 km
C.10(-)km
D.10(+)km
某市电力部门在抗雪救灾的某项重建工程中,需要在A,B两地之间架设高压电线,因地理条件限制,不能直接测量A,B两地的距离.如图,现测量人员在相距 km的C,D两地(假设A,B,C,D在同一平面上),测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,假如考虑到电线的自然下垂和施工损耗等原因,实际所需电线长度大约是A,B距离的倍,则施工单位至少应该准备 km长的电线.参考数据:sin 75°=
测量高度问题
问题:小明要测量底部不能到达的某电视塔的高度.如图,他选定了离地面高度为15 m的一个地点,他测得电视塔底的俯角为30°,塔顶的仰角为62°.由此估测该电视塔的高为多少 (精确到0.1 m)
1.仰角和俯角:与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫 ,目标视线在水平视线下方时叫 (如图所示).
视角:从眼睛的中心向物体两端所引的两条直线的 ,如图所示,视角50°指的是观察该物体的两端视线张开的角度.
一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的A处测得水柱顶端的仰角为45°,沿A向北偏东30°方向前进100 m到达B处,在B处测得水柱顶端的仰角为30°,则水柱的高度是( ).
A.50 m B.100 m
C.120 m D.150 m
【方法总结】解题思路
某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1 000 m后到达D处,又测得山顶B的仰角为65°,则山的高度约为 m.(精确到1 m,参考数据:≈1.414,sin 35°≈0.574)
测量角度问题
请结合下图,探究下面的问题.
问题:你能用方向角表述图中的角吗
1.方向角
从指定方向线到 方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°(如图所示).
2.方位角
从正北方向 转到目标方向线所成的水平角.如点B的方位角为α(如图所示).
方位角的取值范围: .
甲船在A点发现乙船在北偏东60°的B处,乙船以a海里/时的速度向北行驶,已知甲船的速度是a海里/时,问甲船应沿什么方向前进才能最快与乙船相遇
【方法总结】运用正弦定理、余弦定理解决实际问题的基本步骤:
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形).
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型.
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解.
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
如图所示,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10海里/时的速度追截走私船,此时走私船正以10海里/时的速度从B处向北偏东30°方向逃窜.问:缉私船应
沿什么方向行驶才能最快截获走私船 并求出所需时间.
【随堂检测】
1.学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为4 m,A=30°,则其跨度AB的长为( ).
A.12 m B.8 m
C.3 m D.4 m
2.身高相同的甲、乙两人在同一地平面上的不同方向观测20 m高的旗杆,甲观测的仰角为50°,乙观测的仰角为40°,用d1,d2分别表示甲、乙两人离旗杆的距离,那么有( ).
A.d1>d2 B.d1C.d1>20 m D.d2<20 m
3.某位居民站在离地20 m高的阳台上观测到对面小高层房顶的仰角为60°,小高层底部的俯角为45°,那么这栋小高层的高度为 m.
4.在高出海平面200 m的小岛顶上A处,测得位于正西和正东方向的两船的俯角分别是45°与30°,此时两船间的距离为 m.
参考答案
课时4 余弦定理、正弦定理应用举例
自主预习·悟新知
预学忆思
1.用方向角和方位角.
2.方位角:指从正北方向顺时针转到目标方向线的水平角.
方向角:从指定方向到目标方向线所成的水平角.如南偏西60°.
3.S=absin C=bcsin A=acsin B.
4.可以在地球上选两点,与月亮构成三角形,测量地球上两点的距离和这两点看月亮的视角,通过解三角形求得地月的大致距离.
自学检测
1.(1)√ (2)√ (3)√ (4)√
2.A 【解析】在△ABC中,∠ABC=180°-45°-105°=30°,
由=,得AB=100×=50(m).
3.B 【解析】由题图可得∠B=45°,∠BAC=30°,故BC===30(m).
4.30 【解析】
如图所示,AC=15×4=60,
∠BAC=30°,∠B=45°,
在△ABC中,=,
∴BC=30.
故船与灯塔的距离为30 km.
合作探究·提素养
探究1 情境设置
问题1:测量者在点A的同侧,在所在的河岸边选定一点C,测出AC的距离,∠BAC的大小,∠ACB的大小三个量.
问题2:结合图形,需要测出CD的长,∠BCD的大小,∠BDC的大小,就可以计算出BC的长,同理可以计算出AC的长,再算出AB的长.故只需测量出图中CD的长,角α,β,γ,δ的大小.
新知生成
1.(1)线段 (2)基线长度 高
新知运用
例1 (1)+50 (2)a 【解析】(1)在△CAB中,∠ACB=180°-75°-45°=60°,由正弦定理得=,于是BC===(3+)(米).
于是河段的宽度为d=BCsin∠CBA=(3+)×=+50(米).
(2)∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,
∴∠DAC=60°,∴AD=CD=AC=a.
在△BCD中,∠DBC=180°-30°-105°=45°,
∵=,∴BD=CD·=a·=a.
在△ADB中,∵AB2=AD2+BD2-2·AD·BD·cos∠ADB=a2+a2-2×a×a×=a2,∴AB=a,
∴蓝方这两支精锐部队的距离为a.
巩固训练1 C 【解析】根据题意可知,在△ABC中,∠ABC=30°,∠ACB=75°,∠BAC=75°,BC=20 km,
根据正弦定理得,=,
所以AC=·sin∠ABC=·sin 30°=10(-)(km),故选C.
巩固训练2 【解析】在△ACD中,由已知可得∠CAD=30°,所以AC=CD= km.
在△BCD中,由已知可得∠CBD=60°,由正弦定理可得BC==(km).
在△ABC中,由余弦定理可得AB2=AC2+BC2-2·AC·BC·cos∠BCA=5,所以AB= km.
因此施工单位至少应该准备 km长的电线.
探究2 情境设置
问题:设人的位置为A,塔底为B,塔顶为C,过A作BC的垂线,垂足为D,
则∠DAB=30°,∠DAC=62°,BD=15 m,AB===30(m),
所以BC=·sin∠CAB=·sin 92°≈63.9(m),故电视塔的高约为63.9 m.
新知生成
1.仰角 俯角 2.夹角
新知运用
例2 A
【解析】如图,设水柱高度是h m,水柱底端为C,则在△ABC中,A=60°,AC=h,AB=100,BC=h,根据余弦定理得,(h)2=h2+1002-2×h×100×cos 60°,即h2+50h-5 000=0,解得h=50或h=-100(舍去),故水柱的高度是50 m.
巩固训练 811 【解析】如图,过点D作DE∥AC交BC于点E,
因为∠DAC=20°,
所以∠ADE=160°,
于是∠ADB=360°-160°-65°=135°.
又∠BAD=35°-20°=15°,所以∠ABD=30°.
在△ABD中,由正弦定理,
得AB===1 000(m).
在Rt△ABC中,BC=ABsin 35°≈811(m),
所以山的高度约为811 m.
探究3 情境设置
问题:情境图中AB的方向角是北偏东75°,BC的方向角是北偏东32°.
新知生成
1.目标
2.顺时针 [0°,360°)
新知运用
例3 【解析】如图所示.
设经过t小时两船在C点相遇,则在△ABC中,BC=at,AC=at,∠B=180°-60°=120°.由=,得sin∠CAB====.
∵0°<∠CAB<90°,∴∠CAB=30°,∴∠DAC=60°-30°=30°,
∴甲船应沿北偏东30°的方向前进才能最快与乙船相遇.
巩固训练 【解析】设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,则CD=10t海里,BD=10t海里.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos A=(-1)2+22-2(-1)×2×cos 120°=6,
∴BC=海里.
又∵=,∴sin∠ABC===.
又∠ABC是锐角,
∴∠ABC=45°,∴B点在C点的正东方向上,∴∠CBD=90°+30°=120°.
在△BCD中,由正弦定理,得=.
∴sin∠BCD===,∴∠BCD=30°,
∴缉私船应沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,∴∠D=30°.
∴BD=BC,即10t=,∴t=小时≈15分钟,
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
随堂检测·精评价
1.D 【解析】由题意知A=B=30°,所以C=180°-30°-30°=120°.由正弦定理得=,即AB===4(m).
2.B 【解析】如图,d1=,d2=,因为tan 50°>1>tan 40°,所以d120 m,故选B.
3.20(1+) 【解析】如
图,设AB为阳台的高度,CD为小高层的高度,AE为水平线.由题意知AB=20 m,∠DAE=45°,∠CAE=60°,故AE=DE=AB=20 m,CE=AE·tan 60°=20(m),所以CD=20(1+)(m).
4.200(+1) 【解析】过点A作AH⊥BC于点H,
由图易知∠BAH=45°,∠CAH=60°,AH=200 m,则BH=AH=200 m,CH=AH·tan 60°=200(m).故两船距离BC=BH+CH=200(+1)(m).
【学习目标】
1.熟练掌握正、余弦定理.(数学抽象)
2.能够运用正、余弦定理等知识和方法求解距离、高度、角度问题.(数学抽象)
【自主预习】
1.在浩瀚无垠的海面上航行,最重要的是定位和保持航向.阅读教材,看看船只是如何表达位置和航向的
2.方位角和方向角是如何定义的
3.在△ABC中,角A,B,C的对边分别为a,b,c,试写出用两边及夹角表示的三角形面积公式.
4.如何不登月测量地月的大致距离
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)仰角是视线与视线在水平面的射影的夹角. ( )
(2)两点间不可通又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解. ( )
(3)两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解. ( )
(4)高度问题大多通过正(余)弦定理构造直角三角形来解决. ( )
2.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为( ).
A.50 m B.50 m C.25 m D. m
3.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为( ).
A.20 m
B.30 m
C.20 m
D.30 m
4.一船以15 km/h的速度向东行驶,船在A处看到一灯塔B在北偏东60°的方向上,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°的方向上,这时船与灯塔的距离为 km.
【合作探究】
测量距离问题
问题1:如图所示,A,B两点在河的两岸,在点A的一侧,需测出哪些量,可以求出A,B两点的距离
问题2:如图所示,A,B两点都在河的对岸(不可到达),结合图形,需测出哪些量,可以求出A,B两点间的距离
1.基线的概念与选择原则
(1)定义:在测量上,根据测量需要适当确定的 叫作基线.
(2)性质:在测量过程中,要根据实际需要选取合适的 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越 .
2.测量不可到达的两点间的距离,若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;若两点均不可到达,则需用3个三角形才能解决,一般正、余弦定理都要用到.
如图,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A,B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=100米,则该河段的宽度为 米.参考数据:sin 75°=
在某次军事演习中,红方为了准确分析战场形势,在两个相距为a的军事基地C和D测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则蓝方这两支精锐部队的距离是 .参考数据:sin 75°=
【方法总结】三角形中与距离有关的问题的求解策略:
(1)解决三角形中与距离有关的问题时,若在一个三角形中,则直接利用正弦定理、余弦定理求解即可;若所求的线段在多个三角形中,则要根据条件选择适当的三角形,再利用正弦定理、余弦定理求解.
(2)解决三角形中与距离有关的问题的关键是转化为求三角形中的边,分析所解三角形中已知哪些元素,还需要求出哪些元素,灵活应用正弦定理、余弦定理来解决.
如图,货轮在海上以40 km/h的速度由B向C航行,航行的方位角∠NBC=140°,A处有灯塔,方位角∠NBA=110°.在C处观察灯塔A的方位角∠N'CA=35°,由B到C需要航行半小时,则C到灯塔A的距离是( ).参考数据:sin 75°=
A.10 km
B.10 km
C.10(-)km
D.10(+)km
某市电力部门在抗雪救灾的某项重建工程中,需要在A,B两地之间架设高压电线,因地理条件限制,不能直接测量A,B两地的距离.如图,现测量人员在相距 km的C,D两地(假设A,B,C,D在同一平面上),测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,假如考虑到电线的自然下垂和施工损耗等原因,实际所需电线长度大约是A,B距离的倍,则施工单位至少应该准备 km长的电线.参考数据:sin 75°=
测量高度问题
问题:小明要测量底部不能到达的某电视塔的高度.如图,他选定了离地面高度为15 m的一个地点,他测得电视塔底的俯角为30°,塔顶的仰角为62°.由此估测该电视塔的高为多少 (精确到0.1 m)
1.仰角和俯角:与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫 ,目标视线在水平视线下方时叫 (如图所示).
视角:从眼睛的中心向物体两端所引的两条直线的 ,如图所示,视角50°指的是观察该物体的两端视线张开的角度.
一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的A处测得水柱顶端的仰角为45°,沿A向北偏东30°方向前进100 m到达B处,在B处测得水柱顶端的仰角为30°,则水柱的高度是( ).
A.50 m B.100 m
C.120 m D.150 m
【方法总结】解题思路
某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1 000 m后到达D处,又测得山顶B的仰角为65°,则山的高度约为 m.(精确到1 m,参考数据:≈1.414,sin 35°≈0.574)
测量角度问题
请结合下图,探究下面的问题.
问题:你能用方向角表述图中的角吗
1.方向角
从指定方向线到 方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°(如图所示).
2.方位角
从正北方向 转到目标方向线所成的水平角.如点B的方位角为α(如图所示).
方位角的取值范围: .
甲船在A点发现乙船在北偏东60°的B处,乙船以a海里/时的速度向北行驶,已知甲船的速度是a海里/时,问甲船应沿什么方向前进才能最快与乙船相遇
【方法总结】运用正弦定理、余弦定理解决实际问题的基本步骤:
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形).
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型.
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解.
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
如图所示,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10海里/时的速度追截走私船,此时走私船正以10海里/时的速度从B处向北偏东30°方向逃窜.问:缉私船应
沿什么方向行驶才能最快截获走私船 并求出所需时间.
【随堂检测】
1.学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为4 m,A=30°,则其跨度AB的长为( ).
A.12 m B.8 m
C.3 m D.4 m
2.身高相同的甲、乙两人在同一地平面上的不同方向观测20 m高的旗杆,甲观测的仰角为50°,乙观测的仰角为40°,用d1,d2分别表示甲、乙两人离旗杆的距离,那么有( ).
A.d1>d2 B.d1
3.某位居民站在离地20 m高的阳台上观测到对面小高层房顶的仰角为60°,小高层底部的俯角为45°,那么这栋小高层的高度为 m.
4.在高出海平面200 m的小岛顶上A处,测得位于正西和正东方向的两船的俯角分别是45°与30°,此时两船间的距离为 m.
参考答案
课时4 余弦定理、正弦定理应用举例
自主预习·悟新知
预学忆思
1.用方向角和方位角.
2.方位角:指从正北方向顺时针转到目标方向线的水平角.
方向角:从指定方向到目标方向线所成的水平角.如南偏西60°.
3.S=absin C=bcsin A=acsin B.
4.可以在地球上选两点,与月亮构成三角形,测量地球上两点的距离和这两点看月亮的视角,通过解三角形求得地月的大致距离.
自学检测
1.(1)√ (2)√ (3)√ (4)√
2.A 【解析】在△ABC中,∠ABC=180°-45°-105°=30°,
由=,得AB=100×=50(m).
3.B 【解析】由题图可得∠B=45°,∠BAC=30°,故BC===30(m).
4.30 【解析】
如图所示,AC=15×4=60,
∠BAC=30°,∠B=45°,
在△ABC中,=,
∴BC=30.
故船与灯塔的距离为30 km.
合作探究·提素养
探究1 情境设置
问题1:测量者在点A的同侧,在所在的河岸边选定一点C,测出AC的距离,∠BAC的大小,∠ACB的大小三个量.
问题2:结合图形,需要测出CD的长,∠BCD的大小,∠BDC的大小,就可以计算出BC的长,同理可以计算出AC的长,再算出AB的长.故只需测量出图中CD的长,角α,β,γ,δ的大小.
新知生成
1.(1)线段 (2)基线长度 高
新知运用
例1 (1)+50 (2)a 【解析】(1)在△CAB中,∠ACB=180°-75°-45°=60°,由正弦定理得=,于是BC===(3+)(米).
于是河段的宽度为d=BCsin∠CBA=(3+)×=+50(米).
(2)∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,
∴∠DAC=60°,∴AD=CD=AC=a.
在△BCD中,∠DBC=180°-30°-105°=45°,
∵=,∴BD=CD·=a·=a.
在△ADB中,∵AB2=AD2+BD2-2·AD·BD·cos∠ADB=a2+a2-2×a×a×=a2,∴AB=a,
∴蓝方这两支精锐部队的距离为a.
巩固训练1 C 【解析】根据题意可知,在△ABC中,∠ABC=30°,∠ACB=75°,∠BAC=75°,BC=20 km,
根据正弦定理得,=,
所以AC=·sin∠ABC=·sin 30°=10(-)(km),故选C.
巩固训练2 【解析】在△ACD中,由已知可得∠CAD=30°,所以AC=CD= km.
在△BCD中,由已知可得∠CBD=60°,由正弦定理可得BC==(km).
在△ABC中,由余弦定理可得AB2=AC2+BC2-2·AC·BC·cos∠BCA=5,所以AB= km.
因此施工单位至少应该准备 km长的电线.
探究2 情境设置
问题:设人的位置为A,塔底为B,塔顶为C,过A作BC的垂线,垂足为D,
则∠DAB=30°,∠DAC=62°,BD=15 m,AB===30(m),
所以BC=·sin∠CAB=·sin 92°≈63.9(m),故电视塔的高约为63.9 m.
新知生成
1.仰角 俯角 2.夹角
新知运用
例2 A
【解析】如图,设水柱高度是h m,水柱底端为C,则在△ABC中,A=60°,AC=h,AB=100,BC=h,根据余弦定理得,(h)2=h2+1002-2×h×100×cos 60°,即h2+50h-5 000=0,解得h=50或h=-100(舍去),故水柱的高度是50 m.
巩固训练 811 【解析】如图,过点D作DE∥AC交BC于点E,
因为∠DAC=20°,
所以∠ADE=160°,
于是∠ADB=360°-160°-65°=135°.
又∠BAD=35°-20°=15°,所以∠ABD=30°.
在△ABD中,由正弦定理,
得AB===1 000(m).
在Rt△ABC中,BC=ABsin 35°≈811(m),
所以山的高度约为811 m.
探究3 情境设置
问题:情境图中AB的方向角是北偏东75°,BC的方向角是北偏东32°.
新知生成
1.目标
2.顺时针 [0°,360°)
新知运用
例3 【解析】如图所示.
设经过t小时两船在C点相遇,则在△ABC中,BC=at,AC=at,∠B=180°-60°=120°.由=,得sin∠CAB====.
∵0°<∠CAB<90°,∴∠CAB=30°,∴∠DAC=60°-30°=30°,
∴甲船应沿北偏东30°的方向前进才能最快与乙船相遇.
巩固训练 【解析】设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,则CD=10t海里,BD=10t海里.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos A=(-1)2+22-2(-1)×2×cos 120°=6,
∴BC=海里.
又∵=,∴sin∠ABC===.
又∠ABC是锐角,
∴∠ABC=45°,∴B点在C点的正东方向上,∴∠CBD=90°+30°=120°.
在△BCD中,由正弦定理,得=.
∴sin∠BCD===,∴∠BCD=30°,
∴缉私船应沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,∴∠D=30°.
∴BD=BC,即10t=,∴t=小时≈15分钟,
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
随堂检测·精评价
1.D 【解析】由题意知A=B=30°,所以C=180°-30°-30°=120°.由正弦定理得=,即AB===4(m).
2.B 【解析】如图,d1=,d2=,因为tan 50°>1>tan 40°,所以d1
3.20(1+) 【解析】如
图,设AB为阳台的高度,CD为小高层的高度,AE为水平线.由题意知AB=20 m,∠DAE=45°,∠CAE=60°,故AE=DE=AB=20 m,CE=AE·tan 60°=20(m),所以CD=20(1+)(m).
4.200(+1) 【解析】过点A作AH⊥BC于点H,
由图易知∠BAH=45°,∠CAH=60°,AH=200 m,则BH=AH=200 m,CH=AH·tan 60°=200(m).故两船距离BC=BH+CH=200(+1)(m).
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
