7.5 正态分布 同步学案(含答案) 2024-2025学年高二数学人教A版(2019)选择性必修3
文档属性
| 名称 | 7.5 正态分布 同步学案(含答案) 2024-2025学年高二数学人教A版(2019)选择性必修3 |

|
|
| 格式 | docx | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 14:55:15 | ||
图片预览




文档简介
7.5 正态分布
【学习目标】 1.利用实际问题的频率分布直方图,了解正态曲线的特征和正态曲线所表示的意义.(数学抽象) 2.能借助正态曲线理解正态曲线的性质及意义.(数学抽象、直观想象) 3.会根据正态曲线的性质求随机变量在某一区间的概率.(数学运算、数据分析)
【自主预习】
1.正态曲线的函数表达式是什么
2.X服从正态分布如何表示
3.什么是3σ原则
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)正态密度函数中参数μ,σ的意义分别是样本的均值与方差. ( )
(2)正态曲线是单峰的,其与x轴围成的图形的面积是随参数μ,σ的变化而变化的. ( )
(3)正态曲线可以关于y轴对称. ( )
2.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件零件,其长度误差落在区间(3,6)内的概率为( ).(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ≤ξ≤μ+σ)≈68.27%,P(μ-2σ≤ξ≤μ+2σ)≈95.45%)
A.4.56% B.13.59% C.27.18% D.31.74%
3.已知正态分布总体落在区间,+∞内的概率为,那么相应的正态曲线f(x)在x= 时达到最高点.
4.已知随机变量ξ服从正态分布N(0,1),若P(ξ≤1)=0.841 3,求P(-1≤ξ≤0).
【合作探究】
正态曲线
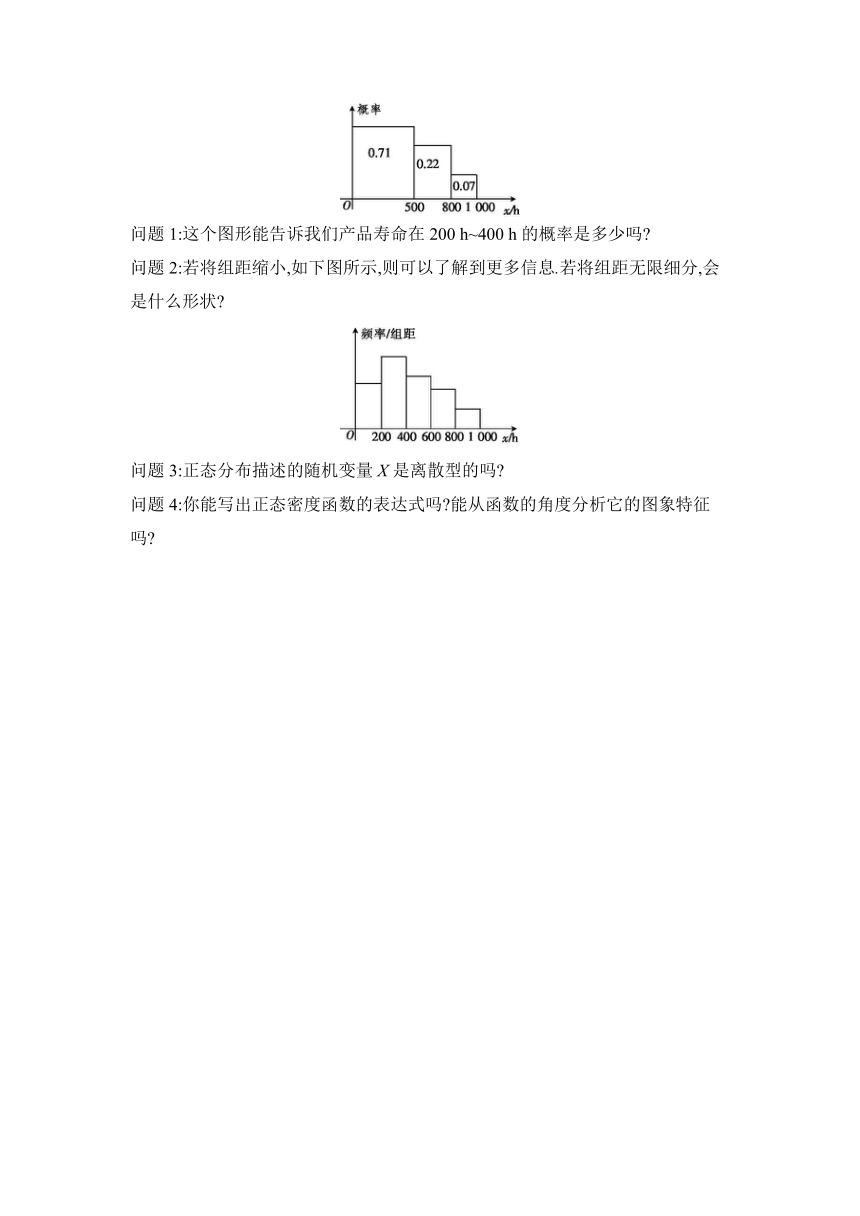
设X表示某产品的寿命(单位:h).人们对该产品有如下的了解:寿命小于500 h的概率为0.71,寿命在500 h~800 h的概率为0.22,寿命在800 h~1 000 h的概率为0.07.由此我们可以画出下图.
问题1:这个图形能告诉我们产品寿命在200 h~400 h的概率是多少吗
问题2:若将组距缩小,如下图所示,则可以了解到更多信息.若将组距无限细分,会是什么形状
问题3:正态分布描述的随机变量X是离散型的吗
问题4:你能写出正态密度函数的表达式吗 能从函数的角度分析它的图象特征吗
1.正态曲线
(1)定义:由误差引起的连续型随机变量其分布密度函数图象如图所示,对应的分布密度函数解析式为f(x)=·,x∈R,其中μ∈R,σ>0为参数,我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线.
(2)误差模型
正态分布是很常见、很重要的连续型随机变量的分布,是刻画误差分布的重要模型,因此也称为误差模型.
2.正态分布
(1)定义:若随机变量X的概率分布函数为f(x),则称随机变量X服从正态分布,记为X~N(μ,σ2).特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
(2)期望与方差:若X~N(μ,σ2),则E(X)= ,D(X)= .
3.正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,关于直线 对称.
(3)曲线在x=μ处达到峰值.
(4)当x<μ时,曲线上升;当x>μ时,曲线下降.当曲线向左、右两边无限延伸时,以x轴为渐近线.
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
(6)当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“高瘦”,表示总体的分布越集中.
一、正态密度函数及正态曲线
如图,这是一条正态曲线,试根据该图象写出其正态密度函数的解析式,并求出总体随机变量的期望和方差.
【方法总结】利用图象求正态密度函数的解析式,应抓住两个实质性特点:一是图象的对称轴为直线x=μ,二是函数的最大值为.这两点确定以后,相应参数μ,σ便确定了,代入f(x)中便可求出相应的解析式.
在正态分布中,当σ=1,μ=0时,正态密度函数为P(x)=(x∈R),则P(x)的最大值为 .
二、正态曲线的性质
某次我市高三教学质量检测中,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,故成绩分布的直方图可视为正态分布),则由曲线可得下列说法中正确的一项是( ).
A.甲科总体的标准差最小
B.丙科总体的平均数最小
C.乙科总体的标准差及平均数都居中
D.甲、乙、丙三科总体的平均数不相同
【方法总结】由正态曲线的性质可以求参数μ,σ:(1)正态曲线是单峰的,它关于直线x=μ对称,由此性质结合图象求μ;(2)正态曲线在x=μ处达到峰值,由此性质结合图象可求σ;(3)由σ的大小区分曲线的“胖瘦”.
(多选题)设随机变量ξ~N(μ,σ2)(σ>0),则( ).
A.正态曲线关于直线x=μ对称
B.正态曲线随着μ的变化而上下波动
C.设随机变量X~N(3,9),则DX=3
D.正态曲线与x轴之间的区域的面积为1
三、正态分布的概率计算
已知随机变量ξ服从正态分布N(3,σ2),且=,则P(3<ξ<5)=( ).
A. B. C. D.
某体育器材厂生产一批篮球,单个篮球的质量Y(单位:克)服从正态分布N(600,4),从这一批篮球中随机抽检300个,则被抽检的篮球的质量不小于596克的个数约为( ).
A.296 B.293 C.252 D.246
3σ原则
问题1:若某工厂生产的圆柱形零件的外直径ε~N(4,0.25),则该圆柱形零件外直径的均值、标准差分别是多少
问题2:某工厂生产的圆柱形零件的外直径ε~N(4,0.25),若零件的外直径在[3.5,4.5]内的为一等品.试问1 000件这种零件中约有多少件一等品
1.正态变量在三个特殊区间内取值的概率如图,正态分布随机变量X在区间[μ-σ,μ+σ](σ>0)上取值的概率为阴影部分的面积.
特别地,(1)P(μ-σ≤X≤μ+σ)≈0.682 7;
(2)P(μ-2σ≤X≤μ+2σ)≈0.954 5;
(3)P(μ-3σ≤X≤μ+3σ)≈0.997 3.
2.3σ原则
随机变量X在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]上取值的概率分别约为68.27%,95.45%,99.73%.而随机变量X在区间[μ-3σ,μ+3σ]以外取值的概率大约只有0.27%,通常认为这种情况在一次试验中几乎不可能发生,是小概率事件.因此,在实际应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,并称之为3σ原则.
设ξ~N(1,22),试求:
(1)P(-1≤ξ≤3);(2)P(3<ξ≤5);(3)P(ξ>5).
【方法总结】求随机变量X在某个区间内取值的概率的方法 (1)利用X落在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]内的概率分别约是0.682 7,0.954 5,0.997 3求解. (2)充分利用正态曲线的对称性及正态曲线与x轴之间的区域面积为1的性质求解:①熟记正态曲线关于直线x=μ对称,从而关于x=μ对称的两区间概率相等;②P(X≤a)=1-P(X>a),P(X≤μ-a)=P(X≥μ+a).
有一批精密零件,其尺寸X(单位:mm)服从正态分布N(20,4).若这批零件共有5 000个,试求:
(1)这批零件中尺寸在18 mm~22 mm的零件所占的百分比.
(2)若规定尺寸在24 mm~26 mm的零件不合格,则这批零件中不合格的零件大约有多少个
【方法总结】 解决此类问题一定要灵活把握3σ原则,将所求概率向P(μ-σ≤ξ≤μ+σ),P(μ-2σ≤ξ≤μ+2σ),P(μ-3σ≤ξ≤μ+3σ)进行转化,然后利用特定值求出相应的概率.同时要充分利用曲线的对称性和曲线与x轴之间的区域面积为1这些特殊性质.
某企业生产一种零部件,其质量指标在(49.6,50.4)内的为优品.技术改造前,该企业生产的该种零部件质量指标服从正态分布N(50,0.16);技术改造后,该企业生产的同种零部件质量指标服从正态分布N(50,0.04).那么该企业生产的这种零部件技术改造后的优品率与技术改造前的优品率之差约为 .(若X~N(μ,σ2),则P(|X-μ|<σ)≈0.682 7,P(|X-μ|<2σ)≈0.954 5,P(|X-μ|<3σ)≈0.997 3)
【随堂检测】
1.以下关于正态密度曲线的说法中,正确的个数是( ).
①曲线都在x轴的上方,左右两侧与x轴无限接近,最终可与x轴相交;
②曲线关于直线x=μ对称;
③曲线呈现“中间高,两边低”的钟形形状;
④曲线与x轴之间的区域的面积为1.
A.1 B.2 C.3 D.4
2.已知正态密度函数f(x)=,则( ).
A.μ=2,σ=3 B.μ=3,σ=2
C.μ=2,σ= D.μ=3,σ=
3.设随机变量ξ服从正态分布N(2,9),若P(ξ>c+1)=P(ξ4.某批待出口的水果罐头,每罐净重X(单位:g)服从正态分布N(184,2.52),求:
(1)随机抽取1罐水果罐头,其净重超过184.5 g的概率;
(2)随机抽取1罐水果罐头,其净重在179 g与189 g之间的概率.
(参考数据:Z~N(0,1),P(Z≤0.2)≈0.579 3,P(Z≤2)≈0.977 2)
参考答案
7.5 正态分布
自主预习·悟新知
预学忆思
1.f(x)=,x∈R.
2.X~N(μ,σ2).其中E(X)=μ,D(X)=σ2.
3.通常认为服从正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
自学检测
1.(1)× (2)× (3)√
2.B 【解析】P(3<ξ<6)=[P(-6<ξ<6)-P(-3≤ξ≤3)]≈×(95.45%-68.27%)=13.59%.故选B.
3. 【解析】由题意可知PX>=PX<,所以正态曲线关于直线x=对称.由正态曲线的性质得,在x=μ=时正态曲线达到最高点.
4.【解析】因为P(ξ≤1)=0.841 3,所以P(ξ>1)=1-0.841 3=0.158 7,所以P(ξ<-1)=0.158 7,所以P(-1≤ξ≤0)=0.5-0.158 7=0.341 3.
合作探究·提素养
探究1 情境设置
问题1:不能.
问题2:若组距无限细分,一般是形状像“钟”的光滑曲线,即正态曲线.
问题3:不是,它是连续的.
问题4:能.正态密度函数的解析式为f(x)=·,x∈R,其中实数μ∈R,σ>0为参数.
由函数表达式可知f(x)>0,且函数f(x)的图象关于直线x=μ对称.
新知生成
2.(2)μ σ2
3.(2)x=μ
新知运用
例1 【解析】由给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值是,所以μ=20.由=,得σ=2.
于是正态密度函数的解析式为f(x)=·,x∈R,
所以总体随机变量的期望μ=20,方差σ2=4.
巩固训练 【解析】令t=-≤0,则f(t)=et在(-∞,0]上单调递增,所以当t=0,即x=0时,P(x)取得最大值,最大值为.
例2 A 【解析】由题中图象可知三科总体的平均数(均值)相等.由正态曲线的性质可知,σ越大,正态曲线越“矮胖”;σ越小,正态曲线越“高瘦”,故三科总体的标准差从小到大依次为甲、乙、丙.故选A.
巩固训练 AD 【解析】由正态曲线的性质知,A,D正确;
正态曲线随着μ的变化而沿着x轴平移,B错误;
设随机变量X~N(3,9),则D(X)=9,
所以DX=×9=1,C错误.故选AD.
例3 C 【解析】由=,及P(ξ<1)=P(ξ>5),P(ξ<5)+P(ξ≥5)=1,
计算可得P(ξ≥5)=,故P(3<ξ<5)=-P(ξ≥5)=-=.
巩固训练 B 【解析】由题意得μ=600,σ==2,
P(Y≥596)=P(Y≥μ-2σ)=0.5+=0.977 25,
0.977 25×300=293.175≈293,所以被抽检的篮球的质量不小于596克的个数约为293.
探究2 情境设置
问题1:零件外直径的均值为4,标准差为0.5.
问题2:P(3.5≤ε≤4.5)=P(μ-σ≤ε≤μ+σ)≈0.682 7,所以1 000件产品中大约有1 000×0.682 7≈683件一等品.
新知运用
例4 【解析】因为ξ~N(1,22),所以μ=1,σ=2.
(1)P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.682 7.
(2)因为P(3<ξ≤5)=P(-3≤ξ<-1),
所以P(3<ξ≤5)=[P(-3≤ξ≤5)-P(-1≤ξ≤3)]
=[P(1-4≤ξ≤1+4)-P(1-2≤ξ≤1+2)]
=[P(μ-2σ≤ξ≤μ+2σ)-P(μ-σ≤ξ≤μ+σ)]
≈×(0.954 5-0.682 7)=0.135 9.
(3)P(ξ>5)=P(ξ<-3)=[1-P(-3≤ξ≤5)]
=[1-P(1-4≤ξ≤1+4)]
=[1-P(μ-2σ≤ξ≤μ+2σ)]
≈×(1-0.954 5)=0.022 75.
例5 【解析】(1)∵X~N(20,4),∴μ=20,σ=2,∴μ-σ=18,μ+σ=22,
∴尺寸在18 mm~22 mm的零件所占的百分比大约是68.27%.
(2)∵μ-3σ=14,μ+3σ=26,μ-2σ=16,μ+2σ=24,
∴尺寸在14 mm~26 mm的零件所占的百分比大约是99.73%,而尺寸在16 mm~24 mm的零件所占的百分比大约是95.45%,
∴尺寸在24 mm~26 mm的零件所占的百分比大约是=2.14%,
∴尺寸在24 mm~26 mm的零件大约有5 000×2.14%=107(个).
∴这批零件中不合格的零件大约有107个.
巩固训练 0.271 8 【解析】技术改造前,易知μ1=50,σ1=0.4,
则其优品率为P(49.6技术改造后,易知μ2=50,σ2=0.2,
则其优品率为P(49.6所以优品率之差约为0.954 5-0.682 7=0.271 8.
随堂检测·精评价
1.C 【解析】由正态密度曲线的特点,易知②③④说法正确.对于①,曲线与x轴不相交,故①错误.
2.C 【解析】由f(x)=,得μ=2,σ=.
3.2 【解析】∵ξ~N(2,9),P(ξ>c+1)=P(ξ∴=2,解得c=2.
4.【解析】(1)P(X>184.5)=P>=P(Z>0.2)=1-P(Z≤0.2)≈1-0.579 3=0.420 7.
故随机抽取1罐水果罐头,其净重超过184.5 g的概率约是0.420 7.
(2)P(179故随机抽取1罐水果罐头,其净重在179 g与189 g之间的概率约为0.954 4.
【学习目标】 1.利用实际问题的频率分布直方图,了解正态曲线的特征和正态曲线所表示的意义.(数学抽象) 2.能借助正态曲线理解正态曲线的性质及意义.(数学抽象、直观想象) 3.会根据正态曲线的性质求随机变量在某一区间的概率.(数学运算、数据分析)
【自主预习】
1.正态曲线的函数表达式是什么
2.X服从正态分布如何表示
3.什么是3σ原则
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)正态密度函数中参数μ,σ的意义分别是样本的均值与方差. ( )
(2)正态曲线是单峰的,其与x轴围成的图形的面积是随参数μ,σ的变化而变化的. ( )
(3)正态曲线可以关于y轴对称. ( )
2.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件零件,其长度误差落在区间(3,6)内的概率为( ).(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ≤ξ≤μ+σ)≈68.27%,P(μ-2σ≤ξ≤μ+2σ)≈95.45%)
A.4.56% B.13.59% C.27.18% D.31.74%
3.已知正态分布总体落在区间,+∞内的概率为,那么相应的正态曲线f(x)在x= 时达到最高点.
4.已知随机变量ξ服从正态分布N(0,1),若P(ξ≤1)=0.841 3,求P(-1≤ξ≤0).
【合作探究】
正态曲线
设X表示某产品的寿命(单位:h).人们对该产品有如下的了解:寿命小于500 h的概率为0.71,寿命在500 h~800 h的概率为0.22,寿命在800 h~1 000 h的概率为0.07.由此我们可以画出下图.
问题1:这个图形能告诉我们产品寿命在200 h~400 h的概率是多少吗
问题2:若将组距缩小,如下图所示,则可以了解到更多信息.若将组距无限细分,会是什么形状
问题3:正态分布描述的随机变量X是离散型的吗
问题4:你能写出正态密度函数的表达式吗 能从函数的角度分析它的图象特征吗
1.正态曲线
(1)定义:由误差引起的连续型随机变量其分布密度函数图象如图所示,对应的分布密度函数解析式为f(x)=·,x∈R,其中μ∈R,σ>0为参数,我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线.
(2)误差模型
正态分布是很常见、很重要的连续型随机变量的分布,是刻画误差分布的重要模型,因此也称为误差模型.
2.正态分布
(1)定义:若随机变量X的概率分布函数为f(x),则称随机变量X服从正态分布,记为X~N(μ,σ2).特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
(2)期望与方差:若X~N(μ,σ2),则E(X)= ,D(X)= .
3.正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,关于直线 对称.
(3)曲线在x=μ处达到峰值.
(4)当x<μ时,曲线上升;当x>μ时,曲线下降.当曲线向左、右两边无限延伸时,以x轴为渐近线.
(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
(6)当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“高瘦”,表示总体的分布越集中.
一、正态密度函数及正态曲线
如图,这是一条正态曲线,试根据该图象写出其正态密度函数的解析式,并求出总体随机变量的期望和方差.
【方法总结】利用图象求正态密度函数的解析式,应抓住两个实质性特点:一是图象的对称轴为直线x=μ,二是函数的最大值为.这两点确定以后,相应参数μ,σ便确定了,代入f(x)中便可求出相应的解析式.
在正态分布中,当σ=1,μ=0时,正态密度函数为P(x)=(x∈R),则P(x)的最大值为 .
二、正态曲线的性质
某次我市高三教学质量检测中,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,故成绩分布的直方图可视为正态分布),则由曲线可得下列说法中正确的一项是( ).
A.甲科总体的标准差最小
B.丙科总体的平均数最小
C.乙科总体的标准差及平均数都居中
D.甲、乙、丙三科总体的平均数不相同
【方法总结】由正态曲线的性质可以求参数μ,σ:(1)正态曲线是单峰的,它关于直线x=μ对称,由此性质结合图象求μ;(2)正态曲线在x=μ处达到峰值,由此性质结合图象可求σ;(3)由σ的大小区分曲线的“胖瘦”.
(多选题)设随机变量ξ~N(μ,σ2)(σ>0),则( ).
A.正态曲线关于直线x=μ对称
B.正态曲线随着μ的变化而上下波动
C.设随机变量X~N(3,9),则DX=3
D.正态曲线与x轴之间的区域的面积为1
三、正态分布的概率计算
已知随机变量ξ服从正态分布N(3,σ2),且=,则P(3<ξ<5)=( ).
A. B. C. D.
某体育器材厂生产一批篮球,单个篮球的质量Y(单位:克)服从正态分布N(600,4),从这一批篮球中随机抽检300个,则被抽检的篮球的质量不小于596克的个数约为( ).
A.296 B.293 C.252 D.246
3σ原则
问题1:若某工厂生产的圆柱形零件的外直径ε~N(4,0.25),则该圆柱形零件外直径的均值、标准差分别是多少
问题2:某工厂生产的圆柱形零件的外直径ε~N(4,0.25),若零件的外直径在[3.5,4.5]内的为一等品.试问1 000件这种零件中约有多少件一等品
1.正态变量在三个特殊区间内取值的概率如图,正态分布随机变量X在区间[μ-σ,μ+σ](σ>0)上取值的概率为阴影部分的面积.
特别地,(1)P(μ-σ≤X≤μ+σ)≈0.682 7;
(2)P(μ-2σ≤X≤μ+2σ)≈0.954 5;
(3)P(μ-3σ≤X≤μ+3σ)≈0.997 3.
2.3σ原则
随机变量X在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]上取值的概率分别约为68.27%,95.45%,99.73%.而随机变量X在区间[μ-3σ,μ+3σ]以外取值的概率大约只有0.27%,通常认为这种情况在一次试验中几乎不可能发生,是小概率事件.因此,在实际应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,并称之为3σ原则.
设ξ~N(1,22),试求:
(1)P(-1≤ξ≤3);(2)P(3<ξ≤5);(3)P(ξ>5).
【方法总结】求随机变量X在某个区间内取值的概率的方法 (1)利用X落在区间[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]内的概率分别约是0.682 7,0.954 5,0.997 3求解. (2)充分利用正态曲线的对称性及正态曲线与x轴之间的区域面积为1的性质求解:①熟记正态曲线关于直线x=μ对称,从而关于x=μ对称的两区间概率相等;②P(X≤a)=1-P(X>a),P(X≤μ-a)=P(X≥μ+a).
有一批精密零件,其尺寸X(单位:mm)服从正态分布N(20,4).若这批零件共有5 000个,试求:
(1)这批零件中尺寸在18 mm~22 mm的零件所占的百分比.
(2)若规定尺寸在24 mm~26 mm的零件不合格,则这批零件中不合格的零件大约有多少个
【方法总结】 解决此类问题一定要灵活把握3σ原则,将所求概率向P(μ-σ≤ξ≤μ+σ),P(μ-2σ≤ξ≤μ+2σ),P(μ-3σ≤ξ≤μ+3σ)进行转化,然后利用特定值求出相应的概率.同时要充分利用曲线的对称性和曲线与x轴之间的区域面积为1这些特殊性质.
某企业生产一种零部件,其质量指标在(49.6,50.4)内的为优品.技术改造前,该企业生产的该种零部件质量指标服从正态分布N(50,0.16);技术改造后,该企业生产的同种零部件质量指标服从正态分布N(50,0.04).那么该企业生产的这种零部件技术改造后的优品率与技术改造前的优品率之差约为 .(若X~N(μ,σ2),则P(|X-μ|<σ)≈0.682 7,P(|X-μ|<2σ)≈0.954 5,P(|X-μ|<3σ)≈0.997 3)
【随堂检测】
1.以下关于正态密度曲线的说法中,正确的个数是( ).
①曲线都在x轴的上方,左右两侧与x轴无限接近,最终可与x轴相交;
②曲线关于直线x=μ对称;
③曲线呈现“中间高,两边低”的钟形形状;
④曲线与x轴之间的区域的面积为1.
A.1 B.2 C.3 D.4
2.已知正态密度函数f(x)=,则( ).
A.μ=2,σ=3 B.μ=3,σ=2
C.μ=2,σ= D.μ=3,σ=
3.设随机变量ξ服从正态分布N(2,9),若P(ξ>c+1)=P(ξ
(1)随机抽取1罐水果罐头,其净重超过184.5 g的概率;
(2)随机抽取1罐水果罐头,其净重在179 g与189 g之间的概率.
(参考数据:Z~N(0,1),P(Z≤0.2)≈0.579 3,P(Z≤2)≈0.977 2)
参考答案
7.5 正态分布
自主预习·悟新知
预学忆思
1.f(x)=,x∈R.
2.X~N(μ,σ2).其中E(X)=μ,D(X)=σ2.
3.通常认为服从正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
自学检测
1.(1)× (2)× (3)√
2.B 【解析】P(3<ξ<6)=[P(-6<ξ<6)-P(-3≤ξ≤3)]≈×(95.45%-68.27%)=13.59%.故选B.
3. 【解析】由题意可知PX>=PX<,所以正态曲线关于直线x=对称.由正态曲线的性质得,在x=μ=时正态曲线达到最高点.
4.【解析】因为P(ξ≤1)=0.841 3,所以P(ξ>1)=1-0.841 3=0.158 7,所以P(ξ<-1)=0.158 7,所以P(-1≤ξ≤0)=0.5-0.158 7=0.341 3.
合作探究·提素养
探究1 情境设置
问题1:不能.
问题2:若组距无限细分,一般是形状像“钟”的光滑曲线,即正态曲线.
问题3:不是,它是连续的.
问题4:能.正态密度函数的解析式为f(x)=·,x∈R,其中实数μ∈R,σ>0为参数.
由函数表达式可知f(x)>0,且函数f(x)的图象关于直线x=μ对称.
新知生成
2.(2)μ σ2
3.(2)x=μ
新知运用
例1 【解析】由给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值是,所以μ=20.由=,得σ=2.
于是正态密度函数的解析式为f(x)=·,x∈R,
所以总体随机变量的期望μ=20,方差σ2=4.
巩固训练 【解析】令t=-≤0,则f(t)=et在(-∞,0]上单调递增,所以当t=0,即x=0时,P(x)取得最大值,最大值为.
例2 A 【解析】由题中图象可知三科总体的平均数(均值)相等.由正态曲线的性质可知,σ越大,正态曲线越“矮胖”;σ越小,正态曲线越“高瘦”,故三科总体的标准差从小到大依次为甲、乙、丙.故选A.
巩固训练 AD 【解析】由正态曲线的性质知,A,D正确;
正态曲线随着μ的变化而沿着x轴平移,B错误;
设随机变量X~N(3,9),则D(X)=9,
所以DX=×9=1,C错误.故选AD.
例3 C 【解析】由=,及P(ξ<1)=P(ξ>5),P(ξ<5)+P(ξ≥5)=1,
计算可得P(ξ≥5)=,故P(3<ξ<5)=-P(ξ≥5)=-=.
巩固训练 B 【解析】由题意得μ=600,σ==2,
P(Y≥596)=P(Y≥μ-2σ)=0.5+=0.977 25,
0.977 25×300=293.175≈293,所以被抽检的篮球的质量不小于596克的个数约为293.
探究2 情境设置
问题1:零件外直径的均值为4,标准差为0.5.
问题2:P(3.5≤ε≤4.5)=P(μ-σ≤ε≤μ+σ)≈0.682 7,所以1 000件产品中大约有1 000×0.682 7≈683件一等品.
新知运用
例4 【解析】因为ξ~N(1,22),所以μ=1,σ=2.
(1)P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.682 7.
(2)因为P(3<ξ≤5)=P(-3≤ξ<-1),
所以P(3<ξ≤5)=[P(-3≤ξ≤5)-P(-1≤ξ≤3)]
=[P(1-4≤ξ≤1+4)-P(1-2≤ξ≤1+2)]
=[P(μ-2σ≤ξ≤μ+2σ)-P(μ-σ≤ξ≤μ+σ)]
≈×(0.954 5-0.682 7)=0.135 9.
(3)P(ξ>5)=P(ξ<-3)=[1-P(-3≤ξ≤5)]
=[1-P(1-4≤ξ≤1+4)]
=[1-P(μ-2σ≤ξ≤μ+2σ)]
≈×(1-0.954 5)=0.022 75.
例5 【解析】(1)∵X~N(20,4),∴μ=20,σ=2,∴μ-σ=18,μ+σ=22,
∴尺寸在18 mm~22 mm的零件所占的百分比大约是68.27%.
(2)∵μ-3σ=14,μ+3σ=26,μ-2σ=16,μ+2σ=24,
∴尺寸在14 mm~26 mm的零件所占的百分比大约是99.73%,而尺寸在16 mm~24 mm的零件所占的百分比大约是95.45%,
∴尺寸在24 mm~26 mm的零件所占的百分比大约是=2.14%,
∴尺寸在24 mm~26 mm的零件大约有5 000×2.14%=107(个).
∴这批零件中不合格的零件大约有107个.
巩固训练 0.271 8 【解析】技术改造前,易知μ1=50,σ1=0.4,
则其优品率为P(49.6
则其优品率为P(49.6
随堂检测·精评价
1.C 【解析】由正态密度曲线的特点,易知②③④说法正确.对于①,曲线与x轴不相交,故①错误.
2.C 【解析】由f(x)=,得μ=2,σ=.
3.2 【解析】∵ξ~N(2,9),P(ξ>c+1)=P(ξ
4.【解析】(1)P(X>184.5)=P>=P(Z>0.2)=1-P(Z≤0.2)≈1-0.579 3=0.420 7.
故随机抽取1罐水果罐头,其净重超过184.5 g的概率约是0.420 7.
(2)P(179
