2.6.1 函数的单调性 学案(含答案) 2024-2025学年高二数学北师大版(2019)选择性必修2
文档属性
| 名称 | 2.6.1 函数的单调性 学案(含答案) 2024-2025学年高二数学北师大版(2019)选择性必修2 |  | |
| 格式 | docx | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 22:18:26 | ||
图片预览



文档简介
2.6.1 函数的单调性
【学习目标】
1.理解导数与函数的单调性的关系.(数学抽象、逻辑推理、直观想象)
2.掌握利用导数判断函数单调性的方法.(数学抽象、逻辑推理)
3.会用导数求函数的单调区间.(逻辑推理、数学运算)
【自主预习】
1.我们知道判断函数y=x2的单调性可以用定义法、图象法,对于函数y=x3-3x,如何判断它的单调性呢
2.对于可导函数f(x),f(x)的单调性与它的导数有什么关系
3.如何利用导数求函数f(x)的单调区间
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)若函数f(x)在(a,b)上单调递增,则一定有f'(x)>0. ( )
(2)若 x∈(a,b),f'(x)>0,则函数f(x)在(a,b)上单调递增. ( )
(3)若 x∈(a,b),f'(x)=0,则函数f(x)在(a,b)上一定不单调. ( )
(4)已知f(x)是定义在R上的可导函数,若 x≥a,f(x)≥f(a),则f'(a)≥0. ( )
2.下列函数中,在(0,+∞)上单调递增的是( ).
A.y=sin x B.y=xex
C.y=x3-x D.y=ln x-x
3.已知函数f(x)的导函数y=f'(x)的图象如图所示,则函数f(x)的单调递增区间为 .
4.证明:函数f(x)=x+在(0,1]上单调递减.
【合作探究】
求函数的单调区间
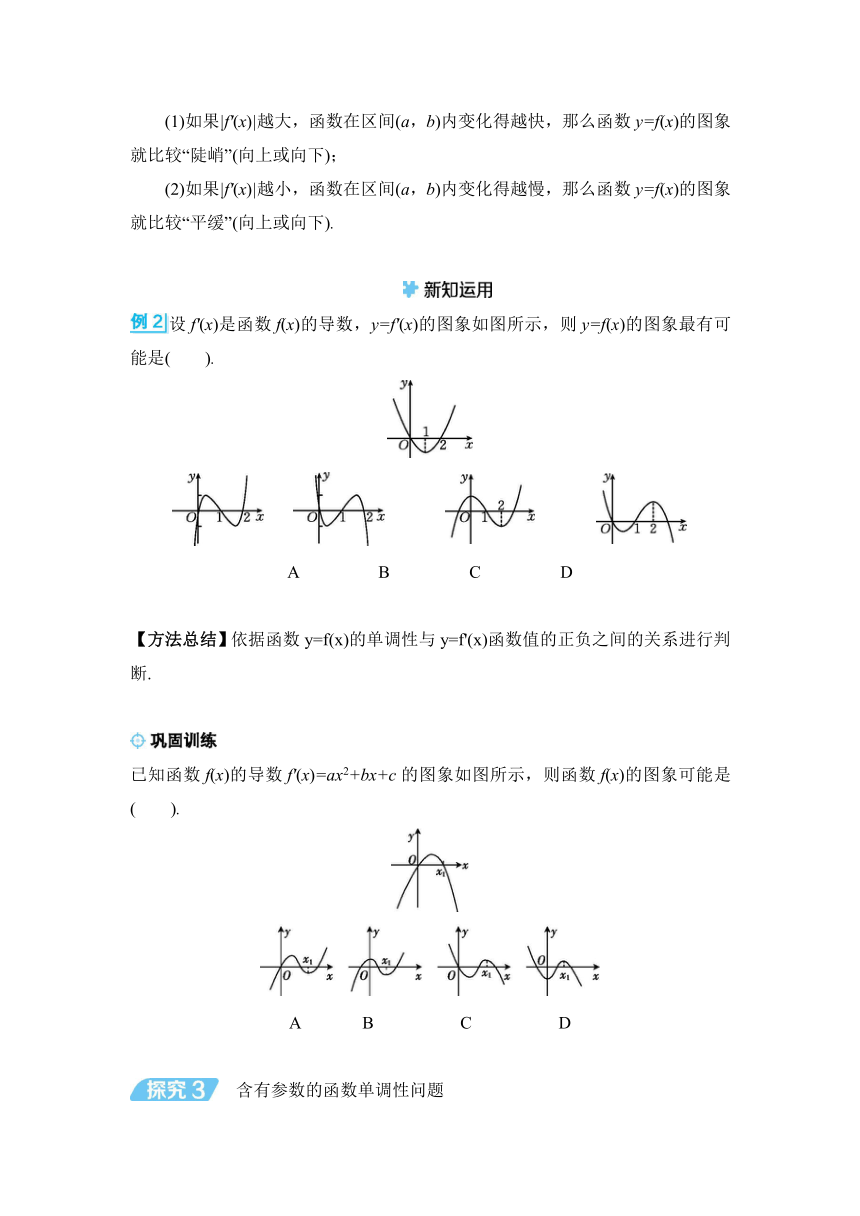
某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x-1.5x2.
问题1:作出这个函数的图象,求出这个函数的导数y',你能发现函数的单调性与导数的正负有什么关系吗
问题2:观察下面一些函数的图象,探究函数的单调性和导数正负的关系.
导数的符号与函数的单调性之间具有如下的关系:
(1)若在某个区间上,函数y=f(x)的导数f'(x)>0,则在这个区间上,函数y=f(x)单调递增;
(2)若在某个区间上,函数y=f(x)的导数f'(x)<0,则在这个区间上,函数y=f(x)单调递减;
(3)若在某个区间上,f'(x)≥0,且只在有限个点为0,则在这个区间上,函数y=f(x)单调递增;若在某个区间上,f'(x)≤0,且只在有限个点为0,则在这个区间上,函数y=f(x)单调递减.
求函数f(x)=2x3-6x2+7的单调区间.
【方法总结】先求f'(x),再解不等式f'(x)>0和f'(x)<0,即可分别得到函数f(x)的单调递增区间和单调递减区间.
求下列函数的单调区间:
(1)f(x)=x+sin x,x∈(0,2π);(2)f(x)=2x-ln x.
函数与其导数图象间的关系
问题1:结合函数图象,如何从导数的角度解释函数增减快慢的情况
问题2:若函数f(x)在(a,b)上满足f'(x)>0(或f'(x)<0),则f(x)在(a,b)上具备什么样的单调性
问题3:若函数f(x)为可导函数,且在区间(a,b)上单调递增(减),则f'(x)满足什么条件
函数单调性与导数值大小的关系
一般地,设可导函数y=f(x),在区间(a,b)内,
(1)如果|f'(x)|越大,函数在区间(a,b)内变化得越快,那么函数y=f(x)的图象就比较“陡峭”(向上或向下);
(2)如果|f'(x)|越小,函数在区间(a,b)内变化得越慢,那么函数y=f(x)的图象就比较“平缓”(向上或向下).
设f'(x)是函数f(x)的导数,y=f'(x)的图象如图所示,则y=f(x)的图象最有可能是( ).
A B C D
【方法总结】依据函数y=f(x)的单调性与y=f'(x)函数值的正负之间的关系进行判断.
已知函数f(x)的导数f'(x)=ax2+bx+c的图象如图所示,则函数f(x)的图象可能是( ).
A B C D
含有参数的函数单调性问题
如图所示的S形公路,可近似地用函数f(x)=ax3+3x2-x+1(a≠0)来表示.
问题:如果f(x)在R上单调递减,求实数a的取值范围.
1.f(x)的解析式中含有参数,讨论f(x)的单调性时,应注意不等式f'(x)≥0(或f'(x)≤0)的解集与参数是否相关,相关时要分类讨论.
2.f(x)的解析式中含有参数,已知f(x)在定义域内单调递增(或减),则f'(x)≥0(或f'(x)≤0)在f(x)的定义域内恒成立,有时借助数形结合法求解.
3.已知f(x)(f(x)的解析式中含有参数)在某区间上单调,求参数的值或取值范围时,所给增(或减)区间应是f(x)的增(或减)区间的子集.
4.已知f(x)的单调区间,求f(x)中含有的参数值时,已知单调区间的端点应是f'(x)≥0(f'(x)≤0)解集的分界点.
已知函数f(x)=-x+aln x,讨论f(x)的单调性.
【方法总结】先求定义域,再求导数f'(x),根据x的取值范围讨论导数在定义域上的符号即可.
若函数f(x)=x3-ax2+(a-1)x+1在区间(1,4)上单调递减,在区间(6,+∞)上单调递增,试求实数a的取值范围.
函数单调性的应用
已知函数f(x)的定义域为(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<-xf'(x),则不等式f(x+1)>(x-1)·f(x2-1)的解集是( ).
A.(0,1) B.(2,+∞) C.(1,2) D.(1,+∞)
【方法总结】用函数的单调性比较大小或解不等式时常采用构造函数的方法,常见的构造函数有
(1)对于f'(x)>g'(x),构造h(x)=f(x)-g(x).
(2)对于f'(x)+g'(x)>0,构造h(x)=f(x)+g(x).
(3)对于f'(x)+f(x)>0,构造h(x)=exf(x).
(4)对于f'(x)>f(x),构造h(x)=.
(5)对于xf'(x)+f(x)>0,构造h(x)=xf(x).
(6)对于xf'(x)-f(x)>0,构造h(x)=(注意讨论x=0的情况).
已知f(x)为R上的可导函数,其导函数为f'(x),且对于任意的x∈R,均有f(x)+f'(x)>0,则( ).
A.e-2 021f(-2 021)f(0)
B.e-2 021f(-2 021)C.e-2 021f(-2 021)>f(0),e2 021f(2 021)>f(0)
D.e-2 021f(-2 021)>f(0),e2 021f(2 021)【随堂检测】
1.函数f(x)=2x-sin x在R上是( ).
A.增函数 B.减函数 C.先增后减 D.不确定
2.定义在R上的函数f(x),若(x-1)·f'(x)<0,则( ).
A.f(0)+f(2)>2f(1) B.f(0)+f(2)=2f(1)
C.f(0)+f(2)<2f(1) D.f(0)+f(2)与2f(1)的大小关系不确定
3.已知函数y=f(x)的图象如图所示,则y=f'(x)的图象可能是( ).
A B C D
4.函数f(x)=3+xln x的单调递增区间是 .
5.已知函数f(x)=x3-x2-x+2.
(1)求曲线f(x)在点(2,f(2))处的切线方程;
(2)求f(x)的单调区间.
参考答案
2.6.1 函数的单调性
自主预习·悟新知
预学忆思
1.通过前面的学习,我们可以通过研究函数的导数来判断它的单调性.
2.在区间(a,b)上,如果f'(x)>0,那么函数y=f(x)在区间(a,b)上单调递增;在区间(a,b)上,如果f'(x)<0,那么函数y=f(x)在区间(a,b)上单调递减.
3.先求定义域.令f'(x)>0,结合定义域得单调递增区间;令f'(x)<0,结合定义域得单调递减区间.
自学检测
1.(1)× (2)√ (3)× (4)√
2.B 【解析】(sin x)'=cos x,(xex)'=ex+xex=(1+x)ex,(x3-x)'=3x2-1,(ln x-x)'=-1,当x∈(0,+∞)时,只有(xex)'=(1+x)ex>0恒成立.
3.[-1,0]和[2,+∞) 【解析】∵当-1≤x≤0或x≥2时,f'(x)≥0,
∴函数f(x)的单调递增区间为[-1,0]和[2,+∞).
4.【解析】f'(x)=1-=,∵x∈(0,1],∴x2-1≤0(当且仅当x=1时,等号成立),
∴f'(x)≤0,∴f(x)=x+在(0,1]上单调递减.
合作探究·提素养
探究1 情境设置
问题1:
函数y=60x-1.5x2的图象如图所示,y'=60-3x.在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.
问题2:图象(1)中,在区间(-∞,+∞)上,y'=1>0,y=x单调递增;
图象(2)中,在区间(-∞,0)上,y'=2x<0,y=x2单调递减,在区间(0,+∞)上,y'=2x>0,y=x2单调递增;
图象(3)中,在区间(-∞,+∞)上,y'=3x2≥0,y=x3单调递增;
图象(4)中,在区间(-∞,0),(0,+∞)上,y'=-<0,y=单调递减.
新知运用
例1 【解析】由题可知,f'(x)=6x2-12x.
令f'(x)>0,解得x>2或x<0,
所以当x∈(-∞,0)或x∈(2,+∞)时,f'(x)>0,函数f(x)单调递增;
令f'(x)<0,解得0所以当x∈(0,2)时,f'(x)<0,函数f(x)单调递减.
综上所述,函数f(x)=2x3-6x2+7的单调递增区间为(-∞,0)和(2,+∞),单调递减区间为(0,2).
巩固训练 【解析】(1)由题意知,f'(x)=+cos x,令f'(x)>0,得+cos x>0,即cos x>-.
∵x∈(0,2π),∴0同理,令f'(x)<0,得∴该函数的单调递增区间为0,,,2π;单调递减区间为,.
(2)函数f(x)的定义域为(0,+∞),f'(x)=2-.
令2->0,解得x>;令2-<0,解得0∴该函数的单调递增区间为,+∞,单调递减区间为0,.
探究2 情境设置
问题1:一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.
如图所示,函数y=f(x)在(0,b)或(a,0)内的图象“陡峭”,在(b,+∞)或(-∞,a)内的图象“平缓”.
问题2:若f'(x)>0,则f(x)在(a,b)上单调递增;若f'(x)<0,则f(x)在(a,b)上单调递减.
问题3:f'(x)≥0(或f'(x)≤0).
新知运用
例2 C 【解析】由导函数的图象可得,当x<0时,f'(x)>0,函数f(x)单调递增;
当0当x>2时,f'(x)>0,函数f(x)单调递增.
只有C选项的图象符合.故选C.
巩固训练 D 【解析】观察导数f'(x)的图象可知,当x<0或x>x1时,导数f'(x)<0,即函数f(x)在(-∞,0)和(x1,+∞)上单调递减;当00,即函数f(x)在(0,x1)上单调递增.故选D.
探究3 情境设置
问题:f'(x)=3ax2+6x-1,
由题意得3ax2+6x-1≤0在R上恒成立.
当a≠0时,由题意得解得a≤-3.
故实数a的取值范围是(-∞,-3].
新知运用
例3 【解析】f(x)的定义域为(0,+∞),
f'(x)=--1+=-.
①若a≤2,则f'(x)≤0,当且仅当a=2,x=1时,f'(x)=0,所以f(x)在(0,+∞)上单调递减.
②若a>2,令f'(x)=0,得x=或x=.
当x∈0,∪,+∞时,f'(x)<0;
当x∈,时,f'(x)>0.
所以f(x)在0,,,+∞上单调递减,在,上单调递增.
综上所述,当a∈(-∞,2]时,f(x)在(0,+∞)上单调递减;当a∈(2,+∞)时,f(x)在0,,,+∞上单调递减,在,上单调递增.
巩固训练 【解析】由题意得,f'(x)=x2-ax+a-1=(x-1)[x-(a-1)],令f'(x)=0,得x=1或x=a-1.因为函数f(x)在区间(1,4)上单调递减,所以当x∈(1,4)时,f'(x)≤0.又因为函数f(x)在区间(6,+∞)上单调递增,所以当x∈(6,+∞)时,f'(x)≥0,所以4≤a-1≤6,解得5≤a≤7,即实数a的取值范围为[5,7].
探究4
例4 B 【解析】构造函数y=xf(x),x∈(0,+∞),
则y'=f(x)+xf'(x)<0,
所以函数y=xf(x)在(0,+∞)上单调递减.
又因为f(x+1)>(x-1)f(x2-1),
所以(x+1)f(x+1)>(x2-1)f(x2-1),
所以x+10,x+1>0,
解得x>2,
所以不等式f(x+1)>(x-1)f(x2-1)的解集是(2,+∞).故选B.
巩固训练 A 【解析】构造函数h(x)=exf(x),
则h'(x)=exf(x)+exf'(x)=ex[f(x)+f'(x)]>0,
所以函数h(x)在R上单调递增,
故h(-2 021)同理,h(2 021)>h(0),即e2 021f(2 021)>f(0).故选A.
随堂检测·精评价
1.A 【解析】f'(x)=2-cos x,∵cos x≤1,
∴f'(x)>0,∴f(x)在R上是增函数.
2.C 【解析】当x>1时,f'(x)<0,f(x)单调递减,
∴f(2)当x<1时,f'(x)>0,f(x)单调递增,
∴f(0)因此f(0)+f(2)<2f(1).
3.D 【解析】由f(x)的图象可知,f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,∴在(0,+∞)上f'(x)<0,在(-∞,0)上f'(x)>0.故选D.
4.,+∞ 【解析】函数f(x)的定义域为(0,+∞),f'(x)=ln x+1,令f'(x)>0,即ln x+1>0,得x>,故函数f(x)的单调递增区间为,+∞.
5.【解析】(1)∵f(x)=x3-x2-x+2,∴f'(x)=3x2-2x-1,∴f'(2)=7.
又f(2)=4,∴曲线f(x)在点(2,4)处的切线方程为y-4=7(x-2),即7x-y-10=0.
(2)∵f'(x)=3x2-2x-1=(x-1)(3x+1),
∴当x∈-∞,-∪(1,+∞)时,f'(x)>0;当x∈-,1时,f'(x)<0.
故f(x)的单调递增区间为-∞,-,(1,+∞),单调递减区间为-,1.
【学习目标】
1.理解导数与函数的单调性的关系.(数学抽象、逻辑推理、直观想象)
2.掌握利用导数判断函数单调性的方法.(数学抽象、逻辑推理)
3.会用导数求函数的单调区间.(逻辑推理、数学运算)
【自主预习】
1.我们知道判断函数y=x2的单调性可以用定义法、图象法,对于函数y=x3-3x,如何判断它的单调性呢
2.对于可导函数f(x),f(x)的单调性与它的导数有什么关系
3.如何利用导数求函数f(x)的单调区间
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)若函数f(x)在(a,b)上单调递增,则一定有f'(x)>0. ( )
(2)若 x∈(a,b),f'(x)>0,则函数f(x)在(a,b)上单调递增. ( )
(3)若 x∈(a,b),f'(x)=0,则函数f(x)在(a,b)上一定不单调. ( )
(4)已知f(x)是定义在R上的可导函数,若 x≥a,f(x)≥f(a),则f'(a)≥0. ( )
2.下列函数中,在(0,+∞)上单调递增的是( ).
A.y=sin x B.y=xex
C.y=x3-x D.y=ln x-x
3.已知函数f(x)的导函数y=f'(x)的图象如图所示,则函数f(x)的单调递增区间为 .
4.证明:函数f(x)=x+在(0,1]上单调递减.
【合作探究】
求函数的单调区间
某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x-1.5x2.
问题1:作出这个函数的图象,求出这个函数的导数y',你能发现函数的单调性与导数的正负有什么关系吗
问题2:观察下面一些函数的图象,探究函数的单调性和导数正负的关系.
导数的符号与函数的单调性之间具有如下的关系:
(1)若在某个区间上,函数y=f(x)的导数f'(x)>0,则在这个区间上,函数y=f(x)单调递增;
(2)若在某个区间上,函数y=f(x)的导数f'(x)<0,则在这个区间上,函数y=f(x)单调递减;
(3)若在某个区间上,f'(x)≥0,且只在有限个点为0,则在这个区间上,函数y=f(x)单调递增;若在某个区间上,f'(x)≤0,且只在有限个点为0,则在这个区间上,函数y=f(x)单调递减.
求函数f(x)=2x3-6x2+7的单调区间.
【方法总结】先求f'(x),再解不等式f'(x)>0和f'(x)<0,即可分别得到函数f(x)的单调递增区间和单调递减区间.
求下列函数的单调区间:
(1)f(x)=x+sin x,x∈(0,2π);(2)f(x)=2x-ln x.
函数与其导数图象间的关系
问题1:结合函数图象,如何从导数的角度解释函数增减快慢的情况
问题2:若函数f(x)在(a,b)上满足f'(x)>0(或f'(x)<0),则f(x)在(a,b)上具备什么样的单调性
问题3:若函数f(x)为可导函数,且在区间(a,b)上单调递增(减),则f'(x)满足什么条件
函数单调性与导数值大小的关系
一般地,设可导函数y=f(x),在区间(a,b)内,
(1)如果|f'(x)|越大,函数在区间(a,b)内变化得越快,那么函数y=f(x)的图象就比较“陡峭”(向上或向下);
(2)如果|f'(x)|越小,函数在区间(a,b)内变化得越慢,那么函数y=f(x)的图象就比较“平缓”(向上或向下).
设f'(x)是函数f(x)的导数,y=f'(x)的图象如图所示,则y=f(x)的图象最有可能是( ).
A B C D
【方法总结】依据函数y=f(x)的单调性与y=f'(x)函数值的正负之间的关系进行判断.
已知函数f(x)的导数f'(x)=ax2+bx+c的图象如图所示,则函数f(x)的图象可能是( ).
A B C D
含有参数的函数单调性问题
如图所示的S形公路,可近似地用函数f(x)=ax3+3x2-x+1(a≠0)来表示.
问题:如果f(x)在R上单调递减,求实数a的取值范围.
1.f(x)的解析式中含有参数,讨论f(x)的单调性时,应注意不等式f'(x)≥0(或f'(x)≤0)的解集与参数是否相关,相关时要分类讨论.
2.f(x)的解析式中含有参数,已知f(x)在定义域内单调递增(或减),则f'(x)≥0(或f'(x)≤0)在f(x)的定义域内恒成立,有时借助数形结合法求解.
3.已知f(x)(f(x)的解析式中含有参数)在某区间上单调,求参数的值或取值范围时,所给增(或减)区间应是f(x)的增(或减)区间的子集.
4.已知f(x)的单调区间,求f(x)中含有的参数值时,已知单调区间的端点应是f'(x)≥0(f'(x)≤0)解集的分界点.
已知函数f(x)=-x+aln x,讨论f(x)的单调性.
【方法总结】先求定义域,再求导数f'(x),根据x的取值范围讨论导数在定义域上的符号即可.
若函数f(x)=x3-ax2+(a-1)x+1在区间(1,4)上单调递减,在区间(6,+∞)上单调递增,试求实数a的取值范围.
函数单调性的应用
已知函数f(x)的定义域为(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<-xf'(x),则不等式f(x+1)>(x-1)·f(x2-1)的解集是( ).
A.(0,1) B.(2,+∞) C.(1,2) D.(1,+∞)
【方法总结】用函数的单调性比较大小或解不等式时常采用构造函数的方法,常见的构造函数有
(1)对于f'(x)>g'(x),构造h(x)=f(x)-g(x).
(2)对于f'(x)+g'(x)>0,构造h(x)=f(x)+g(x).
(3)对于f'(x)+f(x)>0,构造h(x)=exf(x).
(4)对于f'(x)>f(x),构造h(x)=.
(5)对于xf'(x)+f(x)>0,构造h(x)=xf(x).
(6)对于xf'(x)-f(x)>0,构造h(x)=(注意讨论x=0的情况).
已知f(x)为R上的可导函数,其导函数为f'(x),且对于任意的x∈R,均有f(x)+f'(x)>0,则( ).
A.e-2 021f(-2 021)
B.e-2 021f(-2 021)
D.e-2 021f(-2 021)>f(0),e2 021f(2 021)
1.函数f(x)=2x-sin x在R上是( ).
A.增函数 B.减函数 C.先增后减 D.不确定
2.定义在R上的函数f(x),若(x-1)·f'(x)<0,则( ).
A.f(0)+f(2)>2f(1) B.f(0)+f(2)=2f(1)
C.f(0)+f(2)<2f(1) D.f(0)+f(2)与2f(1)的大小关系不确定
3.已知函数y=f(x)的图象如图所示,则y=f'(x)的图象可能是( ).
A B C D
4.函数f(x)=3+xln x的单调递增区间是 .
5.已知函数f(x)=x3-x2-x+2.
(1)求曲线f(x)在点(2,f(2))处的切线方程;
(2)求f(x)的单调区间.
参考答案
2.6.1 函数的单调性
自主预习·悟新知
预学忆思
1.通过前面的学习,我们可以通过研究函数的导数来判断它的单调性.
2.在区间(a,b)上,如果f'(x)>0,那么函数y=f(x)在区间(a,b)上单调递增;在区间(a,b)上,如果f'(x)<0,那么函数y=f(x)在区间(a,b)上单调递减.
3.先求定义域.令f'(x)>0,结合定义域得单调递增区间;令f'(x)<0,结合定义域得单调递减区间.
自学检测
1.(1)× (2)√ (3)× (4)√
2.B 【解析】(sin x)'=cos x,(xex)'=ex+xex=(1+x)ex,(x3-x)'=3x2-1,(ln x-x)'=-1,当x∈(0,+∞)时,只有(xex)'=(1+x)ex>0恒成立.
3.[-1,0]和[2,+∞) 【解析】∵当-1≤x≤0或x≥2时,f'(x)≥0,
∴函数f(x)的单调递增区间为[-1,0]和[2,+∞).
4.【解析】f'(x)=1-=,∵x∈(0,1],∴x2-1≤0(当且仅当x=1时,等号成立),
∴f'(x)≤0,∴f(x)=x+在(0,1]上单调递减.
合作探究·提素养
探究1 情境设置
问题1:
函数y=60x-1.5x2的图象如图所示,y'=60-3x.在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.
问题2:图象(1)中,在区间(-∞,+∞)上,y'=1>0,y=x单调递增;
图象(2)中,在区间(-∞,0)上,y'=2x<0,y=x2单调递减,在区间(0,+∞)上,y'=2x>0,y=x2单调递增;
图象(3)中,在区间(-∞,+∞)上,y'=3x2≥0,y=x3单调递增;
图象(4)中,在区间(-∞,0),(0,+∞)上,y'=-<0,y=单调递减.
新知运用
例1 【解析】由题可知,f'(x)=6x2-12x.
令f'(x)>0,解得x>2或x<0,
所以当x∈(-∞,0)或x∈(2,+∞)时,f'(x)>0,函数f(x)单调递增;
令f'(x)<0,解得0
综上所述,函数f(x)=2x3-6x2+7的单调递增区间为(-∞,0)和(2,+∞),单调递减区间为(0,2).
巩固训练 【解析】(1)由题意知,f'(x)=+cos x,令f'(x)>0,得+cos x>0,即cos x>-.
∵x∈(0,2π),∴0
(2)函数f(x)的定义域为(0,+∞),f'(x)=2-.
令2->0,解得x>;令2-<0,解得0
探究2 情境设置
问题1:一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.
如图所示,函数y=f(x)在(0,b)或(a,0)内的图象“陡峭”,在(b,+∞)或(-∞,a)内的图象“平缓”.
问题2:若f'(x)>0,则f(x)在(a,b)上单调递增;若f'(x)<0,则f(x)在(a,b)上单调递减.
问题3:f'(x)≥0(或f'(x)≤0).
新知运用
例2 C 【解析】由导函数的图象可得,当x<0时,f'(x)>0,函数f(x)单调递增;
当0
只有C选项的图象符合.故选C.
巩固训练 D 【解析】观察导数f'(x)的图象可知,当x<0或x>x1时,导数f'(x)<0,即函数f(x)在(-∞,0)和(x1,+∞)上单调递减;当0
探究3 情境设置
问题:f'(x)=3ax2+6x-1,
由题意得3ax2+6x-1≤0在R上恒成立.
当a≠0时,由题意得解得a≤-3.
故实数a的取值范围是(-∞,-3].
新知运用
例3 【解析】f(x)的定义域为(0,+∞),
f'(x)=--1+=-.
①若a≤2,则f'(x)≤0,当且仅当a=2,x=1时,f'(x)=0,所以f(x)在(0,+∞)上单调递减.
②若a>2,令f'(x)=0,得x=或x=.
当x∈0,∪,+∞时,f'(x)<0;
当x∈,时,f'(x)>0.
所以f(x)在0,,,+∞上单调递减,在,上单调递增.
综上所述,当a∈(-∞,2]时,f(x)在(0,+∞)上单调递减;当a∈(2,+∞)时,f(x)在0,,,+∞上单调递减,在,上单调递增.
巩固训练 【解析】由题意得,f'(x)=x2-ax+a-1=(x-1)[x-(a-1)],令f'(x)=0,得x=1或x=a-1.因为函数f(x)在区间(1,4)上单调递减,所以当x∈(1,4)时,f'(x)≤0.又因为函数f(x)在区间(6,+∞)上单调递增,所以当x∈(6,+∞)时,f'(x)≥0,所以4≤a-1≤6,解得5≤a≤7,即实数a的取值范围为[5,7].
探究4
例4 B 【解析】构造函数y=xf(x),x∈(0,+∞),
则y'=f(x)+xf'(x)<0,
所以函数y=xf(x)在(0,+∞)上单调递减.
又因为f(x+1)>(x-1)f(x2-1),
所以(x+1)f(x+1)>(x2-1)f(x2-1),
所以x+1
解得x>2,
所以不等式f(x+1)>(x-1)f(x2-1)的解集是(2,+∞).故选B.
巩固训练 A 【解析】构造函数h(x)=exf(x),
则h'(x)=exf(x)+exf'(x)=ex[f(x)+f'(x)]>0,
所以函数h(x)在R上单调递增,
故h(-2 021)
随堂检测·精评价
1.A 【解析】f'(x)=2-cos x,∵cos x≤1,
∴f'(x)>0,∴f(x)在R上是增函数.
2.C 【解析】当x>1时,f'(x)<0,f(x)单调递减,
∴f(2)
∴f(0)
3.D 【解析】由f(x)的图象可知,f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,∴在(0,+∞)上f'(x)<0,在(-∞,0)上f'(x)>0.故选D.
4.,+∞ 【解析】函数f(x)的定义域为(0,+∞),f'(x)=ln x+1,令f'(x)>0,即ln x+1>0,得x>,故函数f(x)的单调递增区间为,+∞.
5.【解析】(1)∵f(x)=x3-x2-x+2,∴f'(x)=3x2-2x-1,∴f'(2)=7.
又f(2)=4,∴曲线f(x)在点(2,4)处的切线方程为y-4=7(x-2),即7x-y-10=0.
(2)∵f'(x)=3x2-2x-1=(x-1)(3x+1),
∴当x∈-∞,-∪(1,+∞)时,f'(x)>0;当x∈-,1时,f'(x)<0.
故f(x)的单调递增区间为-∞,-,(1,+∞),单调递减区间为-,1.
同课章节目录
