2025年九年级中考数学三轮冲刺练习二次函数中相似三角形存在性问题练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习二次函数中相似三角形存在性问题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:07:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习二次函数中相似三角形存在性问题练习
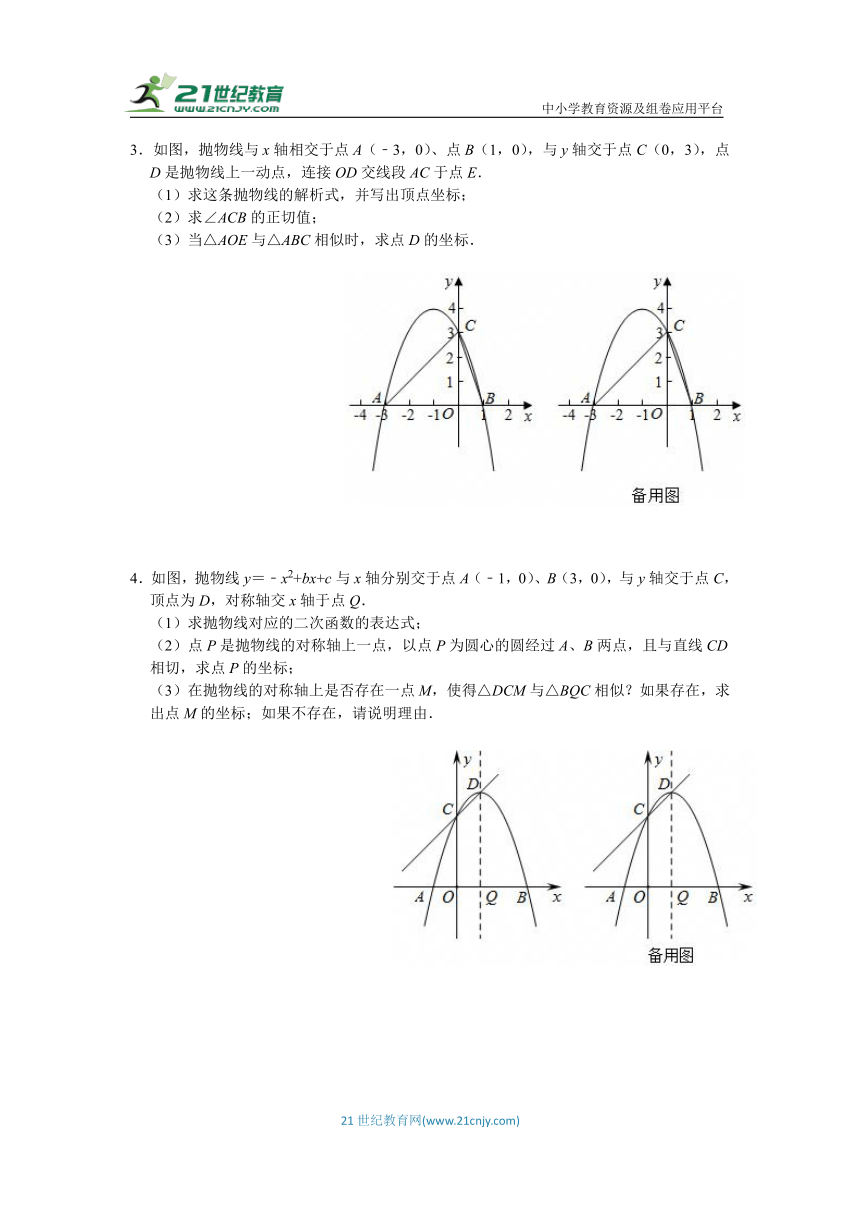
1.已知抛物线y=ax2﹣4x+3(a≠0)与x轴交于点A(1,0),B两点,与y轴交于点C.
(1)求抛物线解析式;
(2)若点P为抛物线上点,当PB=PC时,求点P坐标;
(3)若点M为线段BC上点(不含端点),且△MAB与△ABC相似,求点M坐标.
2.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
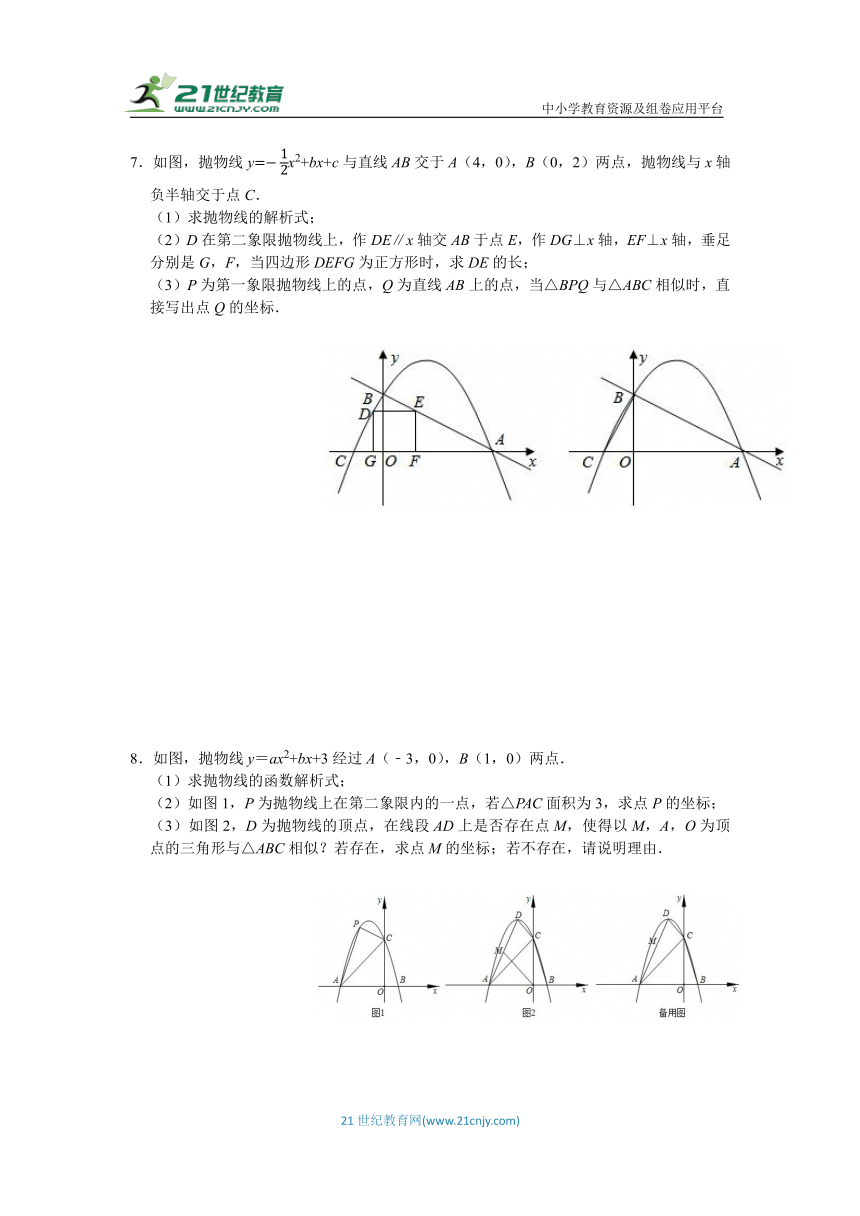
3.如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,连接OD交线段AC于点E.
(1)求这条抛物线的解析式,并写出顶点坐标;
(2)求∠ACB的正切值;
(3)当△AOE与△ABC相似时,求点D的坐标.
4.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.
5.如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
6.如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
7.如图,抛物线yx2+bx+c与直线AB交于A(4,0),B(0,2)两点,抛物线与x轴负半轴交于点C.
(1)求抛物线的解析式;
(2)D在第二象限抛物线上,作DE∥x轴交AB于点E,作DG⊥x轴,EF⊥x轴,垂足分别是G,F,当四边形DEFG为正方形时,求DE的长;
(3)P为第一象限抛物线上的点,Q为直线AB上的点,当△BPQ与△ABC相似时,直接写出点Q的坐标.
8.如图,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点.
(1)求抛物线的函数解析式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
9.二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0)
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
10.如图,已知抛物线y=ax2+bx+c与直线yx相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,),交x轴正半轴于点D,抛物线的顶点为M.
(1)求抛物线的表达式及点M的坐标;
(2)设P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求此时△PAB的面积及点P的坐标;
(3)Q为x轴上一动点,N是抛物线上一点,当△QMN∽△MAD(点Q与点M对应)时,求点Q的坐标.
11.如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.
(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
12.如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过原点和点A(4,0).经过点A的直线与该二次函数图象交于点B(1,3),与y轴交于点C.
(1)求二次函数的解析式及点C的坐标;
(2)点P是二次函数图象上的一个动点,当点P在直线AB上方时,过点P作PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为m.
①m为何值时线段PD的长度最大,并求出最大值;
②是否存在点P,使得△BPD与△AOC相似.若存在,请求出点P坐标;若不存在,请说明理由.
13.如图,抛物线y=﹣x2+bx+c上的点A,C坐标分别为(0,2),(4,0),抛物线与x轴负半轴交于点B,点M为y轴负半轴上一点,且OM=2,连接AC,CM.
(1)求点M的坐标及抛物线的解析式;
(2)点P是抛物线位于第一象限图象上的动点,连接AP,CP,当S△PAC=S△ACM时,求点P的坐标;
(3)点D是线段BC(包含点B,C)上的动点,过点D作x轴的垂线,交抛物线于点Q,交直线CM于点N,若以点Q,N,C为顶点的三角形与△COM相似,请直接写出点Q的坐标.
14.已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.
15.如图,在直角坐标系中,直线yx﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
(1)求抛物线的解析式;
(2)在线段AB上是否存在一点P,使以A,D,P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;如果不存在,请说明理由;
(3)若点Q在第三象限内,且tan∠AQD=2,线段CQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.
参考答案
1.【解答】解:(1)将点A的坐标代入抛物线表达式得:0=a﹣4+3,解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3…①,
令x=0,则y=3,令y=0,则x=1或3,
故点C(0,3)、点B(3,0);
(2)PB=PC时,则点P在线段BC的垂直平分线上,
线段BC的中点坐标为(,),
则BC中垂线的k值为1,过点(,),
则其表达式为:y=x…②,
①②联立并求解得:x,
则点P坐标为(,)或(,);
(3)M为线段BC上点(不含端点),且△MAB与△ABC相似,
则△MAB∽△ACB,即:,则MB,
过点M分别作x、y轴的垂线交于点H、G,
∵OB=OC=3,∴∠CBO=45°,
则MH=MG=MB,OH=OB﹣BH,
即点M(,)
2.【解答】解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入一次函数表达式得:3=4k+1,解得:k,
则一次函数表达式为:yx+1,则点A坐标为(﹣2,0),
把点C、B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a,
则二次函数表达式为:yx2x+1;
(2)①如图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB3,cos∠BAO,
则AQ,
则m2,
即:m的值为4或.
3.【解答】解:(1)设抛物线解析式为:y=ax2+bx+c,将点A(﹣3,0),B(1,0),C(0,3)分别代入得:
,
解得:,
故抛物线解析式为:y=﹣x2﹣2x+3.
由于y=﹣x2﹣2x+3=﹣(x+1)2+4,
所以该抛物线的顶点坐标是(﹣1,4);
(2)如图1,过点B作BH⊥AC于点H.
∵∠AOC=90°,OA=OC=3,
∴∠OAC=∠OCA=45°,AC=3.
∵∠BHA=90°,
∴∠HAB+∠HBA=90°.
∴∠HAB=∠HBA=45°.
∵在直角△AHB中,AH2+BH2=AB2,AB=4.
∴AH=BH=2.
∴CH=32.
∵∠BHC=90°,
∴tan∠ACB2;
(3)如图2,过点D作DK⊥x轴于点K,
设D(x,﹣x2﹣2x+3),则K(x,0).并由题意知点D位于第二象限.
∴DK=﹣x2﹣2x+3,OK=﹣x.
∵∠BAC是公共角,
∴当△AOE与△ABC相似时,有2种情况:
①∠AOD=∠ABC时,△AOE∽△ABC,
∴tan∠AOD=tan∠ABC=3.
∴3,解得x1,x2(舍去)
∴D(,).
②∠AOD=∠ACB时,△AOE∽△ACB,
∴tan∠AOD=tan∠ACB=2.
∴2,解得x1,x2(舍去)
∴D(,2).
综上所述,当△AOE与△ABC相似时,求点D的坐标是(,)或(,2).
4.【解答】解:(1)∵A(﹣1,0),B(3,0).
代入y=﹣x2+bx+c,得
,
解得 b=2,c=3.
∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;
(2)如图1,设直线CD切⊙P于点E.连接PE、PA,作CF⊥DQ于点F.
∴PE⊥CD,PE=PA.
由y=﹣x2+2x+3,得
对称轴为直线x=1,C(0,3)、D(1,4).
∴DF=4﹣3=1,CF=1,
∴DF=CF,
∴△DCF为等腰直角三角形.
∴∠CDF=45°,
∴∠EDP=∠EPD=45°,
∴DE=EP,
∴△DEP为等腰三角形.
设P(1,m),
∴EP2(4﹣m)2.
在△APQ中,∠PQA=90°,
∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2
∴(4﹣m)2=[1﹣(﹣1)]2+m2.
整理,得m2+8m﹣8=0
解得,m=﹣4±2.
∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).
(3)存在点M,使得△DCM∽△BQC.
如图2,连接CQ、CB、CM,
∵C(0,3),OB=3,∠COB=90°,
∴△COB为等腰直角三角形,
∴∠CBQ=45°,BC=3.
由(2)可知,∠CDM=45°,CD,
∴∠CBQ=∠CDM.
∴△DCM与△BQC相似有两种情况.
当时,
∴,解得DM.
∴QM=DQ﹣DM=4.
∴M1(1,).
当时,
∴,解得DM=3,
∴QM=DQ﹣DM=4﹣3=1.
∴M2(1,1).
综上,点M的坐标为或(1,1).
5.【解答】解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,
∴A(﹣4,0),B(0,4).
∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,
∴,
解得:b=﹣3,c=4,
∴抛物线的解析式为:y=﹣x2﹣3x+4.
(2)如图,连接AE、过点E作EF⊥y轴于点F,
设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),
则OC=﹣m,OF=﹣m2﹣3m+4,
∵OA=OB=4,
∴BF=﹣m2﹣3m,
则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF
(﹣m+4)(﹣m2﹣3m+4)4×4(﹣m)×(﹣m2﹣3m).
=﹣2m2﹣8m
=﹣2(m+2)2+8,
∵﹣4<m<0,
∴当m=﹣2时,S取得最大值,最大值为8.
即△ABE面积的最大值为8.
(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BDOCm,
则D(m,4+m).
∵△ACD为等腰直角三角形,△DBE和△DAC相似
∴△DBE必为等腰直角三角形.
i)若∠BED=90°,则BE=DE,
∵BE=OC=﹣m,
∴DE=BE=﹣m,
∴CE=4+m﹣m=4,
∴E(m,4).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,
∴D(﹣3,1);
ii)若∠EBD=90°,则BE=BDm,
在等腰直角三角形EBD中,DEBD=﹣2m,
∴CE=4+m﹣2m=4﹣m,
∴E(m,4﹣m).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,
∴D(﹣2,2).
综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).
6.【解答】解:(1)设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入得:3n=﹣3,解得n=﹣1.
∴抛物线的解析式为y=(x+3)(x﹣1)即y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4).
(2)如图1所示:过点E作ED⊥BC,垂足为D.
∵B(3,0),C(0,﹣3),
∴OC=OB=3.
∴∠OCB=∠OBC=45°,BC=3
∵点E与点C关于抛物线的对称轴对称,
∴CE⊥OC,
∴∠DCE=45°.
∵ED⊥CD,
∴△DEB为等腰直角三角形.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为x=1.
∴CE=2.
∴CD=ED.
∴BD=BC﹣CD=2.
∴tan∠CBE.
(3)如图2所示:
∵B(3,0),D(1,﹣4),
∴A(﹣1,0),F(1,0).
∴FB=2,DF=4.
∴tan∠FDB.
∴tan∠FDB=tan∠CBE.
∴∠FDB=∠CBE.
∴当时,△BCE∽△DBM.
∴,解得:MD.
∴点M的纵坐标=﹣4.
∴M(1,).
如图3所示:
∵∠FDB=∠CBE,
∴当∠BMD=∠BCE=45°时,△DMB∽△BCE.
∴FM=FB=2.
∴M(1,2).
综上所述,当点M的坐标为(1,)或(1,2)时,△DMB和△BCE相似.
7.【解答】解:(1)将点A(4,0),B(0,2)代入yx2+bx+c,
∴,
解得,
∴yx2x+2;
(2)设直线AB的解析式为y=kx+d,
∴,
∴,
∴yx+2,
设D(t,t2t+2),E(t2﹣3t,t2t+2),
∵DE∥x轴交AB于点E,
∴DE=t2﹣4t,
∵DG⊥x轴,
∴DGt2t+2,
∵四边形DEFG为正方形,
∴DG=DE,
∴t2﹣4tt2t+2,
解得t=4(舍)或t,
∴DE;
(3)令y=0,则x2x+2=0,
解得x=﹣1或x=4,
∴C(﹣1,0),
∵A(4,0),B(0,2),
∴AB=2,AC=5,BC,
∴△ABC是直角三角形,∠ABC=90°,
设P(m,m2m+2),Q(n,n+2),
①如图1,当∠BQP=90°,∠PBQ=∠CBA时,
过点P作PD⊥x轴交直线AB于点E,交x轴于点D,
∴E(m,m+2),
∴PEm2+2m,
∵∠PEQ=∠DEA,
∴∠QPE=∠BAC,
∵△ABC∽△PBQ,
∴∠PBQ=∠CBA,
∴∠PBQ=∠PEB,
∴PB=PE,
∴m2+(m2m)2=(m2+2m)2,
解得m,
∴P(,),
∴PE,
∵△ABC∽△PQB,
∴,
∴,
∴BQ,
∴,
∴n,
∴Q(,);
②如图2,当∠BQP=90°,∠PBQ=∠CAB时,
∴BP∥AC,
∴P点的纵坐标为2,
∴P(3,2),
∴BP=3,
∵△PBQ∽△CAB,
∴,即,
∴BQ,
∴,
∴n,
∴Q(,);
③如图3,当∠APB=90°,∠PBA=∠ACB时,
过点P作PD⊥x轴交AB于点E,
∴∠AED=∠ACB,
∵∠PEB=∠AED,
∴∠PEB=∠PBE,
∴PB=PE,
∵P(m,m2m+2),
∴E(m,m+2),
∴PEm2+2m,
∴m2+2m,
∴m,
∴P(,),
∴PB,
∵△ABC∽△QPB,
∴,即,
∴BQ,
∴,
∴n,
∴Q(,);
④如图4,当∠BPQ=90°,∠PBQ=∠CAB时,
∴BP∥AC,PQ∥y轴,
∴P点纵坐标为2,
∴P(3,2),Q(3,);
综上所述:Q点的坐标为(,)或(,)或(,)或(3,).
8.【解答】解:(1)把A(﹣3,0),B(1,0)代入抛物线解析式y=ax2+bx+3得,解得,
∴抛物线的函数表达式为y=﹣x2﹣2x+3;
(2)如解(2)图1,过P点作PQ平行y轴,交AC于Q点,
∵A(﹣3,0),C(0,3),
∴直线AC解析式为y=x+3,
设P点坐标为(x,﹣x2﹣2x+3.),则Q点坐标为(x,x+3),
∴PQ=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x.
∴S△PACPQ AO,
∴(﹣x2﹣3x)×3=3,
解得:x1=﹣1,x2=﹣2.
当x=﹣1时,P点坐标为(﹣1,4),
当x=﹣2时,P点坐标为(﹣2,3),
综上所述:若△PAC面积为3,点P的坐标为(﹣1,4)或(﹣2,3);
(3)存在,理由:
如解(3)图1,过D点作DF垂直x轴于F点,过A点作AE垂直BC于E点,
∵D为抛物线y=﹣x2﹣2x+3的顶点,
∴D点坐标为(﹣1,4),
又∵A(﹣3,0),
∴直线AD为y=2x+6,AF=2,DF=4,tan∠DAB=2,
∵B(1,0),C(0,3)
∴tan∠ABC=3,BC,sin∠ABC,
∴直线BC解析式为y=﹣3x+3.
∵AB=4,
∴AE=AB sin∠ABC=4,BE,
∴CE,
∴tan∠ACB,
∴tan∠ACB=tan∠DAB=2,
∴∠ACB=∠DAB,
∴使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,如解(3)图2,
Ⅰ.当∠AOM=∠CAB=45°时,△ABC∽△OMA,
即OM为y=﹣x,
设OM与AD的交点M(x,y)
依题意得:,解得,
即M点为(﹣2,2),
此时,MA:MO≠CA:AB,
故点M舍去;
Ⅱ.若∠AOM=∠CBA,即OM∥BC,
∵直线BC解析式为y=﹣3x+3.
∴直线OM为y=﹣3x,设直线OM与AD的交点M(x,y).则
依题意得:,解得,
即M点为(,),
此时,MA:MO=CA:AB,
故点M符合题设条件.
综上所述:存在使得以M,A,O为顶点的三角形与△ABC相似的点M,其坐标为(,).
9.【解答】解:(1)当x=0时,y=4,
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x﹣4),将点C的坐标代入得:﹣4a=4,解得a=﹣1,
∴抛物线的解析式为y=﹣x2+3x+4.
(2)x.
∴CD,EF.
设点N的坐标为(,a)则ND=4﹣a,NE=a.
当△CDN∽△FEN时,,即,解得a,
∴点N的坐标为(,).
当△CDN∽△NEF时,,即,解得:a=2.
∴点N的坐标为(,2).
综上所述,点N的坐标为(,)或(,2).
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连接EM交抛物线于点P.
∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,,
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,﹣2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:,解得k=﹣2,b=8,
∴直线EM的解析式为y=﹣2x+8.
将y=﹣2x+8与y=﹣x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=﹣2x+8得:y=0.
∴点P的坐标为(4,0).
10.【解答】解:(1)把点B(4,m)代入yx中,得m,
∴B(4,),
把点A(﹣1,0)、B(4,)、C(0,)代入抛物线中,得,
解得 ∴抛物线的解析式为yx2﹣x,
∵yx2﹣x(x﹣1)2﹣2,
∴点M的坐标为(1,﹣2).
(2)∵点P为直线AB下方抛物线上一动点,
∴﹣1<x<4,
如图1所示,过点P作y轴的平行线交AB于点H,
设点P的坐标为(m,m2﹣m),则点H(m,m),
S△PAB HP (xB﹣xA) (m2m+2)×5(m)2,
∵0,
∴当m时,S最大,最大为,此时点P(,).
(3)如图2所示,
令y=0,解得x1=﹣1,x2=3,
∴D(3,0),
∵M(1,﹣2),A(﹣1,0),
∴△AMD为等腰直角三角形,
设点N的坐标为(n,n2﹣n),
∵△QEN≌△MFQ(AAS),
∴FQ=EN=2,MF=EQn2﹣n,
∴n2﹣n1=n+2,
解得n=5或﹣1(舍),
∴点Q的坐标为(7,0),
根据对称性可知,点Q的坐标为(﹣5,0)时也满足条件,
∵△ADM是等腰直角三角形,
∴当点Q是AD的中点,N与A或D重合时,△QMN∽△MAD,
此时Q(1,0)时.
综上所述:点Q的坐标为(7,0)或(﹣5,0)或(1,0).
11.【解答】解:(1)抛物线解析式为y=a(x+1)(x﹣4),
即y=ax2﹣3ax﹣4a,
则﹣4a=2,解得a,
所以抛物线解析式为yx2x+2;
(2)①作PN⊥x轴于N,交BC于M,如图,
BC2,
当x=0时,yx2x+2=2,则C(0,2),
设直线BC的解析式为y=mx+n,
把C(0,2),B(4,0)得,解得,
∴直线BC的解析式为yx+2,
设P(t,t2t+2),则M(t,t+2),
∴PMt2t+2﹣(t+2)t2+2t,
∵∠NBM=∠NPQ,
∴△PQM∽△BOC,
∴,即PQ,
∴PQt2t(t﹣2)2,
∴当t=2时,线段PQ的最大值为;
②当∠PCQ=∠ABC时,△PCQ∽△ABC,
此时PC∥OB,点P和点C关于直线x对称,
∴此时P点坐标为(3,2);
当∠CPQ=∠OBC时,△CPQ∽△ABC,
∵∠OBC=∠NPQ,
∴∠CPQ=∠MPQ,
而PQ⊥CM,
∴△PCM为等腰三角形,
∴PC=PM,
∴t2+(t2t+2﹣2)2=(t2+2t)2,
解得t,
此时P点坐标为(,),
综上所述,满足条件的P点坐标为(3,2)或(,).
12.【解答】解:(1)∵抛二次函数经过O(0,0),A(4,0),B(1,3),
∴将三点坐标代入解析式得,
解得:a=﹣1,b=4,c=0,
∴二次函数的解析式为:y=﹣x2+4x;
∵直线经过A、B两点,设直线AB解析式为:y=kx+n,
∴将A、B两点代入得,
解得:k=﹣1,n=4,
∴直线AB解析式为:y=﹣x+4,
∵点C是直线与y轴交点,
∴令x=0,则y=4,
∴C(0,4).
(2)①∵点P在直线AB上方,
∴0≤m≤4,
由题知P(m,﹣m2+4m),D(m,﹣m+4),
∴PD=yP﹣yD=﹣m2+4m+m﹣4=﹣m2+5m﹣4=﹣(m)2,
∵﹣1<0
∴当m时,PD是最大值.
②存在,理由如下:
∵∠PDB=∠ADE,∠ADE=∠ACO,
∴∠BDP=∠ACO,
∵△AOC是直角三角形,
∴要使△BPD与△AOC相似,只有保证△BPD是直角三角形就可以.
(Ⅰ)当△BPD∽△AOC时,
∵∠AOC=90°,
∴∠BPD=90°,
此时BP∥x轴,B、P关于对称轴对称,
∴P(3,3);
(Ⅱ)法一:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
∵OC=OA=4,
∴∠BDP=∠ADE=∠OAC=45°,
∴△BDP为等腰直角三角形,
∴PDBD,
由①知PD=﹣m2+5m﹣4,
∵B(1,3),D(m,﹣m+4),
∴BD(m﹣1),
∵PDBD,
∴﹣m2+5m﹣4=2(m﹣1),
解得m1=2,m2=1(舍),
∴P(2,4).
法二:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
过B作GH∥y轴,作PG⊥GH,作DH⊥GH,
则易证△PGB∽△BHD,
∴,
∵PG=m﹣1,BG=﹣m2+4m﹣3,BH=m﹣1,DH=m﹣1,
∴,
解得m1=2,m2=1(舍),
∴P(2,4).
法三:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
∴AB⊥PB,
∵kAC=﹣1,
∴kBP=1,
∴直线BP的解析式为:y=x+2,
联立方程组得,
解得:或,
∴P(2,4)
综上,存在点P使△BPD与△AOC相似,此时P的坐标为(3,3)或(2,4).
13.【解答】解:(1)∵点M在y轴负半轴且OM=2,
∴M(0,﹣2),
将A(0,2),C(4,0)代入y=﹣x2+bx+c,得,
解得,
∴抛物线的解析式为;
(2)过点P作PF⊥x轴于点F,交线段AC于点E,
设直线AC的解析式为y=kx+m(k≠0),
将A(0,2),C(4,0)代入y=kx+m,得,
解得,
∴直线AC的解析式为,
设点P的横坐标为p(0<p<4),
则,,
∴,
∵S△ACM=8,
∴,
解得p1=p2=2,
∴P(2,5);
(3),,
∵在△COM中,∠COM=90°,以点Q,N,C为顶点的三角形与△COM相似,
∴以点Q,N,C为顶点的三角形也是直角三角形,
又∵QD⊥x轴,直线QD交直线CM于点N,
∴∠CNQ≠90°,即点N不与点O是对应点.
故分为∠CQN=90°和∠QCN=90°两种情况讨论:
①当∠CQN=90°时,由于QN⊥x轴,
∴CQ⊥y轴,即CQ在x轴上,
又∵点Q在抛物线上,
∴此时点B与点Q重合,
作出图形如下:
此时∠CQN=∠COM=90°,
又∵∠QCN=∠OCM
∴△CQN∽△COM,即此时符合题意,
令,
解得:(舍去)
∴点Q的坐标,也即点B的坐标是.
②当∠QCN=90°时,作图如下:
∵QD⊥x轴,∠COM=90°
∴QD∥OM,
∴∠CNQ=∠OMC,
∵∠CNQ=∠OMC,∠QCN=∠COM=90°,
∴△QCN∽△COM,即此时符合题意,
∵△QCN∽△COM,
∴∠CQN=∠OCM,即∠DQC=∠OCM
∵∠DQC=∠OCM,∠QDC=∠COM,
∴△QDC∽△COM,
∴,QD=2DC,
设点Q的横坐标为q,则,D(q,0),
∴,CD=4﹣q,
∴,
解得:(舍去),
∴,
∴点Q的坐标是,
综上所述:点Q的坐标是,.
14.【解答】解:(1)设二次函数的解析式为y=a(x﹣1)2﹣2,
∵A(3,0)在抛物线上,
∴0=a(3﹣1)2﹣2
∴a,
∴y(x﹣1)2﹣2,
(2)抛物线与y轴交点B的坐标为(0,),
设直线AB的解析式为y=kx+m,
∴,
∴,
∴直线AB的解析式为yx.
∵P为线段AB上的一个动点,
∴P点坐标为(x,x).(0<x<3)
由题意可知PE∥y轴,∴E点坐标为(x,x2﹣x),
∵0<x<3,
∴PE=(x)﹣(x2﹣x)x2x,
(3)由题意可知D点横坐标为x=1,又D点在直线AB上,
∴D点坐标(1,﹣1).
①当∠EDP=90°时,△AOB∽△EDP,
∴.
过点D作DQ⊥PE于Q,
∴xQ=xP=x,yQ=﹣1,
∴△DQP∽△AOB∽△EDP,
∴,
又OA=3,OB,AB,
又DQ=x﹣1,
∴DP(x﹣1),
∴,
解得:x=﹣1±(负值舍去).
∴P(1,)(如图中的P1点);
②当∠DEP=90°时,△AOB∽△DEP,
∴.
由(2)PEx2x,DE=x﹣1,
∴,
解得:x=1±,(负值舍去).
∴P(1,1)(如图中的P2点);
综上所述,P点坐标为(1,)或(1,1).
15.【解答】解:(1)由已知,点A坐标为(﹣3,0)
∵直线x=﹣1为对称轴
∴点C坐标为(1,0)
∴抛物线解析式为:y=(x+3)(x﹣1)=x2+2x﹣3
(2)存在
由已知点D坐标为(﹣1,0)
设点P的横坐标为(a,a﹣1)
当△AOB∽△ADP时
∴a=﹣1
点P坐标为(﹣1,)
当△AOB∽△APD时
过点P作PE⊥x轴于点E
则△APE∽△APDE
∴PE2=AE ED
∴(a﹣1)2=(a+3)(﹣a﹣1)
解得a1=﹣3(舍去),a2
∴点P坐标为(,)
(3)存在,CQ最小值为
如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,)为圆心.
∵tan∠AFD=2
∴(A、D除外)上的点都是满足条件的Q点.
连CE交⊙E于点Q,则CQ为满足条件的最小值
此时CE,⊙E半径为
∴CQ最小值为
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习二次函数中相似三角形存在性问题练习
1.已知抛物线y=ax2﹣4x+3(a≠0)与x轴交于点A(1,0),B两点,与y轴交于点C.
(1)求抛物线解析式;
(2)若点P为抛物线上点,当PB=PC时,求点P坐标;
(3)若点M为线段BC上点(不含端点),且△MAB与△ABC相似,求点M坐标.
2.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
3.如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,连接OD交线段AC于点E.
(1)求这条抛物线的解析式,并写出顶点坐标;
(2)求∠ACB的正切值;
(3)当△AOE与△ABC相似时,求点D的坐标.
4.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.
5.如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
6.如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
7.如图,抛物线yx2+bx+c与直线AB交于A(4,0),B(0,2)两点,抛物线与x轴负半轴交于点C.
(1)求抛物线的解析式;
(2)D在第二象限抛物线上,作DE∥x轴交AB于点E,作DG⊥x轴,EF⊥x轴,垂足分别是G,F,当四边形DEFG为正方形时,求DE的长;
(3)P为第一象限抛物线上的点,Q为直线AB上的点,当△BPQ与△ABC相似时,直接写出点Q的坐标.
8.如图,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点.
(1)求抛物线的函数解析式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
9.二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0)
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
10.如图,已知抛物线y=ax2+bx+c与直线yx相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,),交x轴正半轴于点D,抛物线的顶点为M.
(1)求抛物线的表达式及点M的坐标;
(2)设P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求此时△PAB的面积及点P的坐标;
(3)Q为x轴上一动点,N是抛物线上一点,当△QMN∽△MAD(点Q与点M对应)时,求点Q的坐标.
11.如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.
(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
12.如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过原点和点A(4,0).经过点A的直线与该二次函数图象交于点B(1,3),与y轴交于点C.
(1)求二次函数的解析式及点C的坐标;
(2)点P是二次函数图象上的一个动点,当点P在直线AB上方时,过点P作PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为m.
①m为何值时线段PD的长度最大,并求出最大值;
②是否存在点P,使得△BPD与△AOC相似.若存在,请求出点P坐标;若不存在,请说明理由.
13.如图,抛物线y=﹣x2+bx+c上的点A,C坐标分别为(0,2),(4,0),抛物线与x轴负半轴交于点B,点M为y轴负半轴上一点,且OM=2,连接AC,CM.
(1)求点M的坐标及抛物线的解析式;
(2)点P是抛物线位于第一象限图象上的动点,连接AP,CP,当S△PAC=S△ACM时,求点P的坐标;
(3)点D是线段BC(包含点B,C)上的动点,过点D作x轴的垂线,交抛物线于点Q,交直线CM于点N,若以点Q,N,C为顶点的三角形与△COM相似,请直接写出点Q的坐标.
14.已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.
15.如图,在直角坐标系中,直线yx﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
(1)求抛物线的解析式;
(2)在线段AB上是否存在一点P,使以A,D,P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;如果不存在,请说明理由;
(3)若点Q在第三象限内,且tan∠AQD=2,线段CQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.
参考答案
1.【解答】解:(1)将点A的坐标代入抛物线表达式得:0=a﹣4+3,解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3…①,
令x=0,则y=3,令y=0,则x=1或3,
故点C(0,3)、点B(3,0);
(2)PB=PC时,则点P在线段BC的垂直平分线上,
线段BC的中点坐标为(,),
则BC中垂线的k值为1,过点(,),
则其表达式为:y=x…②,
①②联立并求解得:x,
则点P坐标为(,)或(,);
(3)M为线段BC上点(不含端点),且△MAB与△ABC相似,
则△MAB∽△ACB,即:,则MB,
过点M分别作x、y轴的垂线交于点H、G,
∵OB=OC=3,∴∠CBO=45°,
则MH=MG=MB,OH=OB﹣BH,
即点M(,)
2.【解答】解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入一次函数表达式得:3=4k+1,解得:k,
则一次函数表达式为:yx+1,则点A坐标为(﹣2,0),
把点C、B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a,
则二次函数表达式为:yx2x+1;
(2)①如图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB3,cos∠BAO,
则AQ,
则m2,
即:m的值为4或.
3.【解答】解:(1)设抛物线解析式为:y=ax2+bx+c,将点A(﹣3,0),B(1,0),C(0,3)分别代入得:
,
解得:,
故抛物线解析式为:y=﹣x2﹣2x+3.
由于y=﹣x2﹣2x+3=﹣(x+1)2+4,
所以该抛物线的顶点坐标是(﹣1,4);
(2)如图1,过点B作BH⊥AC于点H.
∵∠AOC=90°,OA=OC=3,
∴∠OAC=∠OCA=45°,AC=3.
∵∠BHA=90°,
∴∠HAB+∠HBA=90°.
∴∠HAB=∠HBA=45°.
∵在直角△AHB中,AH2+BH2=AB2,AB=4.
∴AH=BH=2.
∴CH=32.
∵∠BHC=90°,
∴tan∠ACB2;
(3)如图2,过点D作DK⊥x轴于点K,
设D(x,﹣x2﹣2x+3),则K(x,0).并由题意知点D位于第二象限.
∴DK=﹣x2﹣2x+3,OK=﹣x.
∵∠BAC是公共角,
∴当△AOE与△ABC相似时,有2种情况:
①∠AOD=∠ABC时,△AOE∽△ABC,
∴tan∠AOD=tan∠ABC=3.
∴3,解得x1,x2(舍去)
∴D(,).
②∠AOD=∠ACB时,△AOE∽△ACB,
∴tan∠AOD=tan∠ACB=2.
∴2,解得x1,x2(舍去)
∴D(,2).
综上所述,当△AOE与△ABC相似时,求点D的坐标是(,)或(,2).
4.【解答】解:(1)∵A(﹣1,0),B(3,0).
代入y=﹣x2+bx+c,得
,
解得 b=2,c=3.
∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;
(2)如图1,设直线CD切⊙P于点E.连接PE、PA,作CF⊥DQ于点F.
∴PE⊥CD,PE=PA.
由y=﹣x2+2x+3,得
对称轴为直线x=1,C(0,3)、D(1,4).
∴DF=4﹣3=1,CF=1,
∴DF=CF,
∴△DCF为等腰直角三角形.
∴∠CDF=45°,
∴∠EDP=∠EPD=45°,
∴DE=EP,
∴△DEP为等腰三角形.
设P(1,m),
∴EP2(4﹣m)2.
在△APQ中,∠PQA=90°,
∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2
∴(4﹣m)2=[1﹣(﹣1)]2+m2.
整理,得m2+8m﹣8=0
解得,m=﹣4±2.
∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).
(3)存在点M,使得△DCM∽△BQC.
如图2,连接CQ、CB、CM,
∵C(0,3),OB=3,∠COB=90°,
∴△COB为等腰直角三角形,
∴∠CBQ=45°,BC=3.
由(2)可知,∠CDM=45°,CD,
∴∠CBQ=∠CDM.
∴△DCM与△BQC相似有两种情况.
当时,
∴,解得DM.
∴QM=DQ﹣DM=4.
∴M1(1,).
当时,
∴,解得DM=3,
∴QM=DQ﹣DM=4﹣3=1.
∴M2(1,1).
综上,点M的坐标为或(1,1).
5.【解答】解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,
∴A(﹣4,0),B(0,4).
∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,
∴,
解得:b=﹣3,c=4,
∴抛物线的解析式为:y=﹣x2﹣3x+4.
(2)如图,连接AE、过点E作EF⊥y轴于点F,
设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),
则OC=﹣m,OF=﹣m2﹣3m+4,
∵OA=OB=4,
∴BF=﹣m2﹣3m,
则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF
(﹣m+4)(﹣m2﹣3m+4)4×4(﹣m)×(﹣m2﹣3m).
=﹣2m2﹣8m
=﹣2(m+2)2+8,
∵﹣4<m<0,
∴当m=﹣2时,S取得最大值,最大值为8.
即△ABE面积的最大值为8.
(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BDOCm,
则D(m,4+m).
∵△ACD为等腰直角三角形,△DBE和△DAC相似
∴△DBE必为等腰直角三角形.
i)若∠BED=90°,则BE=DE,
∵BE=OC=﹣m,
∴DE=BE=﹣m,
∴CE=4+m﹣m=4,
∴E(m,4).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,
∴D(﹣3,1);
ii)若∠EBD=90°,则BE=BDm,
在等腰直角三角形EBD中,DEBD=﹣2m,
∴CE=4+m﹣2m=4﹣m,
∴E(m,4﹣m).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,
∴D(﹣2,2).
综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).
6.【解答】解:(1)设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入得:3n=﹣3,解得n=﹣1.
∴抛物线的解析式为y=(x+3)(x﹣1)即y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4).
(2)如图1所示:过点E作ED⊥BC,垂足为D.
∵B(3,0),C(0,﹣3),
∴OC=OB=3.
∴∠OCB=∠OBC=45°,BC=3
∵点E与点C关于抛物线的对称轴对称,
∴CE⊥OC,
∴∠DCE=45°.
∵ED⊥CD,
∴△DEB为等腰直角三角形.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为x=1.
∴CE=2.
∴CD=ED.
∴BD=BC﹣CD=2.
∴tan∠CBE.
(3)如图2所示:
∵B(3,0),D(1,﹣4),
∴A(﹣1,0),F(1,0).
∴FB=2,DF=4.
∴tan∠FDB.
∴tan∠FDB=tan∠CBE.
∴∠FDB=∠CBE.
∴当时,△BCE∽△DBM.
∴,解得:MD.
∴点M的纵坐标=﹣4.
∴M(1,).
如图3所示:
∵∠FDB=∠CBE,
∴当∠BMD=∠BCE=45°时,△DMB∽△BCE.
∴FM=FB=2.
∴M(1,2).
综上所述,当点M的坐标为(1,)或(1,2)时,△DMB和△BCE相似.
7.【解答】解:(1)将点A(4,0),B(0,2)代入yx2+bx+c,
∴,
解得,
∴yx2x+2;
(2)设直线AB的解析式为y=kx+d,
∴,
∴,
∴yx+2,
设D(t,t2t+2),E(t2﹣3t,t2t+2),
∵DE∥x轴交AB于点E,
∴DE=t2﹣4t,
∵DG⊥x轴,
∴DGt2t+2,
∵四边形DEFG为正方形,
∴DG=DE,
∴t2﹣4tt2t+2,
解得t=4(舍)或t,
∴DE;
(3)令y=0,则x2x+2=0,
解得x=﹣1或x=4,
∴C(﹣1,0),
∵A(4,0),B(0,2),
∴AB=2,AC=5,BC,
∴△ABC是直角三角形,∠ABC=90°,
设P(m,m2m+2),Q(n,n+2),
①如图1,当∠BQP=90°,∠PBQ=∠CBA时,
过点P作PD⊥x轴交直线AB于点E,交x轴于点D,
∴E(m,m+2),
∴PEm2+2m,
∵∠PEQ=∠DEA,
∴∠QPE=∠BAC,
∵△ABC∽△PBQ,
∴∠PBQ=∠CBA,
∴∠PBQ=∠PEB,
∴PB=PE,
∴m2+(m2m)2=(m2+2m)2,
解得m,
∴P(,),
∴PE,
∵△ABC∽△PQB,
∴,
∴,
∴BQ,
∴,
∴n,
∴Q(,);
②如图2,当∠BQP=90°,∠PBQ=∠CAB时,
∴BP∥AC,
∴P点的纵坐标为2,
∴P(3,2),
∴BP=3,
∵△PBQ∽△CAB,
∴,即,
∴BQ,
∴,
∴n,
∴Q(,);
③如图3,当∠APB=90°,∠PBA=∠ACB时,
过点P作PD⊥x轴交AB于点E,
∴∠AED=∠ACB,
∵∠PEB=∠AED,
∴∠PEB=∠PBE,
∴PB=PE,
∵P(m,m2m+2),
∴E(m,m+2),
∴PEm2+2m,
∴m2+2m,
∴m,
∴P(,),
∴PB,
∵△ABC∽△QPB,
∴,即,
∴BQ,
∴,
∴n,
∴Q(,);
④如图4,当∠BPQ=90°,∠PBQ=∠CAB时,
∴BP∥AC,PQ∥y轴,
∴P点纵坐标为2,
∴P(3,2),Q(3,);
综上所述:Q点的坐标为(,)或(,)或(,)或(3,).
8.【解答】解:(1)把A(﹣3,0),B(1,0)代入抛物线解析式y=ax2+bx+3得,解得,
∴抛物线的函数表达式为y=﹣x2﹣2x+3;
(2)如解(2)图1,过P点作PQ平行y轴,交AC于Q点,
∵A(﹣3,0),C(0,3),
∴直线AC解析式为y=x+3,
设P点坐标为(x,﹣x2﹣2x+3.),则Q点坐标为(x,x+3),
∴PQ=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x.
∴S△PACPQ AO,
∴(﹣x2﹣3x)×3=3,
解得:x1=﹣1,x2=﹣2.
当x=﹣1时,P点坐标为(﹣1,4),
当x=﹣2时,P点坐标为(﹣2,3),
综上所述:若△PAC面积为3,点P的坐标为(﹣1,4)或(﹣2,3);
(3)存在,理由:
如解(3)图1,过D点作DF垂直x轴于F点,过A点作AE垂直BC于E点,
∵D为抛物线y=﹣x2﹣2x+3的顶点,
∴D点坐标为(﹣1,4),
又∵A(﹣3,0),
∴直线AD为y=2x+6,AF=2,DF=4,tan∠DAB=2,
∵B(1,0),C(0,3)
∴tan∠ABC=3,BC,sin∠ABC,
∴直线BC解析式为y=﹣3x+3.
∵AB=4,
∴AE=AB sin∠ABC=4,BE,
∴CE,
∴tan∠ACB,
∴tan∠ACB=tan∠DAB=2,
∴∠ACB=∠DAB,
∴使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,如解(3)图2,
Ⅰ.当∠AOM=∠CAB=45°时,△ABC∽△OMA,
即OM为y=﹣x,
设OM与AD的交点M(x,y)
依题意得:,解得,
即M点为(﹣2,2),
此时,MA:MO≠CA:AB,
故点M舍去;
Ⅱ.若∠AOM=∠CBA,即OM∥BC,
∵直线BC解析式为y=﹣3x+3.
∴直线OM为y=﹣3x,设直线OM与AD的交点M(x,y).则
依题意得:,解得,
即M点为(,),
此时,MA:MO=CA:AB,
故点M符合题设条件.
综上所述:存在使得以M,A,O为顶点的三角形与△ABC相似的点M,其坐标为(,).
9.【解答】解:(1)当x=0时,y=4,
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x﹣4),将点C的坐标代入得:﹣4a=4,解得a=﹣1,
∴抛物线的解析式为y=﹣x2+3x+4.
(2)x.
∴CD,EF.
设点N的坐标为(,a)则ND=4﹣a,NE=a.
当△CDN∽△FEN时,,即,解得a,
∴点N的坐标为(,).
当△CDN∽△NEF时,,即,解得:a=2.
∴点N的坐标为(,2).
综上所述,点N的坐标为(,)或(,2).
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连接EM交抛物线于点P.
∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,,
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,﹣2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:,解得k=﹣2,b=8,
∴直线EM的解析式为y=﹣2x+8.
将y=﹣2x+8与y=﹣x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=﹣2x+8得:y=0.
∴点P的坐标为(4,0).
10.【解答】解:(1)把点B(4,m)代入yx中,得m,
∴B(4,),
把点A(﹣1,0)、B(4,)、C(0,)代入抛物线中,得,
解得 ∴抛物线的解析式为yx2﹣x,
∵yx2﹣x(x﹣1)2﹣2,
∴点M的坐标为(1,﹣2).
(2)∵点P为直线AB下方抛物线上一动点,
∴﹣1<x<4,
如图1所示,过点P作y轴的平行线交AB于点H,
设点P的坐标为(m,m2﹣m),则点H(m,m),
S△PAB HP (xB﹣xA) (m2m+2)×5(m)2,
∵0,
∴当m时,S最大,最大为,此时点P(,).
(3)如图2所示,
令y=0,解得x1=﹣1,x2=3,
∴D(3,0),
∵M(1,﹣2),A(﹣1,0),
∴△AMD为等腰直角三角形,
设点N的坐标为(n,n2﹣n),
∵△QEN≌△MFQ(AAS),
∴FQ=EN=2,MF=EQn2﹣n,
∴n2﹣n1=n+2,
解得n=5或﹣1(舍),
∴点Q的坐标为(7,0),
根据对称性可知,点Q的坐标为(﹣5,0)时也满足条件,
∵△ADM是等腰直角三角形,
∴当点Q是AD的中点,N与A或D重合时,△QMN∽△MAD,
此时Q(1,0)时.
综上所述:点Q的坐标为(7,0)或(﹣5,0)或(1,0).
11.【解答】解:(1)抛物线解析式为y=a(x+1)(x﹣4),
即y=ax2﹣3ax﹣4a,
则﹣4a=2,解得a,
所以抛物线解析式为yx2x+2;
(2)①作PN⊥x轴于N,交BC于M,如图,
BC2,
当x=0时,yx2x+2=2,则C(0,2),
设直线BC的解析式为y=mx+n,
把C(0,2),B(4,0)得,解得,
∴直线BC的解析式为yx+2,
设P(t,t2t+2),则M(t,t+2),
∴PMt2t+2﹣(t+2)t2+2t,
∵∠NBM=∠NPQ,
∴△PQM∽△BOC,
∴,即PQ,
∴PQt2t(t﹣2)2,
∴当t=2时,线段PQ的最大值为;
②当∠PCQ=∠ABC时,△PCQ∽△ABC,
此时PC∥OB,点P和点C关于直线x对称,
∴此时P点坐标为(3,2);
当∠CPQ=∠OBC时,△CPQ∽△ABC,
∵∠OBC=∠NPQ,
∴∠CPQ=∠MPQ,
而PQ⊥CM,
∴△PCM为等腰三角形,
∴PC=PM,
∴t2+(t2t+2﹣2)2=(t2+2t)2,
解得t,
此时P点坐标为(,),
综上所述,满足条件的P点坐标为(3,2)或(,).
12.【解答】解:(1)∵抛二次函数经过O(0,0),A(4,0),B(1,3),
∴将三点坐标代入解析式得,
解得:a=﹣1,b=4,c=0,
∴二次函数的解析式为:y=﹣x2+4x;
∵直线经过A、B两点,设直线AB解析式为:y=kx+n,
∴将A、B两点代入得,
解得:k=﹣1,n=4,
∴直线AB解析式为:y=﹣x+4,
∵点C是直线与y轴交点,
∴令x=0,则y=4,
∴C(0,4).
(2)①∵点P在直线AB上方,
∴0≤m≤4,
由题知P(m,﹣m2+4m),D(m,﹣m+4),
∴PD=yP﹣yD=﹣m2+4m+m﹣4=﹣m2+5m﹣4=﹣(m)2,
∵﹣1<0
∴当m时,PD是最大值.
②存在,理由如下:
∵∠PDB=∠ADE,∠ADE=∠ACO,
∴∠BDP=∠ACO,
∵△AOC是直角三角形,
∴要使△BPD与△AOC相似,只有保证△BPD是直角三角形就可以.
(Ⅰ)当△BPD∽△AOC时,
∵∠AOC=90°,
∴∠BPD=90°,
此时BP∥x轴,B、P关于对称轴对称,
∴P(3,3);
(Ⅱ)法一:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
∵OC=OA=4,
∴∠BDP=∠ADE=∠OAC=45°,
∴△BDP为等腰直角三角形,
∴PDBD,
由①知PD=﹣m2+5m﹣4,
∵B(1,3),D(m,﹣m+4),
∴BD(m﹣1),
∵PDBD,
∴﹣m2+5m﹣4=2(m﹣1),
解得m1=2,m2=1(舍),
∴P(2,4).
法二:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
过B作GH∥y轴,作PG⊥GH,作DH⊥GH,
则易证△PGB∽△BHD,
∴,
∵PG=m﹣1,BG=﹣m2+4m﹣3,BH=m﹣1,DH=m﹣1,
∴,
解得m1=2,m2=1(舍),
∴P(2,4).
法三:当△PBD∽△AOC时,
∴∠PBD=∠AOC=90°,
∴AB⊥PB,
∵kAC=﹣1,
∴kBP=1,
∴直线BP的解析式为:y=x+2,
联立方程组得,
解得:或,
∴P(2,4)
综上,存在点P使△BPD与△AOC相似,此时P的坐标为(3,3)或(2,4).
13.【解答】解:(1)∵点M在y轴负半轴且OM=2,
∴M(0,﹣2),
将A(0,2),C(4,0)代入y=﹣x2+bx+c,得,
解得,
∴抛物线的解析式为;
(2)过点P作PF⊥x轴于点F,交线段AC于点E,
设直线AC的解析式为y=kx+m(k≠0),
将A(0,2),C(4,0)代入y=kx+m,得,
解得,
∴直线AC的解析式为,
设点P的横坐标为p(0<p<4),
则,,
∴,
∵S△ACM=8,
∴,
解得p1=p2=2,
∴P(2,5);
(3),,
∵在△COM中,∠COM=90°,以点Q,N,C为顶点的三角形与△COM相似,
∴以点Q,N,C为顶点的三角形也是直角三角形,
又∵QD⊥x轴,直线QD交直线CM于点N,
∴∠CNQ≠90°,即点N不与点O是对应点.
故分为∠CQN=90°和∠QCN=90°两种情况讨论:
①当∠CQN=90°时,由于QN⊥x轴,
∴CQ⊥y轴,即CQ在x轴上,
又∵点Q在抛物线上,
∴此时点B与点Q重合,
作出图形如下:
此时∠CQN=∠COM=90°,
又∵∠QCN=∠OCM
∴△CQN∽△COM,即此时符合题意,
令,
解得:(舍去)
∴点Q的坐标,也即点B的坐标是.
②当∠QCN=90°时,作图如下:
∵QD⊥x轴,∠COM=90°
∴QD∥OM,
∴∠CNQ=∠OMC,
∵∠CNQ=∠OMC,∠QCN=∠COM=90°,
∴△QCN∽△COM,即此时符合题意,
∵△QCN∽△COM,
∴∠CQN=∠OCM,即∠DQC=∠OCM
∵∠DQC=∠OCM,∠QDC=∠COM,
∴△QDC∽△COM,
∴,QD=2DC,
设点Q的横坐标为q,则,D(q,0),
∴,CD=4﹣q,
∴,
解得:(舍去),
∴,
∴点Q的坐标是,
综上所述:点Q的坐标是,.
14.【解答】解:(1)设二次函数的解析式为y=a(x﹣1)2﹣2,
∵A(3,0)在抛物线上,
∴0=a(3﹣1)2﹣2
∴a,
∴y(x﹣1)2﹣2,
(2)抛物线与y轴交点B的坐标为(0,),
设直线AB的解析式为y=kx+m,
∴,
∴,
∴直线AB的解析式为yx.
∵P为线段AB上的一个动点,
∴P点坐标为(x,x).(0<x<3)
由题意可知PE∥y轴,∴E点坐标为(x,x2﹣x),
∵0<x<3,
∴PE=(x)﹣(x2﹣x)x2x,
(3)由题意可知D点横坐标为x=1,又D点在直线AB上,
∴D点坐标(1,﹣1).
①当∠EDP=90°时,△AOB∽△EDP,
∴.
过点D作DQ⊥PE于Q,
∴xQ=xP=x,yQ=﹣1,
∴△DQP∽△AOB∽△EDP,
∴,
又OA=3,OB,AB,
又DQ=x﹣1,
∴DP(x﹣1),
∴,
解得:x=﹣1±(负值舍去).
∴P(1,)(如图中的P1点);
②当∠DEP=90°时,△AOB∽△DEP,
∴.
由(2)PEx2x,DE=x﹣1,
∴,
解得:x=1±,(负值舍去).
∴P(1,1)(如图中的P2点);
综上所述,P点坐标为(1,)或(1,1).
15.【解答】解:(1)由已知,点A坐标为(﹣3,0)
∵直线x=﹣1为对称轴
∴点C坐标为(1,0)
∴抛物线解析式为:y=(x+3)(x﹣1)=x2+2x﹣3
(2)存在
由已知点D坐标为(﹣1,0)
设点P的横坐标为(a,a﹣1)
当△AOB∽△ADP时
∴a=﹣1
点P坐标为(﹣1,)
当△AOB∽△APD时
过点P作PE⊥x轴于点E
则△APE∽△APDE
∴PE2=AE ED
∴(a﹣1)2=(a+3)(﹣a﹣1)
解得a1=﹣3(舍去),a2
∴点P坐标为(,)
(3)存在,CQ最小值为
如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,)为圆心.
∵tan∠AFD=2
∴(A、D除外)上的点都是满足条件的Q点.
连CE交⊙E于点Q,则CQ为满足条件的最小值
此时CE,⊙E半径为
∴CQ最小值为
21世纪教育网(www.21cnjy.com)
同课章节目录
