2025年九年级中考数学三轮冲刺练习二次函数应用综合练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习二次函数应用综合练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:07:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习二次函数应用综合练习
1.某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数解析式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?
2.某超市以每件10元的价格购进一种文具,销售时该文具的销售单价不低于进价且不高于19元.经过市场调查发现,该文具的每天销售数量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如下表所示:
销售单价x/元 … 12 13 14 …
每天销售数量y/件 … 36 34 32 …
(1)直接写出y与x之间的函数关系式;
(2)若该超市每天销售这种文具获利192元,则销售单价为多少元?
(3)设销售这种文具每天获利w(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
3.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药.学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
4.某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
5.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(50≤x≤65),y表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
6.某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高x元.
(1)服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?
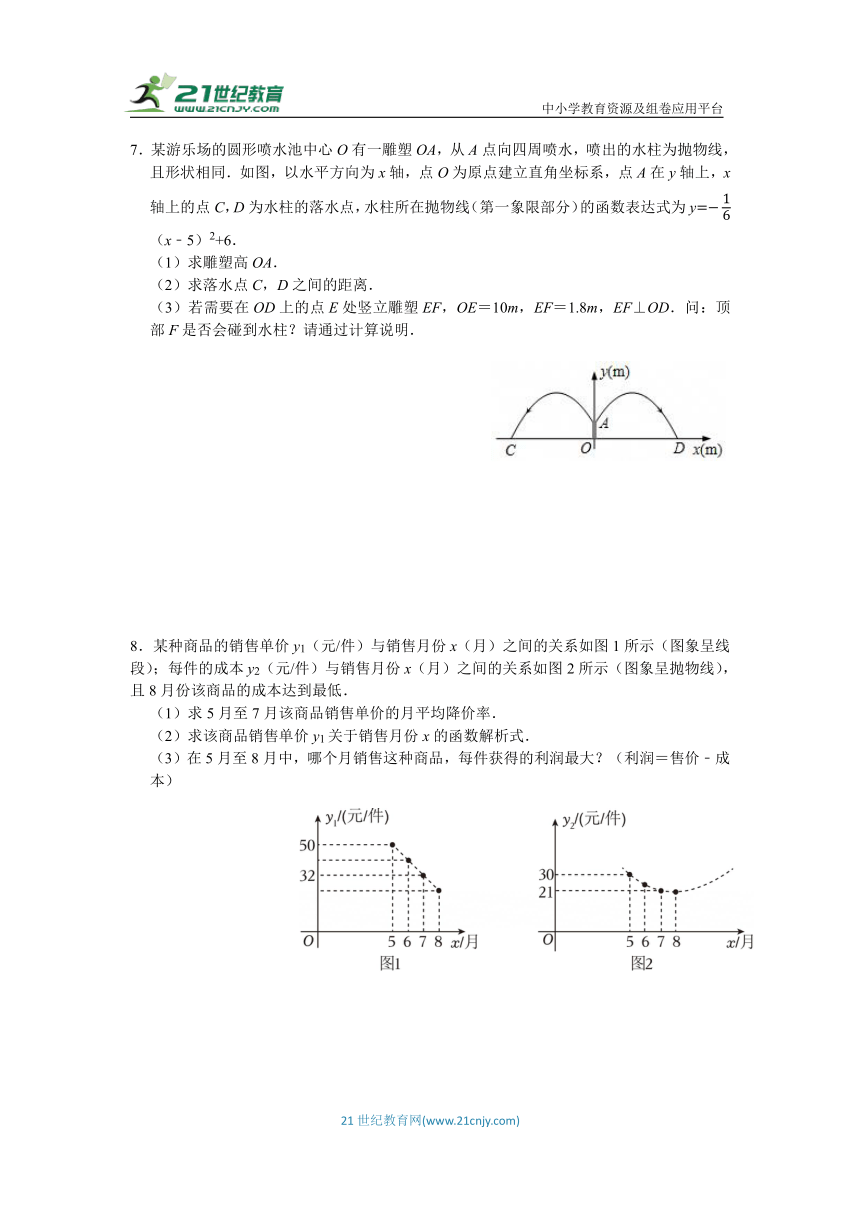
7.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
8.某种商品的销售单价y1(元/件)与销售月份x(月)之间的关系如图1所示(图象呈线段);每件的成本y2(元/件)与销售月份x(月)之间的关系如图2所示(图象呈抛物线),且8月份该商品的成本达到最低.
(1)求5月至7月该商品销售单价的月平均降价率.
(2)求该商品销售单价y1关于销售月份x的函数解析式.
(3)在5月至8月中,哪个月销售这种商品,每件获得的利润最大?(利润=售价﹣成本)
9.某超市在春节前夕,购进一批大米,每袋进价30元,超市规定每袋售价不得少于40元.根据以往销售经验发现:当售价为每袋40元时,每天可以卖出500袋,每袋售价每提高1元,每天要少卖出20袋.
(1)试求出每天的销售量y袋与每袋售价x元之间的函数关系式;
(2)当每袋售价定为多少元时,每天销售的利润T元最大?最大利润是多少?
(3)如果这种大米的每袋售价不高于46元,超市想要每天获得不低于6000元的利润,那么超市每天至少销售大米多少袋?
10.某公司生产一种建筑材料,生产费用y(万元)由材料费用、人工费用和制造费用三部分组成,已知该公司每年的材料费用(万元)与生产吨数x(吨)成正比,制造费用(万元)与生产吨数(吨)的平方成正比,人工费用为固定费用1000万元,试行中得到了下表中的数据.
生产吨数(吨) 50 70
生产费用(万元) 1500 1840
(1)求y与x的函数解析式;
(2)已知卖出x吨该建筑材料的单价为P万元/吨,其中(a为常数).设出售x吨时的利润为w万元.
①求w与x的函数解析式;
②如果生产出来的产品全部卖掉,并且当生产吨数是150吨时,所获利润最大,求此时P的值.
11.某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克4元的大米,以不低于成本价且不超过每千克7元的价格销售,当每千克售价为5元时,每天售出大米950千克,市场调查反应,每千克大米价格每上涨1元,每天要少卖出50千克大米.
(1)写出超市销售这种大米,每天所得的销售利润w(元)与每千克售价x(元)之间的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到1800元?
(3)当每千克售价定为多少元时,每天获得利润最大?最大利润为多少?
12.近来网络上流传着“不是羽绒服买不起,是军大衣更有性价比”的说法.察觉到商机的某服装超市以每件80元的价格购进一批军大衣,商家经过调查统计,当每件军大衣售价为130元时,一天可以卖出100件,在此基础上,售价每降1元,则每天的销售量会增加10件.
设每件商品的售价为x(x≥80)元,每天可获得的销售利润为y元.
(1)用含x的代数式表示下列各量:
①每件军大衣的利润为 元;
②每天军大衣的销售量为 件.
(2)每件商品的售价定为多少元时,每天可获得的销售利润最大,最大利润是多少?
13.2025年第九届亚洲冬季运动会在哈尔滨举办.“冰雪同梦,亚洲同心”推动亚洲各国携手合作,共同发展.亚冬会吉祥物“滨滨”和“妮妮”寓意“哈尔滨欢迎您”.亚运会特许商品零售店预售吉祥物“滨滨”,该吉祥物每个进价为30元,规定售价不低于进价.现在售价为每个50元,每天可销售100个.经市场调查发现,若售价每降价1元,则每天的销售量将增加10个.设每个吉祥物降价x元(x为整数),每天的销售量为y元,
(1)直接写出y与x之间的函数关系式;
(2)设每天销售吉祥物“滨滨”的利润为W元,求出W与x的函数关系式;
(3)在(2)的条件下,特许零售店如何定价,才能使每天销售吉祥物“滨滨”的利润W最大?最大利润是多少元?
14.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线yx+b.其中,当火箭运行的水平距离为9km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15km.
15.一座三拱桥横跨于湖面之上,三个桥洞L1,L2,L3均呈抛物线型且抛物线形状相同,如图所示,以AB中点O为坐标原点,AB所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.
已知:桥洞L1的最大高度OC为8米,跨度AB=32米,桥洞L2,L3关于y轴对称,且最大高度均为4米.
(1)求桥洞L1所在抛物线的函数表达式;
(2)如图所示,现需要在桥洞L2,L3上安装两盏靠近y轴的照明灯Q,P,且照明灯的高度都是2米,请计算照明灯的水平距离PQ的长度.
参考答案
1.【解答】解:(1)由题意,设一次函数的解析式为y=kx+b,
又过(100,300),(120,200),
∴.
∴.
∴所求函数解析式为y=﹣5x+800.
(2)由题意得,,
∴100≤x≤116.
∵商场获得的利润=(x﹣80)(﹣5x+800)
=﹣5x2+1200x﹣64000
=﹣5(x﹣120)2+8000,
又﹣5<0,100≤x≤116,
∴当x=116时,利润最大,最大值为7920.
答:当销售单价为116时,商场获得利润最大,最大利润是7920元.
2.【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由所给函表格可知:
,
解得:,
故y与x的函数关系式为y=﹣2x+60;
(2)根据题意得:
(x﹣10)(﹣2x+60)=192,
解得:x1=18,x2=22
又∵10≤x≤19,
∴x=18,
答:销售单价应为18元.
(3)w=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600=﹣2(x﹣20)2+200
∵a=﹣2<0,
∴抛物线开口向下,
∵对称轴为直线 x=20,
∴当10≤x≤19时,w随x的增大而增大,
∴当 x=19 时,w有最大值,w最大=198.
答:当销售单价为19元时,每天获利最大,最大利润是198元.
3.【解答】解:(1)设垂直于墙的边为x米,围成的矩形面积为S平方米,则平行于墙的边为(120﹣3x)米,
根据题意得:S=x(120﹣3x)=﹣3x2+120x=﹣3(x﹣20)2+1200,
∵﹣3<0,
∴当x=20时,S取最大值1200,
∴120﹣3x=120﹣3×20=60,
∴垂直于墙的边为20米,平行于墙的边为60米,花园面积最大为1200平方米;
(2)设购买牡丹m株,则购买芍药1200×2﹣m=(2400﹣m)株,
∵学校计划购买费用不超过5万元,
∴25m+15(2400﹣m)≤50000,
解得m≤1400,
∴最多可以购买1400株牡丹.
4.【解答】解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为:y=kx+b,
由题意可知:,
解得:,
∴y与x之间的函数关系式为:y=﹣5x+150;
(2)(﹣5x+150)(x﹣8)=425,
解得:x1=13,x2=25(舍去),
∴若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为13元;
(3)w=y(x﹣8),
=(﹣5x+150)(x﹣8),
w=﹣5x2+190x﹣1200,
=﹣5(x﹣19)2+605,
∵8≤x≤15,且x为整数,
当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为525.
答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
5.【解答】解:(1)设猪肉粽每盒进价a元,则豆沙粽每盒进价(a﹣10)元,
则,
解得:a=40,经检验a=40是方程的解,
∴猪肉粽每盒进价40元,豆沙粽每盒进价30元,
(2)由题意得,当x=50时,每天可售出100盒,
当猪肉粽每盒售价x元(50≤x≤65)时,每天可售[100﹣2(x﹣50)]盒,
∴y=x[100﹣2(x﹣50)]﹣40×[100﹣2(x﹣50)]=﹣2x2+280x﹣8000,
配方,得:y=﹣2(x﹣70)2+1800,
∵x<70时,y随x的增大而增大,
∴当x=65时,y取最大值,最大值为:﹣2×(65﹣70)2+1800=1750(元).
答:y关于x的函数解析式为y=﹣2x2+280x﹣8000(50≤x≤65),且最大利润为1750元.
6.【解答】解:(1)设T恤的销售单价提高x元,
由题意列方程得:(x+40﹣30)(300﹣10x)=3360,
解得:x1=2或x2=18,
∵要尽可能减少库存,
∴x2=18不合题意,应舍去.
∴T恤的销售单价应提高2元,
答:T恤的销售单价应提高2元;
(2)设利润为M元,由题意可得:
M=(x+40﹣30)(300﹣10x),
=﹣10x2+200x+3000,
=﹣10(x﹣10)2+4000,
∴当x=10时,M最大值 =4000元,
∴销售单价:40+10=50(元),
答:当服装店将销售单价定为50元时,得到最大利润是4000元.
7.【解答】解:(1)当x=0时,y(0﹣5)2+6,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y(10﹣5)2+6,
∴点(10,)在抛物线y(x﹣5)2+6上.
又∵1.83>1.8,
∴顶部F不会碰到水柱.
8.【解答】解:(1)设5月至7月该商品销售单价的月平均降价率为x,
根据题意得:50(1﹣x)2=32,
解得x1=0.2,x2=1.8(不符合题意,舍去),
答:5月至7月该商品销售单价的月平均降价率为20%;
(2)设y1关于x的函数解析式为y1=kx+b,
把点(5,50)与点(7,32)代入y1=kx+b中得:
,
解得:,
∴y1关于x的函数解析式为:y1=﹣9x+95;
(3)∵抛物线的顶点坐标是(8,21),
∴设y2关于x的函数解析式为.
把点(5,30)代入中得:
a(5﹣8)2+21=30,
解得:a=1,
∴,
设销售这种商品每件获得的利润是w元.
则,
∵a=﹣1,b=7,
∴,
∴该抛物线开口向下,对称轴直线是,
∴在对称轴的右侧,y随x的增大而减小.
∵x=5,6,7,8,
∴当x=5时,w取最大值,
∴5月销售这种商品,每件获得的利润最大.
9.【解答】解(1)当每袋售价x元时,则y=500﹣(x﹣40)×20=﹣20x+1300,
500÷20+40=25+40=65(元)
即y=﹣20x+1300(40≤x≤65);
(2)依题意可得:
,
当x=47.5时,T有最大利润为6125元;
(3)由题意可得:40≤x≤46,且T=﹣20x2+1900x﹣39000≥6000,
解得45≤x≤50,
∴45≤x≤46,
∵y=﹣20x+1300中的y随x的增大而减小,
∴当x=46时,y=﹣20×46+1300=380,
即ymin=380.
答:超市每天至少销售大米380袋.
10.【解答】解:(1)依题意,设材料费用为y1=k1x,制造费用为,
则:,
根据题意可知,(50,1500),(70,1840)满足解析式,
代入可得:,
解得:,
∴y与x的函数解析式为:y=0.1x2+5x+1000;
(2)①w=P x﹣y
,
综上所述,w与x的函数解析式为:;
②∵,
配方得:,
∵当生产吨数是150吨时,利润最大,
即当x=150时,w有最大值,
∴,
解得a=45,此时P=4540.
11.【解答】解:(1)根据题意得每天售出大米的数量可得:w=(x﹣4)(1200﹣50x)=﹣50x2+1400x﹣4800,
由条件可知4≤x≤7,
∴每天所得的销售利润w(元)与每千克售价x(元)之间的函数关系式为w=﹣50x2+1400x﹣4800(4≤x≤7);
(2)当每天销售该大米的利润达到1800元时,
依题意得:﹣50x2+1400x﹣4800=1800,
解得:x1=22(舍去),x2=6,
∴超市将该大米每千克售价定为6元时,每天销售该大米的利润可达到1800元;
(3)由(1)知:w=﹣50x2+1400x﹣4800(4≤x≤7),
∴w=﹣50(x﹣14)2+5000,
∵﹣50<0,对称轴为x=14,
∴当x<14时,y随x的增大而增大,
又∵4≤x≤7,
∴当x=7时,(元),
∴当每千克售价定为7元时,每天获利最大,最大利润为2550元.
12.【解答】解:(1)①∵每件商品的售价为x(x≥80)元,每件军大衣的进价为80元,
∴每件军大衣的利润为(x﹣80)元;
②由条件可知:每天军大衣的销售量为100﹣10(x﹣130)=(1400﹣10x)件,
故答案为:①(x﹣80);②(1400﹣10x);
(2)根据题意得:y=(x﹣80)(1400﹣10x)=﹣10x2+2200x﹣112000=﹣10(x﹣110)2+9000
∵﹣10<0,
∴当x=110时,y取最大值,最大值为9000,
答:每件商品的售价定为110元时,每天可获得的销售利润最大,最大利润是9000元.
13.【解答】解:(1)由题意,∵售价为每个50元,每天可销售100个.售价每降价1元,每天的销售量将增加10个.设每个吉祥物降价x元(x为整数),每天的销售量为y个,
∴y与x之间的函数关系式为y=100+10x;
(2)由题意,结合(1),∵y=100+10x,
∴W与x的函数关系式为W=(50﹣30﹣x)y=(20﹣x)(100+10x)=﹣10(x﹣5)2+2250(0<x≤20);
(3)由题意,∵W=﹣10(x﹣5)2+2250,﹣10<0,
∴当x=5时,w有最大值,且最大值为2250,此时定价为:50﹣5=45(元).
14.【解答】解:(1)①∵y=ax2+x经过点(9,3.6),
∴81a+9=3.6.
解得:a.
∵yx+b经过点(9,3.6),
∴3.69+b.
解得:b=8.1;
②由①得:yx2+x
(x2﹣15x)
(x)2(0≤x≤9).
∴火箭运行的最高点是km.
∴1.35=2.4(km).
∴2.4x2+x.
整理得:x2﹣15x+36=0.
解得:x1=12>9(不合题意,舍去),x2=3.
由①得:yx+8.1.
∴2.4x+8.1.
解得:x=11.4.
∴11.4﹣3=8.4(km).
答:这两个位置之间的距离为8.4km;
(2)当x=9时,y=81a+9.
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15km.
∴yx+b经过点(9,81a+9),(15,0)
∴.
解得:.
∴a<0时,火箭落地点与发射点的水平距离超过15km.
15.【解答】解:(1)由题意得,顶点C(0,8),
∴可设桥洞L1所在抛物线的函数表达式为y=ax2+8.
∵AB=32,
∴B(16,0).
∴256a+8=0.
∴a.
∴桥洞L1所在抛物线的函数表达式yx2+8.
(2)由题意,∵桥洞L1所在抛物线的函数表达式yx2+8,且三个桥洞L1,L2,L3均呈抛物线型且抛物线形状相同,
∴可设桥洞L2所在抛物线的函数表达式y(x﹣h)2+k,桥洞L3所在抛物线的函数表达式y(x+h)2+k(h>16).
又∵桥洞L2,L3关于y轴对称,且最大高度均为4米,
∴k=4.
∴桥洞L2所在抛物线的函数表达式y(x﹣h)2+4,桥洞L3所在抛物线的函数表达式y(x+h)2+4.
又∵A(﹣16,0),B(16,0),
∴(16﹣h)2+4=0.
∴h=16+8或h=16﹣8(舍去).
∴桥洞L2所在抛物线的函数表达式y(x﹣16﹣8)2+4,桥洞L3所在抛物线的函数表达式y(x+16+8)2+4.
令y=2,
∴x=8+8或24+8(舍去);x=﹣8﹣8或﹣24﹣8(舍去).
∴PQ=8+8(﹣8﹣8)=(16+16)(米).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习二次函数应用综合练习
1.某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数解析式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?
2.某超市以每件10元的价格购进一种文具,销售时该文具的销售单价不低于进价且不高于19元.经过市场调查发现,该文具的每天销售数量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如下表所示:
销售单价x/元 … 12 13 14 …
每天销售数量y/件 … 36 34 32 …
(1)直接写出y与x之间的函数关系式;
(2)若该超市每天销售这种文具获利192元,则销售单价为多少元?
(3)设销售这种文具每天获利w(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
3.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药.学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
4.某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
5.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(50≤x≤65),y表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
6.某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高x元.
(1)服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?
7.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
8.某种商品的销售单价y1(元/件)与销售月份x(月)之间的关系如图1所示(图象呈线段);每件的成本y2(元/件)与销售月份x(月)之间的关系如图2所示(图象呈抛物线),且8月份该商品的成本达到最低.
(1)求5月至7月该商品销售单价的月平均降价率.
(2)求该商品销售单价y1关于销售月份x的函数解析式.
(3)在5月至8月中,哪个月销售这种商品,每件获得的利润最大?(利润=售价﹣成本)
9.某超市在春节前夕,购进一批大米,每袋进价30元,超市规定每袋售价不得少于40元.根据以往销售经验发现:当售价为每袋40元时,每天可以卖出500袋,每袋售价每提高1元,每天要少卖出20袋.
(1)试求出每天的销售量y袋与每袋售价x元之间的函数关系式;
(2)当每袋售价定为多少元时,每天销售的利润T元最大?最大利润是多少?
(3)如果这种大米的每袋售价不高于46元,超市想要每天获得不低于6000元的利润,那么超市每天至少销售大米多少袋?
10.某公司生产一种建筑材料,生产费用y(万元)由材料费用、人工费用和制造费用三部分组成,已知该公司每年的材料费用(万元)与生产吨数x(吨)成正比,制造费用(万元)与生产吨数(吨)的平方成正比,人工费用为固定费用1000万元,试行中得到了下表中的数据.
生产吨数(吨) 50 70
生产费用(万元) 1500 1840
(1)求y与x的函数解析式;
(2)已知卖出x吨该建筑材料的单价为P万元/吨,其中(a为常数).设出售x吨时的利润为w万元.
①求w与x的函数解析式;
②如果生产出来的产品全部卖掉,并且当生产吨数是150吨时,所获利润最大,求此时P的值.
11.某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克4元的大米,以不低于成本价且不超过每千克7元的价格销售,当每千克售价为5元时,每天售出大米950千克,市场调查反应,每千克大米价格每上涨1元,每天要少卖出50千克大米.
(1)写出超市销售这种大米,每天所得的销售利润w(元)与每千克售价x(元)之间的函数关系式;
(2)超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到1800元?
(3)当每千克售价定为多少元时,每天获得利润最大?最大利润为多少?
12.近来网络上流传着“不是羽绒服买不起,是军大衣更有性价比”的说法.察觉到商机的某服装超市以每件80元的价格购进一批军大衣,商家经过调查统计,当每件军大衣售价为130元时,一天可以卖出100件,在此基础上,售价每降1元,则每天的销售量会增加10件.
设每件商品的售价为x(x≥80)元,每天可获得的销售利润为y元.
(1)用含x的代数式表示下列各量:
①每件军大衣的利润为 元;
②每天军大衣的销售量为 件.
(2)每件商品的售价定为多少元时,每天可获得的销售利润最大,最大利润是多少?
13.2025年第九届亚洲冬季运动会在哈尔滨举办.“冰雪同梦,亚洲同心”推动亚洲各国携手合作,共同发展.亚冬会吉祥物“滨滨”和“妮妮”寓意“哈尔滨欢迎您”.亚运会特许商品零售店预售吉祥物“滨滨”,该吉祥物每个进价为30元,规定售价不低于进价.现在售价为每个50元,每天可销售100个.经市场调查发现,若售价每降价1元,则每天的销售量将增加10个.设每个吉祥物降价x元(x为整数),每天的销售量为y元,
(1)直接写出y与x之间的函数关系式;
(2)设每天销售吉祥物“滨滨”的利润为W元,求出W与x的函数关系式;
(3)在(2)的条件下,特许零售店如何定价,才能使每天销售吉祥物“滨滨”的利润W最大?最大利润是多少元?
14.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线yx+b.其中,当火箭运行的水平距离为9km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15km.
15.一座三拱桥横跨于湖面之上,三个桥洞L1,L2,L3均呈抛物线型且抛物线形状相同,如图所示,以AB中点O为坐标原点,AB所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.
已知:桥洞L1的最大高度OC为8米,跨度AB=32米,桥洞L2,L3关于y轴对称,且最大高度均为4米.
(1)求桥洞L1所在抛物线的函数表达式;
(2)如图所示,现需要在桥洞L2,L3上安装两盏靠近y轴的照明灯Q,P,且照明灯的高度都是2米,请计算照明灯的水平距离PQ的长度.
参考答案
1.【解答】解:(1)由题意,设一次函数的解析式为y=kx+b,
又过(100,300),(120,200),
∴.
∴.
∴所求函数解析式为y=﹣5x+800.
(2)由题意得,,
∴100≤x≤116.
∵商场获得的利润=(x﹣80)(﹣5x+800)
=﹣5x2+1200x﹣64000
=﹣5(x﹣120)2+8000,
又﹣5<0,100≤x≤116,
∴当x=116时,利润最大,最大值为7920.
答:当销售单价为116时,商场获得利润最大,最大利润是7920元.
2.【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由所给函表格可知:
,
解得:,
故y与x的函数关系式为y=﹣2x+60;
(2)根据题意得:
(x﹣10)(﹣2x+60)=192,
解得:x1=18,x2=22
又∵10≤x≤19,
∴x=18,
答:销售单价应为18元.
(3)w=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600=﹣2(x﹣20)2+200
∵a=﹣2<0,
∴抛物线开口向下,
∵对称轴为直线 x=20,
∴当10≤x≤19时,w随x的增大而增大,
∴当 x=19 时,w有最大值,w最大=198.
答:当销售单价为19元时,每天获利最大,最大利润是198元.
3.【解答】解:(1)设垂直于墙的边为x米,围成的矩形面积为S平方米,则平行于墙的边为(120﹣3x)米,
根据题意得:S=x(120﹣3x)=﹣3x2+120x=﹣3(x﹣20)2+1200,
∵﹣3<0,
∴当x=20时,S取最大值1200,
∴120﹣3x=120﹣3×20=60,
∴垂直于墙的边为20米,平行于墙的边为60米,花园面积最大为1200平方米;
(2)设购买牡丹m株,则购买芍药1200×2﹣m=(2400﹣m)株,
∵学校计划购买费用不超过5万元,
∴25m+15(2400﹣m)≤50000,
解得m≤1400,
∴最多可以购买1400株牡丹.
4.【解答】解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为:y=kx+b,
由题意可知:,
解得:,
∴y与x之间的函数关系式为:y=﹣5x+150;
(2)(﹣5x+150)(x﹣8)=425,
解得:x1=13,x2=25(舍去),
∴若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为13元;
(3)w=y(x﹣8),
=(﹣5x+150)(x﹣8),
w=﹣5x2+190x﹣1200,
=﹣5(x﹣19)2+605,
∵8≤x≤15,且x为整数,
当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为525.
答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
5.【解答】解:(1)设猪肉粽每盒进价a元,则豆沙粽每盒进价(a﹣10)元,
则,
解得:a=40,经检验a=40是方程的解,
∴猪肉粽每盒进价40元,豆沙粽每盒进价30元,
(2)由题意得,当x=50时,每天可售出100盒,
当猪肉粽每盒售价x元(50≤x≤65)时,每天可售[100﹣2(x﹣50)]盒,
∴y=x[100﹣2(x﹣50)]﹣40×[100﹣2(x﹣50)]=﹣2x2+280x﹣8000,
配方,得:y=﹣2(x﹣70)2+1800,
∵x<70时,y随x的增大而增大,
∴当x=65时,y取最大值,最大值为:﹣2×(65﹣70)2+1800=1750(元).
答:y关于x的函数解析式为y=﹣2x2+280x﹣8000(50≤x≤65),且最大利润为1750元.
6.【解答】解:(1)设T恤的销售单价提高x元,
由题意列方程得:(x+40﹣30)(300﹣10x)=3360,
解得:x1=2或x2=18,
∵要尽可能减少库存,
∴x2=18不合题意,应舍去.
∴T恤的销售单价应提高2元,
答:T恤的销售单价应提高2元;
(2)设利润为M元,由题意可得:
M=(x+40﹣30)(300﹣10x),
=﹣10x2+200x+3000,
=﹣10(x﹣10)2+4000,
∴当x=10时,M最大值 =4000元,
∴销售单价:40+10=50(元),
答:当服装店将销售单价定为50元时,得到最大利润是4000元.
7.【解答】解:(1)当x=0时,y(0﹣5)2+6,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y(10﹣5)2+6,
∴点(10,)在抛物线y(x﹣5)2+6上.
又∵1.83>1.8,
∴顶部F不会碰到水柱.
8.【解答】解:(1)设5月至7月该商品销售单价的月平均降价率为x,
根据题意得:50(1﹣x)2=32,
解得x1=0.2,x2=1.8(不符合题意,舍去),
答:5月至7月该商品销售单价的月平均降价率为20%;
(2)设y1关于x的函数解析式为y1=kx+b,
把点(5,50)与点(7,32)代入y1=kx+b中得:
,
解得:,
∴y1关于x的函数解析式为:y1=﹣9x+95;
(3)∵抛物线的顶点坐标是(8,21),
∴设y2关于x的函数解析式为.
把点(5,30)代入中得:
a(5﹣8)2+21=30,
解得:a=1,
∴,
设销售这种商品每件获得的利润是w元.
则,
∵a=﹣1,b=7,
∴,
∴该抛物线开口向下,对称轴直线是,
∴在对称轴的右侧,y随x的增大而减小.
∵x=5,6,7,8,
∴当x=5时,w取最大值,
∴5月销售这种商品,每件获得的利润最大.
9.【解答】解(1)当每袋售价x元时,则y=500﹣(x﹣40)×20=﹣20x+1300,
500÷20+40=25+40=65(元)
即y=﹣20x+1300(40≤x≤65);
(2)依题意可得:
,
当x=47.5时,T有最大利润为6125元;
(3)由题意可得:40≤x≤46,且T=﹣20x2+1900x﹣39000≥6000,
解得45≤x≤50,
∴45≤x≤46,
∵y=﹣20x+1300中的y随x的增大而减小,
∴当x=46时,y=﹣20×46+1300=380,
即ymin=380.
答:超市每天至少销售大米380袋.
10.【解答】解:(1)依题意,设材料费用为y1=k1x,制造费用为,
则:,
根据题意可知,(50,1500),(70,1840)满足解析式,
代入可得:,
解得:,
∴y与x的函数解析式为:y=0.1x2+5x+1000;
(2)①w=P x﹣y
,
综上所述,w与x的函数解析式为:;
②∵,
配方得:,
∵当生产吨数是150吨时,利润最大,
即当x=150时,w有最大值,
∴,
解得a=45,此时P=4540.
11.【解答】解:(1)根据题意得每天售出大米的数量可得:w=(x﹣4)(1200﹣50x)=﹣50x2+1400x﹣4800,
由条件可知4≤x≤7,
∴每天所得的销售利润w(元)与每千克售价x(元)之间的函数关系式为w=﹣50x2+1400x﹣4800(4≤x≤7);
(2)当每天销售该大米的利润达到1800元时,
依题意得:﹣50x2+1400x﹣4800=1800,
解得:x1=22(舍去),x2=6,
∴超市将该大米每千克售价定为6元时,每天销售该大米的利润可达到1800元;
(3)由(1)知:w=﹣50x2+1400x﹣4800(4≤x≤7),
∴w=﹣50(x﹣14)2+5000,
∵﹣50<0,对称轴为x=14,
∴当x<14时,y随x的增大而增大,
又∵4≤x≤7,
∴当x=7时,(元),
∴当每千克售价定为7元时,每天获利最大,最大利润为2550元.
12.【解答】解:(1)①∵每件商品的售价为x(x≥80)元,每件军大衣的进价为80元,
∴每件军大衣的利润为(x﹣80)元;
②由条件可知:每天军大衣的销售量为100﹣10(x﹣130)=(1400﹣10x)件,
故答案为:①(x﹣80);②(1400﹣10x);
(2)根据题意得:y=(x﹣80)(1400﹣10x)=﹣10x2+2200x﹣112000=﹣10(x﹣110)2+9000
∵﹣10<0,
∴当x=110时,y取最大值,最大值为9000,
答:每件商品的售价定为110元时,每天可获得的销售利润最大,最大利润是9000元.
13.【解答】解:(1)由题意,∵售价为每个50元,每天可销售100个.售价每降价1元,每天的销售量将增加10个.设每个吉祥物降价x元(x为整数),每天的销售量为y个,
∴y与x之间的函数关系式为y=100+10x;
(2)由题意,结合(1),∵y=100+10x,
∴W与x的函数关系式为W=(50﹣30﹣x)y=(20﹣x)(100+10x)=﹣10(x﹣5)2+2250(0<x≤20);
(3)由题意,∵W=﹣10(x﹣5)2+2250,﹣10<0,
∴当x=5时,w有最大值,且最大值为2250,此时定价为:50﹣5=45(元).
14.【解答】解:(1)①∵y=ax2+x经过点(9,3.6),
∴81a+9=3.6.
解得:a.
∵yx+b经过点(9,3.6),
∴3.69+b.
解得:b=8.1;
②由①得:yx2+x
(x2﹣15x)
(x)2(0≤x≤9).
∴火箭运行的最高点是km.
∴1.35=2.4(km).
∴2.4x2+x.
整理得:x2﹣15x+36=0.
解得:x1=12>9(不合题意,舍去),x2=3.
由①得:yx+8.1.
∴2.4x+8.1.
解得:x=11.4.
∴11.4﹣3=8.4(km).
答:这两个位置之间的距离为8.4km;
(2)当x=9时,y=81a+9.
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15km.
∴yx+b经过点(9,81a+9),(15,0)
∴.
解得:.
∴a<0时,火箭落地点与发射点的水平距离超过15km.
15.【解答】解:(1)由题意得,顶点C(0,8),
∴可设桥洞L1所在抛物线的函数表达式为y=ax2+8.
∵AB=32,
∴B(16,0).
∴256a+8=0.
∴a.
∴桥洞L1所在抛物线的函数表达式yx2+8.
(2)由题意,∵桥洞L1所在抛物线的函数表达式yx2+8,且三个桥洞L1,L2,L3均呈抛物线型且抛物线形状相同,
∴可设桥洞L2所在抛物线的函数表达式y(x﹣h)2+k,桥洞L3所在抛物线的函数表达式y(x+h)2+k(h>16).
又∵桥洞L2,L3关于y轴对称,且最大高度均为4米,
∴k=4.
∴桥洞L2所在抛物线的函数表达式y(x﹣h)2+4,桥洞L3所在抛物线的函数表达式y(x+h)2+4.
又∵A(﹣16,0),B(16,0),
∴(16﹣h)2+4=0.
∴h=16+8或h=16﹣8(舍去).
∴桥洞L2所在抛物线的函数表达式y(x﹣16﹣8)2+4,桥洞L3所在抛物线的函数表达式y(x+16+8)2+4.
令y=2,
∴x=8+8或24+8(舍去);x=﹣8﹣8或﹣24﹣8(舍去).
∴PQ=8+8(﹣8﹣8)=(16+16)(米).
21世纪教育网(www.21cnjy.com)
同课章节目录
