2025年九年级中考数学三轮冲刺图形的旋转的综合练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺图形的旋转的综合练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:05:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺图形的旋转的综合练习
一、选择题
1.如图,将△ABC绕点A逆时针旋转α°得到△AB'C'.当点B,C,B'在同一直线上,∠BAC=100°,α=150时,∠C'=( )
A.60° B.65° C.70° D.75°
2.如图,在△AOB中,∠AOB=90°,OA=OB=6.将△AOB绕点O顺时针旋转45°,得到△A'OB',A'B'与OB相交于点D,则OD的长为( )
A.2 B.3 C.2 D.3
3.如图,将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,若CD=3,BC=1,则AD的长为( )
A. B. C.2 D.
4.如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD,将线段DC绕点D顺时针旋转30°得到线段DF,点E为AB的中点,连接EF,ED.若EF=1,则△BED的面积是( )
A. B. C. D.
5.如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
6.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
7.如图,等边△ABC的边长为2,点D在AB上,BD,连接CD,将CD绕点C按顺时针方向旋转60°得到CE,连接DE交AC于点G.则点G到CD的距离为( )
A. B. C. D.
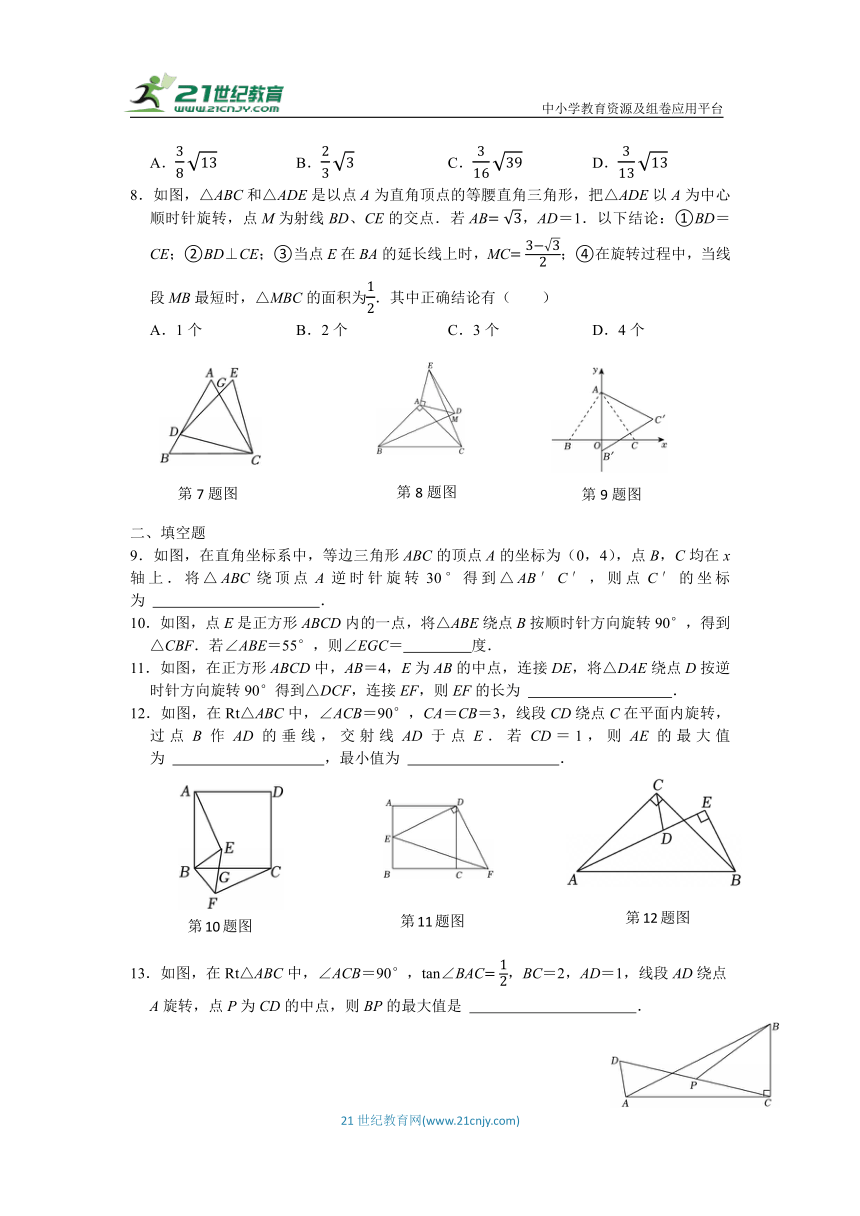
8.如图,△ABC和△ADE是以点A为直角顶点的等腰直角三角形,把△ADE以A为中心顺时针旋转,点M为射线BD、CE的交点.若AB,AD=1.以下结论:①BD=CE;②BD⊥CE;③当点E在BA的延长线上时,MC;④在旋转过程中,当线段MB最短时,△MBC的面积为.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在直角坐标系中,等边三角形ABC的顶点A的坐标为(0,4),点B,C均在x轴上.将△ABC绕顶点A逆时针旋转30°得到△AB′C′,则点C′的坐标为 .
10.如图,点E是正方形ABCD内的一点,将△ABE绕点B按顺时针方向旋转90°,得到△CBF.若∠ABE=55°,则∠EGC= 度.
11.如图,在正方形ABCD中,AB=4,E为AB的中点,连接DE,将△DAE绕点D按逆时针方向旋转90°得到△DCF,连接EF,则EF的长为 .
12.如图,在Rt△ABC中,∠ACB=90°,CA=CB=3,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若CD=1,则AE的最大值为 ,最小值为 .
13.如图,在Rt△ABC中,∠ACB=90°,tan∠BAC,BC=2,AD=1,线段AD绕点A旋转,点P为CD的中点,则BP的最大值是 .
三、解答题
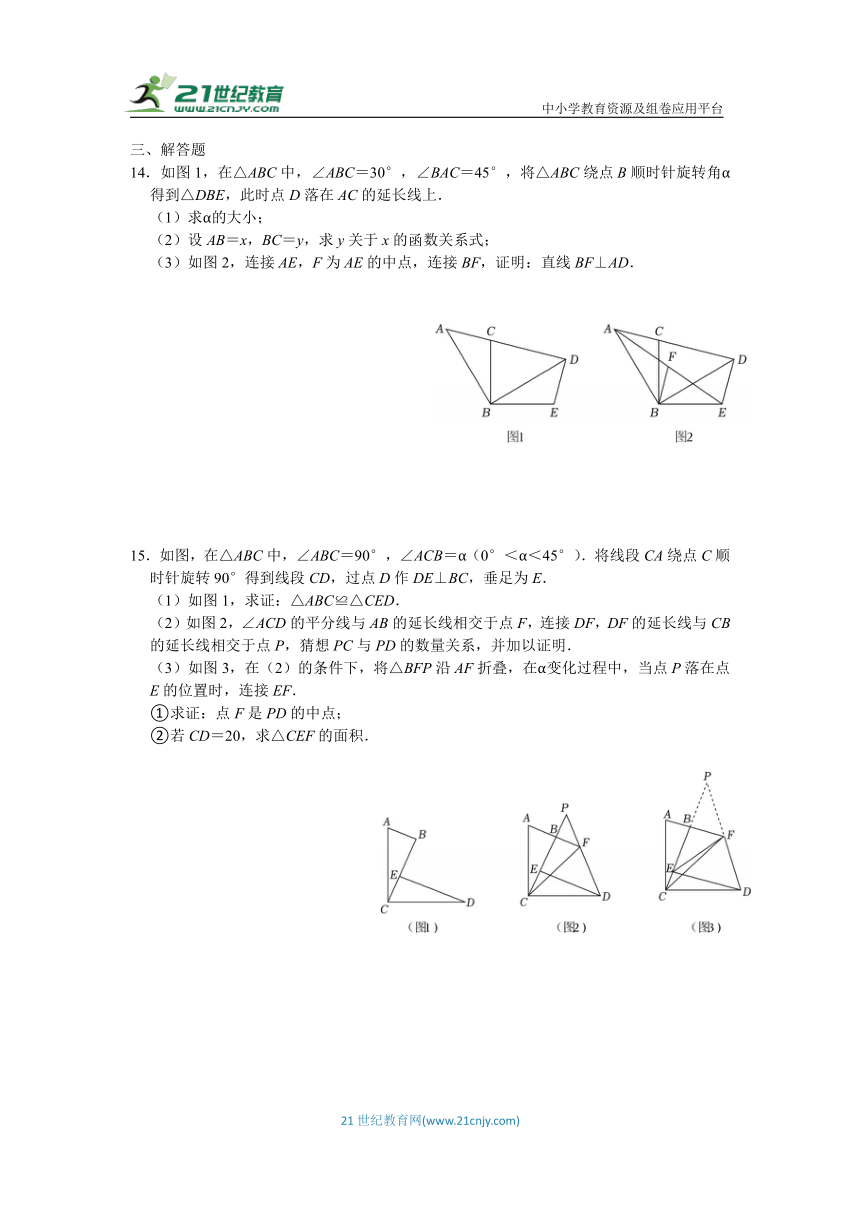
14.如图1,在△ABC中,∠ABC=30°,∠BAC=45°,将△ABC绕点B顺时针旋转角α得到△DBE,此时点D落在AC的延长线上.
(1)求α的大小;
(2)设AB=x,BC=y,求y关于x的函数关系式;
(3)如图2,连接AE,F为AE的中点,连接BF,证明:直线BF⊥AD.
15.如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
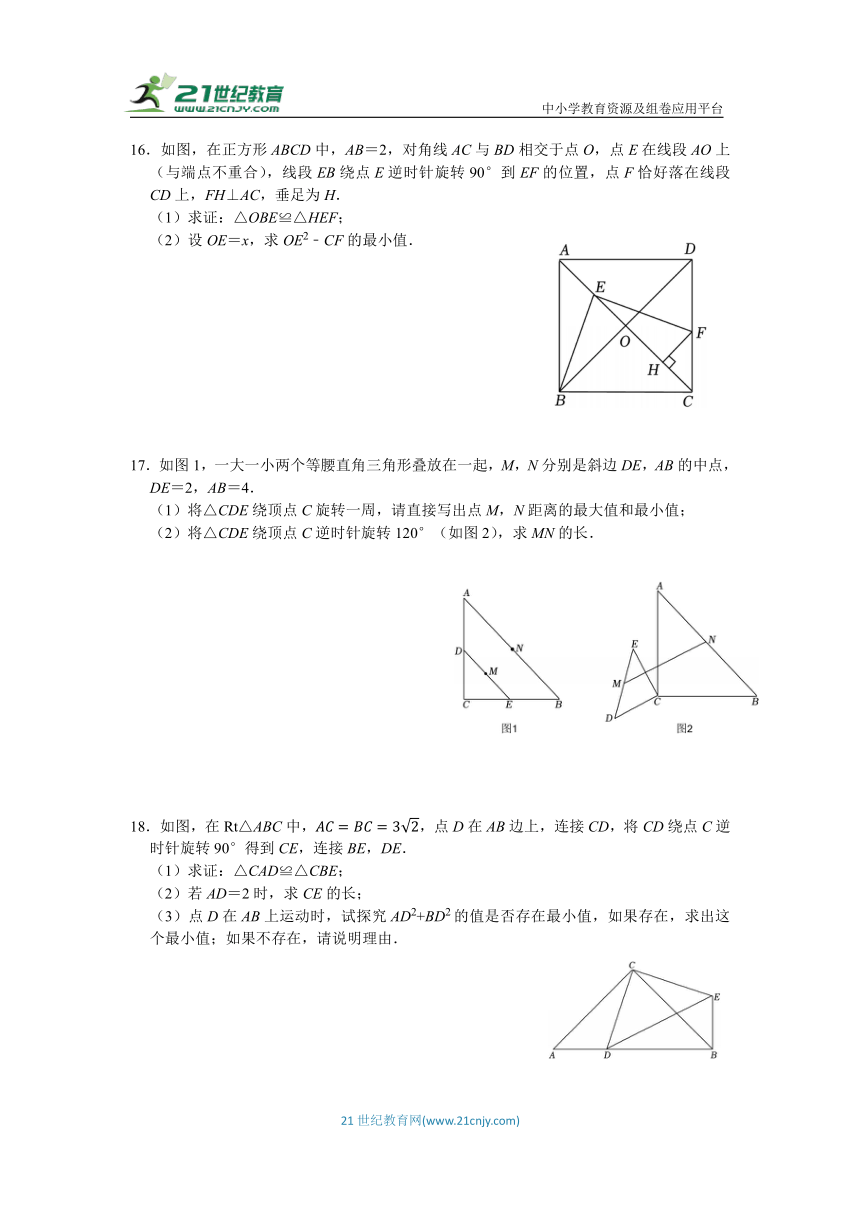
16.如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
17.如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
18.如图,在Rt△ABC中,,点D在AB边上,连接CD,将CD绕点C逆时针旋转90°得到CE,连接BE,DE.
(1)求证:△CAD≌△CBE;
(2)若AD=2时,求CE的长;
(3)点D在AB上运动时,试探究AD2+BD2的值是否存在最小值,如果存在,求出这个最小值;如果不存在,请说明理由.
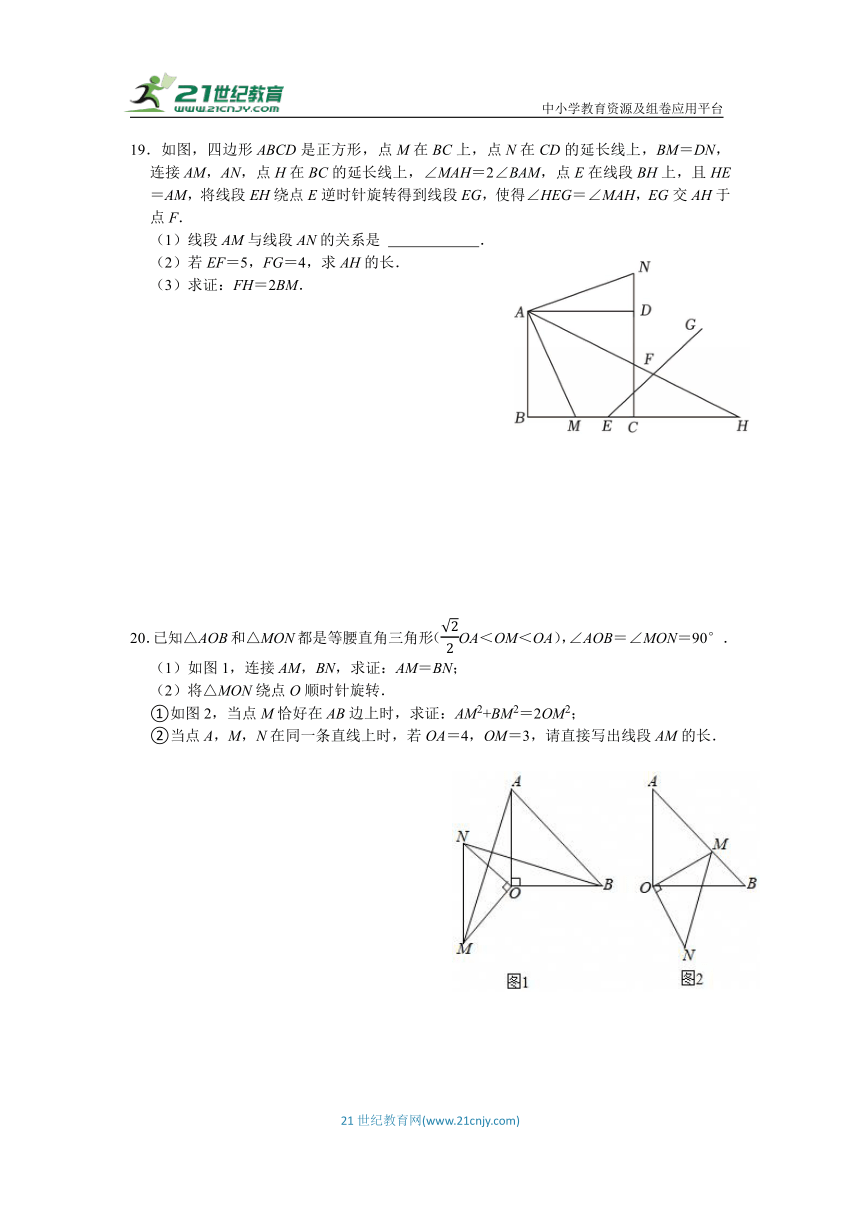
19.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,BM=DN,连接AM,AN,点H在BC的延长线上,∠MAH=2∠BAM,点E在线段BH上,且HE=AM,将线段EH绕点E逆时针旋转得到线段EG,使得∠HEG=∠MAH,EG交AH于点F.
(1)线段AM与线段AN的关系是 .
(2)若EF=5,FG=4,求AH的长.
(3)求证:FH=2BM.
20.已知△AOB和△MON都是等腰直角三角形(OA<OM<OA),∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:AM=BN;
(2)将△MON绕点O顺时针旋转.
①如图2,当点M恰好在AB边上时,求证:AM2+BM2=2OM2;
②当点A,M,N在同一条直线上时,若OA=4,OM=3,请直接写出线段AM的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 B B A A B B C D
1.【解答】解:由题意可得:
∴AB=AB′,∠BAB′=150°,
∴∠B=∠AB′B=(180°﹣150°)÷2=15°,
∴∠AB′C′=∠B=15°,∠B′AC′=∠BAC=100°,
∴∠C′=180°﹣100°﹣15°=65°,
故选:B.
2.【解答】解:∵∠AOB=90°,OA=OB=6,
∴AB6,
由旋转的性质得到:A′B′=AB=6,OA′=OA,OB′=OB,∠A′OB′=∠AOB=90°,
∴OA′=OB′,
∵△AOB绕点O顺时针旋转45°,
∴∠BOB′=45°,
∴∠BOA′=90°﹣45°=45°,
∴∠BOB′=∠BOA′,
∵OA′=OB′,
∴D是A′B′的中点,
∴ODA′B′63.
故选:B.
3.【解答】解:如图,连接BD,
∵将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,
∴∠BCD=90°,AB=AD,∠BAD=90°,
又CD=3,BC=1,
∴BD,
∴AD,
故选:A.
4.【解答】解:过点A作AG⊥BD于点G,
∵∠ABD=30°,∠A=105°,
∴∠ADB=45°,
设AE=BE=a,则AB=2a,
∴,BG,
∴DG=AG=a,
∴AD,
∵,,
∴,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴∠ADE=∠ABD=30°,
∵∠ADC=∠ADB+∠CDB=90°=∠ADE+∠EDF+∠CDF,
∴90°=30°+∠EDF+30°,
∴∠EDF=30°=∠ADE,
∵AD=CD=DF,DE=DE,
∴△ADE≌△FDE(SAS),
∴EF=AE=BE=1,
过点E作EH⊥BD于点H,
∴EH,BD,
∴△BED的面积,
故选:A.
5.【解答】解:过点N′作EF∥AB,交AD、BC于E、F,过点M作MG⊥EF于点G,
∵矩形ABCD,
∴AB∥CD,
∴AB∥EF∥CD,
∴四边形AMGE和BMGF都是矩形,
∴∠A=∠MGN'=90°,
由旋转的性质得∠NMN'=90°,MN=MN′,
∴∠AMN=90°﹣∠NMG=∠GMN′,
∴△AMN≌△GMN′(AAS),
∴MG=AM,
∴点N'在平行于AB,且与AB的距离为5的直线上运动,
作点M关于直线EF的对称点M',连接MB交直线EF于点N′,此时△MBN′周长取得最小值,
最小值为BM+BM′,
∵BMAB=5,MM′=5+5=10,
∴,
故选:B.
6.【解答】解:如图所示,
分别过点A和点B作x轴的垂线,垂足分别为M和N,
由旋转可知,
OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.
在△AOM和△OBN中,
,
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(﹣4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).
故选:B.
7.【解答】解:过D作DM⊥BC于M,
∴∠DMB=∠DMC=90°,
∵△ABC是等边三角形,
∴∠B=60°,
∵BD,
∴BM,DMBD,
∴CM=BC﹣MB=2,
∴CD,
∵将CD绕点C按顺时针方向旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴△CDE是等边三角形,
∴DE=CD=CE,∠DCE=60°,
∴∠BCD=∠ECG,
∵∠B=∠E=60°,
∴△BCD∽△ECG,
∴,
∴,
∴EG,
∴DG=DE﹣EG,
过G作GH⊥CD于H,
∴GHDG,
故选:C.
8.【解答】解:∵△ABC和△ADE是以点A为直角顶点的等腰直角三角形,
∴BA=CA,DA=EA,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,故①正确;
设∠ABD=∠ACE=x,∠DBC=45°﹣x,
∴∠EMB=∠DBC+∠BCM=∠DBC+∠BCA+∠ACE=45°﹣x+45°+x=90°,
∴BD⊥CE,故②正确;
当点E在BA的延长线上时,如图:
同理可得∠DMC=90°,
∴∠DMC=∠EAC,
∵∠DCM=∠ECA,
∴△DCM∽△ECA
∴,
∵AC,AD=1=AE,
∴,,
∴,
∴,故③正确;
④以A为圆心,AD为半径画圆,如图:
∵∠BMC=90°,
∴当CE在⊙A的下方与⊙A相切时,MB的值最小,
∴∠ADM=∠DME=∠AEM=90°,
∵AE=AD,
∴四边形AEMD是正方形,
∴MD=AE=1,
∵BD,
∴CE=BD,BM=BD﹣MD1,
∴MC=CE+ME1,
∵BCAB,
∴MB1,
∴△MBC的面积为(1)×(1),故④正确,
故选:D.
二、填空题
9.【解答】解:作C′F⊥AO,交y轴于点F,
由题可得:OA=4,
∵△ABC是等边三角形,AO⊥BC,
∴AO是∠BAC的角平分线,
∴∠OAC=30°,
∴,
在Rt△AOC中,AO2+OC2=AC2,
即,
解得,
∴,
,
,
∴,
故答案为:.
10.【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵∠ABE=55°,
∴∠EBC=∠ABC﹣∠ABE=35°,
由旋转得:BE=BF,∠EBF=90°,
∴∠BEF=∠BFE=45°,
∵∠EGC是△BEG的一个外角,
∴∠EGC=∠BEF+∠EBC=80°,
故答案为:80.
11.【解答】解:∵四边形ABCD为正方形,
∴AD=AB=4,∠A=90°,
∵E为AB的中点,
∴AE=2,
∴DE2,
∵△DAE绕点D按逆时针方向旋转90°得到△DCF,
∴DE=DF=2,∠EDF=90°,
∴△DEF为等腰直角三角形,
∴EFDE22.
故答案为:2.
12.【解答】解:∵BE⊥AE,
∴∠BEA=90°,
∴点E是在以AB为直径的圆上运动,
∵CD=1,且CD是绕点C旋转,
∴点D是在以C为圆心,以1为半径的圆上运动,
∵ABAC=3,
∴当cos∠BAE最大时,AE最大,当cos∠BAE最小时,AE最小.
①如图,当AE与圆C相切于点D,且D在△ABC内部时,∠BAE最小,AE最大,
∵∠ADC=∠CDE=90°,
∴AD2,
∵,
∴∠CEA=∠CBA=45°,
∴DE=CD=1,
此时AE=21,即AE的最大值为21,
②如图,当AE与圆C相切于点D,且D在△ABC外部时,∠BAE最大,AE最小,
同理可得AD=2,DE=1,
此时AE=21,即AE的最小值为21,
故答案为:21;21.
13.【解答】解:作AC的中点Q.连结PQ,作以Q为圆心PQ为半径的圆.
∵P是CD的中点,Q是AC的中点,
∴PQ是△ACD的中位线,
∴PQAD.
∴线段AD绕点A旋转时,点P在以Q为圆心PQ为半径的圆上移动,
∴当BP经过点Q时BP的值最大.
∵BC=2,tan∠BAC,
∴AC=4,
∴AQ=CQ=2.
∵BQ2=BC2+CQ2=8,
∴BQ=2(负数不合题意舍去).
∴BP的最大值为2.
故答案为:2.
三、解答题
14.【解答】解:(1)由旋转可得BA=BD,
又∵点D落在AC的延长线上,∠BAC=45°,
∴∠BDA=∠BAC=45°,
∴α=∠ABD=90°,
(2)如图1,过点C作CG⊥AB于点G,
∵∠BAC=45°,则△ACG是等腰直角三角形,
∴AG=CG,
∵∠ABC=30°,AB=x,BC=y,
∴,,
∵,
∴,
(3)证明:如图2,连接DF,
∵∠BDA=∠A=45°,由旋转可得∠BDE=∠BAC=45°,
∴∠DAE=90°,
∴DE⊥AD,
∵F是AE的中点,
∴DF=AF,
在△ABF和△DBF中,
,
∴△ABF≌△DBF(SSS),
∴,
∴∠FDB=∠BDE=45°,
∴BF∥DE,
∴BF⊥AD.
15.【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PFPD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BFDEb,
∴S△CEF,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF,
∴△CEF的面积是30.
16.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC,∠ACD=45°,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB,
∴FH=CH=x,
∴CFFHx,
∴OE2﹣CF=x2x=(x)2,
∵点E在线段AO上(与端点不重合),
∴0<x,
∴当x时,OE2﹣CF的最小值是.
17.【解答】解:(1)以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交圆于M2,
∵△ACB是等腰直角三角形,N是AB中点,
∴CN平分∠ACB,CNAB4=2,
∵△DCE是等腰直角三角形,
∴M1是DE中点,
∴CM1DE2=1,
∴M、N距离的最小值是NM1=CN﹣CM1=2﹣1=1,M、N距离的最大值是NM2=CN+CM2=2+1=3.
(2)连接CM,CN,作NH⊥MC交MC延长线于H,
∵△ACB是等腰直角三角形,N是AB中点,
∴CNAB=2,
同理:CMDE=1,
∵△CDE绕顶点C逆时针旋转120°,
∴∠MCN=120°,
∴∠NCH=180°﹣∠MCN=60°,
∴CHCN=1,
∴NHCH,
∵MH=MC+CH=2,
∴MN.
18.【解答】(1)证明:由题意,可知∠ACB=∠DCE=90°,CA=CB,CD=CE.
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB.
即∠ACD=∠BCE.
在△CAD和△CBE中,
∴△CAD≌△CBE(SAS);
(2)解:∵在 Rt△ABC中,,
∴∠CAB=∠CBA=45°,,
∴BD=AB﹣AD=6﹣2=4.
∵△CAD≌△CBE(SAS),
∴BE=AD=2,∠CBE=∠CAD=45°,
∴∠ABE=∠ABC+∠CBE=90°.
∴,
∴在 Rt△CDE 中,;
(3)解:存在,理由:
由(2)可知,AD2+BD2=BE2+BD2=DE2=2CD2,
∴当CD最小时,有 AD2+BD2 的值最小,此时 CD⊥AB.
∵△ABC 为等腰直角三角形,
∴,
∴AD2+BD2=2CD2≥2×32=18.
即 AD2+BD2 的最小值为18.
19.【解答】(1)解:∵四边形ABCD是正方形,
∴∠ADN=∠ADC=∠B=90°,AD=AB,
∵BM=DN,
∴△ADN≌△ABM(SAS),
∴BM=CN,∠DAN=∠BAM,
∴∠DAN+∠DAM=∠BAM+∠DAM=∠BAD=90°,
∴∠MAN=90°,
∴AM⊥AN,
故答案为:垂直且相等;
(2)解:∵∠H=∠H,∠HEG=∠MAH,
∴△HEF∽△HAM,
∴,
∵线段EH绕点E逆时针旋转得到线段EG,
∴EH=EG=EF+FG=9,
∴AM=HE=9,
∴,
∴AH;
(3)证明:如图,
延长MB至X,使BX=BM,作∠AMR=∠H,交AX于R,
∴XM=2BM,
∵AB⊥XM,
∴AX=AM,
∴∠XAB=∠BAM,∠X=∠AMB,
设∠XAB=∠BAM=α,
∴∠MAH=∠XAM=∠HEF=2α,∠X=∠AMB=90°﹣α,
∴∠AMR=∠H=90°﹣∠BAH=90°﹣3α,
∴∠MRX=∠XAM+∠AMR=2α+(90°﹣3α)=90°﹣α,
∴∠X=∠MRX,
∴RM=XM,
∵∠XAM=∠HEF=2α,∠AMR=∠H,EH=AM,
∴△HEF≌△MAR(ASA),
∴FH=RM=XM=2BM.
20.【解答】(1)证明:如图1,
∵∠AOB=∠MON=90°,
∴∠AOB+∠AON=∠MON+∠AON,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴AM=BN;
(2)①证明:如图2,连接BN,
∵∠AOB=∠MON=90°,
∴∠AOB﹣∠BOM=∠MON﹣∠BOM,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴∠MAO=∠NBO=45°,AM=BN,
∴∠MBN=90°,
∴MB2+BN2=MN2,
∵△MON是等腰直角三角形,
∴MN2=2ON2,
∴AM2+BM2=2OM2;
②解:如图3,
当点N在线段AM上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x﹣3)2+x2=(4)2,
解得:x,
∴AM=BN,
如图4,
当点M在线段AN上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x+3)2+x2=(4)2,
解得:x,
∴AM=BN,
综上所述,线段AM的长为或.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺图形的旋转的综合练习
一、选择题
1.如图,将△ABC绕点A逆时针旋转α°得到△AB'C'.当点B,C,B'在同一直线上,∠BAC=100°,α=150时,∠C'=( )
A.60° B.65° C.70° D.75°
2.如图,在△AOB中,∠AOB=90°,OA=OB=6.将△AOB绕点O顺时针旋转45°,得到△A'OB',A'B'与OB相交于点D,则OD的长为( )
A.2 B.3 C.2 D.3
3.如图,将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,若CD=3,BC=1,则AD的长为( )
A. B. C.2 D.
4.如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD,将线段DC绕点D顺时针旋转30°得到线段DF,点E为AB的中点,连接EF,ED.若EF=1,则△BED的面积是( )
A. B. C. D.
5.如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
6.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
7.如图,等边△ABC的边长为2,点D在AB上,BD,连接CD,将CD绕点C按顺时针方向旋转60°得到CE,连接DE交AC于点G.则点G到CD的距离为( )
A. B. C. D.
8.如图,△ABC和△ADE是以点A为直角顶点的等腰直角三角形,把△ADE以A为中心顺时针旋转,点M为射线BD、CE的交点.若AB,AD=1.以下结论:①BD=CE;②BD⊥CE;③当点E在BA的延长线上时,MC;④在旋转过程中,当线段MB最短时,△MBC的面积为.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在直角坐标系中,等边三角形ABC的顶点A的坐标为(0,4),点B,C均在x轴上.将△ABC绕顶点A逆时针旋转30°得到△AB′C′,则点C′的坐标为 .
10.如图,点E是正方形ABCD内的一点,将△ABE绕点B按顺时针方向旋转90°,得到△CBF.若∠ABE=55°,则∠EGC= 度.
11.如图,在正方形ABCD中,AB=4,E为AB的中点,连接DE,将△DAE绕点D按逆时针方向旋转90°得到△DCF,连接EF,则EF的长为 .
12.如图,在Rt△ABC中,∠ACB=90°,CA=CB=3,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若CD=1,则AE的最大值为 ,最小值为 .
13.如图,在Rt△ABC中,∠ACB=90°,tan∠BAC,BC=2,AD=1,线段AD绕点A旋转,点P为CD的中点,则BP的最大值是 .
三、解答题
14.如图1,在△ABC中,∠ABC=30°,∠BAC=45°,将△ABC绕点B顺时针旋转角α得到△DBE,此时点D落在AC的延长线上.
(1)求α的大小;
(2)设AB=x,BC=y,求y关于x的函数关系式;
(3)如图2,连接AE,F为AE的中点,连接BF,证明:直线BF⊥AD.
15.如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
16.如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
17.如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
18.如图,在Rt△ABC中,,点D在AB边上,连接CD,将CD绕点C逆时针旋转90°得到CE,连接BE,DE.
(1)求证:△CAD≌△CBE;
(2)若AD=2时,求CE的长;
(3)点D在AB上运动时,试探究AD2+BD2的值是否存在最小值,如果存在,求出这个最小值;如果不存在,请说明理由.
19.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,BM=DN,连接AM,AN,点H在BC的延长线上,∠MAH=2∠BAM,点E在线段BH上,且HE=AM,将线段EH绕点E逆时针旋转得到线段EG,使得∠HEG=∠MAH,EG交AH于点F.
(1)线段AM与线段AN的关系是 .
(2)若EF=5,FG=4,求AH的长.
(3)求证:FH=2BM.
20.已知△AOB和△MON都是等腰直角三角形(OA<OM<OA),∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:AM=BN;
(2)将△MON绕点O顺时针旋转.
①如图2,当点M恰好在AB边上时,求证:AM2+BM2=2OM2;
②当点A,M,N在同一条直线上时,若OA=4,OM=3,请直接写出线段AM的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 B B A A B B C D
1.【解答】解:由题意可得:
∴AB=AB′,∠BAB′=150°,
∴∠B=∠AB′B=(180°﹣150°)÷2=15°,
∴∠AB′C′=∠B=15°,∠B′AC′=∠BAC=100°,
∴∠C′=180°﹣100°﹣15°=65°,
故选:B.
2.【解答】解:∵∠AOB=90°,OA=OB=6,
∴AB6,
由旋转的性质得到:A′B′=AB=6,OA′=OA,OB′=OB,∠A′OB′=∠AOB=90°,
∴OA′=OB′,
∵△AOB绕点O顺时针旋转45°,
∴∠BOB′=45°,
∴∠BOA′=90°﹣45°=45°,
∴∠BOB′=∠BOA′,
∵OA′=OB′,
∴D是A′B′的中点,
∴ODA′B′63.
故选:B.
3.【解答】解:如图,连接BD,
∵将△ABC绕点A顺时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上,
∴∠BCD=90°,AB=AD,∠BAD=90°,
又CD=3,BC=1,
∴BD,
∴AD,
故选:A.
4.【解答】解:过点A作AG⊥BD于点G,
∵∠ABD=30°,∠A=105°,
∴∠ADB=45°,
设AE=BE=a,则AB=2a,
∴,BG,
∴DG=AG=a,
∴AD,
∵,,
∴,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴∠ADE=∠ABD=30°,
∵∠ADC=∠ADB+∠CDB=90°=∠ADE+∠EDF+∠CDF,
∴90°=30°+∠EDF+30°,
∴∠EDF=30°=∠ADE,
∵AD=CD=DF,DE=DE,
∴△ADE≌△FDE(SAS),
∴EF=AE=BE=1,
过点E作EH⊥BD于点H,
∴EH,BD,
∴△BED的面积,
故选:A.
5.【解答】解:过点N′作EF∥AB,交AD、BC于E、F,过点M作MG⊥EF于点G,
∵矩形ABCD,
∴AB∥CD,
∴AB∥EF∥CD,
∴四边形AMGE和BMGF都是矩形,
∴∠A=∠MGN'=90°,
由旋转的性质得∠NMN'=90°,MN=MN′,
∴∠AMN=90°﹣∠NMG=∠GMN′,
∴△AMN≌△GMN′(AAS),
∴MG=AM,
∴点N'在平行于AB,且与AB的距离为5的直线上运动,
作点M关于直线EF的对称点M',连接MB交直线EF于点N′,此时△MBN′周长取得最小值,
最小值为BM+BM′,
∵BMAB=5,MM′=5+5=10,
∴,
故选:B.
6.【解答】解:如图所示,
分别过点A和点B作x轴的垂线,垂足分别为M和N,
由旋转可知,
OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.
在△AOM和△OBN中,
,
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(﹣4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).
故选:B.
7.【解答】解:过D作DM⊥BC于M,
∴∠DMB=∠DMC=90°,
∵△ABC是等边三角形,
∴∠B=60°,
∵BD,
∴BM,DMBD,
∴CM=BC﹣MB=2,
∴CD,
∵将CD绕点C按顺时针方向旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴△CDE是等边三角形,
∴DE=CD=CE,∠DCE=60°,
∴∠BCD=∠ECG,
∵∠B=∠E=60°,
∴△BCD∽△ECG,
∴,
∴,
∴EG,
∴DG=DE﹣EG,
过G作GH⊥CD于H,
∴GHDG,
故选:C.
8.【解答】解:∵△ABC和△ADE是以点A为直角顶点的等腰直角三角形,
∴BA=CA,DA=EA,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,故①正确;
设∠ABD=∠ACE=x,∠DBC=45°﹣x,
∴∠EMB=∠DBC+∠BCM=∠DBC+∠BCA+∠ACE=45°﹣x+45°+x=90°,
∴BD⊥CE,故②正确;
当点E在BA的延长线上时,如图:
同理可得∠DMC=90°,
∴∠DMC=∠EAC,
∵∠DCM=∠ECA,
∴△DCM∽△ECA
∴,
∵AC,AD=1=AE,
∴,,
∴,
∴,故③正确;
④以A为圆心,AD为半径画圆,如图:
∵∠BMC=90°,
∴当CE在⊙A的下方与⊙A相切时,MB的值最小,
∴∠ADM=∠DME=∠AEM=90°,
∵AE=AD,
∴四边形AEMD是正方形,
∴MD=AE=1,
∵BD,
∴CE=BD,BM=BD﹣MD1,
∴MC=CE+ME1,
∵BCAB,
∴MB1,
∴△MBC的面积为(1)×(1),故④正确,
故选:D.
二、填空题
9.【解答】解:作C′F⊥AO,交y轴于点F,
由题可得:OA=4,
∵△ABC是等边三角形,AO⊥BC,
∴AO是∠BAC的角平分线,
∴∠OAC=30°,
∴,
在Rt△AOC中,AO2+OC2=AC2,
即,
解得,
∴,
,
,
∴,
故答案为:.
10.【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵∠ABE=55°,
∴∠EBC=∠ABC﹣∠ABE=35°,
由旋转得:BE=BF,∠EBF=90°,
∴∠BEF=∠BFE=45°,
∵∠EGC是△BEG的一个外角,
∴∠EGC=∠BEF+∠EBC=80°,
故答案为:80.
11.【解答】解:∵四边形ABCD为正方形,
∴AD=AB=4,∠A=90°,
∵E为AB的中点,
∴AE=2,
∴DE2,
∵△DAE绕点D按逆时针方向旋转90°得到△DCF,
∴DE=DF=2,∠EDF=90°,
∴△DEF为等腰直角三角形,
∴EFDE22.
故答案为:2.
12.【解答】解:∵BE⊥AE,
∴∠BEA=90°,
∴点E是在以AB为直径的圆上运动,
∵CD=1,且CD是绕点C旋转,
∴点D是在以C为圆心,以1为半径的圆上运动,
∵ABAC=3,
∴当cos∠BAE最大时,AE最大,当cos∠BAE最小时,AE最小.
①如图,当AE与圆C相切于点D,且D在△ABC内部时,∠BAE最小,AE最大,
∵∠ADC=∠CDE=90°,
∴AD2,
∵,
∴∠CEA=∠CBA=45°,
∴DE=CD=1,
此时AE=21,即AE的最大值为21,
②如图,当AE与圆C相切于点D,且D在△ABC外部时,∠BAE最大,AE最小,
同理可得AD=2,DE=1,
此时AE=21,即AE的最小值为21,
故答案为:21;21.
13.【解答】解:作AC的中点Q.连结PQ,作以Q为圆心PQ为半径的圆.
∵P是CD的中点,Q是AC的中点,
∴PQ是△ACD的中位线,
∴PQAD.
∴线段AD绕点A旋转时,点P在以Q为圆心PQ为半径的圆上移动,
∴当BP经过点Q时BP的值最大.
∵BC=2,tan∠BAC,
∴AC=4,
∴AQ=CQ=2.
∵BQ2=BC2+CQ2=8,
∴BQ=2(负数不合题意舍去).
∴BP的最大值为2.
故答案为:2.
三、解答题
14.【解答】解:(1)由旋转可得BA=BD,
又∵点D落在AC的延长线上,∠BAC=45°,
∴∠BDA=∠BAC=45°,
∴α=∠ABD=90°,
(2)如图1,过点C作CG⊥AB于点G,
∵∠BAC=45°,则△ACG是等腰直角三角形,
∴AG=CG,
∵∠ABC=30°,AB=x,BC=y,
∴,,
∵,
∴,
(3)证明:如图2,连接DF,
∵∠BDA=∠A=45°,由旋转可得∠BDE=∠BAC=45°,
∴∠DAE=90°,
∴DE⊥AD,
∵F是AE的中点,
∴DF=AF,
在△ABF和△DBF中,
,
∴△ABF≌△DBF(SSS),
∴,
∴∠FDB=∠BDE=45°,
∴BF∥DE,
∴BF⊥AD.
15.【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PFPD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BFDEb,
∴S△CEF,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF,
∴△CEF的面积是30.
16.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC,∠ACD=45°,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB,
∴FH=CH=x,
∴CFFHx,
∴OE2﹣CF=x2x=(x)2,
∵点E在线段AO上(与端点不重合),
∴0<x,
∴当x时,OE2﹣CF的最小值是.
17.【解答】解:(1)以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交圆于M2,
∵△ACB是等腰直角三角形,N是AB中点,
∴CN平分∠ACB,CNAB4=2,
∵△DCE是等腰直角三角形,
∴M1是DE中点,
∴CM1DE2=1,
∴M、N距离的最小值是NM1=CN﹣CM1=2﹣1=1,M、N距离的最大值是NM2=CN+CM2=2+1=3.
(2)连接CM,CN,作NH⊥MC交MC延长线于H,
∵△ACB是等腰直角三角形,N是AB中点,
∴CNAB=2,
同理:CMDE=1,
∵△CDE绕顶点C逆时针旋转120°,
∴∠MCN=120°,
∴∠NCH=180°﹣∠MCN=60°,
∴CHCN=1,
∴NHCH,
∵MH=MC+CH=2,
∴MN.
18.【解答】(1)证明:由题意,可知∠ACB=∠DCE=90°,CA=CB,CD=CE.
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB.
即∠ACD=∠BCE.
在△CAD和△CBE中,
∴△CAD≌△CBE(SAS);
(2)解:∵在 Rt△ABC中,,
∴∠CAB=∠CBA=45°,,
∴BD=AB﹣AD=6﹣2=4.
∵△CAD≌△CBE(SAS),
∴BE=AD=2,∠CBE=∠CAD=45°,
∴∠ABE=∠ABC+∠CBE=90°.
∴,
∴在 Rt△CDE 中,;
(3)解:存在,理由:
由(2)可知,AD2+BD2=BE2+BD2=DE2=2CD2,
∴当CD最小时,有 AD2+BD2 的值最小,此时 CD⊥AB.
∵△ABC 为等腰直角三角形,
∴,
∴AD2+BD2=2CD2≥2×32=18.
即 AD2+BD2 的最小值为18.
19.【解答】(1)解:∵四边形ABCD是正方形,
∴∠ADN=∠ADC=∠B=90°,AD=AB,
∵BM=DN,
∴△ADN≌△ABM(SAS),
∴BM=CN,∠DAN=∠BAM,
∴∠DAN+∠DAM=∠BAM+∠DAM=∠BAD=90°,
∴∠MAN=90°,
∴AM⊥AN,
故答案为:垂直且相等;
(2)解:∵∠H=∠H,∠HEG=∠MAH,
∴△HEF∽△HAM,
∴,
∵线段EH绕点E逆时针旋转得到线段EG,
∴EH=EG=EF+FG=9,
∴AM=HE=9,
∴,
∴AH;
(3)证明:如图,
延长MB至X,使BX=BM,作∠AMR=∠H,交AX于R,
∴XM=2BM,
∵AB⊥XM,
∴AX=AM,
∴∠XAB=∠BAM,∠X=∠AMB,
设∠XAB=∠BAM=α,
∴∠MAH=∠XAM=∠HEF=2α,∠X=∠AMB=90°﹣α,
∴∠AMR=∠H=90°﹣∠BAH=90°﹣3α,
∴∠MRX=∠XAM+∠AMR=2α+(90°﹣3α)=90°﹣α,
∴∠X=∠MRX,
∴RM=XM,
∵∠XAM=∠HEF=2α,∠AMR=∠H,EH=AM,
∴△HEF≌△MAR(ASA),
∴FH=RM=XM=2BM.
20.【解答】(1)证明:如图1,
∵∠AOB=∠MON=90°,
∴∠AOB+∠AON=∠MON+∠AON,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴AM=BN;
(2)①证明:如图2,连接BN,
∵∠AOB=∠MON=90°,
∴∠AOB﹣∠BOM=∠MON﹣∠BOM,
即∠AOM=∠BON,
∵△AOB和△MON都是等腰直角三角形,
∴OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴∠MAO=∠NBO=45°,AM=BN,
∴∠MBN=90°,
∴MB2+BN2=MN2,
∵△MON是等腰直角三角形,
∴MN2=2ON2,
∴AM2+BM2=2OM2;
②解:如图3,
当点N在线段AM上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x﹣3)2+x2=(4)2,
解得:x,
∴AM=BN,
如图4,
当点M在线段AN上时,连接BN,设BN=x,
由(1)可知△AOM≌△BON,可得AM=BN且AM⊥BN,
在Rt△ABN中,AN2+BN2=AB2,
∵△AOB和△MON都是等腰直角三角形,OA=4,OM=3,
∴MN=3,AB=4,
∴(x+3)2+x2=(4)2,
解得:x,
∴AM=BN,
综上所述,线段AM的长为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
