2025年九年级中考数学三轮冲刺练习二次函数中线段最值问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习二次函数中线段最值问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:04:59 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习二次函数中线段最值问题
1.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于C(0,﹣4)点,点A的坐标为(﹣1,0).
(1)求抛物线的解析式及B点坐标;
(2)求△ABC的面积;
(3)点P是直线BC下方抛物线上一动点,过点P作y轴平行线交直线BC于点Q,求线段PQ的最大值及此时点P的坐标.
2.平面直角坐标系中,点O是坐标原点,抛物线与y轴交于A(0,﹣3),与x轴交于B、C两点(C在B的右侧),顶点坐标为D(2,1).
(1)求抛物线解析式;
(2)点E是抛物线上一动点,且位于直线AC的上方,过点E作AC的垂线交AC于点F,求EF长度的最大值;
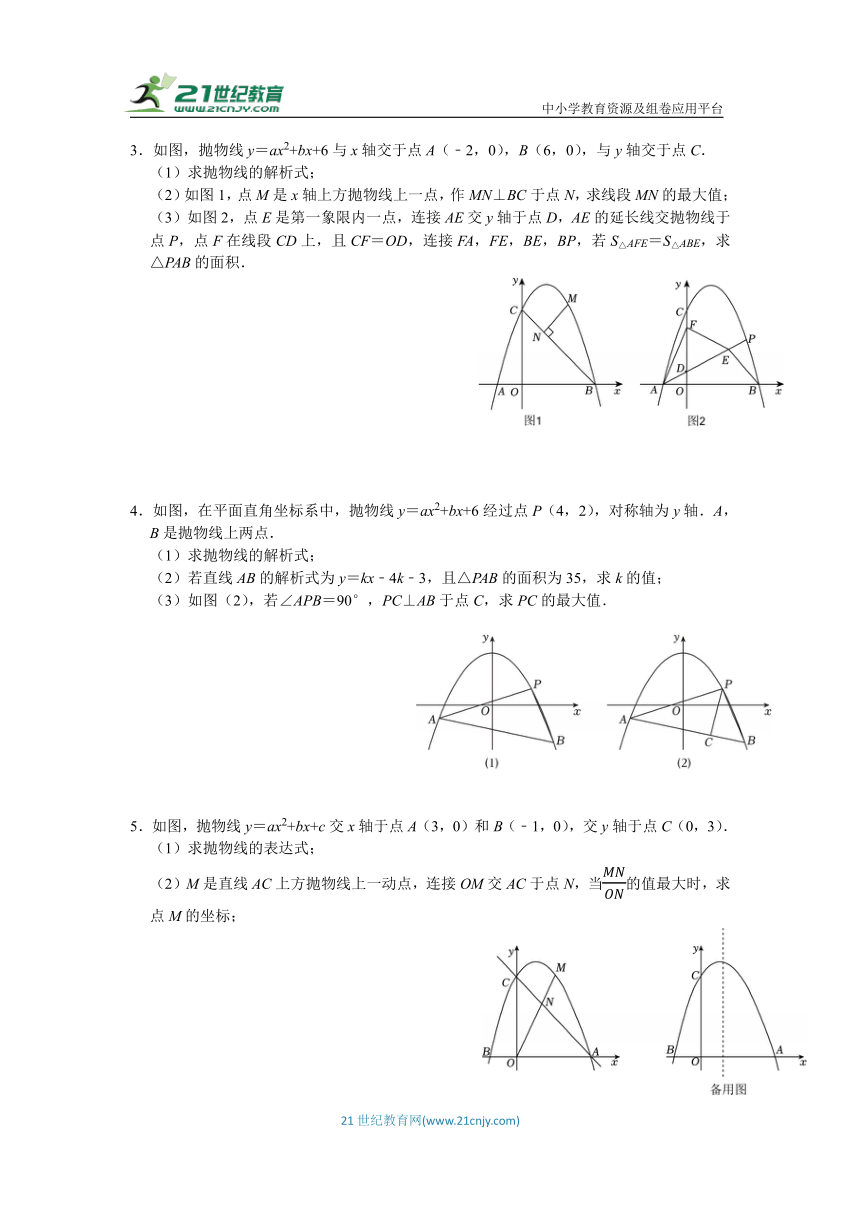
3.如图,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点M是x轴上方抛物线上一点,作MN⊥BC于点N,求线段MN的最大值;
(3)如图2,点E是第一象限内一点,连接AE交y轴于点D,AE的延长线交抛物线于点P,点F在线段CD上,且CF=OD,连接FA,FE,BE,BP,若S△AFE=S△ABE,求△PAB的面积.
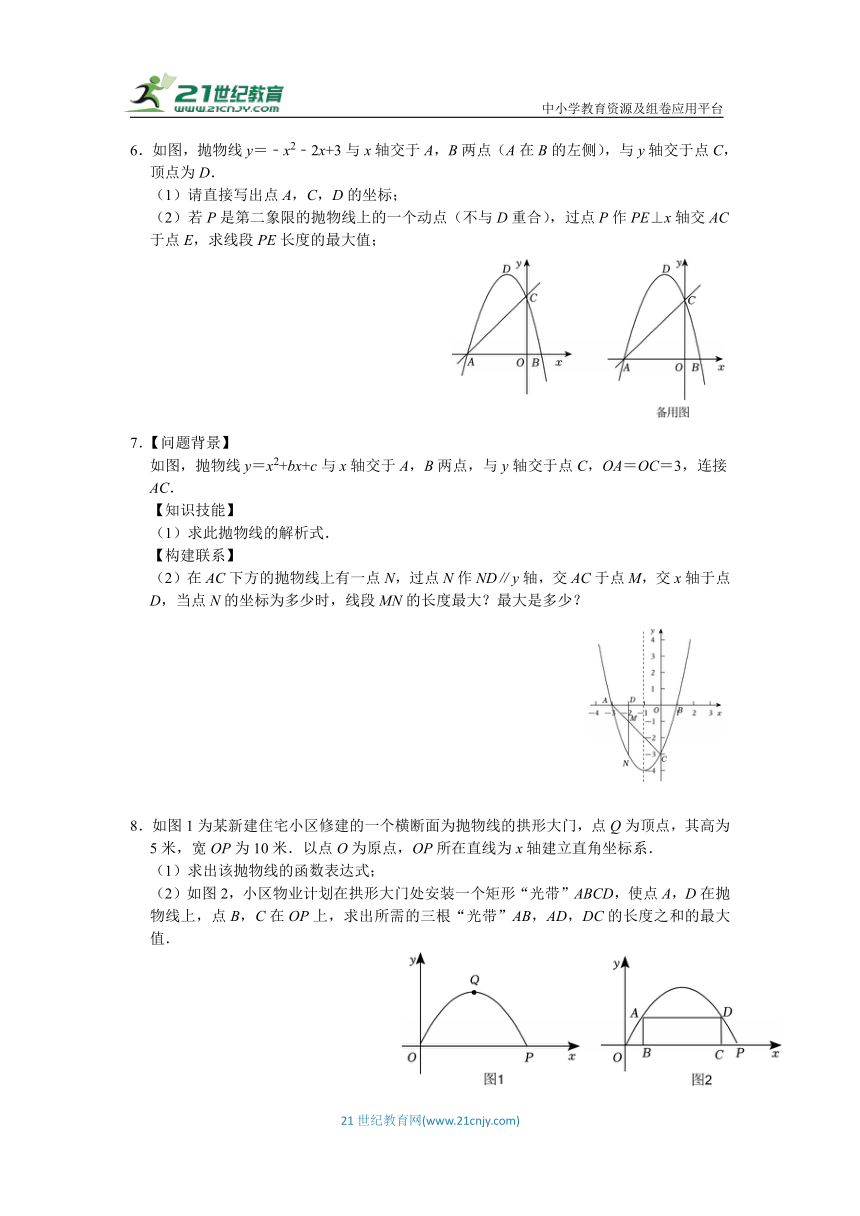
4.如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点P(4,2),对称轴为y轴.A,B是抛物线上两点.
(1)求抛物线的解析式;
(2)若直线AB的解析式为y=kx﹣4k﹣3,且△PAB的面积为35,求k的值;
(3)如图(2),若∠APB=90°,PC⊥AB于点C,求PC的最大值.
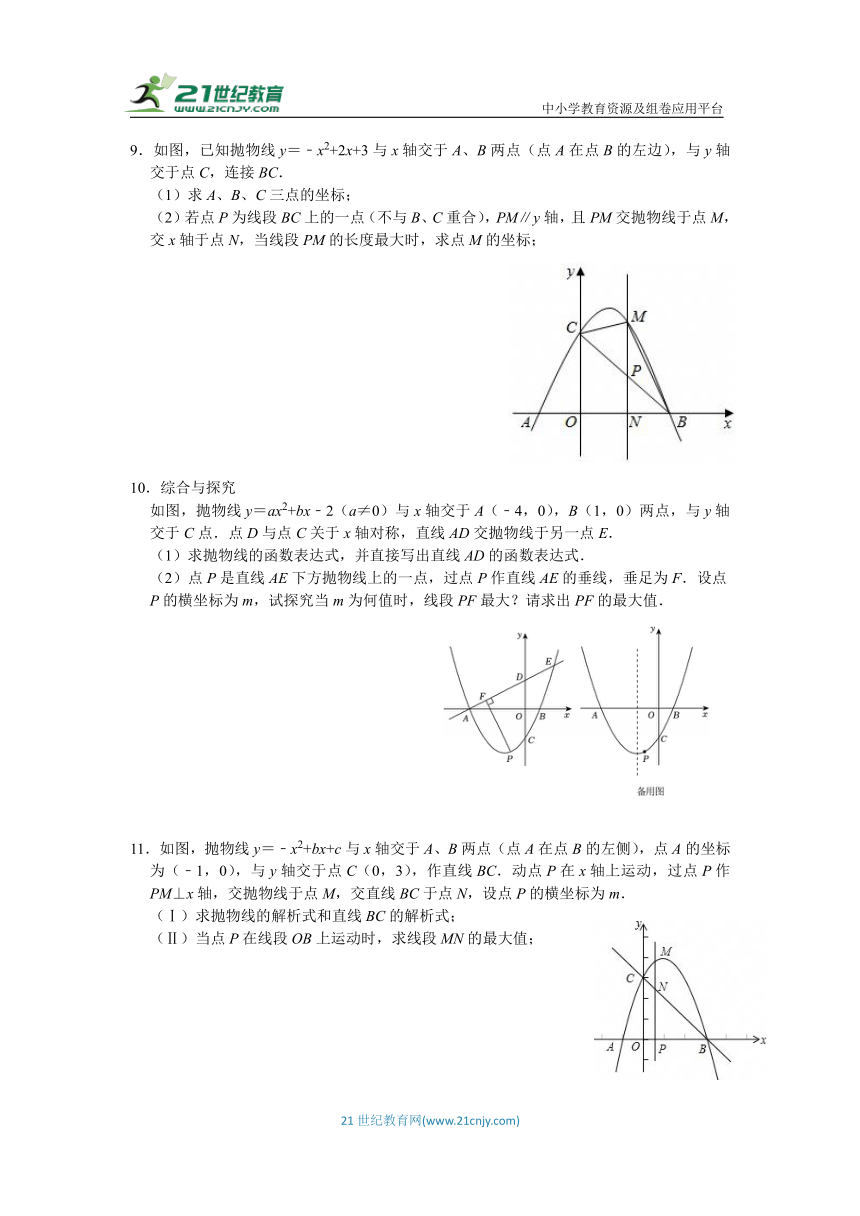
5.如图,抛物线y=ax2+bx+c交x轴于点A(3,0)和B(﹣1,0),交y轴于点C(0,3).
(1)求抛物线的表达式;
(2)M是直线AC上方抛物线上一动点,连接OM交AC于点N,当的值最大时,求点M的坐标;
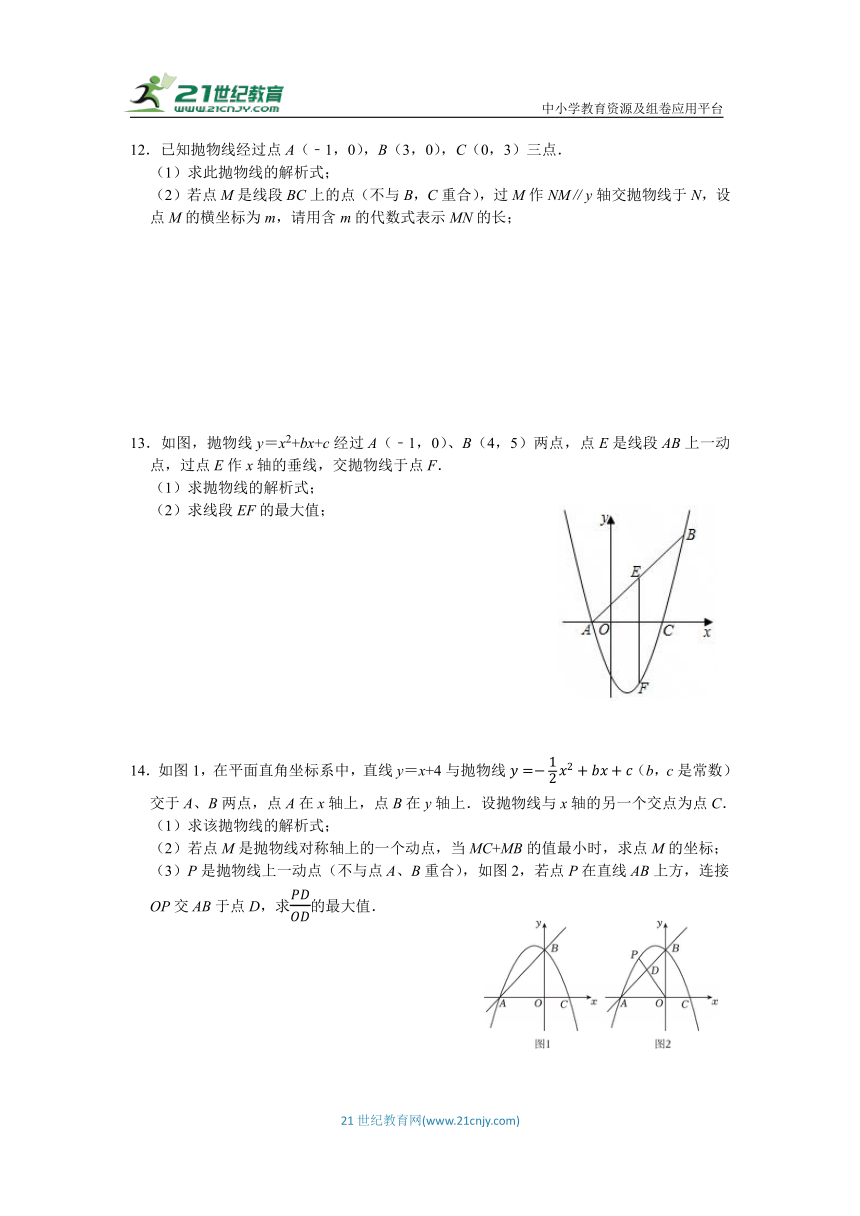
6.如图,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)若P是第二象限的抛物线上的一个动点(不与D重合),过点P作PE⊥x轴交AC于点E,求线段PE长度的最大值;
7.【问题背景】
如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,OA=OC=3,连接AC.
【知识技能】
(1)求此抛物线的解析式.
【构建联系】
(2)在AC下方的抛物线上有一点N,过点N作ND∥y轴,交AC于点M,交x轴于点D,当点N的坐标为多少时,线段MN的长度最大?最大是多少?
8.如图1为某新建住宅小区修建的一个横断面为抛物线的拱形大门,点Q为顶点,其高为5米,宽OP为10米.以点O为原点,OP所在直线为x轴建立直角坐标系.
(1)求出该抛物线的函数表达式;
(2)如图2,小区物业计划在拱形大门处安装一个矩形“光带”ABCD,使点A,D在抛物线上,点B,C在OP上,求出所需的三根“光带”AB,AD,DC的长度之和的最大值.
9.如图,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A、B、C三点的坐标;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;
10.综合与探究
如图,抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(﹣4,0),B(1,0)两点,与y轴交于C点.点D与点C关于x轴对称,直线AD交抛物线于另一点E.
(1)求抛物线的函数表达式,并直接写出直线AD的函数表达式.
(2)点P是直线AE下方抛物线上的一点,过点P作直线AE的垂线,垂足为F.设点P的横坐标为m,试探究当m为何值时,线段PF最大?请求出PF的最大值.
11.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
12.已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
13.如图,抛物线y=x2+bx+c经过A(﹣1,0)、B(4,5)两点,点E是线段AB上一动点,过点E作x轴的垂线,交抛物线于点F.
(1)求抛物线的解析式;
(2)求线段EF的最大值;
14.如图1,在平面直角坐标系中,直线y=x+4与抛物线(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
(1)求该抛物线的解析式;
(2)若点M是抛物线对称轴上的一个动点,当MC+MB的值最小时,求点M的坐标;
(3)P是抛物线上一动点(不与点A、B重合),如图2,若点P在直线AB上方,连接OP交AB于点D,求的最大值.
15.如图,抛物线与x轴相交于A(﹣3,0),B(1,0)两点,且经过点(2,5),点C为抛物线与y轴的交点.
(1)求抛物线的解析式和点C的坐标;
(2)若点P为抛物线图象上的一点,S△POC=4S△BOC,求P点的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
16.综合与探究
如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(2,0),B(0,2),连接AB,P(m,n)为抛物线AB部分上一动点(可与A,B两点重合),过点P作PN⊥x轴交直线AB于点M,交x轴于点N.
(1)求抛物线和直线AB的解析式.
(2)①求线段PM的最大值.
②连接OM,当△OBM为等腰三角形时,求m的值.
17.已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)直接写出A,B,C三点的坐标;
(2)如图1,点P为直线BC下方抛物线上一点,PD⊥BC于点D,求PD的最大值;
(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x﹣9上,求证:直线MN必经过一个定点,并求该定点坐标.
18.已知抛物线y=ax2x﹣6与x轴交于A(t,0),B(8,0)两点,与y轴交于点C,直线y=kx﹣6经过点B,点P在抛物线上,设点P的横坐标为m.
(1)填空:a= ,k= ,t= ;
(2)如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;
(3)如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求CQPQ的最大值.
19.如图,抛物线y=x2+bx﹣5与x轴交于A,B两点(点A在点B的左侧)且B(5,0),抛物线与y轴交于点C,点D为第二象限抛物线上一点,且点D的横坐标为﹣2.
(1)求抛物线的表达式.
(2)若P是y轴上一动点,当PA+PD值最小时,求点P的坐标.
(3)点M为抛物线上一动点,且横坐标为m(0<m<2),过点M作MQ∥y轴交直线BC于点Q,过点M作MN∥x轴,交抛物线于点N,求MQ+MN的最大值.
20.如图,抛物线y=ax2+bx+3交x轴于点A(3,0)和B(﹣1,0),交y轴于点C.
(1)求抛物线的表达式;
(2)D是直线AC上方抛物线上一动点,连接OD交AC于点N,当的值最大时,求点D的坐标;
参考答案
1.【解答】解:(1)把(0,﹣4),(﹣1,0),代入y=x2+bx+c得:
,
解得,
∴抛物线的表达式为y=x2﹣3x﹣4,
令x2﹣3x﹣4=0,则x=﹣1或4,
∴B(4,0);
(2)∵A(﹣1,0),B(4,0),C(0,﹣4),
∴AB=5,OC=4,
;
(3)设直线BC的解析式为yBC=kx﹣4,
∵B(4,0),
∴0=4k﹣4,
解得k=1,
∴直线BC的解析式为yBC=x﹣4,
设P(x,x2﹣3x﹣4),0<x<4,
∵PQ∥y轴,
∴Q(x,x﹣4),
∴PQ=x﹣4﹣(x2﹣3x﹣4)=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,PQmax=4,此时P(2,﹣6),
∴线段PQ的最大值是4,此时点P的坐标为(2,﹣6).
2.【解答】解:(1)∵顶点坐标为D(2,1),
设二次函数的顶点式为y=a(x﹣2)2+1,
∵抛物线与y轴交于A(0,﹣3),
∴a(0﹣2)2+1=﹣3,
解得,a=﹣1.
∴二次函数的解析式为y=﹣x2+4x﹣3;
(2)由题意,由(1)得,抛物线解析式为y=﹣x2+4x﹣3=﹣(x﹣2)2+1.
∴顶点D(2,1).
令y=0,
∴x2﹣4x+3=0.
∴x=1或3.
∴抛物线与x轴的交点B(1,0),C(3,0).
由A(0,﹣3),C(3,0)得,直线AC为y=x﹣3.
由题意,当平行于AC的直线l与抛物线相切时,EF最大.
可设直线l为y=x+m,由抛物线为y=﹣x2+4x﹣3,
∴此时方程为x+m=﹣x2+4x﹣3,
则Δ=9﹣4(3+m)=0.
∴m.
∴l为y=x,又AC为y=x﹣3,
∴(﹣3).
∵直线l与y轴夹角45°,
∴EF的最大值为.
3.【解答】解:(1)物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),将点A,点B的坐标代入得:
,
解得:,
∴抛物线的表达式为;
(2)由B(6,0),C(0,6)解得直线BC的解析式为y=﹣x+6,
过点M作MQ∥y轴交BC于点Q,如图1,
设,Q(m,﹣m+6),
,
∵∠MQN=∠OCB=45°,MN⊥BC,
∴,
∴,
∴当m=3时,MN最大,最大值是;
(3)过F作FG⊥AP于点G,过B作BH⊥AP于点H,过B作BK∥y轴交AP的延长线于点K,如图2,
∵S△AFE=S△ABE,
∴FG=BH,
又∵∠FDG=∠BKH,∠FGD=∠BHK=90°,
∴△FDG≌△BKH(AAS),
∴FD=BK,
∵,
且CF=OD,
∴OD:DF:CF=1:4:1,
∴,
∴D(0,1),
∴直线AD的解析式为,
∵,
∴,
解得x=5或﹣2(舍去),
∴,
∴△PAB的面积,
故△PAB的面积为14.
4.【解答】解:(1)∵抛物线y=ax2+bx+6经过点P(4,2),对称轴为y轴,
∴,
解得,
∴抛物线的解析式为yx2+6;
(2)∵y=kx﹣4k﹣3=k(x﹣4)﹣3,
∴直线AB过定点D(4,﹣3).
如图,连结PD,
∵P(4,2),D(4,﹣3),
∴PD∥y轴,PD=5,
∴S△ABP|xB﹣xA|=35,
∴|xB﹣xA|=14,
由kx﹣4k﹣3x2+6,
整理得x2+4kx﹣16k﹣36=0,
由根与系数的关系得xB+xA=﹣4k,xBxA=﹣16k﹣36,
∴|xB﹣xA|2=(xB+xλ)2﹣4xBxA=142,
∴4k2+16k﹣13=0,
解得k=﹣2或k=﹣2;
∴k的值为﹣2或﹣2;
(3)设A(m,m2+6),B(n,n2+6),直线AB解析式为y=tx+b',
由得x2+tx+b'﹣6=0,
由根与系数的关系得m+n=﹣4t,mn=4b'﹣24,
如图,过点P作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足为E、F,
∴∠E=90°,∠F=90°,
∴∠APE+∠PAE=90°,∠E=∠F,
∵∠APB=90°,
∴∠APE+∠BPF=90°,
∴∠PAE=∠BPF,
∴△PAE∽△BPF,
∴,
∴,
整理变形可得mn+4(m+n)+32=0,
又∵m+n=﹣4t,mn=4b'﹣24,
∴b'=4t﹣2,
∴直线AB的解析式为y=tx+4t﹣2=t(x+4)﹣2,
∴直线AB经过定点C(﹣4,﹣2),
∵P(4,2),
∴PC的最大值为4.
5.【解答】解:(1)抛物线y=ax2+bx+c交x轴于点A(3,0)和B(﹣1,0),交y轴于点C(0,3).将点A、点B、点C的坐标代入得:
,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3.
(2)如图1,过点M作MH∥y轴,交AC于点H,
设直线AC的解析式为y=kx+t,将点A、点C的坐标代入得:
,
解得:,
∴直线AC的解析式为y=﹣x+3,
设M(m,﹣m2+2m+3),则H(m,﹣m+3),
∴MH=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∵MH∥y轴,
∴△MHN∽△OCN,
∴,
∴当时,有最大值,
此时,
∴点M的坐标为.
6.【解答】解:(1)抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D,
令y=0,得:﹣x2﹣2x+3=0,
解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
令x=0,得:y=3,
∴C(0,3),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴D(﹣1,4);
(2)P是第二象限的抛物线上的一个动点(不与D重合),PE⊥x轴交AC于点E,如图1,
设直线AC的解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得,
∴y=x+3,
设P(p,﹣p2﹣2p+3)(﹣3<p<0),则E(p,p+3),
∴PE=﹣p2﹣2p+3﹣(p+3)
=﹣p2﹣3p
,
∴当时,PE有最大值为;
7.【解答】解:(1)∵OA=OC=3,
∴A(﹣3,0),C(0,﹣3),
把A(﹣3,0),C(0,﹣3)代入y=x2+bx+c,得,
,
解得,,
∴此抛物线的解析式为y=x2+2x﹣3;
(2)设直线AC的解析式为y=kx+b,
把把A(﹣3,0),C(0,﹣3)代入y=kx+b,得,
,
解得,
∴直线AC的解析式为y=﹣x﹣3;
设点N的坐标为(x,x2+2x﹣3),则点M(x,﹣x﹣3),
∴DN=﹣(x2+2x﹣3)=﹣x2﹣2x+3,DM=﹣(﹣x﹣3)=x+3,
∴,
∵﹣1<0,
∴MN有最大值,最大值为,
当x时,y=x2+2x﹣3,
∴点N的坐标为;
8.【解答】解:(1)由题意可设这条抛物线的函数解析式为y=a(x﹣5)2+5,
∵抛物线过O(0,0),
∴25a+5=0,
解得a,
∴这条抛物线的函数解析式为y(x﹣5)2+5;
(2)设点A的坐标为(m,m2+2m),
则OB=m,AB=DC2m,
根据抛物线的轴对称,可得:OB=m=CP,BC=10﹣2m,AD=10﹣2m,
令L=AB+AD+DC
2m+10﹣2m
2m+10
,
∵0,开口向下,
∴当m时,最大值为,
∴当OB米时,三根“光带”长度之和的最大值为米.
9.【解答】解:(1)对于y=﹣x2+2x+3,令x=0,则y=3,
∴C(0,3),
令y=0,则y﹣x2+2x+3=0,解得:x1=3,x2=﹣1,
∴A(﹣1,0),
∴B(3,0);
(2)设BC的表达式为y=kx+b,则,解得,
∴直线BC的表达式为y=﹣x+3,
设点P的坐标为(t,﹣t+3),则点M的坐标为(t,﹣t2+2t+3),
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t=﹣(t)2,
t时,PM最大,
此时点M坐标(,);
10.【解答】解:(1)将A(﹣4,0),B(1,0)代入y=ax2+bx﹣2(a≠0)得:,
解得:,
∴二次函数的解析式为:;
在中,当x=0时,y=﹣2,
∴C(0,﹣2),
∵点D与点C关于x轴对称,
∴D(0,2),
设直线AD的表达式为y=kx+b1,
将D(0,2),A(﹣4,0)代入解析式得:,
解得:,
∴直线AD的表达式为;
(2)存在,理由如下:
如图,过点P作y轴的平行线交AD于G,
∴∠AGP=∠ADC,
∵A(﹣4,0),D(0,2),
∴OA=4,OD=2,
∴,
∴,
∴在Rt△PFG中,,
∴,
∴当GP取得最大值时,PF取得最大值,
设点,则,
∴,
∵,
∴当m=﹣1时,GP取得最大值为,
∴PF的最大值为;
11.【解答】解:(1)∵抛物线过A、C两点,
∴代入抛物线解析式可得:,解得:,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得,解得,
∴直线BC解析式为y=﹣x+3;
(2)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,﹣m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m)2,
∴当m时,MN有最大值,MN的最大值为;
12.【解答】解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得 ;
故直线BC的解析式:y=﹣x+3.
已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
13.【解答】解:(1)把A(﹣1,0)、B(4,5)代入y=x2+bx+c,得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)设F(x,x2﹣2x﹣3)(﹣1<x<4),
设直线AB的解析式为y=kx+b,代入点A(﹣1,0)、B(4,5),得:
,
解得:,
∴直线AB的解析式为y=x+1,
∵EF∥y轴,
∴E(x,x+1),
∴EF=x+1﹣(x2﹣2x﹣3)=﹣x2+3x+4,
当x时,EF取得最大值为;
14.【解答】解:(1)∵直线y=x+4与坐标轴交于A、B两点,
当x=0时,y=4,当y=0时,x=﹣4,
∴A(﹣4,0),B(0,4),
将A、B代入抛物线,
得,
解得,
∴抛物线的解析式为y.
答:抛物线的解析式为y.
(2)∵抛物线的解析式为y.
∴当y=0时,解得x1=﹣4,x2=2,
∴抛物线的对称轴为直线x,
∵A(﹣4,0),C(2,0)关于x=﹣1对称,
如图,连接AB交对称轴于点M,
∴MB+MC=MB+MA=AB,
此时MC+MB取得最小值.
∴当x=﹣1时,y=﹣1+4=3,
∴M(﹣1,3).
答:点M的坐标为(﹣1,3).
(3)如图,过点P作PE∥OB交AB于点E,
则△PDE∽△ODB,
∴,
设点P(m,)(﹣4<m<0),
∴E(m,m+4),
∴,
∴,
∴当m时有最大值,
∴的最大值为.
答:的最大值的最大值为.
15.【解答】解:(1)∵抛物线与x轴相交于A(﹣3,0),B(1,0)两点,且经过点(2,5),
∴,
解得.
所以抛物线的解析式为:y=x2+2x﹣3;
(2)二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴3×|x|=43×1,
∴|x|=4,x=4或﹣4.
∴当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
(3)设直线AC的解析式为y=kx﹣3,将A(﹣3,0)代入,
得0=﹣3k﹣3,
解得k=﹣1.
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x)2,
∴当x时,QD有最大值.
16.【解答】解:(1)∵抛物线经过点B(0,2),
∴y=﹣x2+bx+2.
将点A(2,0)代入,得0=﹣22+2b+2,
解得:b=1,
抛物线的解析式为y=﹣x2+x+2.
设直线AB的解析式为y=kx+2,
将点A(2,0)代入,得0=2k+2,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2.
(2)①将P(m,n)代入y=﹣x2+x+2中,得n=﹣m2+m+2.
将x=m代入y=﹣x+2中,得y=﹣m+2.
∴PM=n﹣y=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m=﹣(m﹣1)2+1,
即PM的最大值为1.
②∵点M在直线AB上,且点P(m,n),
∴点M的坐标为(m,﹣m+2).
∵点B(0,2),
∴OB=2,
∴BM2=(m﹣0)2+(﹣m+2﹣2)2=2m2,
OM2=m2+(﹣m+2)2=2m2﹣4m+4.
当△OBM为等腰三角形时,
(ⅰ)若BM=OM,则BM2=OM2,
即2m2=2m2﹣4m+4,解得m=1.
(ⅱ)若BM=OB,则BM2=OB2,
即2m2=4,
解得:或(舍去).
(ⅲ)若OM=OB,则OM2=OB2,
即2m2﹣4m+4=4,
解得:m=2或m=0(舍去).
综上所述,m=1或或m=2.
17.【解答】(1)解:对于y=x2﹣2x﹣3,令y=0,则0=x2﹣2x﹣3,
∴x1=﹣1,x2=3,
∴点A(﹣1,0),点B(3,0),
令x=0,则y=﹣3,
∴点C(0,﹣3);
(2)解:过点P作PE⊥x轴于E,交BC于点F,如图1:
设直线BC的解析式为y=kx+b,
将点B(3,0),C(0,﹣3)代入y=kx+b得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
设P(x,x2﹣2x﹣3),则F(x,x﹣3),
∴PF=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∵PE⊥x轴,
∴PE∥y轴,
∴∠PFD=∠BCO,
∵∠PDF=∠BOC=90°,
∴△PDF∽△BCO,
∴,
∵B(3,0),C(0,﹣3),
∴OB=3,OC=3,
∴BC=3,
∴,
∴PDx2x,
∴当x时,PD最大为;
(3)证明:如图2,设点M(xM,yM),N(xN,yN),
直线MN:y=k′x+b′,直线CM:y=k1x+b1,直线BN:y=k2x+b2,
将点C(0,﹣3)代入直线CM的解析式得:b1=﹣3,
将点B(3,0)代入直线BN的解析式得:b2=﹣3k2,
联立直线MN与抛物线的解析式得:,
整理得:x2﹣(k′+2)x﹣b′﹣3=0,
则xM+xN=k′+2,xM xN=﹣b′﹣3,
同理:xM+xC=k1+2,xN+xB=k2+2,
∵xC=0,xB=3,
∴xM=k1+2,xN=k2﹣1,
∴k′=xM+xN﹣2=k1+2+k2﹣1﹣2=k1+k2﹣1,
b′=﹣xM xN﹣3=﹣(k1+2)(k2﹣1)﹣3=﹣k1k2﹣2k2+k1+2﹣3=﹣k1k2﹣2k2+k1﹣1,
联立直线CM与直线BN的解析式得:,
解得:,
∵直线BN与直线CM的交点始终在直线y=2x﹣9上,
∴29,
化简得:k1k2=3k1﹣2,
∴b′=﹣k1k2﹣2k2+k1﹣1=﹣3k1+2﹣2k2+k1﹣1=﹣2k1﹣2k2+1=﹣2(k1+k2)+1=﹣2(k′+1)+1=﹣2k′﹣1,
∴直线MN:y=k′x﹣2k′﹣1=k′(x﹣2)﹣1,
∴不论k′为何值,均有x=2时,y=﹣1,
即:直线MN恒过定点P(2,﹣1).
18.【解答】解:(1)将B(8,0)代入y=ax2x﹣6,
∴64a+22﹣6=0,
∴a,
∴yx2x﹣6,
当y=0时,t2t﹣6=0,
解得t=3或t=8(舍),
∴t=3,
∵B(8,0)在直线y=kx﹣6上,
∴8k﹣6=0,
解得k;
故答案为:;;3;
(2)作PM⊥x轴交于M,
∵P点横坐标为m,
∴P(m,m2m﹣6),
∴PMm2m+6,AM=m﹣3,
在Rt△COA和Rt△AMP中,
∵∠OAC+∠PAM=90°,∠APM+∠PAM=90°,
∴∠OAC=∠APM,
∴△COA∽△AMP,
∴,即OA MA=CO PM,
3(m﹣3)=6(m2m+6),
解得m=3(舍)或m=10,
∴P(10,);
(3)作PN⊥x轴交BC于N,过点N作NE⊥y轴交于E,
∴PNm2m﹣6﹣(m﹣6)m2+2m,
∵PN⊥x轴,
∴PN∥OC,
∴∠PNQ=∠OCB,
∴Rt△PQN∽Rt△BOC,
∴,
∵OB=8,OC=6,BC=10,
∴QNPN,PQPN,
由△CNE∽△CBO,
∴CNENm,
∴CQPQ=CN+NQPQ=CN+PN,
∴CQPQmm2+2mm2m(m)2,
当m时,CQPQ的最大值是.
19.【解答】解:(1)把(5,0)代入y=x2+bx﹣5中,
0=25+5b﹣5,
得b=﹣4,
∴y=x2﹣4x﹣5;
(2)在y=x2﹣4x﹣5中,
当x=﹣2时:y=7,
∴点D的坐标为(﹣2,7),
当y=0时:x1=﹣1,x2=5,
∴点A的坐标为(﹣1,0),
作点A关于y轴的对称点E,
∵A点坐标为(﹣1,0),
∴E点坐标为(1,0),
连接DE交y轴于点P,
此时PA+PD最小,
设直线DE为y=kx+b,
∴
解得:,
∴直线DE的表达式为
∴点P的坐标为;
(3)如图:
在y=x2﹣4x﹣5中,
当x=0时:y=﹣5,
∴点C的坐标为(0,﹣5),
设直线BC解析式为y=k1x+b2,则
解得,
∴直线BC表达式:y=x﹣5,
设M点坐标为(m,m2﹣4m﹣5),
Q点坐标(m,m﹣5),
∴MQ=m﹣5﹣m2+4m+5=﹣m2+5m,
∵M和N关于对称轴对称,对称轴为直线,
∴MN=2(2﹣m)=4﹣2m,
∴MN+MQ=4﹣2m+(﹣m2+5m)
=﹣m2+3m+4
,
∵﹣1<0,
∴当时MN+MQ有最大值.
20.【解答】解:(1)把点A(3,0)和B(﹣1,0)代入得:,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)过点D作DH∥y轴,交AC于点H,如图所示:
设D(m,﹣m2+2m+3),直线AC的解析式为y=kx+b,
由(1)可得:C(0,3),
∴,解得:,
∴直线AC的解析式为y=﹣x+3,
∴H(m,﹣m+3),
∴DH=﹣m2+3m,
∵DH∥y轴,
∴△OCN∽△DHN,
∴,
∵,
∴当时,的值最大,
∴;
(3)由题意可得如图所示:
过点P作y轴的平行线PH,分别过点C、Q作CG⊥PH于G,QH⊥PH于H,
∵PQ⊥CP,
∴∠CPQ=∠CGP=∠PHQ=90°,
∴∠CPG+∠PCG=∠CPG+∠QPH=90°,
∴∠PCG=∠QPH,
∴△PCG∽△QPH,
∴,
∵,
∴,
设点P(n,﹣n2+2n+3),
由题意可知:抛物线的对称轴为直线x=1,C(0,3),
∴QH=|n﹣1|,PG=|﹣n2+2n|,
∴,
当时,解得:,
当时,解得:
综上:点P的横坐标为或或或.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习二次函数中线段最值问题
1.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于C(0,﹣4)点,点A的坐标为(﹣1,0).
(1)求抛物线的解析式及B点坐标;
(2)求△ABC的面积;
(3)点P是直线BC下方抛物线上一动点,过点P作y轴平行线交直线BC于点Q,求线段PQ的最大值及此时点P的坐标.
2.平面直角坐标系中,点O是坐标原点,抛物线与y轴交于A(0,﹣3),与x轴交于B、C两点(C在B的右侧),顶点坐标为D(2,1).
(1)求抛物线解析式;
(2)点E是抛物线上一动点,且位于直线AC的上方,过点E作AC的垂线交AC于点F,求EF长度的最大值;
3.如图,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,点M是x轴上方抛物线上一点,作MN⊥BC于点N,求线段MN的最大值;
(3)如图2,点E是第一象限内一点,连接AE交y轴于点D,AE的延长线交抛物线于点P,点F在线段CD上,且CF=OD,连接FA,FE,BE,BP,若S△AFE=S△ABE,求△PAB的面积.
4.如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点P(4,2),对称轴为y轴.A,B是抛物线上两点.
(1)求抛物线的解析式;
(2)若直线AB的解析式为y=kx﹣4k﹣3,且△PAB的面积为35,求k的值;
(3)如图(2),若∠APB=90°,PC⊥AB于点C,求PC的最大值.
5.如图,抛物线y=ax2+bx+c交x轴于点A(3,0)和B(﹣1,0),交y轴于点C(0,3).
(1)求抛物线的表达式;
(2)M是直线AC上方抛物线上一动点,连接OM交AC于点N,当的值最大时,求点M的坐标;
6.如图,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)若P是第二象限的抛物线上的一个动点(不与D重合),过点P作PE⊥x轴交AC于点E,求线段PE长度的最大值;
7.【问题背景】
如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,OA=OC=3,连接AC.
【知识技能】
(1)求此抛物线的解析式.
【构建联系】
(2)在AC下方的抛物线上有一点N,过点N作ND∥y轴,交AC于点M,交x轴于点D,当点N的坐标为多少时,线段MN的长度最大?最大是多少?
8.如图1为某新建住宅小区修建的一个横断面为抛物线的拱形大门,点Q为顶点,其高为5米,宽OP为10米.以点O为原点,OP所在直线为x轴建立直角坐标系.
(1)求出该抛物线的函数表达式;
(2)如图2,小区物业计划在拱形大门处安装一个矩形“光带”ABCD,使点A,D在抛物线上,点B,C在OP上,求出所需的三根“光带”AB,AD,DC的长度之和的最大值.
9.如图,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A、B、C三点的坐标;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;
10.综合与探究
如图,抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(﹣4,0),B(1,0)两点,与y轴交于C点.点D与点C关于x轴对称,直线AD交抛物线于另一点E.
(1)求抛物线的函数表达式,并直接写出直线AD的函数表达式.
(2)点P是直线AE下方抛物线上的一点,过点P作直线AE的垂线,垂足为F.设点P的横坐标为m,试探究当m为何值时,线段PF最大?请求出PF的最大值.
11.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
12.已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
13.如图,抛物线y=x2+bx+c经过A(﹣1,0)、B(4,5)两点,点E是线段AB上一动点,过点E作x轴的垂线,交抛物线于点F.
(1)求抛物线的解析式;
(2)求线段EF的最大值;
14.如图1,在平面直角坐标系中,直线y=x+4与抛物线(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
(1)求该抛物线的解析式;
(2)若点M是抛物线对称轴上的一个动点,当MC+MB的值最小时,求点M的坐标;
(3)P是抛物线上一动点(不与点A、B重合),如图2,若点P在直线AB上方,连接OP交AB于点D,求的最大值.
15.如图,抛物线与x轴相交于A(﹣3,0),B(1,0)两点,且经过点(2,5),点C为抛物线与y轴的交点.
(1)求抛物线的解析式和点C的坐标;
(2)若点P为抛物线图象上的一点,S△POC=4S△BOC,求P点的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
16.综合与探究
如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(2,0),B(0,2),连接AB,P(m,n)为抛物线AB部分上一动点(可与A,B两点重合),过点P作PN⊥x轴交直线AB于点M,交x轴于点N.
(1)求抛物线和直线AB的解析式.
(2)①求线段PM的最大值.
②连接OM,当△OBM为等腰三角形时,求m的值.
17.已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)直接写出A,B,C三点的坐标;
(2)如图1,点P为直线BC下方抛物线上一点,PD⊥BC于点D,求PD的最大值;
(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x﹣9上,求证:直线MN必经过一个定点,并求该定点坐标.
18.已知抛物线y=ax2x﹣6与x轴交于A(t,0),B(8,0)两点,与y轴交于点C,直线y=kx﹣6经过点B,点P在抛物线上,设点P的横坐标为m.
(1)填空:a= ,k= ,t= ;
(2)如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;
(3)如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求CQPQ的最大值.
19.如图,抛物线y=x2+bx﹣5与x轴交于A,B两点(点A在点B的左侧)且B(5,0),抛物线与y轴交于点C,点D为第二象限抛物线上一点,且点D的横坐标为﹣2.
(1)求抛物线的表达式.
(2)若P是y轴上一动点,当PA+PD值最小时,求点P的坐标.
(3)点M为抛物线上一动点,且横坐标为m(0<m<2),过点M作MQ∥y轴交直线BC于点Q,过点M作MN∥x轴,交抛物线于点N,求MQ+MN的最大值.
20.如图,抛物线y=ax2+bx+3交x轴于点A(3,0)和B(﹣1,0),交y轴于点C.
(1)求抛物线的表达式;
(2)D是直线AC上方抛物线上一动点,连接OD交AC于点N,当的值最大时,求点D的坐标;
参考答案
1.【解答】解:(1)把(0,﹣4),(﹣1,0),代入y=x2+bx+c得:
,
解得,
∴抛物线的表达式为y=x2﹣3x﹣4,
令x2﹣3x﹣4=0,则x=﹣1或4,
∴B(4,0);
(2)∵A(﹣1,0),B(4,0),C(0,﹣4),
∴AB=5,OC=4,
;
(3)设直线BC的解析式为yBC=kx﹣4,
∵B(4,0),
∴0=4k﹣4,
解得k=1,
∴直线BC的解析式为yBC=x﹣4,
设P(x,x2﹣3x﹣4),0<x<4,
∵PQ∥y轴,
∴Q(x,x﹣4),
∴PQ=x﹣4﹣(x2﹣3x﹣4)=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,PQmax=4,此时P(2,﹣6),
∴线段PQ的最大值是4,此时点P的坐标为(2,﹣6).
2.【解答】解:(1)∵顶点坐标为D(2,1),
设二次函数的顶点式为y=a(x﹣2)2+1,
∵抛物线与y轴交于A(0,﹣3),
∴a(0﹣2)2+1=﹣3,
解得,a=﹣1.
∴二次函数的解析式为y=﹣x2+4x﹣3;
(2)由题意,由(1)得,抛物线解析式为y=﹣x2+4x﹣3=﹣(x﹣2)2+1.
∴顶点D(2,1).
令y=0,
∴x2﹣4x+3=0.
∴x=1或3.
∴抛物线与x轴的交点B(1,0),C(3,0).
由A(0,﹣3),C(3,0)得,直线AC为y=x﹣3.
由题意,当平行于AC的直线l与抛物线相切时,EF最大.
可设直线l为y=x+m,由抛物线为y=﹣x2+4x﹣3,
∴此时方程为x+m=﹣x2+4x﹣3,
则Δ=9﹣4(3+m)=0.
∴m.
∴l为y=x,又AC为y=x﹣3,
∴(﹣3).
∵直线l与y轴夹角45°,
∴EF的最大值为.
3.【解答】解:(1)物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),将点A,点B的坐标代入得:
,
解得:,
∴抛物线的表达式为;
(2)由B(6,0),C(0,6)解得直线BC的解析式为y=﹣x+6,
过点M作MQ∥y轴交BC于点Q,如图1,
设,Q(m,﹣m+6),
,
∵∠MQN=∠OCB=45°,MN⊥BC,
∴,
∴,
∴当m=3时,MN最大,最大值是;
(3)过F作FG⊥AP于点G,过B作BH⊥AP于点H,过B作BK∥y轴交AP的延长线于点K,如图2,
∵S△AFE=S△ABE,
∴FG=BH,
又∵∠FDG=∠BKH,∠FGD=∠BHK=90°,
∴△FDG≌△BKH(AAS),
∴FD=BK,
∵,
且CF=OD,
∴OD:DF:CF=1:4:1,
∴,
∴D(0,1),
∴直线AD的解析式为,
∵,
∴,
解得x=5或﹣2(舍去),
∴,
∴△PAB的面积,
故△PAB的面积为14.
4.【解答】解:(1)∵抛物线y=ax2+bx+6经过点P(4,2),对称轴为y轴,
∴,
解得,
∴抛物线的解析式为yx2+6;
(2)∵y=kx﹣4k﹣3=k(x﹣4)﹣3,
∴直线AB过定点D(4,﹣3).
如图,连结PD,
∵P(4,2),D(4,﹣3),
∴PD∥y轴,PD=5,
∴S△ABP|xB﹣xA|=35,
∴|xB﹣xA|=14,
由kx﹣4k﹣3x2+6,
整理得x2+4kx﹣16k﹣36=0,
由根与系数的关系得xB+xA=﹣4k,xBxA=﹣16k﹣36,
∴|xB﹣xA|2=(xB+xλ)2﹣4xBxA=142,
∴4k2+16k﹣13=0,
解得k=﹣2或k=﹣2;
∴k的值为﹣2或﹣2;
(3)设A(m,m2+6),B(n,n2+6),直线AB解析式为y=tx+b',
由得x2+tx+b'﹣6=0,
由根与系数的关系得m+n=﹣4t,mn=4b'﹣24,
如图,过点P作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足为E、F,
∴∠E=90°,∠F=90°,
∴∠APE+∠PAE=90°,∠E=∠F,
∵∠APB=90°,
∴∠APE+∠BPF=90°,
∴∠PAE=∠BPF,
∴△PAE∽△BPF,
∴,
∴,
整理变形可得mn+4(m+n)+32=0,
又∵m+n=﹣4t,mn=4b'﹣24,
∴b'=4t﹣2,
∴直线AB的解析式为y=tx+4t﹣2=t(x+4)﹣2,
∴直线AB经过定点C(﹣4,﹣2),
∵P(4,2),
∴PC的最大值为4.
5.【解答】解:(1)抛物线y=ax2+bx+c交x轴于点A(3,0)和B(﹣1,0),交y轴于点C(0,3).将点A、点B、点C的坐标代入得:
,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3.
(2)如图1,过点M作MH∥y轴,交AC于点H,
设直线AC的解析式为y=kx+t,将点A、点C的坐标代入得:
,
解得:,
∴直线AC的解析式为y=﹣x+3,
设M(m,﹣m2+2m+3),则H(m,﹣m+3),
∴MH=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∵MH∥y轴,
∴△MHN∽△OCN,
∴,
∴当时,有最大值,
此时,
∴点M的坐标为.
6.【解答】解:(1)抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D,
令y=0,得:﹣x2﹣2x+3=0,
解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
令x=0,得:y=3,
∴C(0,3),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴D(﹣1,4);
(2)P是第二象限的抛物线上的一个动点(不与D重合),PE⊥x轴交AC于点E,如图1,
设直线AC的解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得,
∴y=x+3,
设P(p,﹣p2﹣2p+3)(﹣3<p<0),则E(p,p+3),
∴PE=﹣p2﹣2p+3﹣(p+3)
=﹣p2﹣3p
,
∴当时,PE有最大值为;
7.【解答】解:(1)∵OA=OC=3,
∴A(﹣3,0),C(0,﹣3),
把A(﹣3,0),C(0,﹣3)代入y=x2+bx+c,得,
,
解得,,
∴此抛物线的解析式为y=x2+2x﹣3;
(2)设直线AC的解析式为y=kx+b,
把把A(﹣3,0),C(0,﹣3)代入y=kx+b,得,
,
解得,
∴直线AC的解析式为y=﹣x﹣3;
设点N的坐标为(x,x2+2x﹣3),则点M(x,﹣x﹣3),
∴DN=﹣(x2+2x﹣3)=﹣x2﹣2x+3,DM=﹣(﹣x﹣3)=x+3,
∴,
∵﹣1<0,
∴MN有最大值,最大值为,
当x时,y=x2+2x﹣3,
∴点N的坐标为;
8.【解答】解:(1)由题意可设这条抛物线的函数解析式为y=a(x﹣5)2+5,
∵抛物线过O(0,0),
∴25a+5=0,
解得a,
∴这条抛物线的函数解析式为y(x﹣5)2+5;
(2)设点A的坐标为(m,m2+2m),
则OB=m,AB=DC2m,
根据抛物线的轴对称,可得:OB=m=CP,BC=10﹣2m,AD=10﹣2m,
令L=AB+AD+DC
2m+10﹣2m
2m+10
,
∵0,开口向下,
∴当m时,最大值为,
∴当OB米时,三根“光带”长度之和的最大值为米.
9.【解答】解:(1)对于y=﹣x2+2x+3,令x=0,则y=3,
∴C(0,3),
令y=0,则y﹣x2+2x+3=0,解得:x1=3,x2=﹣1,
∴A(﹣1,0),
∴B(3,0);
(2)设BC的表达式为y=kx+b,则,解得,
∴直线BC的表达式为y=﹣x+3,
设点P的坐标为(t,﹣t+3),则点M的坐标为(t,﹣t2+2t+3),
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t=﹣(t)2,
t时,PM最大,
此时点M坐标(,);
10.【解答】解:(1)将A(﹣4,0),B(1,0)代入y=ax2+bx﹣2(a≠0)得:,
解得:,
∴二次函数的解析式为:;
在中,当x=0时,y=﹣2,
∴C(0,﹣2),
∵点D与点C关于x轴对称,
∴D(0,2),
设直线AD的表达式为y=kx+b1,
将D(0,2),A(﹣4,0)代入解析式得:,
解得:,
∴直线AD的表达式为;
(2)存在,理由如下:
如图,过点P作y轴的平行线交AD于G,
∴∠AGP=∠ADC,
∵A(﹣4,0),D(0,2),
∴OA=4,OD=2,
∴,
∴,
∴在Rt△PFG中,,
∴,
∴当GP取得最大值时,PF取得最大值,
设点,则,
∴,
∵,
∴当m=﹣1时,GP取得最大值为,
∴PF的最大值为;
11.【解答】解:(1)∵抛物线过A、C两点,
∴代入抛物线解析式可得:,解得:,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得,解得,
∴直线BC解析式为y=﹣x+3;
(2)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,﹣m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m)2,
∴当m时,MN有最大值,MN的最大值为;
12.【解答】解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得 ;
故直线BC的解析式:y=﹣x+3.
已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
13.【解答】解:(1)把A(﹣1,0)、B(4,5)代入y=x2+bx+c,得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)设F(x,x2﹣2x﹣3)(﹣1<x<4),
设直线AB的解析式为y=kx+b,代入点A(﹣1,0)、B(4,5),得:
,
解得:,
∴直线AB的解析式为y=x+1,
∵EF∥y轴,
∴E(x,x+1),
∴EF=x+1﹣(x2﹣2x﹣3)=﹣x2+3x+4,
当x时,EF取得最大值为;
14.【解答】解:(1)∵直线y=x+4与坐标轴交于A、B两点,
当x=0时,y=4,当y=0时,x=﹣4,
∴A(﹣4,0),B(0,4),
将A、B代入抛物线,
得,
解得,
∴抛物线的解析式为y.
答:抛物线的解析式为y.
(2)∵抛物线的解析式为y.
∴当y=0时,解得x1=﹣4,x2=2,
∴抛物线的对称轴为直线x,
∵A(﹣4,0),C(2,0)关于x=﹣1对称,
如图,连接AB交对称轴于点M,
∴MB+MC=MB+MA=AB,
此时MC+MB取得最小值.
∴当x=﹣1时,y=﹣1+4=3,
∴M(﹣1,3).
答:点M的坐标为(﹣1,3).
(3)如图,过点P作PE∥OB交AB于点E,
则△PDE∽△ODB,
∴,
设点P(m,)(﹣4<m<0),
∴E(m,m+4),
∴,
∴,
∴当m时有最大值,
∴的最大值为.
答:的最大值的最大值为.
15.【解答】解:(1)∵抛物线与x轴相交于A(﹣3,0),B(1,0)两点,且经过点(2,5),
∴,
解得.
所以抛物线的解析式为:y=x2+2x﹣3;
(2)二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴3×|x|=43×1,
∴|x|=4,x=4或﹣4.
∴当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
(3)设直线AC的解析式为y=kx﹣3,将A(﹣3,0)代入,
得0=﹣3k﹣3,
解得k=﹣1.
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x)2,
∴当x时,QD有最大值.
16.【解答】解:(1)∵抛物线经过点B(0,2),
∴y=﹣x2+bx+2.
将点A(2,0)代入,得0=﹣22+2b+2,
解得:b=1,
抛物线的解析式为y=﹣x2+x+2.
设直线AB的解析式为y=kx+2,
将点A(2,0)代入,得0=2k+2,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+2.
(2)①将P(m,n)代入y=﹣x2+x+2中,得n=﹣m2+m+2.
将x=m代入y=﹣x+2中,得y=﹣m+2.
∴PM=n﹣y=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m=﹣(m﹣1)2+1,
即PM的最大值为1.
②∵点M在直线AB上,且点P(m,n),
∴点M的坐标为(m,﹣m+2).
∵点B(0,2),
∴OB=2,
∴BM2=(m﹣0)2+(﹣m+2﹣2)2=2m2,
OM2=m2+(﹣m+2)2=2m2﹣4m+4.
当△OBM为等腰三角形时,
(ⅰ)若BM=OM,则BM2=OM2,
即2m2=2m2﹣4m+4,解得m=1.
(ⅱ)若BM=OB,则BM2=OB2,
即2m2=4,
解得:或(舍去).
(ⅲ)若OM=OB,则OM2=OB2,
即2m2﹣4m+4=4,
解得:m=2或m=0(舍去).
综上所述,m=1或或m=2.
17.【解答】(1)解:对于y=x2﹣2x﹣3,令y=0,则0=x2﹣2x﹣3,
∴x1=﹣1,x2=3,
∴点A(﹣1,0),点B(3,0),
令x=0,则y=﹣3,
∴点C(0,﹣3);
(2)解:过点P作PE⊥x轴于E,交BC于点F,如图1:
设直线BC的解析式为y=kx+b,
将点B(3,0),C(0,﹣3)代入y=kx+b得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
设P(x,x2﹣2x﹣3),则F(x,x﹣3),
∴PF=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∵PE⊥x轴,
∴PE∥y轴,
∴∠PFD=∠BCO,
∵∠PDF=∠BOC=90°,
∴△PDF∽△BCO,
∴,
∵B(3,0),C(0,﹣3),
∴OB=3,OC=3,
∴BC=3,
∴,
∴PDx2x,
∴当x时,PD最大为;
(3)证明:如图2,设点M(xM,yM),N(xN,yN),
直线MN:y=k′x+b′,直线CM:y=k1x+b1,直线BN:y=k2x+b2,
将点C(0,﹣3)代入直线CM的解析式得:b1=﹣3,
将点B(3,0)代入直线BN的解析式得:b2=﹣3k2,
联立直线MN与抛物线的解析式得:,
整理得:x2﹣(k′+2)x﹣b′﹣3=0,
则xM+xN=k′+2,xM xN=﹣b′﹣3,
同理:xM+xC=k1+2,xN+xB=k2+2,
∵xC=0,xB=3,
∴xM=k1+2,xN=k2﹣1,
∴k′=xM+xN﹣2=k1+2+k2﹣1﹣2=k1+k2﹣1,
b′=﹣xM xN﹣3=﹣(k1+2)(k2﹣1)﹣3=﹣k1k2﹣2k2+k1+2﹣3=﹣k1k2﹣2k2+k1﹣1,
联立直线CM与直线BN的解析式得:,
解得:,
∵直线BN与直线CM的交点始终在直线y=2x﹣9上,
∴29,
化简得:k1k2=3k1﹣2,
∴b′=﹣k1k2﹣2k2+k1﹣1=﹣3k1+2﹣2k2+k1﹣1=﹣2k1﹣2k2+1=﹣2(k1+k2)+1=﹣2(k′+1)+1=﹣2k′﹣1,
∴直线MN:y=k′x﹣2k′﹣1=k′(x﹣2)﹣1,
∴不论k′为何值,均有x=2时,y=﹣1,
即:直线MN恒过定点P(2,﹣1).
18.【解答】解:(1)将B(8,0)代入y=ax2x﹣6,
∴64a+22﹣6=0,
∴a,
∴yx2x﹣6,
当y=0时,t2t﹣6=0,
解得t=3或t=8(舍),
∴t=3,
∵B(8,0)在直线y=kx﹣6上,
∴8k﹣6=0,
解得k;
故答案为:;;3;
(2)作PM⊥x轴交于M,
∵P点横坐标为m,
∴P(m,m2m﹣6),
∴PMm2m+6,AM=m﹣3,
在Rt△COA和Rt△AMP中,
∵∠OAC+∠PAM=90°,∠APM+∠PAM=90°,
∴∠OAC=∠APM,
∴△COA∽△AMP,
∴,即OA MA=CO PM,
3(m﹣3)=6(m2m+6),
解得m=3(舍)或m=10,
∴P(10,);
(3)作PN⊥x轴交BC于N,过点N作NE⊥y轴交于E,
∴PNm2m﹣6﹣(m﹣6)m2+2m,
∵PN⊥x轴,
∴PN∥OC,
∴∠PNQ=∠OCB,
∴Rt△PQN∽Rt△BOC,
∴,
∵OB=8,OC=6,BC=10,
∴QNPN,PQPN,
由△CNE∽△CBO,
∴CNENm,
∴CQPQ=CN+NQPQ=CN+PN,
∴CQPQmm2+2mm2m(m)2,
当m时,CQPQ的最大值是.
19.【解答】解:(1)把(5,0)代入y=x2+bx﹣5中,
0=25+5b﹣5,
得b=﹣4,
∴y=x2﹣4x﹣5;
(2)在y=x2﹣4x﹣5中,
当x=﹣2时:y=7,
∴点D的坐标为(﹣2,7),
当y=0时:x1=﹣1,x2=5,
∴点A的坐标为(﹣1,0),
作点A关于y轴的对称点E,
∵A点坐标为(﹣1,0),
∴E点坐标为(1,0),
连接DE交y轴于点P,
此时PA+PD最小,
设直线DE为y=kx+b,
∴
解得:,
∴直线DE的表达式为
∴点P的坐标为;
(3)如图:
在y=x2﹣4x﹣5中,
当x=0时:y=﹣5,
∴点C的坐标为(0,﹣5),
设直线BC解析式为y=k1x+b2,则
解得,
∴直线BC表达式:y=x﹣5,
设M点坐标为(m,m2﹣4m﹣5),
Q点坐标(m,m﹣5),
∴MQ=m﹣5﹣m2+4m+5=﹣m2+5m,
∵M和N关于对称轴对称,对称轴为直线,
∴MN=2(2﹣m)=4﹣2m,
∴MN+MQ=4﹣2m+(﹣m2+5m)
=﹣m2+3m+4
,
∵﹣1<0,
∴当时MN+MQ有最大值.
20.【解答】解:(1)把点A(3,0)和B(﹣1,0)代入得:,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)过点D作DH∥y轴,交AC于点H,如图所示:
设D(m,﹣m2+2m+3),直线AC的解析式为y=kx+b,
由(1)可得:C(0,3),
∴,解得:,
∴直线AC的解析式为y=﹣x+3,
∴H(m,﹣m+3),
∴DH=﹣m2+3m,
∵DH∥y轴,
∴△OCN∽△DHN,
∴,
∵,
∴当时,的值最大,
∴;
(3)由题意可得如图所示:
过点P作y轴的平行线PH,分别过点C、Q作CG⊥PH于G,QH⊥PH于H,
∵PQ⊥CP,
∴∠CPQ=∠CGP=∠PHQ=90°,
∴∠CPG+∠PCG=∠CPG+∠QPH=90°,
∴∠PCG=∠QPH,
∴△PCG∽△QPH,
∴,
∵,
∴,
设点P(n,﹣n2+2n+3),
由题意可知:抛物线的对称轴为直线x=1,C(0,3),
∴QH=|n﹣1|,PG=|﹣n2+2n|,
∴,
当时,解得:,
当时,解得:
综上:点P的横坐标为或或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
