选择必修第三册 第六章 6.2.1 排列 课件(共22张PPT)
文档属性
| 名称 | 选择必修第三册 第六章 6.2.1 排列 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 959.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 11:28:42 | ||
图片预览







文档简介
(共22张PPT)
选择必修三
第六章 计数原理
6.2 排列与组合
6.2.1 排列
教学目标
学习目标 数学素养
1.理解并掌握排列的概念. 1.归纳的数学素养.
2.能应用排列知识解决简单的实际问题. 2.数学建模素养和数学运算素养.
温故知新
1.分类加法计数原理:
完成一件事,如果有n类不同的方案,而且第一类方案中有m1种不同的方法,第二类方案中有m2种不同的方法……第n类方案中有mn种不同的方法,那么完成这件事共有
N=m1+m2+…+mn
种不同的方法.
2.分步乘法计数原理:
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有
N=m1×m2×…×mn.
种不同的方法.
分类加法计数原理使用前提:
各类方案中的方法互不相同且都能独立完成这件事情.
分步乘法计数原理使用前提:
各步中每种方法不能独立完成这件事.
温故知新
两个原理的区别与联系:
分类加法计数原理 分步乘法计数原理
相同点 不同点
注意点
用来计算“完成一件事”的不同方法种数
分类完成,类类相加
分步完成,步步相乘
各类中每种方法都能独立完成这件事
每步依次完成才算完成这件事(各步中每种方法不能独立完成这件事)
类类独立,不重不漏
步步依存,步骤完整
知新探究
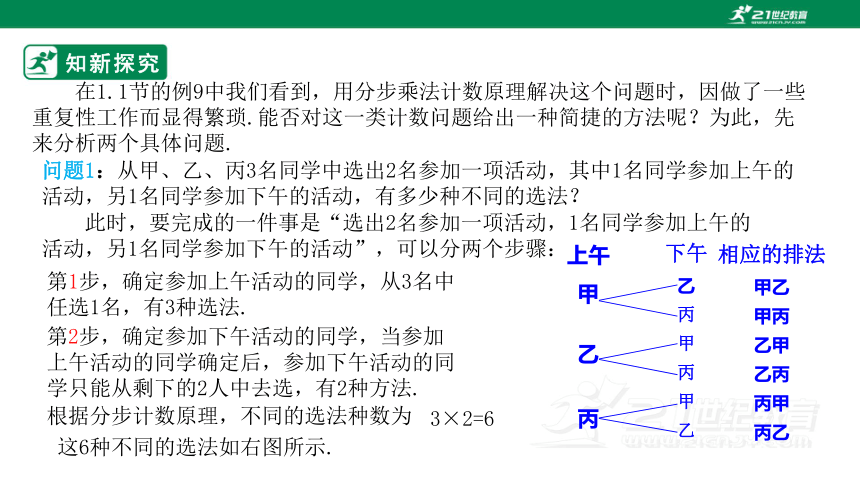
在1.1节的例9中我们看到,用分步乘法计数原理解决这个问题时,因做了一些重复性工作而显得繁琐.能否对这一类计数问题给出一种简捷的方法呢?为此,先来分析两个具体问题.
此时,要完成的一件事是“选出2名参加一项活动,1名同学参加上午的活动,另1名同学参加下午的活动”,可以分两个步骤:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
第1步,确定参加上午活动的同学,从3名中任选1名,有3种选法.
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种方法.
下午
乙
丙
甲
丙
甲
乙
相应的排法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
上午甲
乙
丙
根据分步计数原理,不同的选法种数为
3×2=6
这6种不同的选法如右图所示.
知新探究
如果把上面问题中被取的对象叫做元素,那么问题1可以叙述为:
所有不同的排列是
ab, ac, ba, bc, ca, cb
3×2=6.
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
不同的排列方法种数为
问题1中的“顺序”是什么?
问题1中的“顺序”是上午、下午.
知新探究
显然,从4个数字中,每次取出3个,按“百万、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.
可以分三个步骤来解决这个问题:
4×3×2=24.
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种选法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种选法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位上的数字只能从余下的2个数字中去取,有2种选法.
根据分步乘法计数原理,从1,2,3,4这4个数中,每次取出3个排成一个三位数,按“百万、十位、个位”的顺序排成一列,不同的排法种数为
知新探究
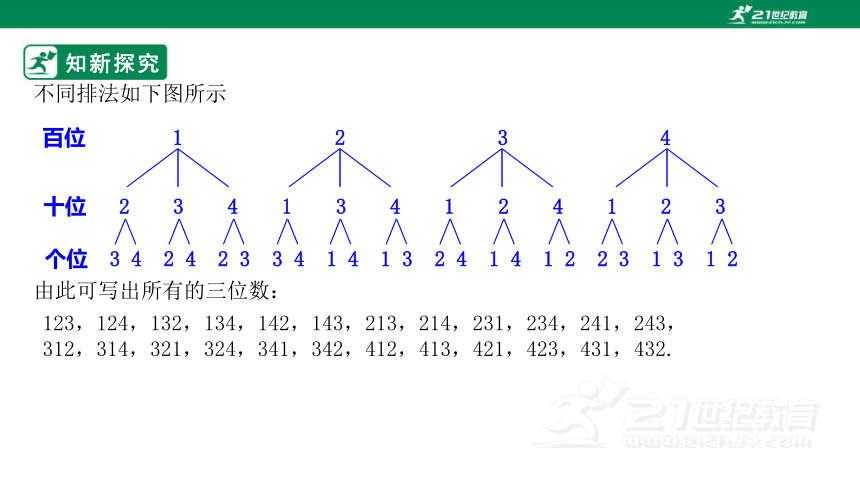
由此可写出所有的三位数:
不同排法如下图所示
百位 1 2 3 4
十位 2 3 4 1 3 4 1 2 4 1 2 3
个位 3 4 2 4 2 3 3 4 1 4 1 3 2 4 1 4 1 2 2 3 1 3 1 2
123,124,132,134,142,143,213,214,231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
知新探究
同样,问题2可以归结为:
abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb.
从4个不同的元素a,b,c,d 中任取3个,然后按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
不同的排列方法种数为
4×3×2=24.
问题2中的“顺序”是什么?
问题2中的“顺序”是百位、十位、个位.
知新探究
问题1和问题2都是研究从一些不同元素中取出部分元素,并按一定的顺序排成一列的方法数.
上述问题1,2的共同特点是什么?你能将它们的推广到一般情形吗?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
知新探究
1.元素不能重复. n个中不能重复,m个中也不能重复.这里即没有重复的元素,又没有重复抽取同一元素的情况.
1、排列:
一般地,从 n 个不同中取出 m 个元素(m ≤ n),按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列(arrangement).
注意:
2.“按一定顺序”就是与位置有关.排列包括两个方面:
3.两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同.
4.m<n时的排列叫选排列,m=n时的排列叫全排列.
取出元素→按一定顺序排列
5.为了使写出的所有排列情况既不重复也不遗漏, 最好采用“树状图”.
知新探究
【例1】下列问题中哪些是排列问题?
⑴北京、上海、天津3个民航站之间的直达航线的飞机票的价格(假设往返的票价相同);
⑵选2个小组分别去植树和打扫卫生;
⑶选2个小组去植树;
⑷选10个人组成一个学习小组;
⑸选3个人分别担任班长、学习委员、生活委员.
解:
⑴中票价只有3种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
⑵植树和打扫卫生是不同的,存在顺序问题,属于排列问题.
⑸中每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
⑶,⑷不存在顺序问题,不属于排列问题.
初试身手
1.(多选题)下列问题中是排列问题的是( )
A.从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组
B.从甲、乙、丙三名同学中选出两名同学参加一项活动
C.从a,b,c,d四个字母中取出2个字母
D.从2,3,5,7,11中任取两个数相除.
A是排列问题,因为两名同学参加的学习小组与顺序有关;
B不是排列问题,因为两名同学参加的活动与顺序无关;
故选AD.
解:
C不是排列问题,因为取出的两个字母与顺序无关;
D是排列问题,因为取出的两个数字还需要按“分子,分母”的顺序排成一列.
AD
知新探究
【例2】某省中学生足球预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的1场比赛,可以看作是该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.
解:
可以从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队.
按分步乘法计数原理,每组进行的比赛场数为
6×5=30.
注意:本题中比赛的2支队的顺序为“主队、客队”.
初试身手
2.⑴从8名学生干部中选2名做正、副组长,共有多少种选法?
⑵有10个车站,共需要多少种车票?
⑴从8名学生干部中先选1名担任班长,然后从剩下的7名学生干部中再选1名担任副班长.
⑵先从10个车站中选1个作为始站,再从剩下的9个站中选1个站作为终站,构成一个车票.
8×7=56.
解:
按分步乘法计数原理,共有不同的选法种数为
按分步乘法计数原理,共有不同的车票种数为
10×9=90.
知新探究
【例3】⑴一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
⑵学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
分析:3名同学每人从5盘不同的菜中取1盘菜,可看作是从这5盘菜中任取3盘,放在3个位置(给3名同学)的一个排列;而3名同学从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列.
解:
⑴可以先从这5盘菜中取1盘给同学甲,然后从剩下4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为
5×4×3=60.
⑵可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从从5种菜中选1种,有5种选法; 最后让同学丙从5种菜中选1种,有5种选法. 按分步乘法计数原理,不同的取法种数为
5×5×5=125.
初试身手
3.⑴从0,1,2,3,4,5这6个数字中任取3个不同数字,可以构成多少个三位数?
⑵由0,1,2,3,4,5这6个数字可以构成多少个三位数?
⑴取3个不同数字按“百位十位个位”顺序组成三位数是一个排列.分3步:
解:
第1步,从1,2,3,4,5这5个数字取1个数填在“百位”;第2步从0,1,2,3,4,5这6个数字中取1个填在“十位”;第3步从0,1,2,3,4,5这6个数字中取1个填在“个位”.
根据分步乘法计数原理,可构成的三位数的个数为
第1步,从1,2,3,4,5这5个数字取1个数填在“百位”;第2步从剩余的5个数中取1个填在“十位”;第3步从剩余的4个数中取1个填在“个位”.
根据分步乘法计数原理,可构成的三位数的个数为
5×5×4=100.
⑵由于“百位十位个位”三位数的数字可以重复,分3步:
5×6×6=180.
课堂小结
1.排列的定义
2.排列问题的判断方法:
⑴元素的无重复性;
⑵元素的有序性.
一般地,从 n 个不同中取出 m 个元素(m ≤ n),按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列(arrangement).
判断关键是看选出的元素有没有顺序要求.
作业布置
作业:
P16-17 练习 第1,2,3题
P26 习题6.2 第3,4题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修三
第六章 计数原理
6.2 排列与组合
6.2.1 排列
教学目标
学习目标 数学素养
1.理解并掌握排列的概念. 1.归纳的数学素养.
2.能应用排列知识解决简单的实际问题. 2.数学建模素养和数学运算素养.
温故知新
1.分类加法计数原理:
完成一件事,如果有n类不同的方案,而且第一类方案中有m1种不同的方法,第二类方案中有m2种不同的方法……第n类方案中有mn种不同的方法,那么完成这件事共有
N=m1+m2+…+mn
种不同的方法.
2.分步乘法计数原理:
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有
N=m1×m2×…×mn.
种不同的方法.
分类加法计数原理使用前提:
各类方案中的方法互不相同且都能独立完成这件事情.
分步乘法计数原理使用前提:
各步中每种方法不能独立完成这件事.
温故知新
两个原理的区别与联系:
分类加法计数原理 分步乘法计数原理
相同点 不同点
注意点
用来计算“完成一件事”的不同方法种数
分类完成,类类相加
分步完成,步步相乘
各类中每种方法都能独立完成这件事
每步依次完成才算完成这件事(各步中每种方法不能独立完成这件事)
类类独立,不重不漏
步步依存,步骤完整
知新探究
在1.1节的例9中我们看到,用分步乘法计数原理解决这个问题时,因做了一些重复性工作而显得繁琐.能否对这一类计数问题给出一种简捷的方法呢?为此,先来分析两个具体问题.
此时,要完成的一件事是“选出2名参加一项活动,1名同学参加上午的活动,另1名同学参加下午的活动”,可以分两个步骤:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
第1步,确定参加上午活动的同学,从3名中任选1名,有3种选法.
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种方法.
下午
乙
丙
甲
丙
甲
乙
相应的排法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
上午甲
乙
丙
根据分步计数原理,不同的选法种数为
3×2=6
这6种不同的选法如右图所示.
知新探究
如果把上面问题中被取的对象叫做元素,那么问题1可以叙述为:
所有不同的排列是
ab, ac, ba, bc, ca, cb
3×2=6.
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
不同的排列方法种数为
问题1中的“顺序”是什么?
问题1中的“顺序”是上午、下午.
知新探究
显然,从4个数字中,每次取出3个,按“百万、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.
可以分三个步骤来解决这个问题:
4×3×2=24.
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种选法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种选法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位上的数字只能从余下的2个数字中去取,有2种选法.
根据分步乘法计数原理,从1,2,3,4这4个数中,每次取出3个排成一个三位数,按“百万、十位、个位”的顺序排成一列,不同的排法种数为
知新探究
由此可写出所有的三位数:
不同排法如下图所示
百位 1 2 3 4
十位 2 3 4 1 3 4 1 2 4 1 2 3
个位 3 4 2 4 2 3 3 4 1 4 1 3 2 4 1 4 1 2 2 3 1 3 1 2
123,124,132,134,142,143,213,214,231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
知新探究
同样,问题2可以归结为:
abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb.
从4个不同的元素a,b,c,d 中任取3个,然后按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
不同的排列方法种数为
4×3×2=24.
问题2中的“顺序”是什么?
问题2中的“顺序”是百位、十位、个位.
知新探究
问题1和问题2都是研究从一些不同元素中取出部分元素,并按一定的顺序排成一列的方法数.
上述问题1,2的共同特点是什么?你能将它们的推广到一般情形吗?
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
知新探究
1.元素不能重复. n个中不能重复,m个中也不能重复.这里即没有重复的元素,又没有重复抽取同一元素的情况.
1、排列:
一般地,从 n 个不同中取出 m 个元素(m ≤ n),按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列(arrangement).
注意:
2.“按一定顺序”就是与位置有关.排列包括两个方面:
3.两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同.
4.m<n时的排列叫选排列,m=n时的排列叫全排列.
取出元素→按一定顺序排列
5.为了使写出的所有排列情况既不重复也不遗漏, 最好采用“树状图”.
知新探究
【例1】下列问题中哪些是排列问题?
⑴北京、上海、天津3个民航站之间的直达航线的飞机票的价格(假设往返的票价相同);
⑵选2个小组分别去植树和打扫卫生;
⑶选2个小组去植树;
⑷选10个人组成一个学习小组;
⑸选3个人分别担任班长、学习委员、生活委员.
解:
⑴中票价只有3种,虽然机票是不同的,但票价是一样的,不存在顺序问题,所以不是排列问题.
⑵植树和打扫卫生是不同的,存在顺序问题,属于排列问题.
⑸中每个人的职务不同,例如甲当班长或当学习委员是不同的,存在顺序问题,属于排列问题.
⑶,⑷不存在顺序问题,不属于排列问题.
初试身手
1.(多选题)下列问题中是排列问题的是( )
A.从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组
B.从甲、乙、丙三名同学中选出两名同学参加一项活动
C.从a,b,c,d四个字母中取出2个字母
D.从2,3,5,7,11中任取两个数相除.
A是排列问题,因为两名同学参加的学习小组与顺序有关;
B不是排列问题,因为两名同学参加的活动与顺序无关;
故选AD.
解:
C不是排列问题,因为取出的两个字母与顺序无关;
D是排列问题,因为取出的两个数字还需要按“分子,分母”的顺序排成一列.
AD
知新探究
【例2】某省中学生足球预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的1场比赛,可以看作是该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.
解:
可以从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队.
按分步乘法计数原理,每组进行的比赛场数为
6×5=30.
注意:本题中比赛的2支队的顺序为“主队、客队”.
初试身手
2.⑴从8名学生干部中选2名做正、副组长,共有多少种选法?
⑵有10个车站,共需要多少种车票?
⑴从8名学生干部中先选1名担任班长,然后从剩下的7名学生干部中再选1名担任副班长.
⑵先从10个车站中选1个作为始站,再从剩下的9个站中选1个站作为终站,构成一个车票.
8×7=56.
解:
按分步乘法计数原理,共有不同的选法种数为
按分步乘法计数原理,共有不同的车票种数为
10×9=90.
知新探究
【例3】⑴一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
⑵学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
分析:3名同学每人从5盘不同的菜中取1盘菜,可看作是从这5盘菜中任取3盘,放在3个位置(给3名同学)的一个排列;而3名同学从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列.
解:
⑴可以先从这5盘菜中取1盘给同学甲,然后从剩下4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为
5×4×3=60.
⑵可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从从5种菜中选1种,有5种选法; 最后让同学丙从5种菜中选1种,有5种选法. 按分步乘法计数原理,不同的取法种数为
5×5×5=125.
初试身手
3.⑴从0,1,2,3,4,5这6个数字中任取3个不同数字,可以构成多少个三位数?
⑵由0,1,2,3,4,5这6个数字可以构成多少个三位数?
⑴取3个不同数字按“百位十位个位”顺序组成三位数是一个排列.分3步:
解:
第1步,从1,2,3,4,5这5个数字取1个数填在“百位”;第2步从0,1,2,3,4,5这6个数字中取1个填在“十位”;第3步从0,1,2,3,4,5这6个数字中取1个填在“个位”.
根据分步乘法计数原理,可构成的三位数的个数为
第1步,从1,2,3,4,5这5个数字取1个数填在“百位”;第2步从剩余的5个数中取1个填在“十位”;第3步从剩余的4个数中取1个填在“个位”.
根据分步乘法计数原理,可构成的三位数的个数为
5×5×4=100.
⑵由于“百位十位个位”三位数的数字可以重复,分3步:
5×6×6=180.
课堂小结
1.排列的定义
2.排列问题的判断方法:
⑴元素的无重复性;
⑵元素的有序性.
一般地,从 n 个不同中取出 m 个元素(m ≤ n),按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列(arrangement).
判断关键是看选出的元素有没有顺序要求.
作业布置
作业:
P16-17 练习 第1,2,3题
P26 习题6.2 第3,4题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
