1.1.1等腰三角形(1)同步练习(无答案)八年级下册数学北师版
文档属性
| 名称 | 1.1.1等腰三角形(1)同步练习(无答案)八年级下册数学北师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 62.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 09:47:24 | ||
图片预览

文档简介
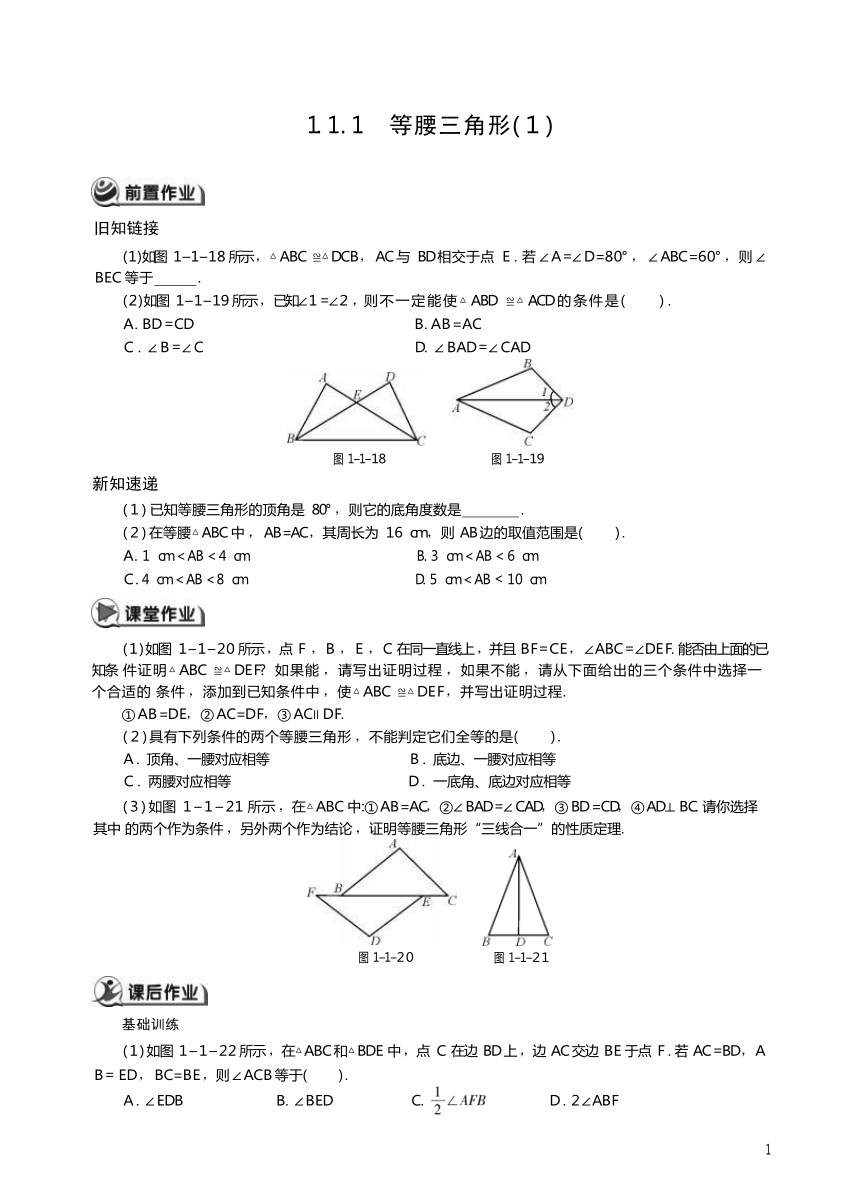
1 . 1 . 1 等腰三角形(1)
旧知链接
(1) 如图 1–1–18 所示 , △ABC ≌△DCB ,AC 与 BD 相交于点 E . 若 ∠A = ∠D =80 ° , ∠ABC =60 ° ,则 ∠BEC 等于 .
(2) 如图 1–1–19 所示 , 已知∠1 = ∠2 ,则不一定能使△ABD ≌△ACD 的条件是( ) .
A . BD =CD B . AB =AC
C . ∠B = ∠C D . ∠BAD = ∠CAD
图 1–1–18 图 1–1–19
新知速递
(1) 已知等腰三角形的顶角是 80 ° ,则它的底角度数是 .
(2) 在等腰△ABC 中 ,AB =AC ,其周长为 16 cm ,则 AB 边的取值范围是( ) .
A . 1 cm < AB < 4 cm B . 3 cm < AB < 6 cm
C . 4 cm < AB < 8 cm D . 5 cm < AB < 10 cm
(1) 如图 1–1–20 所示 ,点 F ,B ,E ,C 在同一直线上 ,并且 BF= CE , ∠ABC = ∠DEF. 能否由上面的已知条 件证明△ABC ≌△DEF 如果能 ,请写出证明过程 ,如果不能 ,请从下面给出的三个条件中选择一个合适的 条件 ,添加到已知条件中 ,使△ABC ≌△DEF ,并写出证明过程.
①AB =DE,②AC=DF,③AC∥DF.
(2) 具有下列条件的两个等腰三角形 ,不能判定它们全等的是( ) .
A . 顶角、一腰对应相等 B . 底边、一腰对应相等
C . 两腰对应相等 D . 一底角、底边对应相等
(3) 如图 1–1–21 所示 ,在△ABC 中:①AB =AC,②∠BAD = ∠CAD,③BD =CD,④AD⊥BC. 请你选择其中 的两个作为条件 ,另外两个作为结论 ,证明等腰三角形“三线合一”的性质定理.
1
图 1–1–20
图 1–1–21
基础训练
(1) 如图 1–1–22 所示 ,在△ABC 和△BDE 中 ,点 C 在边 BD 上 ,边 AC 交边 BE 于点 F. 若 AC =BD ,AB = ED ,BC=BE ,则 ∠ACB 等于( ) .
A . ∠EDB B . ∠BED C . D . 2∠ABF
(2) 如图 1-1-23 所示的图形是由四个完全相同的四边形 OABC 拼成的. 测得 AB =BC , OA = OC , OA ⊥ OC , ∠ABC=36 ° ,则 ∠OAB 的度数是( ) .
A . 116 ° B . 117 ° C . 118 ° D . 119 °
2
图 1-1-22
图 1-1-23
(3) 等腰三角形一边长等于 5 ,一边长等于 6 ,则它的周长为 .
(4) 一个三角形有两边长相等 ,周长为 20 cm ,它的一边长为 6 cm ,则其他的两边长为 .
(5) 如图 1-1-24 所示 , 在△ABC 中 ,AB =AC , 且 D 为 BC 上一点 , CD =AD ,AB =BD , 则 ∠B 的度数为
.
图 1-1-24
拓展提高
(1)若等腰三角形的一边长为 12 cm ,且腰长是底边长的 ,求这个三角形的周长.
(2) 如图 1-1-25 所示 ,D 为△ABC 的边 BC 延长线上一点 ,且 CD = CA ,E 是 AD 的中点 , CF 平分 ∠ACB 交 AB 于点 F. 求证 :CE⊥CF.
(3) 如图 1-1-26 所示 , △ABC 是等腰三角形 ,AB =AC. D ,E 分别是腰AB 及 AC 延长线上的一点 ,且 BD = CE ,连接 DE 交底 BC 于 G. 求证 :GD =GE .
图 1-1-25
图 1-1-26
发散思维
(1) ①如图 1-1-27 ( a) 所示 , 在 Rt △ABC 中 , ∠ACB =90 ° , 点 D , E 在边 AB 上 , 且 AD =AC , BE = BC , 求 ∠DCE 的度数.
②如图 1-1-27( b) 所示 ,在△ABC 中 , ∠ACB =40 ° ,点 D ,E 在直线 AB 上 ,且 AD =AC ,BE =BC ,求 ∠DCE 的度数.
图 1-1-27
(2) 在△ABC 中 , ∠ACB=n ° (0 < n < 180) ,点 D、点 E 在直线AB 上 ,且 AD=AC ,BE=BC ,求 ∠DCE 的度数 ( 直接写出答案 ,用含 n 的式子表示) .
旧知链接
(1) 如图 1–1–18 所示 , △ABC ≌△DCB ,AC 与 BD 相交于点 E . 若 ∠A = ∠D =80 ° , ∠ABC =60 ° ,则 ∠BEC 等于 .
(2) 如图 1–1–19 所示 , 已知∠1 = ∠2 ,则不一定能使△ABD ≌△ACD 的条件是( ) .
A . BD =CD B . AB =AC
C . ∠B = ∠C D . ∠BAD = ∠CAD
图 1–1–18 图 1–1–19
新知速递
(1) 已知等腰三角形的顶角是 80 ° ,则它的底角度数是 .
(2) 在等腰△ABC 中 ,AB =AC ,其周长为 16 cm ,则 AB 边的取值范围是( ) .
A . 1 cm < AB < 4 cm B . 3 cm < AB < 6 cm
C . 4 cm < AB < 8 cm D . 5 cm < AB < 10 cm
(1) 如图 1–1–20 所示 ,点 F ,B ,E ,C 在同一直线上 ,并且 BF= CE , ∠ABC = ∠DEF. 能否由上面的已知条 件证明△ABC ≌△DEF 如果能 ,请写出证明过程 ,如果不能 ,请从下面给出的三个条件中选择一个合适的 条件 ,添加到已知条件中 ,使△ABC ≌△DEF ,并写出证明过程.
①AB =DE,②AC=DF,③AC∥DF.
(2) 具有下列条件的两个等腰三角形 ,不能判定它们全等的是( ) .
A . 顶角、一腰对应相等 B . 底边、一腰对应相等
C . 两腰对应相等 D . 一底角、底边对应相等
(3) 如图 1–1–21 所示 ,在△ABC 中:①AB =AC,②∠BAD = ∠CAD,③BD =CD,④AD⊥BC. 请你选择其中 的两个作为条件 ,另外两个作为结论 ,证明等腰三角形“三线合一”的性质定理.
1
图 1–1–20
图 1–1–21
基础训练
(1) 如图 1–1–22 所示 ,在△ABC 和△BDE 中 ,点 C 在边 BD 上 ,边 AC 交边 BE 于点 F. 若 AC =BD ,AB = ED ,BC=BE ,则 ∠ACB 等于( ) .
A . ∠EDB B . ∠BED C . D . 2∠ABF
(2) 如图 1-1-23 所示的图形是由四个完全相同的四边形 OABC 拼成的. 测得 AB =BC , OA = OC , OA ⊥ OC , ∠ABC=36 ° ,则 ∠OAB 的度数是( ) .
A . 116 ° B . 117 ° C . 118 ° D . 119 °
2
图 1-1-22
图 1-1-23
(3) 等腰三角形一边长等于 5 ,一边长等于 6 ,则它的周长为 .
(4) 一个三角形有两边长相等 ,周长为 20 cm ,它的一边长为 6 cm ,则其他的两边长为 .
(5) 如图 1-1-24 所示 , 在△ABC 中 ,AB =AC , 且 D 为 BC 上一点 , CD =AD ,AB =BD , 则 ∠B 的度数为
.
图 1-1-24
拓展提高
(1)若等腰三角形的一边长为 12 cm ,且腰长是底边长的 ,求这个三角形的周长.
(2) 如图 1-1-25 所示 ,D 为△ABC 的边 BC 延长线上一点 ,且 CD = CA ,E 是 AD 的中点 , CF 平分 ∠ACB 交 AB 于点 F. 求证 :CE⊥CF.
(3) 如图 1-1-26 所示 , △ABC 是等腰三角形 ,AB =AC. D ,E 分别是腰AB 及 AC 延长线上的一点 ,且 BD = CE ,连接 DE 交底 BC 于 G. 求证 :GD =GE .
图 1-1-25
图 1-1-26
发散思维
(1) ①如图 1-1-27 ( a) 所示 , 在 Rt △ABC 中 , ∠ACB =90 ° , 点 D , E 在边 AB 上 , 且 AD =AC , BE = BC , 求 ∠DCE 的度数.
②如图 1-1-27( b) 所示 ,在△ABC 中 , ∠ACB =40 ° ,点 D ,E 在直线 AB 上 ,且 AD =AC ,BE =BC ,求 ∠DCE 的度数.
图 1-1-27
(2) 在△ABC 中 , ∠ACB=n ° (0 < n < 180) ,点 D、点 E 在直线AB 上 ,且 AD=AC ,BE=BC ,求 ∠DCE 的度数 ( 直接写出答案 ,用含 n 的式子表示) .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
