第3章 图形的平移与旋转 评估检测题(单元测试)(无答案)八年级下册数学北师版
文档属性
| 名称 | 第3章 图形的平移与旋转 评估检测题(单元测试)(无答案)八年级下册数学北师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 106.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览

文档简介
第 3 章评估检测题
( 时间 :90 分钟 总分:100 分)
1 . 选择题(把正确答案的序号填在括号里) ( 每题 3 分 ,共 30 分)
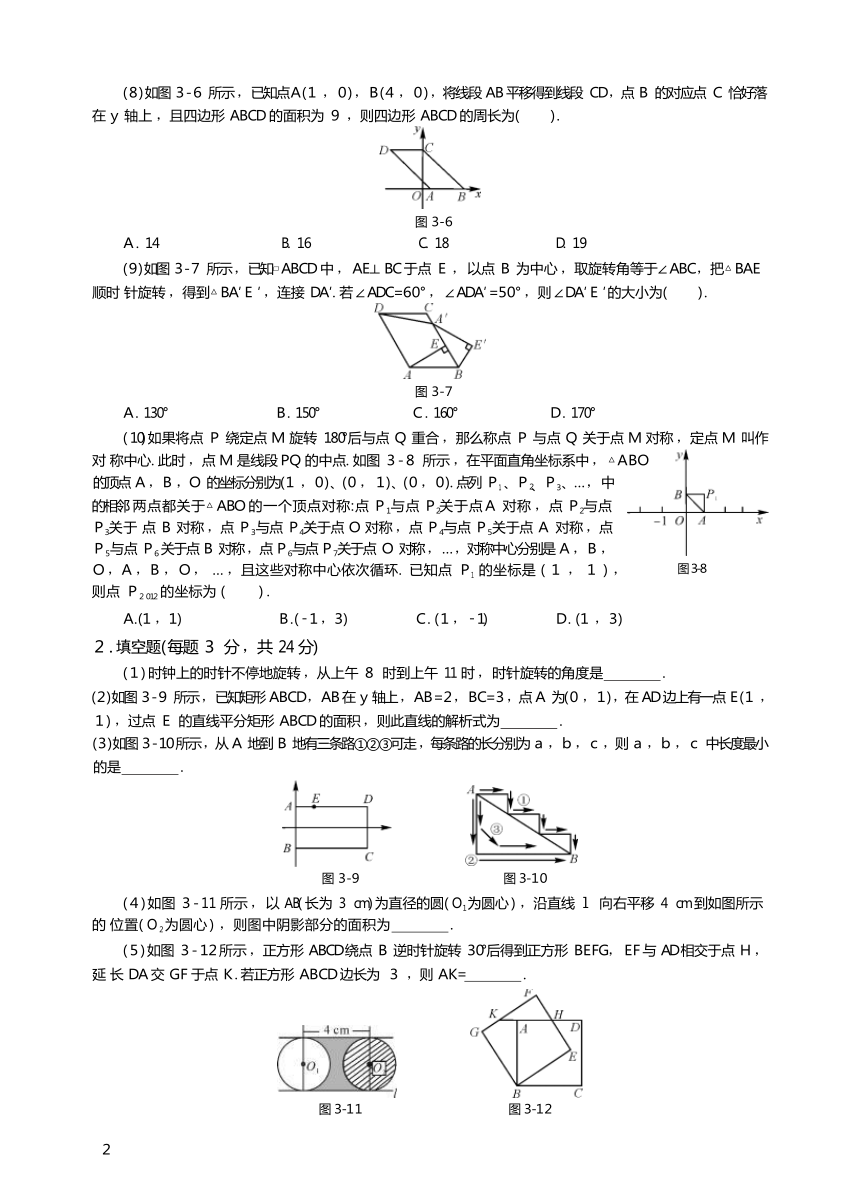
(1) 下列汽车标志中 ,是中心对称图形但不是轴对称图形的有( ) .
A . 2 个 B . 3 个 C . 4 个 D . 5 个
(2) 如图 3-1 所示 ,正六边形 ABCDEF 中 ,能够由△AOB 平移得到的三角形有( ) .
A . 1 个 B . 2 个 C . 3 个 D . 4 个
(3) 如图 3-2 所示 , 图形旋转一定角度后能与自身重合 ,则旋转的角度可能是( ) .
A . 30 ° B . 60 ° C . 90 ° D . 120 °
1
图 3-1
图 3-2
(
围是(
)
.
)(4) 将平面直角坐标系中的点P( a-2 ,2a +1)向左平移 1 个单位长度后位于第二象限 ,则 a 的取值范
A . 0 < a < 2 D .
(5) 如图 3-3 所示 ,长方形ABCD 是某公园里一处风景欣赏区 ,AB 长 50 m ,BC 宽25 m ,为方便游人观赏 , 公园特意修建了如图所示的小路 ,小路的宽均为 1 m ,那小明沿着小路的中间 ,从出 口 A 到出 口 B 所走的路 线( 图中虚线) 长为( ) .
A . 100 m B . 99 m C . 98 m D . 74 m
(6) 如图 3-4 所示 ,关于小船图案说法正确的是( ) .
A . 将小船乙左移 6 个单位长度就可以得到小船甲
B . 将小船甲右移 2 个单位长度就可以得到小船乙
C . 将小船甲先向右平移 4 个单位长度 ,再向上平移 1 个单位长度后就可以得到小船乙
D . 将小船乙先向左平移 2 个单位长度 ,再向下平移 1 个单位长度后就可以得到小船甲
图 3-3
图 3-4
(7) 分别以正方形的各边为直径向其内部作半圆得到的图形如图 3-5 所示 ,将该图形绕其中心旋转一个 合适的角度后会与原图形重合 ,则这个旋转角的最小度数是( ) .
图 3-5
A . 45 ° B . 90 ° C . 135 ° D . 180 °
(8) 如图 3-6 所示 , 已知点A(1 ,0) ,B(4 ,0) ,将线段 AB 平移得到线段 CD ,点 B 的对应点 C 恰好落在 y 轴上 ,且四边形 ABCD 的面积为 9 ,则四边形 ABCD 的周长为( ) .
图 3-6
A . 14 B . 16 C . 18 D . 19
(9) 如图 3-7 所示 , 已知 ABCD 中 ,AE⊥BC 于点 E , 以点 B 为中心 ,取旋转角等于∠ABC ,把△BAE 顺时 针旋转 ,得到△BA ′E ′ ,连接 DA ′. 若 ∠ADC=60 ° , ∠ADA ′=50 ° ,则 ∠DA ′E ′ 的大小为( ) .
图 3-7
A . 130 ° B . 150 ° C . 160 ° D . 170 °
(10) 如果将点 P 绕定点 M 旋转 180°后与点 Q 重合 ,那么称点 P 与点 Q 关于点 M 对称 ,定点 M 叫作对 称中心. 此时 ,点 M 是线段PQ 的中点. 如图 3-8 所示 ,在平面直角坐标系中 , △ABO
(
图
3-
8
)的顶点 A ,B ,O 的坐标分别为(1 ,0) 、(0 , 1) 、(0 ,0) . 点列 P 1 、P 2、P 3 、… , 中的相邻 两点都关于△ABO 的一个顶点对称:点 P 1 与点 P 2 关于点A 对称 ,点 P 2 与点 P 3 关于 点 B 对称 ,点 P 3 与点 P 4 关于点 O 对称 ,点 P 4 与点 P 5 关于点 A 对称 ,点 P 5 与点 P 6 关于点 B 对称 ,点 P 6 与点 P 7 关于点 O 对称 , … ,对称中心分别是 A ,B , O ,A ,B , O , … ,且这些对称中心依次循环. 已知点 P 1 的坐标是 ( 1 , 1 ) , 则点 P 2 012 的坐标为 ( ) .
A . (1 ,1) B . ( -1 ,3) C . ( 1 , -1) D . (1 ,3)
2 . 填空题( 每题 3 分 ,共 24 分)
(1) 时钟上的时针不停地旋转 ,从上午 8 时到上午 11 时 , 时针旋转的角度是 .
(2) 如图 3-9 所示 , 已知矩形 ABCD ,AB 在 y 轴上 ,AB =2 ,BC=3 ,点 A 为(0 ,1) ,在 AD 边上有一点 E(1 ,
1) ,过点 E 的直线平分矩形 ABCD 的面积 ,则此直线的解析式为 .
(3) 如图 3-10 所示 ,从 A 地到 B 地有三条路①②③可走 ,每条路的长分别为 a ,b ,c ,则 a ,b ,c 中长度最小
的是 .
2
图 3-9
图 3-10
(4) 如图 3-11 所示 , 以 AB( 长为 3 cm ) 为直径的圆( O 1 为圆心 ) ,沿直线 l 向右平移 4 cm 到如图所示的 位置( O 2 为圆心 ) ,则图中阴影部分的面积为 .
(5) 如图 3-12 所示 ,正方形 ABCD 绕点 B 逆时针旋转 30°后得到正方形 BEFG ,EF 与 AD 相交于点 H ,延 长 DA 交 GF 于点 K. 若正方形 ABCD 边长为 3 ,则 AK= .
图 3-11
图 3-12
(6) 任意一个正整数旋转 180°后 ,可以发现有趣的现象 ,如 808 旋转 180°后仍是 808 ,169 旋转 180°后成 691 ,而 37 旋转 180°就不是数了 ,则所有的五位数中旋转 180°后 ,还是原来的五位数共有 个.
(7) 将 5 个边长都为 1 cm 的正方形按如图 3-13 所示的样子摆放 ,点 A ,B , C ,D 分别是四个正方形的中 心 ,则图中四块阴影部分的面积的和为 cm 2 .
(8) 如图 3-14 所示 ,在直角梯形 ABCD 中 ,AD∥BC ,AB⊥BC ,AD =2 ,BC=4 , ∠BCD =45 ° ,将腰 CD 以点 D 为中心逆时针旋转 90°至 ED ,连接AE ,CE ,则△ADE 的面积是 .
3
图 3-13
图 3-14
3 . 解答题( 共 46 分)
(1) 如图 3-15 所示 , △ABC 与△A ′B ′ C ′关于点 O 中心对称 ,但点 O 不慎被涂掉了 ,请你找到对称中心 O
的位置. (8 分)
图 3-15
(2) 如图 3-16 所示 ,把一个三角尺ABC 绕着 30°角的顶点 B 顺时针旋转 ,使得点 A 旋转到 CB 的延长线 上的点 E . (8 分)
①三角尺旋转了多少度
②判断△BCD 的形状.
③求出∠ACD 的度数.
图 3-16
(3) 如图 3 ̄ 17 所示 ,将图中的点( -5 ,2) , ( -3 ,4) , ( -1 ,2) , ( -4 ,2) , ( -2 ,2) , ( -2 ,3) , ( -4 ,3 ) 做 如下变化. (8 分)
①横坐标不变 ,纵坐标分别减 4 ,再将所得的点用线段依次连接起来 ,所得的图形与原来的图形相比有 什么变化
②纵坐标不变 ,横坐标分别加 6 ,再将所得的点用线段依次连接起来 ,所得的图形与原来的图形相比有 什么变化
③求出以点( -5 ,2) , ( -3 ,4) , ( -1 ,2) 为顶点的三角形的面积
图 3-17
(4) 如图 3 ̄ 18 所示 , 已知△ABC 和△AEF 中 , ∠B = ∠E ,AB =AE ,BC =EF , ∠EAB =25 ° , ∠F =57 ° . ( 10 分)
①请说明∠EAB = ∠FAC 的理由.
②△ABC 可以经过图形的变换得到△AEF ,请你描述这个变换.
③求∠AMB 的度数.
图 3  ̄ 18
4
(5) 如图 3-19 所示 ,小明将一张矩形纸片沿对角线剪开 ,得到两张三角形纸片 ,量得它们的斜边长为 10 cm ,较短的边长为 5 cm ,较小的锐角为 30 ° ,再将这两张三角纸片摆成如图( a) 所示的形状 ,使点 B ,C ,D 在同 一条直线上 ,小明在对这两张三角形纸片进行如下操作时遇到了三个问题. ( 12 分)
①将图( b) 中的△ABC 沿 BD 向右平移到图 3-19-2 的位置 ,使点 B 与点 C 重合 ,请你求出平移的距离.
②将图( c) 中的△ABC 绕点 C 顺时针方向旋转 30°到图 3-19-3 的位置 ,AC 交 DE 于 M ,请你求出线段 CM 的长度.
③将图(d)中的△ABC 沿直线AC 翻折到图 3-19-4 的位置 ,AB 交 DE 于 N ,请证明:AN=DN.
( a) ( b) ( c) ( d)
图 3-19
5
( 时间 :90 分钟 总分:100 分)
1 . 选择题(把正确答案的序号填在括号里) ( 每题 3 分 ,共 30 分)
(1) 下列汽车标志中 ,是中心对称图形但不是轴对称图形的有( ) .
A . 2 个 B . 3 个 C . 4 个 D . 5 个
(2) 如图 3-1 所示 ,正六边形 ABCDEF 中 ,能够由△AOB 平移得到的三角形有( ) .
A . 1 个 B . 2 个 C . 3 个 D . 4 个
(3) 如图 3-2 所示 , 图形旋转一定角度后能与自身重合 ,则旋转的角度可能是( ) .
A . 30 ° B . 60 ° C . 90 ° D . 120 °
1
图 3-1
图 3-2
(
围是(
)
.
)(4) 将平面直角坐标系中的点P( a-2 ,2a +1)向左平移 1 个单位长度后位于第二象限 ,则 a 的取值范
A . 0 < a < 2 D .
(5) 如图 3-3 所示 ,长方形ABCD 是某公园里一处风景欣赏区 ,AB 长 50 m ,BC 宽25 m ,为方便游人观赏 , 公园特意修建了如图所示的小路 ,小路的宽均为 1 m ,那小明沿着小路的中间 ,从出 口 A 到出 口 B 所走的路 线( 图中虚线) 长为( ) .
A . 100 m B . 99 m C . 98 m D . 74 m
(6) 如图 3-4 所示 ,关于小船图案说法正确的是( ) .
A . 将小船乙左移 6 个单位长度就可以得到小船甲
B . 将小船甲右移 2 个单位长度就可以得到小船乙
C . 将小船甲先向右平移 4 个单位长度 ,再向上平移 1 个单位长度后就可以得到小船乙
D . 将小船乙先向左平移 2 个单位长度 ,再向下平移 1 个单位长度后就可以得到小船甲
图 3-3
图 3-4
(7) 分别以正方形的各边为直径向其内部作半圆得到的图形如图 3-5 所示 ,将该图形绕其中心旋转一个 合适的角度后会与原图形重合 ,则这个旋转角的最小度数是( ) .
图 3-5
A . 45 ° B . 90 ° C . 135 ° D . 180 °
(8) 如图 3-6 所示 , 已知点A(1 ,0) ,B(4 ,0) ,将线段 AB 平移得到线段 CD ,点 B 的对应点 C 恰好落在 y 轴上 ,且四边形 ABCD 的面积为 9 ,则四边形 ABCD 的周长为( ) .
图 3-6
A . 14 B . 16 C . 18 D . 19
(9) 如图 3-7 所示 , 已知 ABCD 中 ,AE⊥BC 于点 E , 以点 B 为中心 ,取旋转角等于∠ABC ,把△BAE 顺时 针旋转 ,得到△BA ′E ′ ,连接 DA ′. 若 ∠ADC=60 ° , ∠ADA ′=50 ° ,则 ∠DA ′E ′ 的大小为( ) .
图 3-7
A . 130 ° B . 150 ° C . 160 ° D . 170 °
(10) 如果将点 P 绕定点 M 旋转 180°后与点 Q 重合 ,那么称点 P 与点 Q 关于点 M 对称 ,定点 M 叫作对 称中心. 此时 ,点 M 是线段PQ 的中点. 如图 3-8 所示 ,在平面直角坐标系中 , △ABO
(
图
3-
8
)的顶点 A ,B ,O 的坐标分别为(1 ,0) 、(0 , 1) 、(0 ,0) . 点列 P 1 、P 2、P 3 、… , 中的相邻 两点都关于△ABO 的一个顶点对称:点 P 1 与点 P 2 关于点A 对称 ,点 P 2 与点 P 3 关于 点 B 对称 ,点 P 3 与点 P 4 关于点 O 对称 ,点 P 4 与点 P 5 关于点 A 对称 ,点 P 5 与点 P 6 关于点 B 对称 ,点 P 6 与点 P 7 关于点 O 对称 , … ,对称中心分别是 A ,B , O ,A ,B , O , … ,且这些对称中心依次循环. 已知点 P 1 的坐标是 ( 1 , 1 ) , 则点 P 2 012 的坐标为 ( ) .
A . (1 ,1) B . ( -1 ,3) C . ( 1 , -1) D . (1 ,3)
2 . 填空题( 每题 3 分 ,共 24 分)
(1) 时钟上的时针不停地旋转 ,从上午 8 时到上午 11 时 , 时针旋转的角度是 .
(2) 如图 3-9 所示 , 已知矩形 ABCD ,AB 在 y 轴上 ,AB =2 ,BC=3 ,点 A 为(0 ,1) ,在 AD 边上有一点 E(1 ,
1) ,过点 E 的直线平分矩形 ABCD 的面积 ,则此直线的解析式为 .
(3) 如图 3-10 所示 ,从 A 地到 B 地有三条路①②③可走 ,每条路的长分别为 a ,b ,c ,则 a ,b ,c 中长度最小
的是 .
2
图 3-9
图 3-10
(4) 如图 3-11 所示 , 以 AB( 长为 3 cm ) 为直径的圆( O 1 为圆心 ) ,沿直线 l 向右平移 4 cm 到如图所示的 位置( O 2 为圆心 ) ,则图中阴影部分的面积为 .
(5) 如图 3-12 所示 ,正方形 ABCD 绕点 B 逆时针旋转 30°后得到正方形 BEFG ,EF 与 AD 相交于点 H ,延 长 DA 交 GF 于点 K. 若正方形 ABCD 边长为 3 ,则 AK= .
图 3-11
图 3-12
(6) 任意一个正整数旋转 180°后 ,可以发现有趣的现象 ,如 808 旋转 180°后仍是 808 ,169 旋转 180°后成 691 ,而 37 旋转 180°就不是数了 ,则所有的五位数中旋转 180°后 ,还是原来的五位数共有 个.
(7) 将 5 个边长都为 1 cm 的正方形按如图 3-13 所示的样子摆放 ,点 A ,B , C ,D 分别是四个正方形的中 心 ,则图中四块阴影部分的面积的和为 cm 2 .
(8) 如图 3-14 所示 ,在直角梯形 ABCD 中 ,AD∥BC ,AB⊥BC ,AD =2 ,BC=4 , ∠BCD =45 ° ,将腰 CD 以点 D 为中心逆时针旋转 90°至 ED ,连接AE ,CE ,则△ADE 的面积是 .
3
图 3-13
图 3-14
3 . 解答题( 共 46 分)
(1) 如图 3-15 所示 , △ABC 与△A ′B ′ C ′关于点 O 中心对称 ,但点 O 不慎被涂掉了 ,请你找到对称中心 O
的位置. (8 分)
图 3-15
(2) 如图 3-16 所示 ,把一个三角尺ABC 绕着 30°角的顶点 B 顺时针旋转 ,使得点 A 旋转到 CB 的延长线 上的点 E . (8 分)
①三角尺旋转了多少度
②判断△BCD 的形状.
③求出∠ACD 的度数.
图 3-16
(3) 如图 3 ̄ 17 所示 ,将图中的点( -5 ,2) , ( -3 ,4) , ( -1 ,2) , ( -4 ,2) , ( -2 ,2) , ( -2 ,3) , ( -4 ,3 ) 做 如下变化. (8 分)
①横坐标不变 ,纵坐标分别减 4 ,再将所得的点用线段依次连接起来 ,所得的图形与原来的图形相比有 什么变化
②纵坐标不变 ,横坐标分别加 6 ,再将所得的点用线段依次连接起来 ,所得的图形与原来的图形相比有 什么变化
③求出以点( -5 ,2) , ( -3 ,4) , ( -1 ,2) 为顶点的三角形的面积
图 3-17
(4) 如图 3 ̄ 18 所示 , 已知△ABC 和△AEF 中 , ∠B = ∠E ,AB =AE ,BC =EF , ∠EAB =25 ° , ∠F =57 ° . ( 10 分)
①请说明∠EAB = ∠FAC 的理由.
②△ABC 可以经过图形的变换得到△AEF ,请你描述这个变换.
③求∠AMB 的度数.
图 3  ̄ 18
4
(5) 如图 3-19 所示 ,小明将一张矩形纸片沿对角线剪开 ,得到两张三角形纸片 ,量得它们的斜边长为 10 cm ,较短的边长为 5 cm ,较小的锐角为 30 ° ,再将这两张三角纸片摆成如图( a) 所示的形状 ,使点 B ,C ,D 在同 一条直线上 ,小明在对这两张三角形纸片进行如下操作时遇到了三个问题. ( 12 分)
①将图( b) 中的△ABC 沿 BD 向右平移到图 3-19-2 的位置 ,使点 B 与点 C 重合 ,请你求出平移的距离.
②将图( c) 中的△ABC 绕点 C 顺时针方向旋转 30°到图 3-19-3 的位置 ,AC 交 DE 于 M ,请你求出线段 CM 的长度.
③将图(d)中的△ABC 沿直线AC 翻折到图 3-19-4 的位置 ,AB 交 DE 于 N ,请证明:AN=DN.
( a) ( b) ( c) ( d)
图 3-19
5
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
