人教版九年级数学下册 期末测试卷 (含详解)
文档属性
| 名称 | 人教版九年级数学下册 期末测试卷 (含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 14:09:40 | ||
图片预览



文档简介
期末测试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.的相反数是( )
A. B. C. D.
2.函数中,自变量x的取值范围是( )
A. B.且 C. D.且
3.据报道,截止到2020年12月31日,国外累计确诊感染新冠病毒人数已超过人,数据用科学计数法表示为( )
A. B. C. D.
4.已知是方程的一个解,那么的值是( )
A. B. C.1 D.2
5.已知一次函数,若y随x的增大而减小,则m的取值范围是( ).
A. B. C. D.
6.如图,中,在的延长线上,过作于,交于.已知,,则( )
A. B. C. D.
7.若与的相似比为,则与的相似比为( )
A. B. C. D.
8.正六边形的外角和为( )
A.180° B.360° C.720° D.1080°
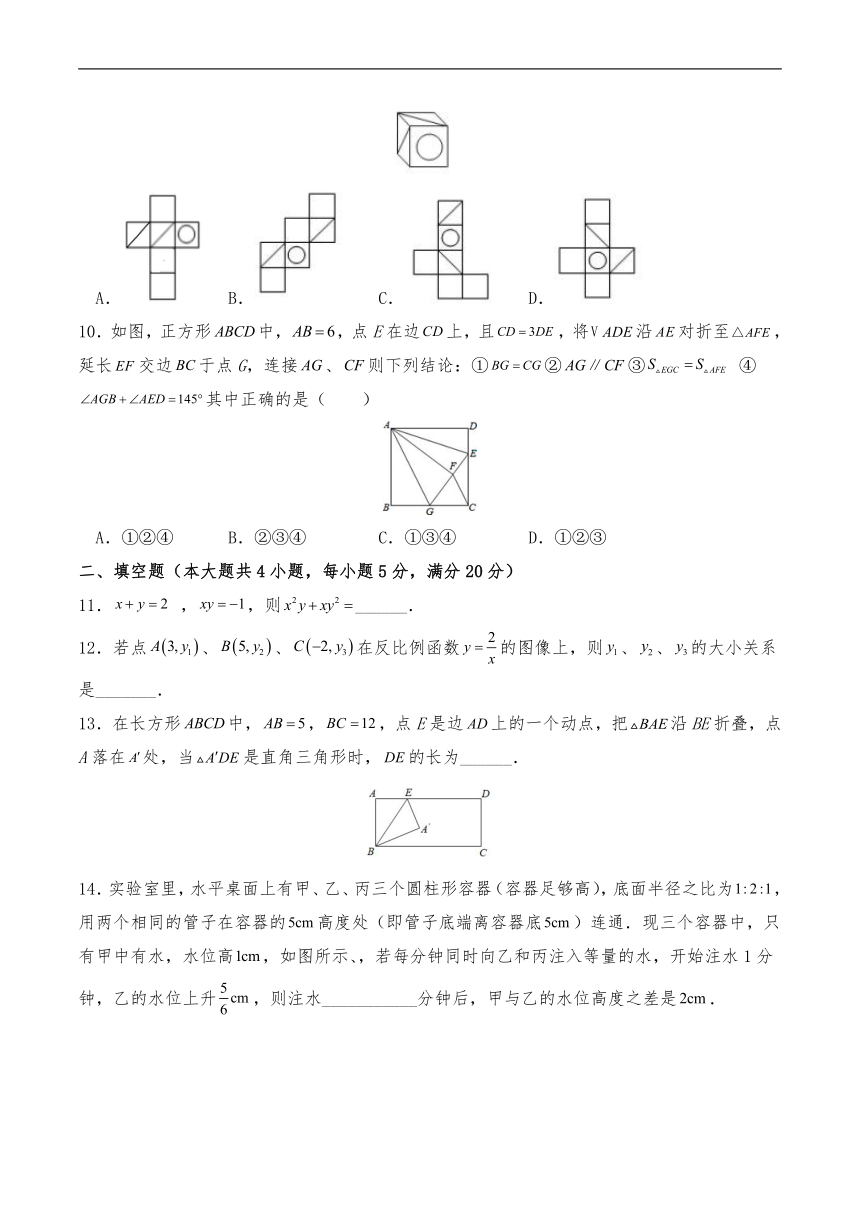
9.如图所示的正方体的展开图是( )
A. B. C. D.
10.如图,正方形中,,点E在边上,且,将沿对折至,延长交边于点G,连接、则下列结论:①②③ ④其中正确的是( )
A.①②④ B.②③④ C.①③④ D.①②③
二、填空题(本大题共4小题,每小题5分,满分20分)
11. ,,则______.
12.若点、、在反比例函数的图像上,则、、的大小关系是_______.
13.在长方形中,,,点E是边上的一个动点,把沿BE折叠,点A落在处,当是直角三角形时,的长为______.
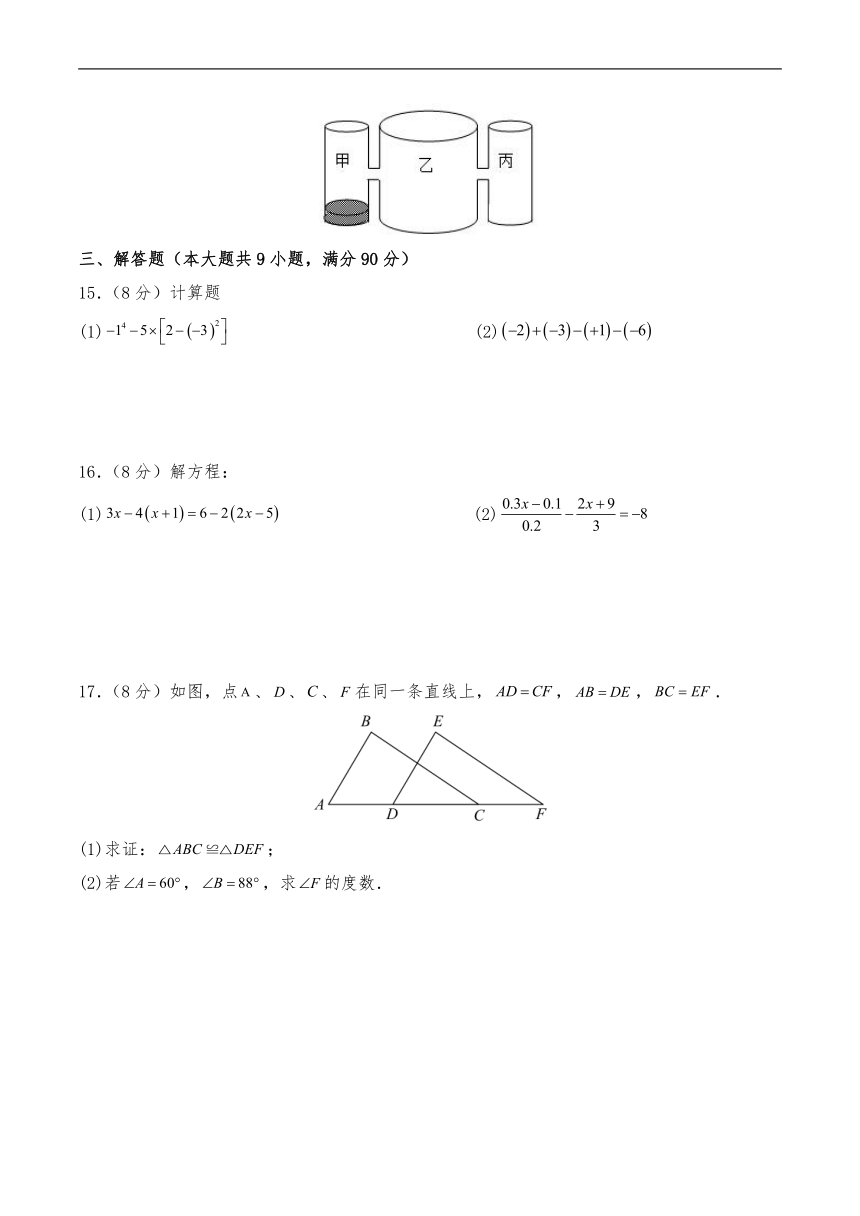
14.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为,用两个相同的管子在容器的高度处(即管子底端离容器底)连通.现三个容器中,只有甲中有水,水位高,如图所示、,若每分钟同时向乙和丙注入等量的水,开始注水1分钟,乙的水位上升,则注水___________分钟后,甲与乙的水位高度之差是.
三、解答题(本大题共9小题,满分90分)
15.(8分)计算题
(1) (2)
16.(8分)解方程:
(1) (2)
17.(8分)如图,点、、、在同一条直线上,,,.
(1)求证:;
(2)若,,求的度数.
18.(10分)如图,为的直径,弦于E,连接,过A作,交于点F,连接,过B作,交的延长线于点G.
(1)求证:是的切线;
(2)若,,求阴影部分的面积.
19.(10分)农历正月十五元宵节有吃汤元的习俗、小华的妈妈在包的48个汤元中,有两个汤元用红枣做馅,与其它汤元不同馅、现每碗盛8个汤元,共盛6碗,且两个红枣汤圆被盛到不同的碗里,小华吃2碗,
(1)小华吃的两碗中都有红枣汤元的概率;
(2)小华吃到红枣汤元的概率.
20.(10分)某市初级中学在开展“疫情防控,从我做起”的活动中,为了了解该校学生对疫情防控知识的了解程度,现对该校学生进行随机抽样调查,调查结果分为四种:A.非常了解, B.比较了解, C.基本了解, D.不太了解.整理数据并绘制了如下不完整的统计图.
请结合图中所给信息解答下列问题:
(1)本次共调查了 名学生;扇形统计图中,C所对应的扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)该校共有名学生,根据以上信息,请你估计全校学生对疫情防控知识“非常了解“和“比较了解“的共有多少名?
21.(10分)为了丰富学生的课外活动,某校决定购买一批体育活动用品,经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副球拍贵50元,两个篮球与三副球拍的费用相等,经洽谈,甲体育用品商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球超过80个,则购买羽毛球拍打八折.该校购买100个篮球和a()副羽毛球拍.
(1)求每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的式子分别表示出到甲商店和乙商店购买体育活动用品所花的费用.
(3)当该校购买多少副羽毛球拍时,在甲、乙两个商店购买所需费用一样?
22.(12分)如图1,梯形中,,,,,,M在边上,连接,;
(1)求的长;
(2)如图2,作,交于点E,交于点F,若,,求y关于x的函数解析式,并写出定义域;
(3)若是等腰三角形,求的值;
23.(14分)如图,在直角坐标系中有,为坐标原点,,,将此三角形绕原点顺时针旋转,得到,二次函数的图象刚好经过,,三点.
(1)求二次函数的解析式及顶点的坐标;
(2)过定点的直线与二次函数图象相交于M,两点.
①若,求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
答案
一、选择题
1.B
【详解】解:的相反数是,
故选:.
2.D
【详解】解:根据题意得:,
解得:且.
故选:D
3.C
【详解】解:.
故选:C.
4.C
【详解】解:把代入方程得:
,
解得:;
故选:C.
5.C
【详解】解:∵一次函数,y随x的增大而减小,
∴,
解得:,故C正确.
故选:C.
6.D
【详解】解:,
,
在中,,,
,
又,
,
在中,,,
.
故选:D.
7.C
【详解】解:∵与的相似比为,
∴与的相似比为,
故选C.
8.B
【详解】任意凸多边形的外角和为360°,
∴正六边形的外角和为360°,
故选:B.
9.D
【详解】解:根据正方体的平面展开图的特征,
A选项折叠后“圆”和“三角形”是相对面,不符合题意;
B选项折叠后“三角形”和“三角形”是相对面,不符合题意;
C选项折叠后“三角形”和“三角形”是相对面,不符合题意;
D选项折叠后符合题意,
∴是该正方体的展开图的是D选项,
故选:D.
10.D
【详解】∵四边形为正方形,将沿对折至,
∴,,
∴,
∵,,
∴,
∴,
∵,
∴,,
设,则,
在直角△ECG中,根据勾股定理,得,
解得.
∴,
∴①正确;
∵,,
∴,
∴是等腰三角形,
∴.
又∵;
∴,
,
∴,
∴,
∴②正确;
∵,
,
∴,
∴③正确;
∵,,
又∵,
∴,
∴,
∴④错误.
故选:D.
二、填空题
11.
【详解】解:,
∵,
∴原式.
故答案为:.
12.
【详解】解:∵反比例函数的解析式是,
∴,函数的图像在第一、三象限,且在每个象限内,y随x的增大而减小,
∵点、、在反比例函数的图像上,
∴点A和B在第一象限,点C在第三象限,
∴.
故答案为:.
13.
【详解】解:∵四边形是矩形,,
, ,
当在上时,是直角三角形,如图1所示:
设,
由翻折的性质得:,
,
,
在中,
,
解得:,即
14.,
【详解】解:∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为,且注水1分钟,乙的水位上升,
∴注水1分钟,丙的水位上升,
设开始注入t分钟的水量后,甲与乙的水位高度之差为2cm,则可分:
①当甲的水位低于乙的水位时,甲的水位不变时,则有:
∴,解得:;
∵,
∴此时丙容器已向乙容器溢水,
∵分钟,cm,即经过分钟丙容器的水达到管子底部,乙的水位上升cm,
∴,
解得:;
②当甲的水位低于乙的水位时,乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为:分钟,
∴,
解得:;
综上所述:开始注入,分钟的水量后,甲乙的水位高度之差是2cm;
故答案为,.
三、解答题
15.(1)解:原式
;
(2)原式
.
16.(1)解:
去括号得:,
移项得:,
合并同类项得:,
系数化为1得;;
(2)解:
整理得:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得;.
17.(1)证明:∵,
∴,即,
在和中,
,
∴;
(2)解:∵,,
∴,
∵,
∴.
18.(1)证明:∵C,A,D,F在⊙O上,,
∴,
∵,,
∴,∴四边形中,,
∴半径,
∴是的切线;
(2)解:连接,
∵,
∴是的直径,
∴,
∵直径于E,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∵,
∴E为的中点,
∴,,,
∴,,
∵,
∴四边形是矩形,
∴
.
19.(1)解:每碗盛8个汤元,48个汤元共可盛6碗,用A、B、C、D、E、F分别表示6碗汤元,则小华吃两碗,所有可能为:
共15种,设A,B中含有红枣汤圆,
∴小华吃的两碗中都有红枣汤元的概率是;
(2)解:由(1)可知,吃到红枣汤圆的情况有9种,所以概率是.
20.(1)解:由题意可得,
本次调查的总人数为:(人),
C所对应的扇形百分比为:,
扇形统计图中,C所对应的扇形的圆心角度数是:,
故答案为:;;
(2)解:由(1)可得,
B的百分比为:,
B的人数为:(人),
(人),
∴直方图如下图所示:
;
(3)解:由题意可得,
“非常了解“和“比较了解“的共有:(人).
21.(1)解:设每个篮球的定价是元,则每幅羽毛球拍是元,根据题意得
,
解得,
.
答:每副羽毛球拍100元,每个篮球150元.
(2)解:到甲商店购买所花的费用为:元;
到乙商店购买所花的费用为:元;
(3)解:当在两家商店购买一样合算时,有
,
解得.
所以购买50副羽毛球拍时,在甲、乙两个商店购买所需费用一样.
22.(1)解:过点D作于点P,
∵,,
∴,
∵,
∴,
∴四边形为矩形,
∴,,
∵,
∴,
在中,根据勾股定理得:.
(2)解:连接,
∵,,
∴,
即,解得:,
在和中,
,
∴Rt ABD≌Rt MBD(HL),
∴,
∴,
∵,
∴,,
∵,,
∴,
∴,,
∴ MBE∽ MCF,
∴,,
整理得:.
(3)①当点E在线段上时,
由(2)可得 MBE∽ MCF,
∵为等腰三角形,
∴为等腰三角形,
当时,;
当时,过点M作于点Q,
由(1)可得:,
∴,
∵,
∴,
∵,,
∴,不符合题意,舍去;=
当时,过点E作于点H,
∵,,
∴,
∵,
∴,
∴,
②当点E在延长线上时,
∵,,
∴,
∴当点E在延长线上时,只能为等腰三角形的顶角,
∴,
∴.
综上:或或8.
23.(1)解:,
,
根据旋转的性质可得:,
,
把、分别代入解析式,得
,
解得:,
二次函数的解析式为,
,
顶点坐标为;
(2)解:①设,
直线:过定点,抛物线的顶点坐标为,
,
,
,
联立
得,
,
,
;
②证明:过点作轴,垂足为,分别过点,作的垂线,垂足分别为、,
设.
,在二次函数图象上,
,.
∵P(1,4),
,,,,
,
,
由①可知,
,
,
,
,
,
,
,即,
无论为何值,恒为直角三角形;
③解:∵恒为直角三角形,,
∴外接圆圆心是线段的中点;
设线段的中点,
∵,,.
∴
∴的中点为,
,
化简,得,
抛物线的表达式为.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.的相反数是( )
A. B. C. D.
2.函数中,自变量x的取值范围是( )
A. B.且 C. D.且
3.据报道,截止到2020年12月31日,国外累计确诊感染新冠病毒人数已超过人,数据用科学计数法表示为( )
A. B. C. D.
4.已知是方程的一个解,那么的值是( )
A. B. C.1 D.2
5.已知一次函数,若y随x的增大而减小,则m的取值范围是( ).
A. B. C. D.
6.如图,中,在的延长线上,过作于,交于.已知,,则( )
A. B. C. D.
7.若与的相似比为,则与的相似比为( )
A. B. C. D.
8.正六边形的外角和为( )
A.180° B.360° C.720° D.1080°
9.如图所示的正方体的展开图是( )
A. B. C. D.
10.如图,正方形中,,点E在边上,且,将沿对折至,延长交边于点G,连接、则下列结论:①②③ ④其中正确的是( )
A.①②④ B.②③④ C.①③④ D.①②③
二、填空题(本大题共4小题,每小题5分,满分20分)
11. ,,则______.
12.若点、、在反比例函数的图像上,则、、的大小关系是_______.
13.在长方形中,,,点E是边上的一个动点,把沿BE折叠,点A落在处,当是直角三角形时,的长为______.
14.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为,用两个相同的管子在容器的高度处(即管子底端离容器底)连通.现三个容器中,只有甲中有水,水位高,如图所示、,若每分钟同时向乙和丙注入等量的水,开始注水1分钟,乙的水位上升,则注水___________分钟后,甲与乙的水位高度之差是.
三、解答题(本大题共9小题,满分90分)
15.(8分)计算题
(1) (2)
16.(8分)解方程:
(1) (2)
17.(8分)如图,点、、、在同一条直线上,,,.
(1)求证:;
(2)若,,求的度数.
18.(10分)如图,为的直径,弦于E,连接,过A作,交于点F,连接,过B作,交的延长线于点G.
(1)求证:是的切线;
(2)若,,求阴影部分的面积.
19.(10分)农历正月十五元宵节有吃汤元的习俗、小华的妈妈在包的48个汤元中,有两个汤元用红枣做馅,与其它汤元不同馅、现每碗盛8个汤元,共盛6碗,且两个红枣汤圆被盛到不同的碗里,小华吃2碗,
(1)小华吃的两碗中都有红枣汤元的概率;
(2)小华吃到红枣汤元的概率.
20.(10分)某市初级中学在开展“疫情防控,从我做起”的活动中,为了了解该校学生对疫情防控知识的了解程度,现对该校学生进行随机抽样调查,调查结果分为四种:A.非常了解, B.比较了解, C.基本了解, D.不太了解.整理数据并绘制了如下不完整的统计图.
请结合图中所给信息解答下列问题:
(1)本次共调查了 名学生;扇形统计图中,C所对应的扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)该校共有名学生,根据以上信息,请你估计全校学生对疫情防控知识“非常了解“和“比较了解“的共有多少名?
21.(10分)为了丰富学生的课外活动,某校决定购买一批体育活动用品,经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副球拍贵50元,两个篮球与三副球拍的费用相等,经洽谈,甲体育用品商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球超过80个,则购买羽毛球拍打八折.该校购买100个篮球和a()副羽毛球拍.
(1)求每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的式子分别表示出到甲商店和乙商店购买体育活动用品所花的费用.
(3)当该校购买多少副羽毛球拍时,在甲、乙两个商店购买所需费用一样?
22.(12分)如图1,梯形中,,,,,,M在边上,连接,;
(1)求的长;
(2)如图2,作,交于点E,交于点F,若,,求y关于x的函数解析式,并写出定义域;
(3)若是等腰三角形,求的值;
23.(14分)如图,在直角坐标系中有,为坐标原点,,,将此三角形绕原点顺时针旋转,得到,二次函数的图象刚好经过,,三点.
(1)求二次函数的解析式及顶点的坐标;
(2)过定点的直线与二次函数图象相交于M,两点.
①若,求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
答案
一、选择题
1.B
【详解】解:的相反数是,
故选:.
2.D
【详解】解:根据题意得:,
解得:且.
故选:D
3.C
【详解】解:.
故选:C.
4.C
【详解】解:把代入方程得:
,
解得:;
故选:C.
5.C
【详解】解:∵一次函数,y随x的增大而减小,
∴,
解得:,故C正确.
故选:C.
6.D
【详解】解:,
,
在中,,,
,
又,
,
在中,,,
.
故选:D.
7.C
【详解】解:∵与的相似比为,
∴与的相似比为,
故选C.
8.B
【详解】任意凸多边形的外角和为360°,
∴正六边形的外角和为360°,
故选:B.
9.D
【详解】解:根据正方体的平面展开图的特征,
A选项折叠后“圆”和“三角形”是相对面,不符合题意;
B选项折叠后“三角形”和“三角形”是相对面,不符合题意;
C选项折叠后“三角形”和“三角形”是相对面,不符合题意;
D选项折叠后符合题意,
∴是该正方体的展开图的是D选项,
故选:D.
10.D
【详解】∵四边形为正方形,将沿对折至,
∴,,
∴,
∵,,
∴,
∴,
∵,
∴,,
设,则,
在直角△ECG中,根据勾股定理,得,
解得.
∴,
∴①正确;
∵,,
∴,
∴是等腰三角形,
∴.
又∵;
∴,
,
∴,
∴,
∴②正确;
∵,
,
∴,
∴③正确;
∵,,
又∵,
∴,
∴,
∴④错误.
故选:D.
二、填空题
11.
【详解】解:,
∵,
∴原式.
故答案为:.
12.
【详解】解:∵反比例函数的解析式是,
∴,函数的图像在第一、三象限,且在每个象限内,y随x的增大而减小,
∵点、、在反比例函数的图像上,
∴点A和B在第一象限,点C在第三象限,
∴.
故答案为:.
13.
【详解】解:∵四边形是矩形,,
, ,
当在上时,是直角三角形,如图1所示:
设,
由翻折的性质得:,
,
,
在中,
,
解得:,即
14.,
【详解】解:∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为,且注水1分钟,乙的水位上升,
∴注水1分钟,丙的水位上升,
设开始注入t分钟的水量后,甲与乙的水位高度之差为2cm,则可分:
①当甲的水位低于乙的水位时,甲的水位不变时,则有:
∴,解得:;
∵,
∴此时丙容器已向乙容器溢水,
∵分钟,cm,即经过分钟丙容器的水达到管子底部,乙的水位上升cm,
∴,
解得:;
②当甲的水位低于乙的水位时,乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为:分钟,
∴,
解得:;
综上所述:开始注入,分钟的水量后,甲乙的水位高度之差是2cm;
故答案为,.
三、解答题
15.(1)解:原式
;
(2)原式
.
16.(1)解:
去括号得:,
移项得:,
合并同类项得:,
系数化为1得;;
(2)解:
整理得:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得;.
17.(1)证明:∵,
∴,即,
在和中,
,
∴;
(2)解:∵,,
∴,
∵,
∴.
18.(1)证明:∵C,A,D,F在⊙O上,,
∴,
∵,,
∴,∴四边形中,,
∴半径,
∴是的切线;
(2)解:连接,
∵,
∴是的直径,
∴,
∵直径于E,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∵,
∴E为的中点,
∴,,,
∴,,
∵,
∴四边形是矩形,
∴
.
19.(1)解:每碗盛8个汤元,48个汤元共可盛6碗,用A、B、C、D、E、F分别表示6碗汤元,则小华吃两碗,所有可能为:
共15种,设A,B中含有红枣汤圆,
∴小华吃的两碗中都有红枣汤元的概率是;
(2)解:由(1)可知,吃到红枣汤圆的情况有9种,所以概率是.
20.(1)解:由题意可得,
本次调查的总人数为:(人),
C所对应的扇形百分比为:,
扇形统计图中,C所对应的扇形的圆心角度数是:,
故答案为:;;
(2)解:由(1)可得,
B的百分比为:,
B的人数为:(人),
(人),
∴直方图如下图所示:
;
(3)解:由题意可得,
“非常了解“和“比较了解“的共有:(人).
21.(1)解:设每个篮球的定价是元,则每幅羽毛球拍是元,根据题意得
,
解得,
.
答:每副羽毛球拍100元,每个篮球150元.
(2)解:到甲商店购买所花的费用为:元;
到乙商店购买所花的费用为:元;
(3)解:当在两家商店购买一样合算时,有
,
解得.
所以购买50副羽毛球拍时,在甲、乙两个商店购买所需费用一样.
22.(1)解:过点D作于点P,
∵,,
∴,
∵,
∴,
∴四边形为矩形,
∴,,
∵,
∴,
在中,根据勾股定理得:.
(2)解:连接,
∵,,
∴,
即,解得:,
在和中,
,
∴Rt ABD≌Rt MBD(HL),
∴,
∴,
∵,
∴,,
∵,,
∴,
∴,,
∴ MBE∽ MCF,
∴,,
整理得:.
(3)①当点E在线段上时,
由(2)可得 MBE∽ MCF,
∵为等腰三角形,
∴为等腰三角形,
当时,;
当时,过点M作于点Q,
由(1)可得:,
∴,
∵,
∴,
∵,,
∴,不符合题意,舍去;=
当时,过点E作于点H,
∵,,
∴,
∵,
∴,
∴,
②当点E在延长线上时,
∵,,
∴,
∴当点E在延长线上时,只能为等腰三角形的顶角,
∴,
∴.
综上:或或8.
23.(1)解:,
,
根据旋转的性质可得:,
,
把、分别代入解析式,得
,
解得:,
二次函数的解析式为,
,
顶点坐标为;
(2)解:①设,
直线:过定点,抛物线的顶点坐标为,
,
,
,
联立
得,
,
,
;
②证明:过点作轴,垂足为,分别过点,作的垂线,垂足分别为、,
设.
,在二次函数图象上,
,.
∵P(1,4),
,,,,
,
,
由①可知,
,
,
,
,
,
,
,即,
无论为何值,恒为直角三角形;
③解:∵恒为直角三角形,,
∴外接圆圆心是线段的中点;
设线段的中点,
∵,,.
∴
∴的中点为,
,
化简,得,
抛物线的表达式为.
同课章节目录
