19.1变量与函数 同步练习(含答案) 2024-2025学年人教版数学八下
文档属性
| 名称 | 19.1变量与函数 同步练习(含答案) 2024-2025学年人教版数学八下 |

|
|
| 格式 | docx | ||
| 文件大小 | 149.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览


文档简介
19.1变量与函数 同步练习 2024-2025学年人教版数学八下
一、单选题
1.关于变量x,y有如下关系:①x-y=5;②y2=2x;③:y=|x|;④y=.其中y是x函数的是( )
A. B. C. D.
2.函数 中,自变量x的取值范围是( )
A.x≠0 B.x<1 C.x>1 D.x≠1
3.圆周长公式C=2πR中,下列说法正确的是( )
A.π、R是变量,2为常量 B.C、R为变量,2、π为常量
C.R为变量,2、π、C为常量 D.C为变量,2、π、R为常量
4.如图,用每张长为的纸片,重叠粘贴成一条纸带,则纸带的长度与纸片的张数x之间的函数关系式是( )
A. B. C. D.
5.汽车油箱中有汽油,如果不再加油,油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为.当时,y与x之间的关系式是( )
A. B.
C. D.
6.小明骑自行车上学,一开始以某一恒定的速度行驶,但行驶至途中自行车发生了故障,只好停下来修车,车修好后,因怕耽误了上课,他比修车前加快了骑车的速度,下面四幅图中最能反映小明这段行程的是( )
A. B.
C. D.
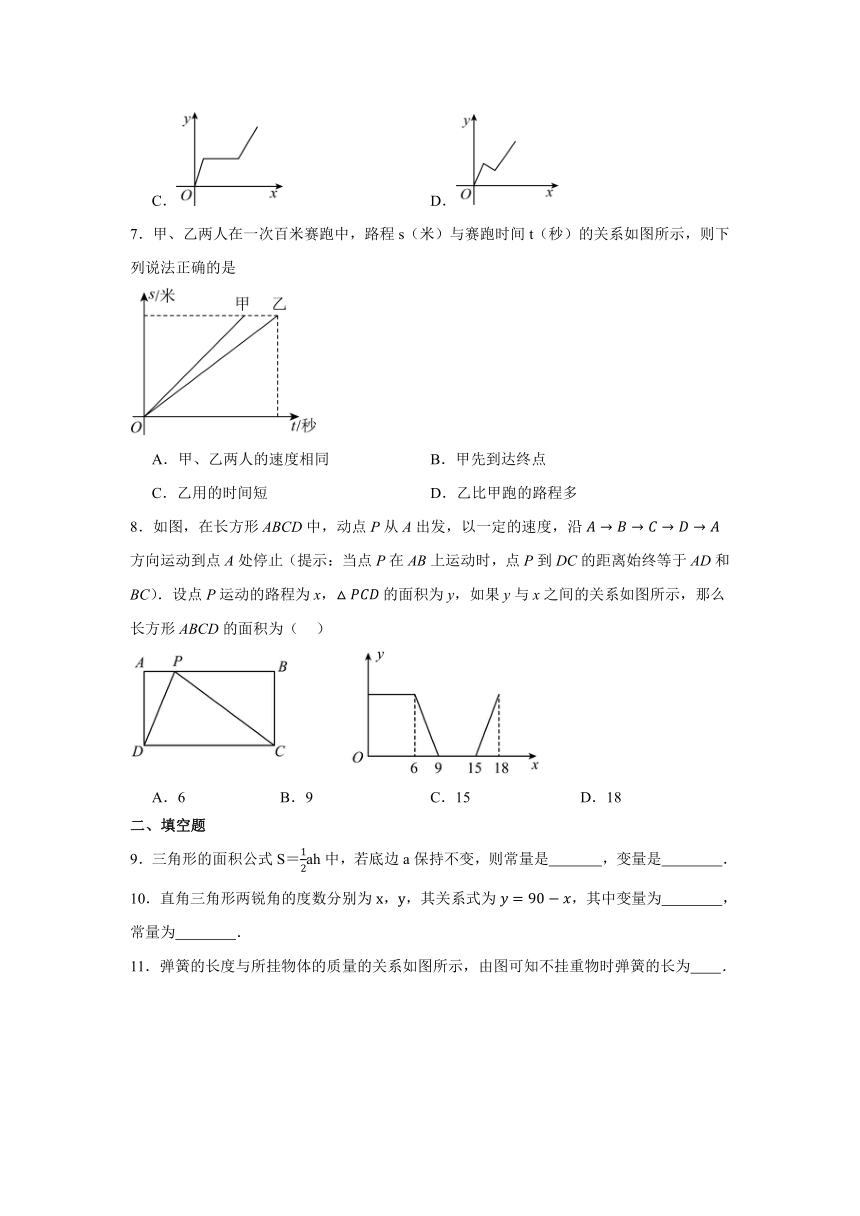
7.甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是
A.甲、乙两人的速度相同 B.甲先到达终点
C.乙用的时间短 D.乙比甲跑的路程多
8.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
二、填空题
9.三角形的面积公式S=ah中,若底边a保持不变,则常量是 ,变量是 .
10.直角三角形两锐角的度数分别为,,其关系式为,其中变量为 ,常量为 .
11.弹簧的长度与所挂物体的质量的关系如图所示,由图可知不挂重物时弹簧的长为 .
12.长方形的周长为20,宽为x.若设长方形的面积为S,则面积S与宽x之间的关系是 .
13.夏天高山上的气温从山脚起每升高l00m降低0.7℃,已知山脚下的气温是23℃,则气温y(℃)与上升的高度x(m)之间的关系式为 ;当x=500时,y= ;当y=16时,x= .
14.一种树苗栽种时的高度为80cm,为研究它们的生长情况,测得数据如表;
栽种以后的年数n/年 1 2 3 4 …
高度h/m 105 130 155 180 …
则按照表中呈现的规律,树苗的高度h与栽种年数n的关系式为 ,栽种 年后,树苗能长到280cm.
15.星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题:
(1)公共阅报栏离小红家有__________米,小红从家走到公共阅报栏用了__________分;
(2)小红在公共阅报栏看新闻一共用了__________分;
(3)邮亭离公共阅报栏有__________米,小红从公共阅报栏到邮亭用了__________分;
(4)小红从邮亭走回家用了__________分,平均速度是__________米/分.
三、解答题
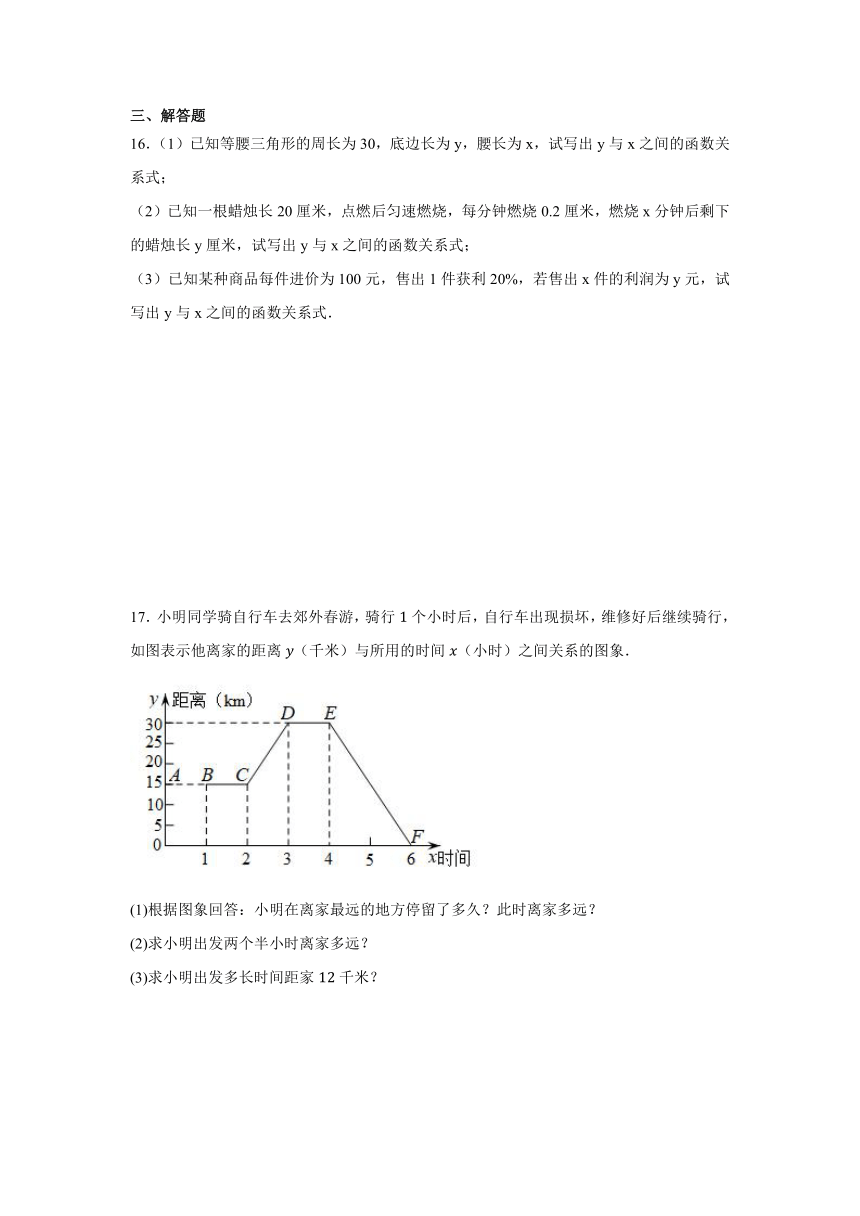
16.(1)已知等腰三角形的周长为30,底边长为y,腰长为x,试写出y与x之间的函数关系式;
(2)已知一根蜡烛长20厘米,点燃后匀速燃烧,每分钟燃烧0.2厘米,燃烧x分钟后剩下的蜡烛长y厘米,试写出y与x之间的函数关系式;
(3)已知某种商品每件进价为100元,售出1件获利20%,若售出x件的利润为y元,试写出y与x之间的函数关系式.
17.小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离(千米)与所用的时间(小时)之间关系的图象.
(1)根据图象回答:小明在离家最远的地方停留了多久?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家千米?
18.按如图所示的方式摆放餐桌和椅子,用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
(3)按如图所示的方式摆放餐桌和椅子,100张餐桌可以坐多少人?
(4)按如图所示的方式摆放餐桌和椅子,能否刚好坐80人?请说明理由.
19.下表是佳佳往朋友家打长途电话的几次收费记载:
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)你能帮佳佳预测一下,如果她打电话用时间是10分钟,则需付多少电话费
20.如图,是一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边两个点;第三层每边有三个点,依此类推:
(1)填写下表:
层数 1 2 3 4 5 6 ……
该层的点数 ……
所有层的点数 ……
(2)每层点数是如何随层数的变化而变化的?所有层的总点数是如何随层数的变化而变化的?
(3)此题中的自变量和因变量分别是什么?
(4)写出第n层所对应的点数,以及n层的六边形点阵的总点数;
(5)如果某一层的点数是96,它是第几层?
(6)有没有一层,它的点数是100?为什么?
参考答案
1.D
2.D
3.B
4.D
5.B
6.C
7.B
8.D
9. h,S
10. x,y -1,90
11.10cm
12.
13. y=23-0.007x 19.5 1000
14. h=25n+80; 8.
15. 300 4 6 200 3 5 100
16.(1)∵2x+y=30,
∴y=30-2x,即x<15,
∵两边之和大于第三边,即2x>y,
∴2x>(30-2x).
∴x>7.5,
综上可得;
(2)由题意,得y=20-0.2x.
∵,
∴20-0.2x≥0,
∴x≤100,
∴综上可得:.
(3)由题意得,每一件商品的利润为:,
所以,利润y=20x.
∴(,且x为整数)
17.(1)根据图象,小明在离家最远的地方停留了小时,此时离家千米.
(2)段表示的速度为千米/时,
(千米).
即小明出发两个半小时离家千米.
(3)段表示的速度为(千米/时),
(小时),
段表示的速度为(千米/时),
(小时),
即当小明出发小时与小时时,小明距家千米.
18.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x-1)=4x+2个座位.
故可坐人数y=4x+2,
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
(3)由(2)可得y=4x+2,
把x=100代入y=4x+2,
得y=4×100+2=402.
答:100张餐桌可以坐402人.
(4)不能刚好坐80人.理由如下:
把y=80代入y=4x+2,得
4x+2=80,解得x=.
∵人数是整数,
∴不能刚好坐80人.
19.(1)通话时间与电话费;其中通话时间是自变量,电话费是因变量;
(2)设时间为x,电话费为y,则有y=0.6x,
∴当x=10时,y=6元.
20.(1)如表:
层数 1 2 3 4 5 6
该层对应的点数 1 6 12 18 24 30
所有层的总点数 1 7 19 37 61 91
(2)每层点数是随层数增加而增加,所有层的总点数是随层数的增加而增加;
(3)自变量是层数,因变量是点数;
(4)第一层上的点数为1;
第二层上的点数为6=1×6;
第三层上的点数为6+6=2×6;
第四层上的点数为6+6+6=3×6;
…
第n层上的点数为(n-1)×6=6n-6.
所以n层六边形点阵的总点数为:
1+1×6+2×6+3×6+…+(n-1)×6
=1+6[1+2+3+4+…+(n-1)]=1+6[(1+2+3+…+n-1)+(n-1+n-2+…+3+2+1)]÷2
=1+6×=1+3n(n-1);
(5)第n层有(6n-6)个点,
则有6n-6=96,
解得n=17,
即在第17层;
(6)6n-6=100
解得n=,不合题意,所以没有一层,它的点数为100点.
一、单选题
1.关于变量x,y有如下关系:①x-y=5;②y2=2x;③:y=|x|;④y=.其中y是x函数的是( )
A. B. C. D.
2.函数 中,自变量x的取值范围是( )
A.x≠0 B.x<1 C.x>1 D.x≠1
3.圆周长公式C=2πR中,下列说法正确的是( )
A.π、R是变量,2为常量 B.C、R为变量,2、π为常量
C.R为变量,2、π、C为常量 D.C为变量,2、π、R为常量
4.如图,用每张长为的纸片,重叠粘贴成一条纸带,则纸带的长度与纸片的张数x之间的函数关系式是( )
A. B. C. D.
5.汽车油箱中有汽油,如果不再加油,油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为.当时,y与x之间的关系式是( )
A. B.
C. D.
6.小明骑自行车上学,一开始以某一恒定的速度行驶,但行驶至途中自行车发生了故障,只好停下来修车,车修好后,因怕耽误了上课,他比修车前加快了骑车的速度,下面四幅图中最能反映小明这段行程的是( )
A. B.
C. D.
7.甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是
A.甲、乙两人的速度相同 B.甲先到达终点
C.乙用的时间短 D.乙比甲跑的路程多
8.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
二、填空题
9.三角形的面积公式S=ah中,若底边a保持不变,则常量是 ,变量是 .
10.直角三角形两锐角的度数分别为,,其关系式为,其中变量为 ,常量为 .
11.弹簧的长度与所挂物体的质量的关系如图所示,由图可知不挂重物时弹簧的长为 .
12.长方形的周长为20,宽为x.若设长方形的面积为S,则面积S与宽x之间的关系是 .
13.夏天高山上的气温从山脚起每升高l00m降低0.7℃,已知山脚下的气温是23℃,则气温y(℃)与上升的高度x(m)之间的关系式为 ;当x=500时,y= ;当y=16时,x= .
14.一种树苗栽种时的高度为80cm,为研究它们的生长情况,测得数据如表;
栽种以后的年数n/年 1 2 3 4 …
高度h/m 105 130 155 180 …
则按照表中呈现的规律,树苗的高度h与栽种年数n的关系式为 ,栽种 年后,树苗能长到280cm.
15.星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题:
(1)公共阅报栏离小红家有__________米,小红从家走到公共阅报栏用了__________分;
(2)小红在公共阅报栏看新闻一共用了__________分;
(3)邮亭离公共阅报栏有__________米,小红从公共阅报栏到邮亭用了__________分;
(4)小红从邮亭走回家用了__________分,平均速度是__________米/分.
三、解答题
16.(1)已知等腰三角形的周长为30,底边长为y,腰长为x,试写出y与x之间的函数关系式;
(2)已知一根蜡烛长20厘米,点燃后匀速燃烧,每分钟燃烧0.2厘米,燃烧x分钟后剩下的蜡烛长y厘米,试写出y与x之间的函数关系式;
(3)已知某种商品每件进价为100元,售出1件获利20%,若售出x件的利润为y元,试写出y与x之间的函数关系式.
17.小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离(千米)与所用的时间(小时)之间关系的图象.
(1)根据图象回答:小明在离家最远的地方停留了多久?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家千米?
18.按如图所示的方式摆放餐桌和椅子,用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
(3)按如图所示的方式摆放餐桌和椅子,100张餐桌可以坐多少人?
(4)按如图所示的方式摆放餐桌和椅子,能否刚好坐80人?请说明理由.
19.下表是佳佳往朋友家打长途电话的几次收费记载:
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)你能帮佳佳预测一下,如果她打电话用时间是10分钟,则需付多少电话费
20.如图,是一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边两个点;第三层每边有三个点,依此类推:
(1)填写下表:
层数 1 2 3 4 5 6 ……
该层的点数 ……
所有层的点数 ……
(2)每层点数是如何随层数的变化而变化的?所有层的总点数是如何随层数的变化而变化的?
(3)此题中的自变量和因变量分别是什么?
(4)写出第n层所对应的点数,以及n层的六边形点阵的总点数;
(5)如果某一层的点数是96,它是第几层?
(6)有没有一层,它的点数是100?为什么?
参考答案
1.D
2.D
3.B
4.D
5.B
6.C
7.B
8.D
9. h,S
10. x,y -1,90
11.10cm
12.
13. y=23-0.007x 19.5 1000
14. h=25n+80; 8.
15. 300 4 6 200 3 5 100
16.(1)∵2x+y=30,
∴y=30-2x,即x<15,
∵两边之和大于第三边,即2x>y,
∴2x>(30-2x).
∴x>7.5,
综上可得;
(2)由题意,得y=20-0.2x.
∵,
∴20-0.2x≥0,
∴x≤100,
∴综上可得:.
(3)由题意得,每一件商品的利润为:,
所以,利润y=20x.
∴(,且x为整数)
17.(1)根据图象,小明在离家最远的地方停留了小时,此时离家千米.
(2)段表示的速度为千米/时,
(千米).
即小明出发两个半小时离家千米.
(3)段表示的速度为(千米/时),
(小时),
段表示的速度为(千米/时),
(小时),
即当小明出发小时与小时时,小明距家千米.
18.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x-1)=4x+2个座位.
故可坐人数y=4x+2,
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
(3)由(2)可得y=4x+2,
把x=100代入y=4x+2,
得y=4×100+2=402.
答:100张餐桌可以坐402人.
(4)不能刚好坐80人.理由如下:
把y=80代入y=4x+2,得
4x+2=80,解得x=.
∵人数是整数,
∴不能刚好坐80人.
19.(1)通话时间与电话费;其中通话时间是自变量,电话费是因变量;
(2)设时间为x,电话费为y,则有y=0.6x,
∴当x=10时,y=6元.
20.(1)如表:
层数 1 2 3 4 5 6
该层对应的点数 1 6 12 18 24 30
所有层的总点数 1 7 19 37 61 91
(2)每层点数是随层数增加而增加,所有层的总点数是随层数的增加而增加;
(3)自变量是层数,因变量是点数;
(4)第一层上的点数为1;
第二层上的点数为6=1×6;
第三层上的点数为6+6=2×6;
第四层上的点数为6+6+6=3×6;
…
第n层上的点数为(n-1)×6=6n-6.
所以n层六边形点阵的总点数为:
1+1×6+2×6+3×6+…+(n-1)×6
=1+6[1+2+3+4+…+(n-1)]=1+6[(1+2+3+…+n-1)+(n-1+n-2+…+3+2+1)]÷2
=1+6×=1+3n(n-1);
(5)第n层有(6n-6)个点,
则有6n-6=96,
解得n=17,
即在第17层;
(6)6n-6=100
解得n=,不合题意,所以没有一层,它的点数为100点.
