2025年九年级中考数学三轮冲刺练习反比例函数等腰三角形存在性问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习反比例函数等腰三角形存在性问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:04:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习反比例函数等腰三角形存在性问题
1.如图,在平面直角坐标系中,点A、B分别在函数y(x>0)、y,k为常数)的图象上,AB⊥x轴,垂足为C,OC=4,AB=7.
(1)求k的值;
(2)当点P在函数y(x>0)的图象上,且S△POC=8,求点P的坐标;
(3)在(2)的条件下,如果x轴上有一点Q,使得△POQ是等腰三角形,请直接写出所有满足条件的点Q的坐标.
2.如图,正比例函数y=k1x图象与反比例函数图象交于点A(4,3),直线BC∥OA,交y轴于点B,x轴于点D,交双曲线于点C,C点横坐标为8,连接AC,AB.
(1)求正比例函数,反比例函数解析式;
(2)求△ABC的面积.
(3)点P是y轴上一点,使得以点P、B、D为顶点的三角形是等腰三角形;请直接写出点P坐标.
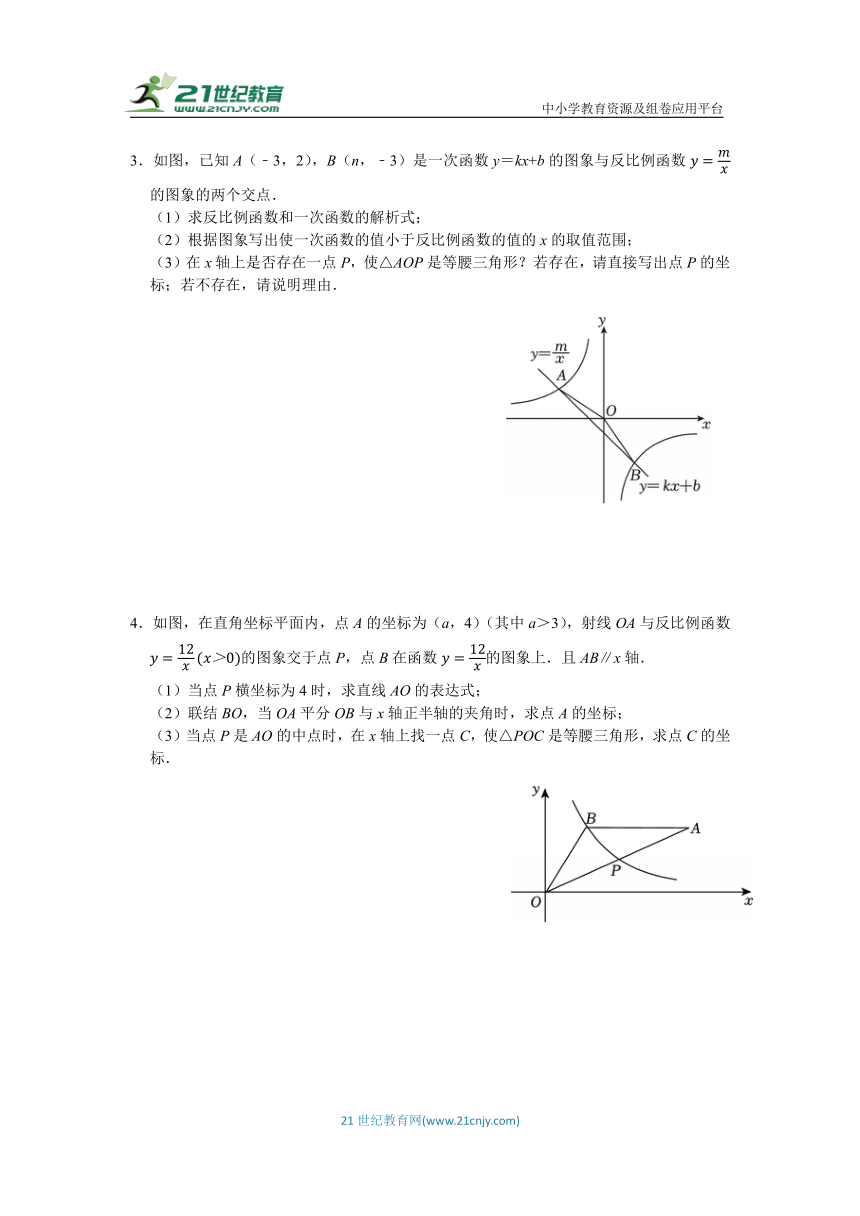
3.如图,已知A(﹣3,2),B(n,﹣3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)在x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
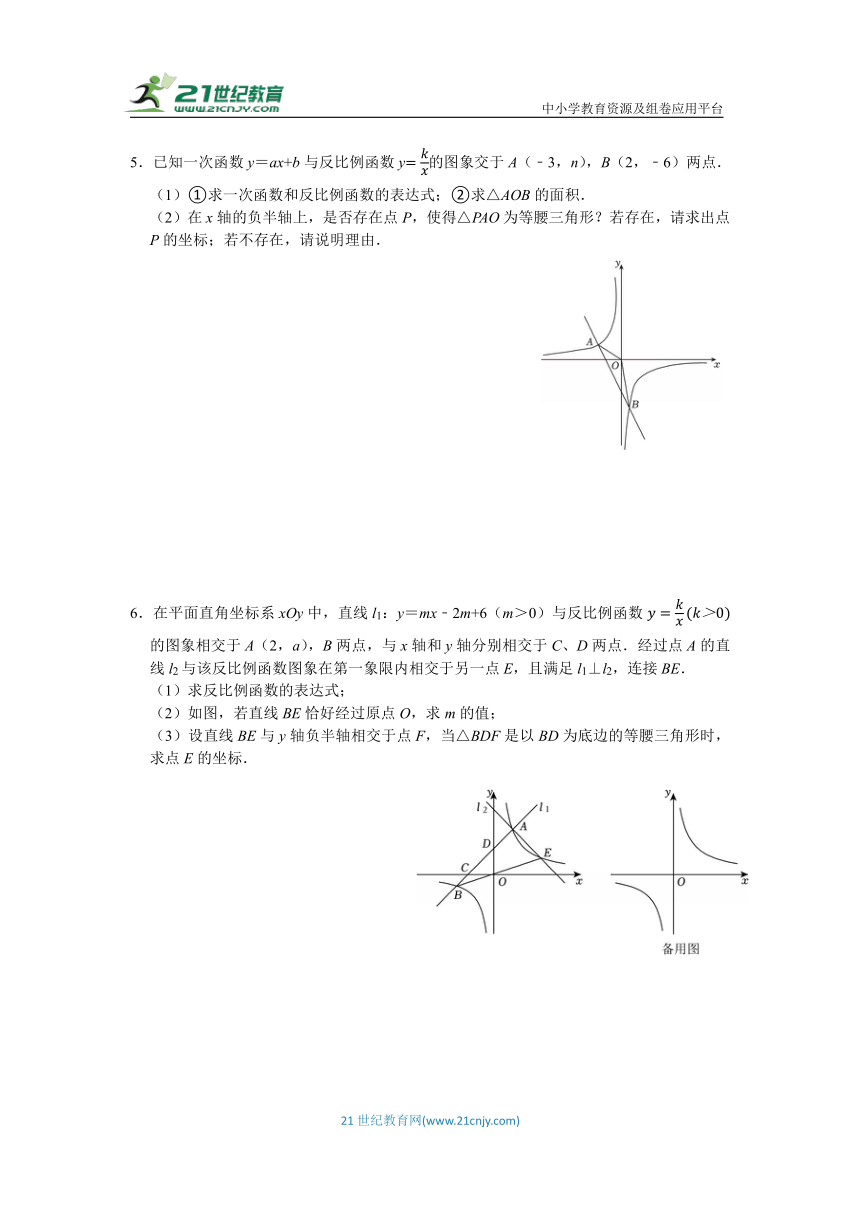
4.如图,在直角坐标平面内,点A的坐标为(a,4)(其中a>3),射线OA与反比例函数的图象交于点P,点B在函数的图象上.且AB∥x轴.
(1)当点P横坐标为4时,求直线AO的表达式;
(2)联结BO,当OA平分OB与x轴正半轴的夹角时,求点A的坐标;
(3)当点P是AO的中点时,在x轴上找一点C,使△POC是等腰三角形,求点C的坐标.
5.已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点.
(1)①求一次函数和反比例函数的表达式;②求△AOB的面积.
(2)在x轴的负半轴上,是否存在点P,使得△PAO为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
6.在平面直角坐标系xOy中,直线l1:y=mx﹣2m+6(m>0)与反比例函数的图象相交于A(2,a),B两点,与x轴和y轴分别相交于C、D两点.经过点A的直线l2与该反比例函数图象在第一象限内相交于另一点E,且满足l1⊥l2,连接BE.
(1)求反比例函数的表达式;
(2)如图,若直线BE恰好经过原点O,求m的值;
(3)设直线BE与y轴负半轴相交于点F,当△BDF是以BD为底边的等腰三角形时,求点E的坐标.
7.如图所示,反比例函数y(m≠0)的图象与一次函数y=kx+b(k≠0)的图象交于A(2,a+2)、B(a﹣10,﹣1)两点,直线AB分别与x轴、y轴交于点C、D.
(1)分别求反比例函数和一次函数的解析式;
(2)若P(t,0)(t≠2)是x轴的正半轴上一动点,过P作x轴的垂线,分别与一次函数的图象和反比例函数的图象交于点M、N,设MN的长为d,求出d与t之间的函数关系式;
(3)在第二象限内是否存在点Q,使得△CDQ是等腰直角三角形.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
8.如图,在直角坐标平面内,一个正比例函数y=kx的图象与反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
(1)求正比例函数的解析式;
(2)在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;
(3)已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.
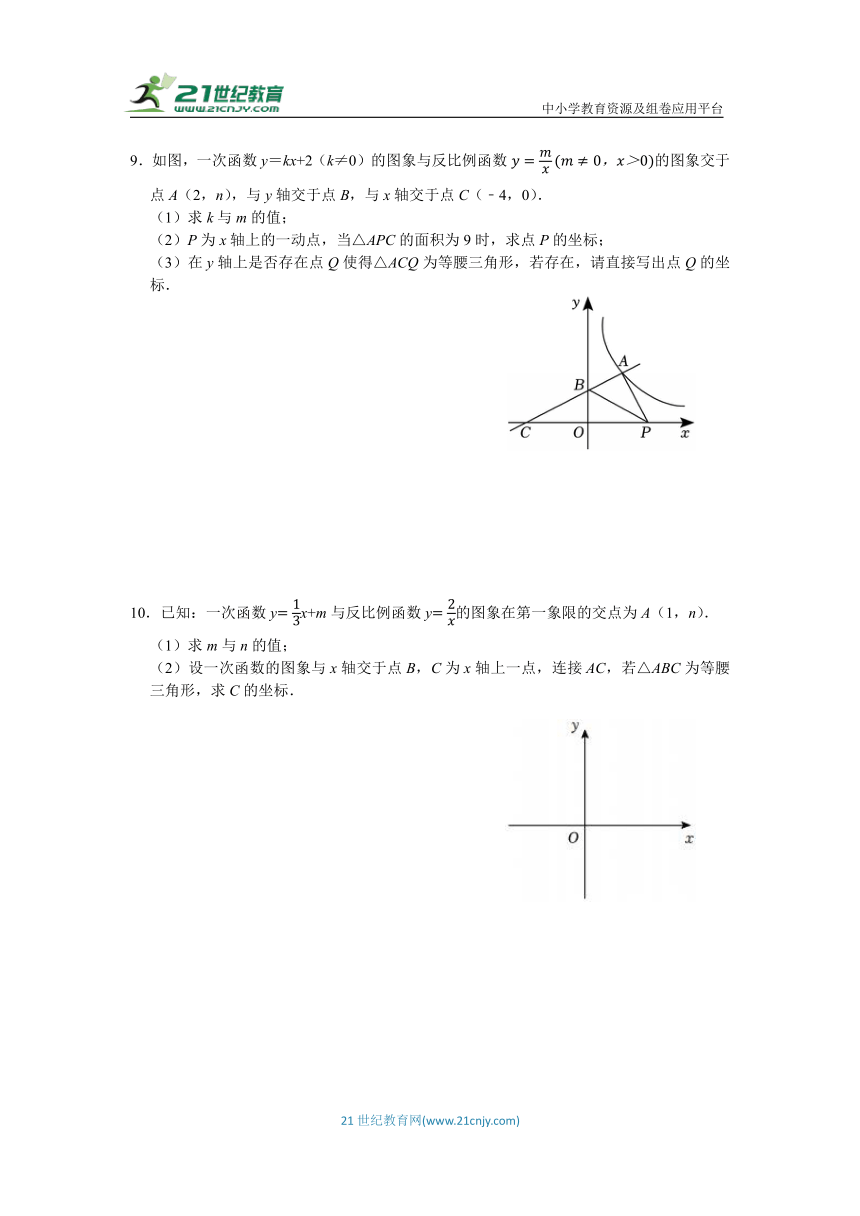
9.如图,一次函数y=kx+2(k≠0)的图象与反比例函数的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P为x轴上的一动点,当△APC的面积为9时,求点P的坐标;
(3)在y轴上是否存在点Q使得△ACQ为等腰三角形,若存在,请直接写出点Q的坐标.
10.已知:一次函数yx+m与反比例函数y的图象在第一象限的交点为A(1,n).
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,C为x轴上一点,连接AC,若△ABC为等腰三角形,求C的坐标.
11.如图,在平面直角坐标系中,一次函数y=k1x+b(k1≠0)的图象与反比例函数y(k2≠0)的图象相交于点A(2,4),B(﹣4,m)两点.
(1)分别求出一次函数和反比例函数的解析式;
(2)点P是反比例函数右下支上的动点,且△ABP 为等腰三角形,求出所有满足条件的P点.
12.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n)
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
13.如图,直线y=﹣x+2与反比例函数的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线AB上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,直接写出M点的坐标;若不存在,说明理由.
14.如图,一次函数y=k1x+b(k1≠0)与反比例函数的图象交于点A(2,3),B(a,﹣1),设直线AB交x轴于点C.
(1)求反比例函数和一次函数的解析式.
(2)直接写出的解集.
(3)若点P是反比例函数图象上的一点,且△POC是以OC为底边的等腰三角形,求P点的坐标.
15.如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4,cos∠ACH.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.
参考答案
1.【解答】解:(1)当x=4时,y2,y,
即点A、B的坐标分别为:(4,2)、(4,),
则AB=7=2,则k=﹣20;
(2)设点P(x,),
则S△POCOC×|yP|8,
解得:x=5,
则点P(5,﹣4);
(3)设点Q(x,0),
由点O、P、Q的坐标得,PO2=14,OQ2=x2,PQ2=(x﹣5)2+16,
当OP=OQ时,即14=x2,则x=±,
则点Q(,0)或(,0);
当OP=PQ或OQ=PQ时,则x2=(x﹣5)2+16或(x﹣5)2+16=41,
则x=4.1或10(不合题意的根已经舍去),
则点Q(10,0)或(4.1,0),
综上,Q(,0)或(,0)或(10,0)或(4.1,0).
2.【解答】解:(1)∵正比例函数y=k1x的图象过点A(4,3),
∴4k1=3,
解得k1,
∴正比例函数的解析式为yx,
∵反比例函数图象过点A(4,3),
∴3,
解得:k2=12,
∴反比例函数的解析式为y;
(2)连接OC,如图,
∵C点横坐标为8,
∴当x=8时,y,
∴C(8,),
∵OA∥BC,
∴设直线BC的解析式为yx+n,
∴8+n,
∴n,
∴直线BC的解析式为yx,
∴B(0,),
∴OB,
∵OA∥BC,
∴S△OAC=S△OAB,
∴S△ABC=S△OBCOB xC8=18;
(3)在yx中,令y=0,则x=6,
∴D(6,0),
∴BD,
①当DP=DB时,设P(0,y),
∵OD⊥BP,
∴OP=OB,
∴y,
∴P(0,);
②当BP=DB时,
∴OP=BP﹣OB3或OP=BP+OB=12,
∴P(0,﹣12)或P(0,3);
③当PB=PD时,则(y)2=62+y2,
解得y,
∴P(0,);
综上所述.满足条件的点P的坐标为(0,)或(0,﹣12)或P(0,3)或(0,).
3.【解答】解:(1)将A(﹣3,2)代入得:m=﹣6,
∴反比例函数的解析式是,
将B(n,﹣3)代入得:n=2,
∴B的坐标为B(2,﹣3),
将A(﹣3,2),B(2,﹣3)代入y=kx+b得:
,
∴,
∴一次函数的解析式为y=﹣x﹣1;
(2)根据图像,结合题意,得:﹣3<x<0或x>2;
(3)存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0);理由如下:
如图2,
在x轴上存在点P,使△AOP 是等腰三角形由A(﹣3,2)可得:OA,
当△AOP是等腰三角形时,分三种情况讨论:
①当AO=AP时(图2中P1),作AS⊥x轴于点S,由A(﹣3,2),等腰三角形三线合一的性质得:OS=P1S=3,由AS=2,OS=3,
∴P1O=6,
故P1(﹣6,0);
②当AO=PO时(图2中P2),P点在O点左侧时,P2(,0);
P点在O点右侧时,P3(,0);
③当PA=PO时(AP'=P'O)时,即AP'2=P'O2,
∴22+(3﹣OP')2=OP'2,
∴OP',
∴P'(,0),
综上所述,存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0).
4.【解答】解:(1)∵点P横坐标为4,
∴点P横坐标为:y3,
∴P(4,3),
设直线AO的解析式为y=kx,
代入P(4,3),得3=4k,
解得k,
∴直线AO的解析式为yx;
(2)∵点A的坐标为(a,4)(其中a>3),AB∥x轴,
∴B点纵坐标为4,
当y=4时,x=3,
∴B(3,4),
∴OB5,
∵OA平分OB与x轴正半轴的夹角,
∴∠AOB=∠1,
∵AB∥x轴,
∴∠1=∠OAB,
∴∠AOB=∠OAB,
∴AB=OB=5,
∴A(9,4);
(3)如图,过A作AE⊥x轴于E,过P作PF⊥x轴于F,
∴PF∥AE,
∵点P是AO的中点,
∴AP=OP,
∴OF=EF,
∴PF,
∵点A的坐标为(a,4),
∴AE=4,
∴PF=2,
把y=2代得x=6,
∴P(6,2),
∴OP2,
∵△POC是等腰三角形,
∴①OP=OC=2时,△POC是等腰三角形,
∴C(﹣2,0)或(2,0);
②OP=CC=2时,△POC是等腰三角形,
∴OC=2OF=12,
∴C(12,0);
③当OC=PC时,△POC是等腰三角形,如图,
此时,点在OP的垂直平分线上,
设C(m,0),
∴OC=PC=m,
∴CF=6﹣m,
在Rt△PCF中,PC2=PF2+CF2,
∴m2=(6﹣m)2+22,
∴m,
∴C(,0),
综上所述,点C的坐标为(﹣2,0)或(2,0)或C(12,0)或(,0).
5.【解答】解:(1)①已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点,将点B的坐标代入y= 得:
﹣6= ,
解得:k=﹣12;
∴反比例函数的表达式为y= ;
将点A的坐标代入y= 得:
,
∴A(﹣3,4);
将点A,点B的坐标代入得:
,
解得:,
∴一次函数的表达式为:y=﹣2x﹣2
②设一次函数y=﹣2x﹣2与x轴交于点C,如图:
由0=﹣2x﹣2得x=﹣1;
∴C(﹣1,0),
∴;
(2)在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;理由如下:
设点P(p,0)(p<0),
①PA=PO,则,
解得:;
②AP=AO,则,
解得:p=﹣6或p=0(不合题意,舍去);
③OP=OA,则,
解得:p=﹣5;
综上所述,在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;点P的坐标为或(﹣6,0)或(﹣5,0).
6.【解答】解:(1)当x=2时,直线l1:y=mx﹣2m+6=6,
∴A(2,6),
∵点A在反比例函数图象上,
∴k=2×6=12,
∴反比例函数的表达式为y;
(2)∵l1⊥l2,
∴设直线l2:yx+b,
把A(2,6)代入得,62+b,
解得b6,
∴直线l2:yx6,
解得,,
∴E(6m,),
解得,,
∴,
设直线BE的解析式为y=cx,
∴,
解得m=±1,
∵m>0,
∴m=1.
方法二:过点A作MN∥x轴,过点B作BM⊥MN 于点M,过点E作 EN⊥MN 于点N.
∵∠M=∠N=∠BAE=90°,
∴∠BAM+∠EAN=∠BAM+∠ABM=90°,
∴∠ABM=∠EAN,
∴△BMA∽△ANE,
∴,
设,
∵直线BE过原点,且点B和点E在反比例函数图象上,
∴,
∴,整理,得,
即,
解得n1=6,n2=﹣6(舍去),
∴点B的坐标为(﹣6,﹣2),
将 B(﹣6,﹣2)代入 y=mx﹣2m+6,得﹣6m﹣2m+6=﹣2,
∴m=1.
(3)方法一:由(2)知B(,﹣2m),E(6m,),
设直线BE解析式为y=k'x+b',
将点B和点E代入得,
,
解得,
∴直线BE的解析式为yx,
∴F(0,),
由直线l1的解析式为y=mx﹣2m+6,可得D(0,﹣2m+6),
∴DF2=(﹣2m+62m)2=(6)2,
BF2=(0)2+(﹣2m2m)2,
∵△BDF是以BD为底边的等腰三角形,
∴DF=BF,即(6)2,
整理得3m2﹣2m+3=0,
解得m,
∵m>0,
∴E(2+2,).
方法二:∵△BDF 为等腰三角形,且BD 为底边,
∴∠CDO=∠ABE,
∵∠COD=∠BAE=90°,
∴△CDO∽△EAB,
∴,即,
∵lAB:y=mx﹣2m+6,
∴,D(0,﹣2m+6),
∴,即,
联立整理,得mx2+(﹣2m+6)x﹣12=0,
解得,x2=2(舍去),
∴点B的坐标为,
∵AB⊥AE,
∴kAB kAE=﹣1,
∴,
设,
将点A(2,6)代入,得,
联立,
整理,得,
解得x1=6m,x2=2(舍去),
∴点E的坐标为,
过点A作 GH∥x轴,过点B作 BG⊥GH于点G,过点E作 EH⊥GH 于点H.
∵∠G=∠H=∠BAE=90°,
∴∠BAG+∠EAH=∠BAG+∠ABG=90°,
∴∠ABG=∠EAH,
∴△BGA∽△AHE,
∴,
∵A(2,6),,,
∴BG=6+2m,AH=6m﹣2,
∴,
解得:,(舍去).
∴点E的坐标为.
方法三:由(2)知B(,﹣2m),E(6m,),
∴KBE,
∴tanα=m,tanθ,tanβ,
∵α=β+θ,
∴tanα=tan(β+θ)m,
∴m,
整理得3m2﹣2m﹣3=0,
解得m,
∵m>0,
∴E(2+2,).
7.【解答】解:(1)∵反比例函数y(m≠0)的图象经过A(2,a+2)、B(a﹣10,﹣1)两点,
∴,
解得:,
∴A(2,4)、B(﹣8,﹣1),反比例函数的解析式是y,
把A(2,4)、B(﹣8,﹣1)分别代入y=kx+b得,,
解得,,
∴一次函数的解析式为yx+3;
(2)由题意得,M(t,t+3),N(t,),
∴PMt+3,PN,
当t>2时,d=PM﹣PNt+3;
当0<t≤2时,d=PN﹣PM(t+3);
(3)由(1)知,直线AB的解析式为yx+3,
令x=0,则yx+3=3,
令y=0,则0x+3,
∴x=﹣6,
∴C(﹣6,0),D(0,3),
∴OC=6,OD=3,如图,
∵△CDQ是等腰直角三角形,
∴①当∠CDQ=90°时,CD=QD,
过点Q作QH⊥y轴于H,
∴∠QDH+∠DQH=90°,
∵∠CDQ=90°,
∴∠QDH+∠CDO=90°,
∴∠CDO=∠DQH,
∴△COD≌△HDQ(AAS),
∴QH=OD=3,DH=OC=6,
∴OH=OD+DH=9,
∴Q(﹣3,9);
②当∠DCQ=90°时,同①的方法得,Q'(﹣9,6);
③当∠CQD=90°时,
同①的方法得,△CLQ''≌△DKQ'',
∴Q''L=Q''K,CL=DK,
∴设Q''(﹣a,a),
∴Q''K=Q''K=a,
∴CL=6﹣a,DK=a﹣3,
∴6﹣a=3﹣a,
∴a,
∴Q''(,),
即满足条件的点Q的坐标为(﹣3,9)或(﹣9,6)或(,).
8.【解答】解:(1)∵AB=3,
∴点A的纵坐标为3,
∵反比例函数y的图象经过点A,
当y=3时,x,
∴A(,3),
将点A(,3)代入y=kx得k,
∴正比例函数的解析式为yx;
(2)∵AB⊥x轴于点B,设点C的坐标为(,y),
在Rt△ABO中,OB,AB=3,
由勾股定理可得OA=2,
∵OB,
∴∠OAB=30°,
过点C作CG⊥OA于G,
由题意得CB=CG,
当点C在AB上时,
则OC平分∠AOB,
∴∠BOC=30°,
∴BCOB=1,
∴C(,1);
当点C在AB延长线上时,
同理可得C'(,﹣3);
综上所述:C(,1)或(,﹣3);
(3)①当AO=AP=2时,
则P(,3﹣2)或(,3+2);
②当OA=OP时,
由OB⊥AP得,AB=BP,
∴P(,﹣3);
③当PA=PO时,
∴∠OAP=∠POA=30°,
则OP平分∠AOB,
∴P(,1);
综上所述:P(,3﹣2)或(,3+2)或(,1)或(,﹣3).
9.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k.把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入得:m=2×3=6.
∴k的值为,m的值为6;
(2)设点P(x,0),
则△APC的面积CP×yA|x+4|×3=9,
解得:x=2或﹣10,
即点P(2,0)或(﹣10,0);
(3)存在,理由:
设点Q(0,y),
由点A、C、Q的坐标得,AC2=45,CQ2=16+y2,AQ2=4+(y﹣3)2,
当CA=CQ时,
则45=16+y2,则y=±,
则点P(0,)或(0,);
当AC=AQ或CQ=AQ时,
同理可得:16+y2=4+(y﹣3)2或45=4+(y﹣3)2,
解得:y或3±,
则点P(0,)或(0,3)或(0,3).
综上,P(0,)或(0,)或(0,)或(0,3)或(0,3).
10.【解答】解:(1)∵A(1,n)在反比例数的图象上,
∴,
∴n=2,
∴A(1,2),
将A(1,2)代入得:
,
解得:;
(2)由(1)得,
当y=0时,x=﹣5,
∵一次函数的图象与x轴交于点B,
∴B(﹣5,0),
∴,
如图所示,设C(x,0),
当BC=BA时,点C的坐标为或;
当CB=CA时,得:CB2=CA2,
∴(x+5)2=(1﹣x)2+22,
解得:;
当AB=AC时,
∵A(1,2),xA﹣xB=6,
∴C(7,0),
综上所述满足条件的点C坐标为或或或C(7,0).
11.【解答】解:(1)将A(2,4),代入y,
∴k2=2×4=8,
∴y,
将B(﹣4,m)代入y,则m=﹣2,
∴B(﹣4,﹣2),
将A(2,4),B(﹣4,﹣2)代入y=k1x+b(k1≠0),
∴,解得:,
∴y=x+2.
(2)∵点P是反比例函数右支下方x轴上的动点,
设P(p,0),p>0,
∵A(2,4),B(﹣4,﹣2),
∴PA2=(p﹣2)2+42,PB2=(p+4)2+22,AB2=(2+4)2+(4+2)2=72,
∵△ABP为等腰三角形,
①当AB=AP时,(p﹣2)2+42=72,
解得:p=2(舍去)或p=2,
∴点P的坐标为:(2,0),
②当BP=BA时,(p+4)2+22=72,
解得:p=﹣24(舍去)或p=24,
∴点P的坐标为(24,0),
③当PB=PA时,(p+4)2+22=(p﹣2)2+42,
解得:p=0(舍去).
综上所述,P(2,0)或(24,0).
12.【解答】解:(1)AO=5,OD:AD=3:4,
设:OD=3a,AD=4a,则AD=5a=5,解得:a=1,
故点A(3,4),
则m=3×4=12,
故反比例函数的表达式为:y,故B(﹣6,﹣2),
将点A、B的坐标代入一次函数表达式y=kx+b得:,解得:,
故一次函数的表达式为:yx+2;
(2)设一次函数交y轴于点M(0,2),
△AOB的面积SOM×(xA﹣xB)2×(3+6)=9;
(3)设点P(0,m),而点A、O的坐标分别为:(3,4)、(0,0),
AP2=9+(m﹣4)2,AO2=25,PO2=m2,
当AP=AO时,9+(m﹣4)2=25,解得:m=8或0(舍去0);
当AO=PO时,同理可得:m=±5;
当AP=PO时,同理可得:m;
综上,P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,).
13.【解答】解:(1)∵直线y=﹣x+2与反比例函数的图象交A(a,3),B(3,b)两点,
∴﹣a+2=3,﹣3+2=b,
∴a=﹣1,b=﹣1,
∴A(﹣1,3),B(3,﹣1),
∵点A(﹣1,3)在反比例函数图象上,
∴k=﹣1×3=﹣3,
∴反比例函数解析式为;
(2)连接CP、PD,作PE⊥AC,垂足为E,PF⊥BD,垂足为F,
设P(x0,﹣x0+2),
∵A(﹣1,3),
∴C(﹣1,0),
∵B(3,﹣1),
∴D(3,0),
∴,.
∵S△ACP=S△BDP,
∴,
∴x0=0或x0=﹣3(不合题意,舍去),
∴P(0,2);
(3)在x轴正半轴上存在点M,使得△MAB为等腰三角形;或.理由如下:
设M(m,0)(m>0),
∵A(﹣1,3),B(3,﹣1),
∴MA2=(m+1)2+9,MB2=(m﹣3)2+1,AB2=(3+1)2+(﹣1﹣3)2=32,
∵△MAB是等腰三角形,
∴①当MA=MB时,(m+1)2+9=(m﹣3)2+1,
∴m=0(舍去);
②当MA=AB时,(m+1)2+9=32,
∴或(舍去),
∴;
③当MB=AB时,(m﹣3)2+1=32,
∴或(舍去),
∴;
综上所述,在x轴正半轴上存在点M,使得△MAB为等腰三角形;满足条件的或.
14.【解答】解:(1)将点A(2,3)代入得,k2=2×3=6,
∴y,
将点B(a,﹣1)代入y得,a=﹣6,
∴B(﹣6,﹣1),
将点A(2,3),B(﹣6,﹣1)代入y=k1x+b得,
,
解得,
∴一次函数的解析式为yx+2;
(2)由图象知:当x<﹣6或0<x<2时,;
(3)当y=0时,x+2=0,
∴x=﹣4,
∴C(﹣4,0),
∵PC=PO,
∴点P在OC的垂直平分线上,
∴点P的横坐标为﹣2,
∴P(﹣2,﹣3).
15.【解答】解:(1)∵AC=4,cos∠ACH,
∴,
解得,CH=4,
由勾股定理得,AH8,
∵点O是线段CH的中点,
∴点A的坐标为(﹣2,8),点C的坐标为(2,0),
∴反比例函数的解析式为:y2,
,
解得,,
∴一次函数解析式为y1=﹣2x+4;
(2)设P点坐标为(m,0),
当点A为等腰三角形的顶点时,PH=CH=4,
则OP=6,
∴P点坐标为(﹣6,0);
当点C为等腰三角形的顶点时,PC=CA=4,
则OP=42或42,
∴P点坐标为(2﹣4,0)或(42,0);
当点P为AC垂直平分线与x轴的交点时,PA=PC,
则(2﹣m)2=(﹣2﹣m)2+82,
解得,m=﹣8,
∴P点坐标为(﹣8,0).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习反比例函数等腰三角形存在性问题
1.如图,在平面直角坐标系中,点A、B分别在函数y(x>0)、y,k为常数)的图象上,AB⊥x轴,垂足为C,OC=4,AB=7.
(1)求k的值;
(2)当点P在函数y(x>0)的图象上,且S△POC=8,求点P的坐标;
(3)在(2)的条件下,如果x轴上有一点Q,使得△POQ是等腰三角形,请直接写出所有满足条件的点Q的坐标.
2.如图,正比例函数y=k1x图象与反比例函数图象交于点A(4,3),直线BC∥OA,交y轴于点B,x轴于点D,交双曲线于点C,C点横坐标为8,连接AC,AB.
(1)求正比例函数,反比例函数解析式;
(2)求△ABC的面积.
(3)点P是y轴上一点,使得以点P、B、D为顶点的三角形是等腰三角形;请直接写出点P坐标.
3.如图,已知A(﹣3,2),B(n,﹣3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)在x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
4.如图,在直角坐标平面内,点A的坐标为(a,4)(其中a>3),射线OA与反比例函数的图象交于点P,点B在函数的图象上.且AB∥x轴.
(1)当点P横坐标为4时,求直线AO的表达式;
(2)联结BO,当OA平分OB与x轴正半轴的夹角时,求点A的坐标;
(3)当点P是AO的中点时,在x轴上找一点C,使△POC是等腰三角形,求点C的坐标.
5.已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点.
(1)①求一次函数和反比例函数的表达式;②求△AOB的面积.
(2)在x轴的负半轴上,是否存在点P,使得△PAO为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
6.在平面直角坐标系xOy中,直线l1:y=mx﹣2m+6(m>0)与反比例函数的图象相交于A(2,a),B两点,与x轴和y轴分别相交于C、D两点.经过点A的直线l2与该反比例函数图象在第一象限内相交于另一点E,且满足l1⊥l2,连接BE.
(1)求反比例函数的表达式;
(2)如图,若直线BE恰好经过原点O,求m的值;
(3)设直线BE与y轴负半轴相交于点F,当△BDF是以BD为底边的等腰三角形时,求点E的坐标.
7.如图所示,反比例函数y(m≠0)的图象与一次函数y=kx+b(k≠0)的图象交于A(2,a+2)、B(a﹣10,﹣1)两点,直线AB分别与x轴、y轴交于点C、D.
(1)分别求反比例函数和一次函数的解析式;
(2)若P(t,0)(t≠2)是x轴的正半轴上一动点,过P作x轴的垂线,分别与一次函数的图象和反比例函数的图象交于点M、N,设MN的长为d,求出d与t之间的函数关系式;
(3)在第二象限内是否存在点Q,使得△CDQ是等腰直角三角形.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
8.如图,在直角坐标平面内,一个正比例函数y=kx的图象与反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
(1)求正比例函数的解析式;
(2)在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;
(3)已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.
9.如图,一次函数y=kx+2(k≠0)的图象与反比例函数的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P为x轴上的一动点,当△APC的面积为9时,求点P的坐标;
(3)在y轴上是否存在点Q使得△ACQ为等腰三角形,若存在,请直接写出点Q的坐标.
10.已知:一次函数yx+m与反比例函数y的图象在第一象限的交点为A(1,n).
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,C为x轴上一点,连接AC,若△ABC为等腰三角形,求C的坐标.
11.如图,在平面直角坐标系中,一次函数y=k1x+b(k1≠0)的图象与反比例函数y(k2≠0)的图象相交于点A(2,4),B(﹣4,m)两点.
(1)分别求出一次函数和反比例函数的解析式;
(2)点P是反比例函数右下支上的动点,且△ABP 为等腰三角形,求出所有满足条件的P点.
12.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y(m≠0)的图象相交于A,B两点,过点A作AD⊥x轴于点D,AO=5,OD:AD=3:4,B点的坐标为(﹣6,n)
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
13.如图,直线y=﹣x+2与反比例函数的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线AB上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,直接写出M点的坐标;若不存在,说明理由.
14.如图,一次函数y=k1x+b(k1≠0)与反比例函数的图象交于点A(2,3),B(a,﹣1),设直线AB交x轴于点C.
(1)求反比例函数和一次函数的解析式.
(2)直接写出的解集.
(3)若点P是反比例函数图象上的一点,且△POC是以OC为底边的等腰三角形,求P点的坐标.
15.如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4,cos∠ACH.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.
参考答案
1.【解答】解:(1)当x=4时,y2,y,
即点A、B的坐标分别为:(4,2)、(4,),
则AB=7=2,则k=﹣20;
(2)设点P(x,),
则S△POCOC×|yP|8,
解得:x=5,
则点P(5,﹣4);
(3)设点Q(x,0),
由点O、P、Q的坐标得,PO2=14,OQ2=x2,PQ2=(x﹣5)2+16,
当OP=OQ时,即14=x2,则x=±,
则点Q(,0)或(,0);
当OP=PQ或OQ=PQ时,则x2=(x﹣5)2+16或(x﹣5)2+16=41,
则x=4.1或10(不合题意的根已经舍去),
则点Q(10,0)或(4.1,0),
综上,Q(,0)或(,0)或(10,0)或(4.1,0).
2.【解答】解:(1)∵正比例函数y=k1x的图象过点A(4,3),
∴4k1=3,
解得k1,
∴正比例函数的解析式为yx,
∵反比例函数图象过点A(4,3),
∴3,
解得:k2=12,
∴反比例函数的解析式为y;
(2)连接OC,如图,
∵C点横坐标为8,
∴当x=8时,y,
∴C(8,),
∵OA∥BC,
∴设直线BC的解析式为yx+n,
∴8+n,
∴n,
∴直线BC的解析式为yx,
∴B(0,),
∴OB,
∵OA∥BC,
∴S△OAC=S△OAB,
∴S△ABC=S△OBCOB xC8=18;
(3)在yx中,令y=0,则x=6,
∴D(6,0),
∴BD,
①当DP=DB时,设P(0,y),
∵OD⊥BP,
∴OP=OB,
∴y,
∴P(0,);
②当BP=DB时,
∴OP=BP﹣OB3或OP=BP+OB=12,
∴P(0,﹣12)或P(0,3);
③当PB=PD时,则(y)2=62+y2,
解得y,
∴P(0,);
综上所述.满足条件的点P的坐标为(0,)或(0,﹣12)或P(0,3)或(0,).
3.【解答】解:(1)将A(﹣3,2)代入得:m=﹣6,
∴反比例函数的解析式是,
将B(n,﹣3)代入得:n=2,
∴B的坐标为B(2,﹣3),
将A(﹣3,2),B(2,﹣3)代入y=kx+b得:
,
∴,
∴一次函数的解析式为y=﹣x﹣1;
(2)根据图像,结合题意,得:﹣3<x<0或x>2;
(3)存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0);理由如下:
如图2,
在x轴上存在点P,使△AOP 是等腰三角形由A(﹣3,2)可得:OA,
当△AOP是等腰三角形时,分三种情况讨论:
①当AO=AP时(图2中P1),作AS⊥x轴于点S,由A(﹣3,2),等腰三角形三线合一的性质得:OS=P1S=3,由AS=2,OS=3,
∴P1O=6,
故P1(﹣6,0);
②当AO=PO时(图2中P2),P点在O点左侧时,P2(,0);
P点在O点右侧时,P3(,0);
③当PA=PO时(AP'=P'O)时,即AP'2=P'O2,
∴22+(3﹣OP')2=OP'2,
∴OP',
∴P'(,0),
综上所述,存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0).
4.【解答】解:(1)∵点P横坐标为4,
∴点P横坐标为:y3,
∴P(4,3),
设直线AO的解析式为y=kx,
代入P(4,3),得3=4k,
解得k,
∴直线AO的解析式为yx;
(2)∵点A的坐标为(a,4)(其中a>3),AB∥x轴,
∴B点纵坐标为4,
当y=4时,x=3,
∴B(3,4),
∴OB5,
∵OA平分OB与x轴正半轴的夹角,
∴∠AOB=∠1,
∵AB∥x轴,
∴∠1=∠OAB,
∴∠AOB=∠OAB,
∴AB=OB=5,
∴A(9,4);
(3)如图,过A作AE⊥x轴于E,过P作PF⊥x轴于F,
∴PF∥AE,
∵点P是AO的中点,
∴AP=OP,
∴OF=EF,
∴PF,
∵点A的坐标为(a,4),
∴AE=4,
∴PF=2,
把y=2代得x=6,
∴P(6,2),
∴OP2,
∵△POC是等腰三角形,
∴①OP=OC=2时,△POC是等腰三角形,
∴C(﹣2,0)或(2,0);
②OP=CC=2时,△POC是等腰三角形,
∴OC=2OF=12,
∴C(12,0);
③当OC=PC时,△POC是等腰三角形,如图,
此时,点在OP的垂直平分线上,
设C(m,0),
∴OC=PC=m,
∴CF=6﹣m,
在Rt△PCF中,PC2=PF2+CF2,
∴m2=(6﹣m)2+22,
∴m,
∴C(,0),
综上所述,点C的坐标为(﹣2,0)或(2,0)或C(12,0)或(,0).
5.【解答】解:(1)①已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点,将点B的坐标代入y= 得:
﹣6= ,
解得:k=﹣12;
∴反比例函数的表达式为y= ;
将点A的坐标代入y= 得:
,
∴A(﹣3,4);
将点A,点B的坐标代入得:
,
解得:,
∴一次函数的表达式为:y=﹣2x﹣2
②设一次函数y=﹣2x﹣2与x轴交于点C,如图:
由0=﹣2x﹣2得x=﹣1;
∴C(﹣1,0),
∴;
(2)在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;理由如下:
设点P(p,0)(p<0),
①PA=PO,则,
解得:;
②AP=AO,则,
解得:p=﹣6或p=0(不合题意,舍去);
③OP=OA,则,
解得:p=﹣5;
综上所述,在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;点P的坐标为或(﹣6,0)或(﹣5,0).
6.【解答】解:(1)当x=2时,直线l1:y=mx﹣2m+6=6,
∴A(2,6),
∵点A在反比例函数图象上,
∴k=2×6=12,
∴反比例函数的表达式为y;
(2)∵l1⊥l2,
∴设直线l2:yx+b,
把A(2,6)代入得,62+b,
解得b6,
∴直线l2:yx6,
解得,,
∴E(6m,),
解得,,
∴,
设直线BE的解析式为y=cx,
∴,
解得m=±1,
∵m>0,
∴m=1.
方法二:过点A作MN∥x轴,过点B作BM⊥MN 于点M,过点E作 EN⊥MN 于点N.
∵∠M=∠N=∠BAE=90°,
∴∠BAM+∠EAN=∠BAM+∠ABM=90°,
∴∠ABM=∠EAN,
∴△BMA∽△ANE,
∴,
设,
∵直线BE过原点,且点B和点E在反比例函数图象上,
∴,
∴,整理,得,
即,
解得n1=6,n2=﹣6(舍去),
∴点B的坐标为(﹣6,﹣2),
将 B(﹣6,﹣2)代入 y=mx﹣2m+6,得﹣6m﹣2m+6=﹣2,
∴m=1.
(3)方法一:由(2)知B(,﹣2m),E(6m,),
设直线BE解析式为y=k'x+b',
将点B和点E代入得,
,
解得,
∴直线BE的解析式为yx,
∴F(0,),
由直线l1的解析式为y=mx﹣2m+6,可得D(0,﹣2m+6),
∴DF2=(﹣2m+62m)2=(6)2,
BF2=(0)2+(﹣2m2m)2,
∵△BDF是以BD为底边的等腰三角形,
∴DF=BF,即(6)2,
整理得3m2﹣2m+3=0,
解得m,
∵m>0,
∴E(2+2,).
方法二:∵△BDF 为等腰三角形,且BD 为底边,
∴∠CDO=∠ABE,
∵∠COD=∠BAE=90°,
∴△CDO∽△EAB,
∴,即,
∵lAB:y=mx﹣2m+6,
∴,D(0,﹣2m+6),
∴,即,
联立整理,得mx2+(﹣2m+6)x﹣12=0,
解得,x2=2(舍去),
∴点B的坐标为,
∵AB⊥AE,
∴kAB kAE=﹣1,
∴,
设,
将点A(2,6)代入,得,
联立,
整理,得,
解得x1=6m,x2=2(舍去),
∴点E的坐标为,
过点A作 GH∥x轴,过点B作 BG⊥GH于点G,过点E作 EH⊥GH 于点H.
∵∠G=∠H=∠BAE=90°,
∴∠BAG+∠EAH=∠BAG+∠ABG=90°,
∴∠ABG=∠EAH,
∴△BGA∽△AHE,
∴,
∵A(2,6),,,
∴BG=6+2m,AH=6m﹣2,
∴,
解得:,(舍去).
∴点E的坐标为.
方法三:由(2)知B(,﹣2m),E(6m,),
∴KBE,
∴tanα=m,tanθ,tanβ,
∵α=β+θ,
∴tanα=tan(β+θ)m,
∴m,
整理得3m2﹣2m﹣3=0,
解得m,
∵m>0,
∴E(2+2,).
7.【解答】解:(1)∵反比例函数y(m≠0)的图象经过A(2,a+2)、B(a﹣10,﹣1)两点,
∴,
解得:,
∴A(2,4)、B(﹣8,﹣1),反比例函数的解析式是y,
把A(2,4)、B(﹣8,﹣1)分别代入y=kx+b得,,
解得,,
∴一次函数的解析式为yx+3;
(2)由题意得,M(t,t+3),N(t,),
∴PMt+3,PN,
当t>2时,d=PM﹣PNt+3;
当0<t≤2时,d=PN﹣PM(t+3);
(3)由(1)知,直线AB的解析式为yx+3,
令x=0,则yx+3=3,
令y=0,则0x+3,
∴x=﹣6,
∴C(﹣6,0),D(0,3),
∴OC=6,OD=3,如图,
∵△CDQ是等腰直角三角形,
∴①当∠CDQ=90°时,CD=QD,
过点Q作QH⊥y轴于H,
∴∠QDH+∠DQH=90°,
∵∠CDQ=90°,
∴∠QDH+∠CDO=90°,
∴∠CDO=∠DQH,
∴△COD≌△HDQ(AAS),
∴QH=OD=3,DH=OC=6,
∴OH=OD+DH=9,
∴Q(﹣3,9);
②当∠DCQ=90°时,同①的方法得,Q'(﹣9,6);
③当∠CQD=90°时,
同①的方法得,△CLQ''≌△DKQ'',
∴Q''L=Q''K,CL=DK,
∴设Q''(﹣a,a),
∴Q''K=Q''K=a,
∴CL=6﹣a,DK=a﹣3,
∴6﹣a=3﹣a,
∴a,
∴Q''(,),
即满足条件的点Q的坐标为(﹣3,9)或(﹣9,6)或(,).
8.【解答】解:(1)∵AB=3,
∴点A的纵坐标为3,
∵反比例函数y的图象经过点A,
当y=3时,x,
∴A(,3),
将点A(,3)代入y=kx得k,
∴正比例函数的解析式为yx;
(2)∵AB⊥x轴于点B,设点C的坐标为(,y),
在Rt△ABO中,OB,AB=3,
由勾股定理可得OA=2,
∵OB,
∴∠OAB=30°,
过点C作CG⊥OA于G,
由题意得CB=CG,
当点C在AB上时,
则OC平分∠AOB,
∴∠BOC=30°,
∴BCOB=1,
∴C(,1);
当点C在AB延长线上时,
同理可得C'(,﹣3);
综上所述:C(,1)或(,﹣3);
(3)①当AO=AP=2时,
则P(,3﹣2)或(,3+2);
②当OA=OP时,
由OB⊥AP得,AB=BP,
∴P(,﹣3);
③当PA=PO时,
∴∠OAP=∠POA=30°,
则OP平分∠AOB,
∴P(,1);
综上所述:P(,3﹣2)或(,3+2)或(,1)或(,﹣3).
9.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k.把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入得:m=2×3=6.
∴k的值为,m的值为6;
(2)设点P(x,0),
则△APC的面积CP×yA|x+4|×3=9,
解得:x=2或﹣10,
即点P(2,0)或(﹣10,0);
(3)存在,理由:
设点Q(0,y),
由点A、C、Q的坐标得,AC2=45,CQ2=16+y2,AQ2=4+(y﹣3)2,
当CA=CQ时,
则45=16+y2,则y=±,
则点P(0,)或(0,);
当AC=AQ或CQ=AQ时,
同理可得:16+y2=4+(y﹣3)2或45=4+(y﹣3)2,
解得:y或3±,
则点P(0,)或(0,3)或(0,3).
综上,P(0,)或(0,)或(0,)或(0,3)或(0,3).
10.【解答】解:(1)∵A(1,n)在反比例数的图象上,
∴,
∴n=2,
∴A(1,2),
将A(1,2)代入得:
,
解得:;
(2)由(1)得,
当y=0时,x=﹣5,
∵一次函数的图象与x轴交于点B,
∴B(﹣5,0),
∴,
如图所示,设C(x,0),
当BC=BA时,点C的坐标为或;
当CB=CA时,得:CB2=CA2,
∴(x+5)2=(1﹣x)2+22,
解得:;
当AB=AC时,
∵A(1,2),xA﹣xB=6,
∴C(7,0),
综上所述满足条件的点C坐标为或或或C(7,0).
11.【解答】解:(1)将A(2,4),代入y,
∴k2=2×4=8,
∴y,
将B(﹣4,m)代入y,则m=﹣2,
∴B(﹣4,﹣2),
将A(2,4),B(﹣4,﹣2)代入y=k1x+b(k1≠0),
∴,解得:,
∴y=x+2.
(2)∵点P是反比例函数右支下方x轴上的动点,
设P(p,0),p>0,
∵A(2,4),B(﹣4,﹣2),
∴PA2=(p﹣2)2+42,PB2=(p+4)2+22,AB2=(2+4)2+(4+2)2=72,
∵△ABP为等腰三角形,
①当AB=AP时,(p﹣2)2+42=72,
解得:p=2(舍去)或p=2,
∴点P的坐标为:(2,0),
②当BP=BA时,(p+4)2+22=72,
解得:p=﹣24(舍去)或p=24,
∴点P的坐标为(24,0),
③当PB=PA时,(p+4)2+22=(p﹣2)2+42,
解得:p=0(舍去).
综上所述,P(2,0)或(24,0).
12.【解答】解:(1)AO=5,OD:AD=3:4,
设:OD=3a,AD=4a,则AD=5a=5,解得:a=1,
故点A(3,4),
则m=3×4=12,
故反比例函数的表达式为:y,故B(﹣6,﹣2),
将点A、B的坐标代入一次函数表达式y=kx+b得:,解得:,
故一次函数的表达式为:yx+2;
(2)设一次函数交y轴于点M(0,2),
△AOB的面积SOM×(xA﹣xB)2×(3+6)=9;
(3)设点P(0,m),而点A、O的坐标分别为:(3,4)、(0,0),
AP2=9+(m﹣4)2,AO2=25,PO2=m2,
当AP=AO时,9+(m﹣4)2=25,解得:m=8或0(舍去0);
当AO=PO时,同理可得:m=±5;
当AP=PO时,同理可得:m;
综上,P点坐标为:(0,8)或(0,5)或(0,﹣5)或(0,).
13.【解答】解:(1)∵直线y=﹣x+2与反比例函数的图象交A(a,3),B(3,b)两点,
∴﹣a+2=3,﹣3+2=b,
∴a=﹣1,b=﹣1,
∴A(﹣1,3),B(3,﹣1),
∵点A(﹣1,3)在反比例函数图象上,
∴k=﹣1×3=﹣3,
∴反比例函数解析式为;
(2)连接CP、PD,作PE⊥AC,垂足为E,PF⊥BD,垂足为F,
设P(x0,﹣x0+2),
∵A(﹣1,3),
∴C(﹣1,0),
∵B(3,﹣1),
∴D(3,0),
∴,.
∵S△ACP=S△BDP,
∴,
∴x0=0或x0=﹣3(不合题意,舍去),
∴P(0,2);
(3)在x轴正半轴上存在点M,使得△MAB为等腰三角形;或.理由如下:
设M(m,0)(m>0),
∵A(﹣1,3),B(3,﹣1),
∴MA2=(m+1)2+9,MB2=(m﹣3)2+1,AB2=(3+1)2+(﹣1﹣3)2=32,
∵△MAB是等腰三角形,
∴①当MA=MB时,(m+1)2+9=(m﹣3)2+1,
∴m=0(舍去);
②当MA=AB时,(m+1)2+9=32,
∴或(舍去),
∴;
③当MB=AB时,(m﹣3)2+1=32,
∴或(舍去),
∴;
综上所述,在x轴正半轴上存在点M,使得△MAB为等腰三角形;满足条件的或.
14.【解答】解:(1)将点A(2,3)代入得,k2=2×3=6,
∴y,
将点B(a,﹣1)代入y得,a=﹣6,
∴B(﹣6,﹣1),
将点A(2,3),B(﹣6,﹣1)代入y=k1x+b得,
,
解得,
∴一次函数的解析式为yx+2;
(2)由图象知:当x<﹣6或0<x<2时,;
(3)当y=0时,x+2=0,
∴x=﹣4,
∴C(﹣4,0),
∵PC=PO,
∴点P在OC的垂直平分线上,
∴点P的横坐标为﹣2,
∴P(﹣2,﹣3).
15.【解答】解:(1)∵AC=4,cos∠ACH,
∴,
解得,CH=4,
由勾股定理得,AH8,
∵点O是线段CH的中点,
∴点A的坐标为(﹣2,8),点C的坐标为(2,0),
∴反比例函数的解析式为:y2,
,
解得,,
∴一次函数解析式为y1=﹣2x+4;
(2)设P点坐标为(m,0),
当点A为等腰三角形的顶点时,PH=CH=4,
则OP=6,
∴P点坐标为(﹣6,0);
当点C为等腰三角形的顶点时,PC=CA=4,
则OP=42或42,
∴P点坐标为(2﹣4,0)或(42,0);
当点P为AC垂直平分线与x轴的交点时,PA=PC,
则(2﹣m)2=(﹣2﹣m)2+82,
解得,m=﹣8,
∴P点坐标为(﹣8,0).
21世纪教育网(www.21cnjy.com)
同课章节目录
