2025年九年级中考数学三轮冲刺练习反比例函数中的面积问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习反比例函数中的面积问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 852.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 05:14:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习反比例函数中的面积问题
1.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2(m≠0)的图象相交于A(1,3),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出y1>y2时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求△ABC的面积.
2.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于点A(﹣3,a),B(1,3),且一次函数与x轴,y轴分别交于点C,D.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式mx+n的解集;
(3)在第三象限的反比例函数图象上有一点P,使得S△OCP=4S△OBD,求点P的坐标.
3.如图,直线yx+b与反比例函数y的图象相交于点A,B,已知点A的纵坐标为6.
(1)求b的值;
(2)若点C是x轴上一点,且△ABC的面积为3,求点C的坐标.
4.如图,点A(a,2)在反比例函数y的图象上,AB∥x轴,且交y轴于点C,交反比例函数y于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y的解析式;
(3)点D为反比例函数y上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
5.如图所示,直线y=k1x+b与双曲线y交于A、B两点,已知点B的纵坐标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA,tan∠AOC.
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的2倍,求点P的坐标;
(3)直接写出不等式k1x+b的解集.
6.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
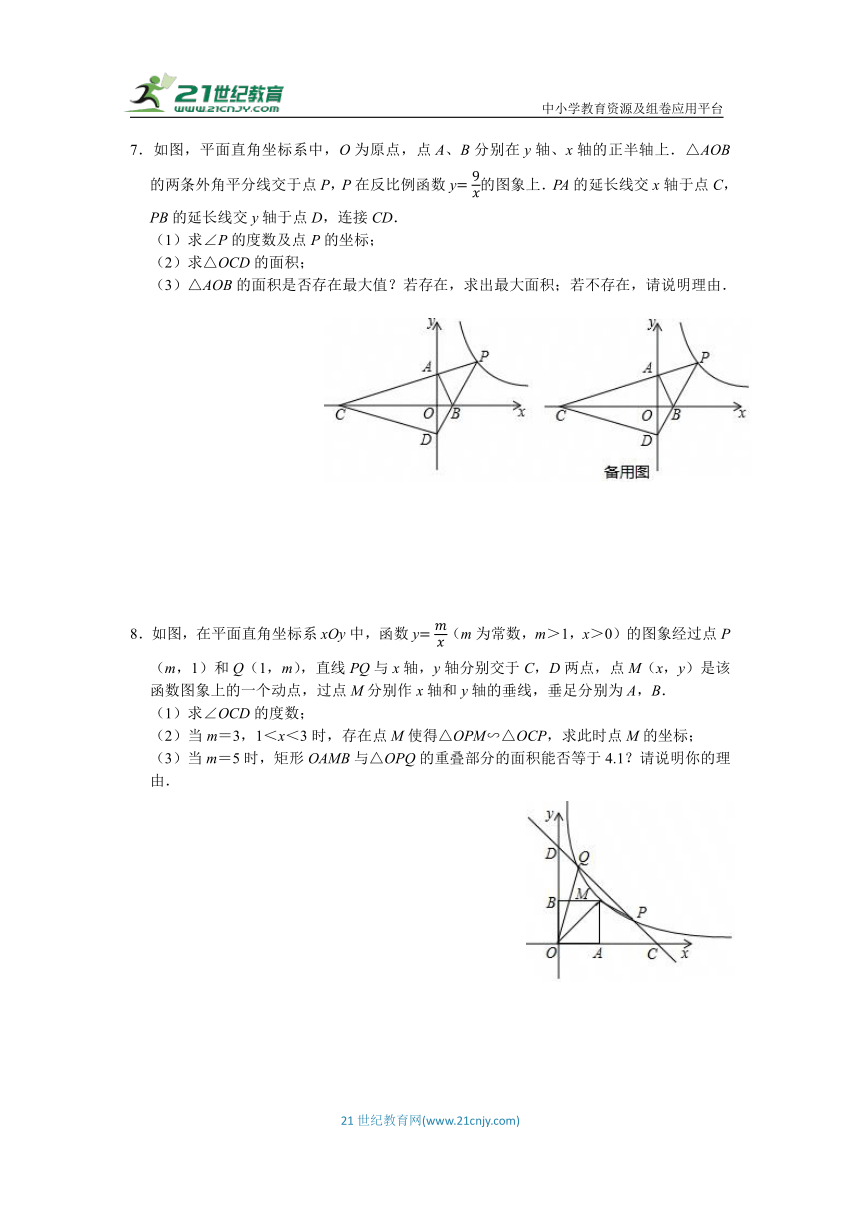
7.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
8.如图,在平面直角坐标系xOy中,函数y(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
9.平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
10.已知:一次函数y=﹣2x+10的图象与反比例函数y(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若,求△ABC的面积.
11.如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值;
(2)求△BMN面积的最大值;
(3)若MA⊥AB,求t的值.
12.如图,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交点A,B位于第二象限.已知A(﹣4,1),点B的纵坐标为4.
(1)求反比例函数和一次函数的表达式式;
(2)依据图象,直接写出不等式的解集;
(3)设点P是y轴上任意一点,若△PAB的面积等于3,求点P的坐标.
13.如图,一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,﹣3)两点,与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出不等式的解集.
(3)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,当△CDE的面积最大时,求点E的坐标,并求出面积的最大值.
14.如图,一次函数的图象与反比例函数的图象交于A(a,1),B(﹣2,b)两点,与x轴相交于点C.
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式的解集;
(3)若P(m,0)为x轴上的一动点,连接AP,当△APC的面积为时,求点P的坐标.
15.如图,已知反比例函数与正方形ABCO交于点M,N(1,),连接ON,以点O为圆心,ON长为半径作四分之一圆,分别交x轴,y轴正半轴于点D,E.
(1)求反比例函数的解析式;
(2)求证:BM=BN;
(3)如图所示,阴影部分面积和:S1+S2+S3= .
参考答案
1.【解答】解:(1)将点A坐标代入反比例函数解析式得,
m=1×3=3,
所以反比例函数解析式为y.
将点B坐标代入反比例函数解析式得,
n=﹣3,
所以点B的坐标为(﹣3,﹣1).
将A,B两点坐标代入一次函数解析式得,
,
解得,
所以一次函数解析式为y=x+2.
(2)由函数图象可知,
当﹣3<x<0或x>1时,一次函数的图象在反比例函数图象的上方,即y1>y2,
所以当y1>y2,x的取值范围是:﹣3<x<0或x>1.
(3)连接AO,令直线AB与x轴的交点为M,
将y=0代入y=x+2得,
x=﹣2,
所以点M的坐标为(﹣2,0),
所以S△AOB=S△AOM+S△BOM.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以BO=CO,
所以S△ABC=2S△AOB=8.
2.【解答】解:(1)∵一次函数y=mx+n(m≠0)的图象与反比例函数y的图象交于点A(﹣3,a),B(1,3),
∴k=1×3=﹣3×a,
∴k=3,a=﹣1,
∴反比例函数解析式为y,
一次函数y=mx+n图象过A(﹣3,﹣1),B(1,3),
,解得,
一次函数解析式为y=x+2;
(2)由图象可知,不等式mx+n的解集为:﹣3<x<0或x>1.
(3)在一次函数y=x+2中,当x=0时,y=2;当y=0时,x=﹣2,
∴C(﹣2,0),D(0,2)
∴S△OBD1,
∴S△OCP=4S△OBD=4,
设点P的坐标为(m,),
∴4,
解得m,
∴点P(,﹣4).
3.【解答】解:(1)∵点A在反比例函数y上,且A的纵坐标为6,
∴点A(2,6),
∵直线yx+b经过点A,
∴62+b,
∴b=9;
(2)如图,设直线AB与x轴的交点为D,
设点C(a,0),
∵直线AB与x轴的交点为D,
∴点D(6,0),
由题意可得:,
∴,,
∴点B(4,3),
∵S△ACB=S△ACD﹣S△BCD,
∴3CD×(6﹣3),
∴CD=2,
∴点C(4,0)或(8,0).
4.【解答】解:(1)∵点A(a,2)在反比例函数y的图象上,
∴2,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y得:2,
∴k=﹣2,
∴反比例函数y的解析式为y;
(3)设D(t,),而A(2,2),
∴AD中点E(,1),
而E在y轴上,
∴0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOEOE |xD|2,
S△AOEOE |xA|2,
∴△OAD面积S=S△DOE+S△AOE=3.
5.【解答】解:(1)如图1,
过点A作AE⊥x轴于E,
∴∠AEO=90°,
在Rt△AOE中,tan∠AOC,
设AE=m,则OE=2m,
根据勾股定理得,AE2+OE2=OA2,
∴m2+(2m)2=()2,
∴m=1或m=﹣1(舍),
∴OE=2,AE=1,
∴A(﹣2,1),
∵点A在双曲线y上,
∴k2=﹣2×1=﹣2,
∴双曲线的解析式为y,
∵点B在双曲线上,且纵坐标为﹣3,
∴﹣3,
∴x,
∴B(,﹣3),
将点A(﹣2,1),B(,﹣3)代入直线y=k1x+b中得,,
∴,
∴直线AB的解析式为yx﹣2;
(2)如图2,连接OB,PO,PC;
∵D(0,﹣2),
∴OD=2,
由(1)知,B(,﹣3),
∴S△ODBOD xB2,
∵△OCP的面积是△ODB的面积的2倍,
∴S△OCP=2S△ODB=2,
由(1)知,直线AB的解析式为yx﹣2,
令y=0,则x﹣2=0,
∴x,
∴OC,
设点P的纵坐标为n,
∴S△OCPOC yPn,
∴n=2,
由(1)知,双曲线的解析式为y,
∵点P在双曲线上,
∴2,
∴x=﹣1,
∴P(﹣1,2);
(3)由(1)知,A(﹣2,1),B(,﹣3),
由图象知,不等式k1x+b的解集为﹣2≤x<0或x.
6.【解答】(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,
∵AE⊥y轴,
∴AE∥OF,
∴四边形AEFO是平行四边形;
②解:过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,
∴AE∥BD,
∴△AEO∽△BDO,
∴,
∴当k=4时,,
即,
∴S△BOE=2S△AOE=1;
(2)不改变.
理由如下:
过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),
则AE=a,OE,PH,
∵四边形AEGO是平行四边形,
∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,
∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,
∴△AEO∽△GHP,
∴,
∵GH=OH﹣OG=﹣b﹣a,
∴,
∴k=0,
解得,
∵a,b异号,k>0,
∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
7.【解答】解:(1)如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在y上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=6a+6b﹣18,
∴3a+3b﹣9ab,
∵PM∥OC,
∴,
∴,
∴OC,同法可得OD,
∴S△COD OC DO 9.
解法二:连接OP.
∵∠POA=∠POB=∠CPD=45°,
∴∠COP=∠POD=135°,
∵∠POB=∠PCO+∠OPC=45°,∠APO+∠OPD=45°,
∴∠PCO=∠OPD,
∴△COP∽△POD,
∴OC OD=OP2=18,可求△COD的面积等于9.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴a+b6,
∴26,
∴(2)6,
∴3(2),
∴ab≤54﹣36,
∴S△AOBab≤27﹣18,
∴△AOB的面积的最大值为27﹣18.
8.【解答】解:(1)设直线PQ的解析式为y=kx+b,则有,
解得,
∴y=﹣x+m+1,
令x=0,得到y=m+1,∴D(0,m+1),
令y=0,得到x=m+1,∴C(m+1,0),
∴OC=OD,
∵∠COD=90°,
∴∠OCD=45°.
(2)设M(a,),
∵△OPM∽△OCP,
∴,
∴OP2=OC OM,
当m=3时,P(3,1),C(4,0),
OP2=32+12=10,OC=4,OM,
∴,
∴10=4,
∴4a4﹣25a2+36=0,
(4a2﹣9)(a2﹣4)=0,
∴a=±,a=±2,
∵1<a<3,
∴a或2,
当a时,M(,2),
PM,CP,
(舍弃),
当a=2时,M(2,),PM,CP,
∴,成立,
∴M(2,).
解法二:∵△OPM∽△OCP,
∴()2,
∵S△OCP=2,
∴S△OPM,
∴3×(),
解得,x=2或(舍弃),
∴M(2,).
(3)不存在.理由如下:
当m=5时,P(5,1),Q(1,5),设M(x,),
OP的解析式为:yx,OQ的解析式为y=5x,
①当1<x<5时,如图1中,
∴E(,),F(x,x),
S=S矩形OAMB﹣S△OAF﹣S△OBE
=5 x x 4.1,
化简得到:x4﹣9x2+25=0,
Δ<0,
∴没有实数根.
②当x≤1时,如图2中,
S=S△OGH<S△OAM=2.5,
∴不存在,
③当x≥5时,如图3中,
S=S△OTS<S△OBM=2.5,
∴不存在,
综上所述,不存在.
9.【解答】解:(1)①由已知,点B(4,2)在y1(x>0)的图象上
∴k=8
∴y1
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n
解得
∴y2=x﹣2
②当y1>y2>0时,y1图象在y2=x﹣2图象上方,且两函数图象在x轴上方
∴由图象得:2<x<4
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO
∵O为AA′中点
S△AOBS△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,)(3a,)
∴
解得k=6
(3)由已知A(a,),则A′为(﹣a,)
把A′代入到y
∴n
∴A′D解析式为y
当x=a时,点D纵坐标为
∴AD
∵AD=AF,
∴点F和点P横坐标为
∴点P纵坐标为
∴点P在y1(x>0)的图象上
10.【解答】解:(1)把A(4,2)代入y,得k=4×2=8.
∴反比例函数的解析式为y.
解方程组,得
或,
∴点B的坐标为(1,8);
(2)①若∠BAP=90°,
过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,
对于y=﹣2x+10,
当y=0时,﹣2x+10=0,解得x=5,
∴点E(5,0),OE=5.
∵A(4,2),∴OH=4,AH=2,
∴HE=5﹣4=1.
∵AH⊥OE,∴∠AHM=∠AHE=90°.
又∵∠BAP=90°,
∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,
∴∠MAH=∠AEM,
∴△AHM∽△EHA,
∴,
∴,
∴MH=4,
∴M(0,0),
可设直线AP的解析式为y=mx
则有4m=2,解得m,
∴直线AP的解析式为yx,
解方程组,得
或,
∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,
同理可得:点P的坐标为(﹣16,).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,
则有BS∥CT,
∴△CTD∽△BSD,
∴.
∵,
∴.
∵A(a,﹣2a+10),B(b,﹣2b+10),
∴C(﹣a,2a﹣10),CT=a,BS=b,
∴,即ba.
∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数y的图象上,
∴a(﹣2a+10)=b(﹣2b+10),
∴a(﹣2a+10)a(﹣2a+10).
∵a≠0,
∴﹣2a+10(﹣2a+10),
解得:a=3.
∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为y=px+q,
则有,
解得:,
∴直线BC的解析式为y=2x+2.
当x=0时,y=2,则点D(0,2),OD=2,
∴S△COB=S△ODC+S△ODB
OD CTOD BS
2×32×2=5.
∵OA=OC,
∴S△AOB=S△COB,
∴S△ABC=2S△COB=10.
11.【解答】解:(1)把点A(8,1)代入反比例函数y(x>0)得:
k=1×8=8,y,
∴k=8;
(2)设直线AB的解析式为:y=kx+b,
根据题意得:,
解得:k,b=﹣3,
∴直线AB的解析式为:yx﹣3;
设M(t,),N(t,t﹣3),
则MNt+3,
∴△BMN的面积S(t+3)tt2t+4(t﹣3)2,
∴△BMN的面积S是t的二次函数,
∵0,
∴S有最大值,
当t=3时,△BMN的面积的最大值为;
(3)∵MA⊥AB,
∴设直线MA的解析式为:y=﹣2x+c,
把点A(8,1)代入得:c=17,
∴直线AM的解析式为:y=﹣2x+17,
解方程组 得: 或 (舍去),
∴M的坐标为(,16),
∴t.
12.【解答】解:(1)将点A的坐标代入反比例函数表达式得:m=﹣4×1=﹣4,
则反比例函数的表达式为:y,
当y=4时,x=﹣1,即点B(﹣1,4),
则y=k(x+1)+4,
将点A的坐标代入上式得:1=k(﹣4+1)+4,则k=1,
即一次函数的表达式为:y=x+5;
(2)观察函数图象知,不等式的解集为﹣4<x<﹣1;
(3)当点P在AB下方时,
过点P作直线PH∥AB交x轴于点H,过点C作CN⊥PH于点N,
由点A、B的坐标得,AB=3,
则△PAB的面积AB×CNCN=3,
则CN,
由直线AB的表达式知,∠BCO=45°,则∠HCN=45°,
则CHCN=2,
则直线PH的表达式为:y=(x﹣2)+5=x+3,
则点P(0,3);
当点P在AB上方时,
同理可得,过点P和AB平行的直线的表达式为y=x+7,
则点P(0,7),
综上,P(0,3)或(0,7).
13.【解答】解:(1)∵B(2,﹣3)点在反比例函数图象上,
∴k=﹣6;
∴反比例函数解析式为y,
∵A(m,1)点在反比例函数图象上,
∴1,解得x=﹣6,
∴A(﹣6,1),B(2,﹣3),
∵A(﹣6,1),B(2,﹣3)在一次函数y=ax+b的图象上,
则,解得:,
∴一次函数解析式为:yx﹣2;
(2)观察函数图象知,不等式的解集为:x<﹣6或0<x<2;
(3)由(1)可知C(0,﹣2),设点D的坐标为(m,m﹣2),则E(m,),
∴ED(m﹣2)m+2,
∴S△CDE(﹣m)×(m+2)(m+2)2+4,
当m=﹣2时,S△CDE最大值为4,
∴E(﹣2,3).
14.【解答】解:(1)∵函数的图象经过A(a,1),
∴,
解得:a=4,
∴A(4,1),
∴k=1×4=4,
∴反比例函数表达式为:;
(2)∵函数的图象经过B(﹣2,b),
∴,
∴B(﹣2,﹣2),
∴由图可得,不等式的解集是:x<﹣2或0<x<4;
(3)如图:
在中,当y=0时,得,
解得:x=2,
∴C(2,0),
∵P(0,m),
∴PC=|m﹣2|,
∵S△APC,A(4,1),
∴,
解得:m=﹣3或7,
∴点P的坐标为(﹣3,0)或(7,0).
15.【解答】解:(1)∵反比例函数 与正方形ABCO交于点M,,
∴将 代入 中,得:,
解得,
∴反比例函数的解析式为;
(2)∵,四边形ABCO是正方形,
∴OA=BC=AB=OC,
∴点M的横坐标为,
把代入中得,y=1,
∴,
∴AM=1,
∴,
∵,
∴CN=1,
∴,
∴BM=BN;
(3)连接OM,
在Rt△OCN中,∵N(1,),
∴OC,CN=1,
∴tan∠CON,
∴∠CON=30°,
同理,∠AOM=30°,
∴∠MON=60°,
∵ON2,
∴S1+S2=S扇形DOE﹣S△CON﹣S△AOM11π,
S3=S正方形ABCO﹣S扇形NOM﹣S△CON﹣S△AOM
113,
∴S1+S2+S3=π33π﹣2,
故答案为:3π﹣2.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习反比例函数中的面积问题
1.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2(m≠0)的图象相交于A(1,3),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出y1>y2时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求△ABC的面积.
2.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于点A(﹣3,a),B(1,3),且一次函数与x轴,y轴分别交于点C,D.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式mx+n的解集;
(3)在第三象限的反比例函数图象上有一点P,使得S△OCP=4S△OBD,求点P的坐标.
3.如图,直线yx+b与反比例函数y的图象相交于点A,B,已知点A的纵坐标为6.
(1)求b的值;
(2)若点C是x轴上一点,且△ABC的面积为3,求点C的坐标.
4.如图,点A(a,2)在反比例函数y的图象上,AB∥x轴,且交y轴于点C,交反比例函数y于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y的解析式;
(3)点D为反比例函数y上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
5.如图所示,直线y=k1x+b与双曲线y交于A、B两点,已知点B的纵坐标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA,tan∠AOC.
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的2倍,求点P的坐标;
(3)直接写出不等式k1x+b的解集.
6.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
7.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
8.如图,在平面直角坐标系xOy中,函数y(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
9.平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
10.已知:一次函数y=﹣2x+10的图象与反比例函数y(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若,求△ABC的面积.
11.如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值;
(2)求△BMN面积的最大值;
(3)若MA⊥AB,求t的值.
12.如图,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交点A,B位于第二象限.已知A(﹣4,1),点B的纵坐标为4.
(1)求反比例函数和一次函数的表达式式;
(2)依据图象,直接写出不等式的解集;
(3)设点P是y轴上任意一点,若△PAB的面积等于3,求点P的坐标.
13.如图,一次函数y=ax+b的图象与反比例函数的图象相交于A(m,1),B(2,﹣3)两点,与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出不等式的解集.
(3)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,当△CDE的面积最大时,求点E的坐标,并求出面积的最大值.
14.如图,一次函数的图象与反比例函数的图象交于A(a,1),B(﹣2,b)两点,与x轴相交于点C.
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式的解集;
(3)若P(m,0)为x轴上的一动点,连接AP,当△APC的面积为时,求点P的坐标.
15.如图,已知反比例函数与正方形ABCO交于点M,N(1,),连接ON,以点O为圆心,ON长为半径作四分之一圆,分别交x轴,y轴正半轴于点D,E.
(1)求反比例函数的解析式;
(2)求证:BM=BN;
(3)如图所示,阴影部分面积和:S1+S2+S3= .
参考答案
1.【解答】解:(1)将点A坐标代入反比例函数解析式得,
m=1×3=3,
所以反比例函数解析式为y.
将点B坐标代入反比例函数解析式得,
n=﹣3,
所以点B的坐标为(﹣3,﹣1).
将A,B两点坐标代入一次函数解析式得,
,
解得,
所以一次函数解析式为y=x+2.
(2)由函数图象可知,
当﹣3<x<0或x>1时,一次函数的图象在反比例函数图象的上方,即y1>y2,
所以当y1>y2,x的取值范围是:﹣3<x<0或x>1.
(3)连接AO,令直线AB与x轴的交点为M,
将y=0代入y=x+2得,
x=﹣2,
所以点M的坐标为(﹣2,0),
所以S△AOB=S△AOM+S△BOM.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以BO=CO,
所以S△ABC=2S△AOB=8.
2.【解答】解:(1)∵一次函数y=mx+n(m≠0)的图象与反比例函数y的图象交于点A(﹣3,a),B(1,3),
∴k=1×3=﹣3×a,
∴k=3,a=﹣1,
∴反比例函数解析式为y,
一次函数y=mx+n图象过A(﹣3,﹣1),B(1,3),
,解得,
一次函数解析式为y=x+2;
(2)由图象可知,不等式mx+n的解集为:﹣3<x<0或x>1.
(3)在一次函数y=x+2中,当x=0时,y=2;当y=0时,x=﹣2,
∴C(﹣2,0),D(0,2)
∴S△OBD1,
∴S△OCP=4S△OBD=4,
设点P的坐标为(m,),
∴4,
解得m,
∴点P(,﹣4).
3.【解答】解:(1)∵点A在反比例函数y上,且A的纵坐标为6,
∴点A(2,6),
∵直线yx+b经过点A,
∴62+b,
∴b=9;
(2)如图,设直线AB与x轴的交点为D,
设点C(a,0),
∵直线AB与x轴的交点为D,
∴点D(6,0),
由题意可得:,
∴,,
∴点B(4,3),
∵S△ACB=S△ACD﹣S△BCD,
∴3CD×(6﹣3),
∴CD=2,
∴点C(4,0)或(8,0).
4.【解答】解:(1)∵点A(a,2)在反比例函数y的图象上,
∴2,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y得:2,
∴k=﹣2,
∴反比例函数y的解析式为y;
(3)设D(t,),而A(2,2),
∴AD中点E(,1),
而E在y轴上,
∴0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOEOE |xD|2,
S△AOEOE |xA|2,
∴△OAD面积S=S△DOE+S△AOE=3.
5.【解答】解:(1)如图1,
过点A作AE⊥x轴于E,
∴∠AEO=90°,
在Rt△AOE中,tan∠AOC,
设AE=m,则OE=2m,
根据勾股定理得,AE2+OE2=OA2,
∴m2+(2m)2=()2,
∴m=1或m=﹣1(舍),
∴OE=2,AE=1,
∴A(﹣2,1),
∵点A在双曲线y上,
∴k2=﹣2×1=﹣2,
∴双曲线的解析式为y,
∵点B在双曲线上,且纵坐标为﹣3,
∴﹣3,
∴x,
∴B(,﹣3),
将点A(﹣2,1),B(,﹣3)代入直线y=k1x+b中得,,
∴,
∴直线AB的解析式为yx﹣2;
(2)如图2,连接OB,PO,PC;
∵D(0,﹣2),
∴OD=2,
由(1)知,B(,﹣3),
∴S△ODBOD xB2,
∵△OCP的面积是△ODB的面积的2倍,
∴S△OCP=2S△ODB=2,
由(1)知,直线AB的解析式为yx﹣2,
令y=0,则x﹣2=0,
∴x,
∴OC,
设点P的纵坐标为n,
∴S△OCPOC yPn,
∴n=2,
由(1)知,双曲线的解析式为y,
∵点P在双曲线上,
∴2,
∴x=﹣1,
∴P(﹣1,2);
(3)由(1)知,A(﹣2,1),B(,﹣3),
由图象知,不等式k1x+b的解集为﹣2≤x<0或x.
6.【解答】(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,
∵AE⊥y轴,
∴AE∥OF,
∴四边形AEFO是平行四边形;
②解:过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,
∴AE∥BD,
∴△AEO∽△BDO,
∴,
∴当k=4时,,
即,
∴S△BOE=2S△AOE=1;
(2)不改变.
理由如下:
过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),
则AE=a,OE,PH,
∵四边形AEGO是平行四边形,
∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,
∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,
∴△AEO∽△GHP,
∴,
∵GH=OH﹣OG=﹣b﹣a,
∴,
∴k=0,
解得,
∵a,b异号,k>0,
∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
7.【解答】解:(1)如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在y上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=6a+6b﹣18,
∴3a+3b﹣9ab,
∵PM∥OC,
∴,
∴,
∴OC,同法可得OD,
∴S△COD OC DO 9.
解法二:连接OP.
∵∠POA=∠POB=∠CPD=45°,
∴∠COP=∠POD=135°,
∵∠POB=∠PCO+∠OPC=45°,∠APO+∠OPD=45°,
∴∠PCO=∠OPD,
∴△COP∽△POD,
∴OC OD=OP2=18,可求△COD的面积等于9.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴a+b6,
∴26,
∴(2)6,
∴3(2),
∴ab≤54﹣36,
∴S△AOBab≤27﹣18,
∴△AOB的面积的最大值为27﹣18.
8.【解答】解:(1)设直线PQ的解析式为y=kx+b,则有,
解得,
∴y=﹣x+m+1,
令x=0,得到y=m+1,∴D(0,m+1),
令y=0,得到x=m+1,∴C(m+1,0),
∴OC=OD,
∵∠COD=90°,
∴∠OCD=45°.
(2)设M(a,),
∵△OPM∽△OCP,
∴,
∴OP2=OC OM,
当m=3时,P(3,1),C(4,0),
OP2=32+12=10,OC=4,OM,
∴,
∴10=4,
∴4a4﹣25a2+36=0,
(4a2﹣9)(a2﹣4)=0,
∴a=±,a=±2,
∵1<a<3,
∴a或2,
当a时,M(,2),
PM,CP,
(舍弃),
当a=2时,M(2,),PM,CP,
∴,成立,
∴M(2,).
解法二:∵△OPM∽△OCP,
∴()2,
∵S△OCP=2,
∴S△OPM,
∴3×(),
解得,x=2或(舍弃),
∴M(2,).
(3)不存在.理由如下:
当m=5时,P(5,1),Q(1,5),设M(x,),
OP的解析式为:yx,OQ的解析式为y=5x,
①当1<x<5时,如图1中,
∴E(,),F(x,x),
S=S矩形OAMB﹣S△OAF﹣S△OBE
=5 x x 4.1,
化简得到:x4﹣9x2+25=0,
Δ<0,
∴没有实数根.
②当x≤1时,如图2中,
S=S△OGH<S△OAM=2.5,
∴不存在,
③当x≥5时,如图3中,
S=S△OTS<S△OBM=2.5,
∴不存在,
综上所述,不存在.
9.【解答】解:(1)①由已知,点B(4,2)在y1(x>0)的图象上
∴k=8
∴y1
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n
解得
∴y2=x﹣2
②当y1>y2>0时,y1图象在y2=x﹣2图象上方,且两函数图象在x轴上方
∴由图象得:2<x<4
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO
∵O为AA′中点
S△AOBS△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,)(3a,)
∴
解得k=6
(3)由已知A(a,),则A′为(﹣a,)
把A′代入到y
∴n
∴A′D解析式为y
当x=a时,点D纵坐标为
∴AD
∵AD=AF,
∴点F和点P横坐标为
∴点P纵坐标为
∴点P在y1(x>0)的图象上
10.【解答】解:(1)把A(4,2)代入y,得k=4×2=8.
∴反比例函数的解析式为y.
解方程组,得
或,
∴点B的坐标为(1,8);
(2)①若∠BAP=90°,
过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,
对于y=﹣2x+10,
当y=0时,﹣2x+10=0,解得x=5,
∴点E(5,0),OE=5.
∵A(4,2),∴OH=4,AH=2,
∴HE=5﹣4=1.
∵AH⊥OE,∴∠AHM=∠AHE=90°.
又∵∠BAP=90°,
∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,
∴∠MAH=∠AEM,
∴△AHM∽△EHA,
∴,
∴,
∴MH=4,
∴M(0,0),
可设直线AP的解析式为y=mx
则有4m=2,解得m,
∴直线AP的解析式为yx,
解方程组,得
或,
∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,
同理可得:点P的坐标为(﹣16,).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,
则有BS∥CT,
∴△CTD∽△BSD,
∴.
∵,
∴.
∵A(a,﹣2a+10),B(b,﹣2b+10),
∴C(﹣a,2a﹣10),CT=a,BS=b,
∴,即ba.
∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数y的图象上,
∴a(﹣2a+10)=b(﹣2b+10),
∴a(﹣2a+10)a(﹣2a+10).
∵a≠0,
∴﹣2a+10(﹣2a+10),
解得:a=3.
∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为y=px+q,
则有,
解得:,
∴直线BC的解析式为y=2x+2.
当x=0时,y=2,则点D(0,2),OD=2,
∴S△COB=S△ODC+S△ODB
OD CTOD BS
2×32×2=5.
∵OA=OC,
∴S△AOB=S△COB,
∴S△ABC=2S△COB=10.
11.【解答】解:(1)把点A(8,1)代入反比例函数y(x>0)得:
k=1×8=8,y,
∴k=8;
(2)设直线AB的解析式为:y=kx+b,
根据题意得:,
解得:k,b=﹣3,
∴直线AB的解析式为:yx﹣3;
设M(t,),N(t,t﹣3),
则MNt+3,
∴△BMN的面积S(t+3)tt2t+4(t﹣3)2,
∴△BMN的面积S是t的二次函数,
∵0,
∴S有最大值,
当t=3时,△BMN的面积的最大值为;
(3)∵MA⊥AB,
∴设直线MA的解析式为:y=﹣2x+c,
把点A(8,1)代入得:c=17,
∴直线AM的解析式为:y=﹣2x+17,
解方程组 得: 或 (舍去),
∴M的坐标为(,16),
∴t.
12.【解答】解:(1)将点A的坐标代入反比例函数表达式得:m=﹣4×1=﹣4,
则反比例函数的表达式为:y,
当y=4时,x=﹣1,即点B(﹣1,4),
则y=k(x+1)+4,
将点A的坐标代入上式得:1=k(﹣4+1)+4,则k=1,
即一次函数的表达式为:y=x+5;
(2)观察函数图象知,不等式的解集为﹣4<x<﹣1;
(3)当点P在AB下方时,
过点P作直线PH∥AB交x轴于点H,过点C作CN⊥PH于点N,
由点A、B的坐标得,AB=3,
则△PAB的面积AB×CNCN=3,
则CN,
由直线AB的表达式知,∠BCO=45°,则∠HCN=45°,
则CHCN=2,
则直线PH的表达式为:y=(x﹣2)+5=x+3,
则点P(0,3);
当点P在AB上方时,
同理可得,过点P和AB平行的直线的表达式为y=x+7,
则点P(0,7),
综上,P(0,3)或(0,7).
13.【解答】解:(1)∵B(2,﹣3)点在反比例函数图象上,
∴k=﹣6;
∴反比例函数解析式为y,
∵A(m,1)点在反比例函数图象上,
∴1,解得x=﹣6,
∴A(﹣6,1),B(2,﹣3),
∵A(﹣6,1),B(2,﹣3)在一次函数y=ax+b的图象上,
则,解得:,
∴一次函数解析式为:yx﹣2;
(2)观察函数图象知,不等式的解集为:x<﹣6或0<x<2;
(3)由(1)可知C(0,﹣2),设点D的坐标为(m,m﹣2),则E(m,),
∴ED(m﹣2)m+2,
∴S△CDE(﹣m)×(m+2)(m+2)2+4,
当m=﹣2时,S△CDE最大值为4,
∴E(﹣2,3).
14.【解答】解:(1)∵函数的图象经过A(a,1),
∴,
解得:a=4,
∴A(4,1),
∴k=1×4=4,
∴反比例函数表达式为:;
(2)∵函数的图象经过B(﹣2,b),
∴,
∴B(﹣2,﹣2),
∴由图可得,不等式的解集是:x<﹣2或0<x<4;
(3)如图:
在中,当y=0时,得,
解得:x=2,
∴C(2,0),
∵P(0,m),
∴PC=|m﹣2|,
∵S△APC,A(4,1),
∴,
解得:m=﹣3或7,
∴点P的坐标为(﹣3,0)或(7,0).
15.【解答】解:(1)∵反比例函数 与正方形ABCO交于点M,,
∴将 代入 中,得:,
解得,
∴反比例函数的解析式为;
(2)∵,四边形ABCO是正方形,
∴OA=BC=AB=OC,
∴点M的横坐标为,
把代入中得,y=1,
∴,
∴AM=1,
∴,
∵,
∴CN=1,
∴,
∴BM=BN;
(3)连接OM,
在Rt△OCN中,∵N(1,),
∴OC,CN=1,
∴tan∠CON,
∴∠CON=30°,
同理,∠AOM=30°,
∴∠MON=60°,
∵ON2,
∴S1+S2=S扇形DOE﹣S△CON﹣S△AOM11π,
S3=S正方形ABCO﹣S扇形NOM﹣S△CON﹣S△AOM
113,
∴S1+S2+S3=π33π﹣2,
故答案为:3π﹣2.
21世纪教育网(www.21cnjy.com)
同课章节目录
