3.9弧长及扇形的面积同步练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 3.9弧长及扇形的面积同步练习 北师大版数学九年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 985.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
2.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是
A.4π B.8π C.12π D.16π
3.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
4.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
5.用一个圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的高为( )
A. B. C. D.
6.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B.1 C. D.4
7.“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
8.一个扇形的半径为60cm,圆心角为120°,用它做一个圆锥的侧面,则圆锥的底面半径为
A.5cm B.10cm C.20cm D.30cm
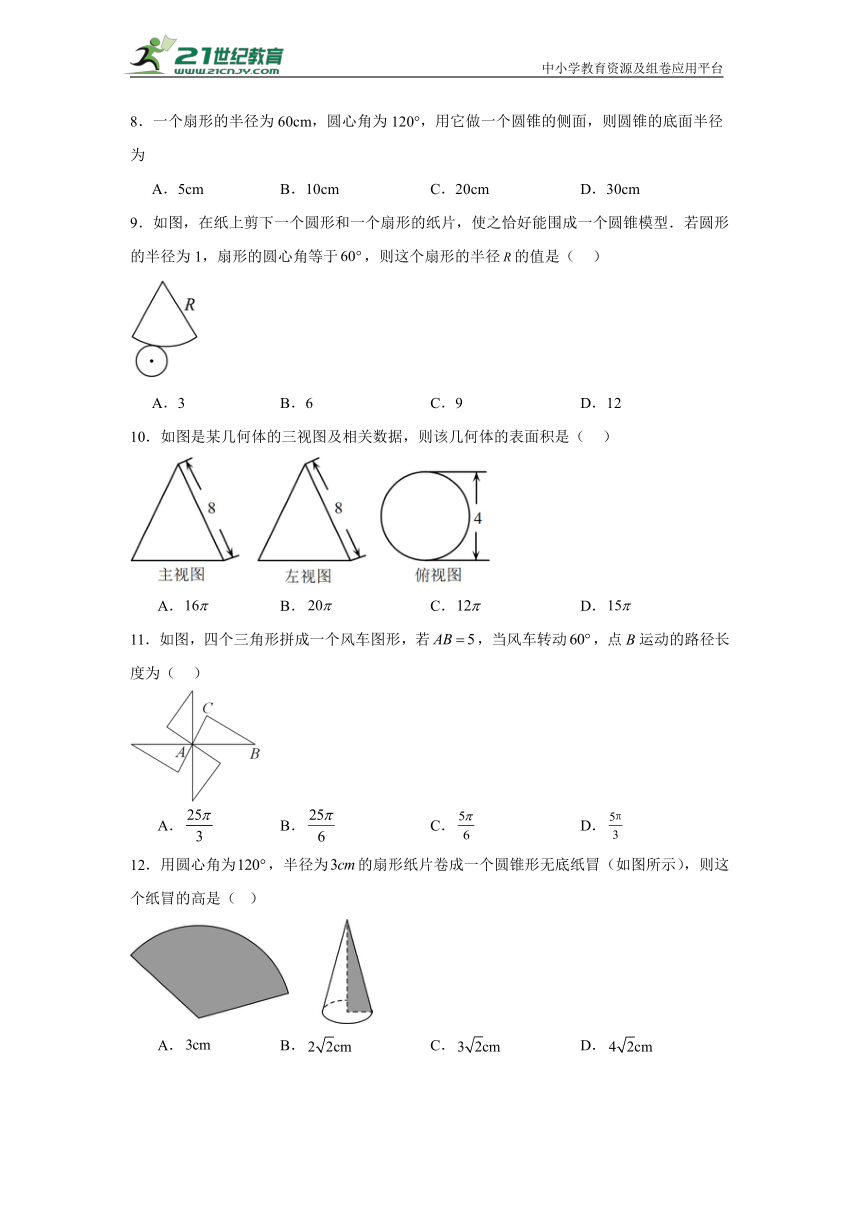
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆形的半径为1,扇形的圆心角等于,则这个扇形的半径的值是( )
A.3 B.6 C.9 D.12
10.如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
A. B. C. D.
11.如图,四个三角形拼成一个风车图形,若,当风车转动,点B运动的路径长度为( )
A. B. C. D.
12.用圆心角为,半径为的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
A. B. C. D.
二、填空题
13.一个圆锥形零件经过轴的剖面是一个等边三角形,若它的高为5cm,则它的全面积等于 ;
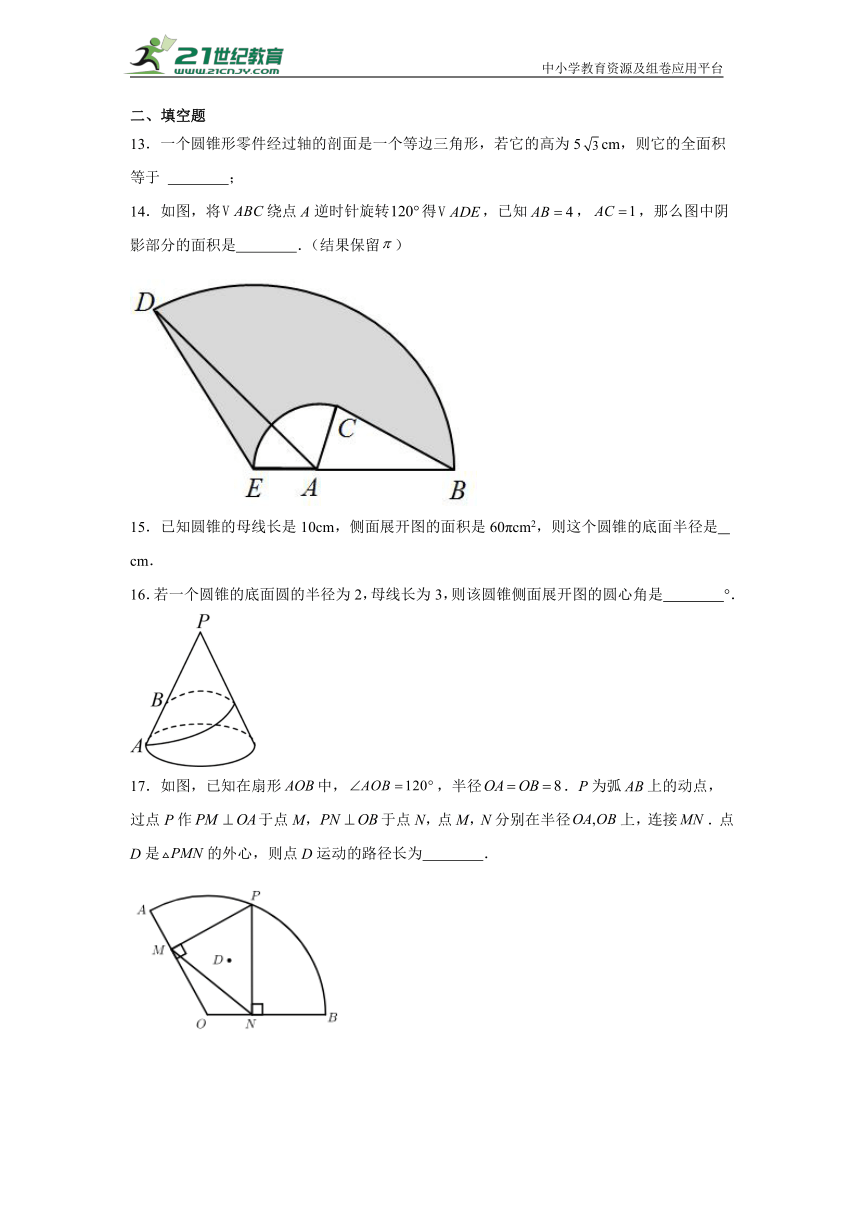
14.如图,将绕点A逆时针旋转得,已知,,那么图中阴影部分的面积是 .(结果保留)
15.已知圆锥的母线长是10cm,侧面展开图的面积是60πcm2,则这个圆锥的底面半径是 cm.
16.若一个圆锥的底面圆的半径为2,母线长为3,则该圆锥侧面展开图的圆心角是 °.
17.如图,已知在扇形中,,半径.P为弧上的动点,过点P作于点M,于点N,点M,N分别在半径上,连接.点D是的外心,则点D运动的路径长为 .
三、解答题
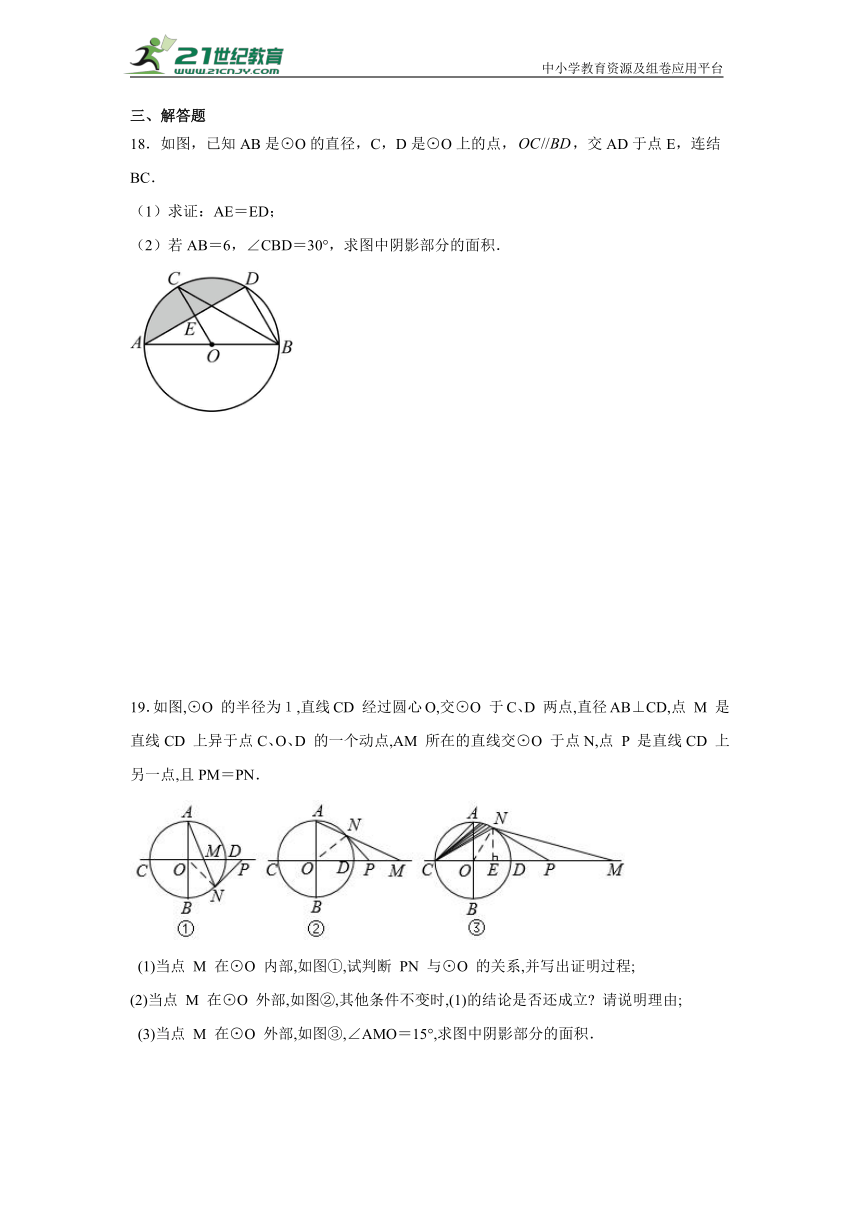
18.如图,已知AB是⊙O的直径,C,D是⊙O上的点,,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
19.如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.
(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
20.如图,半径为6的⊙O与Rt△ABC的边AB相切于点A,交边BC于点C,D,∠B=90°,连接OD,AD.
(1)若∠ACB=20°,求的长(结果保留).
(2)求证:AD平分∠BDO.
21.如图,在平面直角坐标系中,已知的三个顶点的坐标分别为.
(1)外接圆的圆心的坐标是______;
(2)求该圆圆心到弦的距离;
(3)以所在直线为旋转轴,将旋转一周,求所得几何体的表面积.
22.如图,粮仓的顶部是圆锥形,这个圆锥的底面周长为30cm,母线长为7cm,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是多少
23.在航海中,常用海里(单位:)作为路程的度量单位,把地球看作球体,近似等于赤道所在的圆中的圆心角所对的弧长,已知地球半径(也就是赤道所在圆的半径)约为约等于多少米(取3.14,结果取整数)?
24.上海外滩海关大钟时针长约为6米,从上午9时到当天下午6时,时针的针尖走过的路程是多少米?(取π=3.14)
《3.9弧长及扇形的面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B B C C B B
题号 11 12
答案 D B
1.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
【详解】连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
【点睛】本题考查动点的运动轨迹问题,根据定弦定角确定圆的所在位置,以及等腰三角形的性质、中位线的性质、弧长公式,熟练掌握这些性质是解题的关键.
2.C
【分析】利用圆锥的侧面展开图为一扇形,再根据扇形的半径等于圆锥的母线长和扇形的面积公式计算.
【详解】解:该扇形的面积.
故选C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长
3.B
【分析】先求出该扇形的半径,再求其面积即可;
【详解】解:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
【点睛】本题主要考查扇形面积的求解,掌握扇形面积的求解公式是解题的关键.
4.C
【分析】根据弧长公式:l=(弧长为l,圆心角度数为n,圆的半径为R),代入即可求出圆心角的度数.
【详解】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
【点睛】本题考查了弧长的计算,解答本题关键是熟练掌握弧长的计算公式,及公式字母表示的含义.
5.B
【分析】根据题意直接利用圆锥的性质求出圆锥的半径,进而利用勾股定理得出圆锥的高.
【详解】解:设此圆锥的底面半径为r,由题意得:,
解得r=2cm,
故这个圆锥的高为:.
故选:B.
【点睛】本题主要考查圆锥的计算,熟练掌握圆锥的性质并正确得出圆锥的半径是解题关键.
6.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.设这个圆锥的底面圆半径为,利用弧长公式得到,然后解关于的方程即可.
【详解】解:设这个圆锥的底面圆半径为,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故选:B
7.C
【详解】∵底面圆的直径为8cm,高为3cm,
∴母线长为5cm,
∴其表面积=π×4×5+42×π+8π×6=84πcm2,
故选C.
8.C
【详解】试题分析:因为扇形的半径为60cm,圆心角为120°,所以扇形的弧长为,而扇形的弧长即为圆锥的底面周长,所以圆锥的底面半径为(cm)
考点:扇形和圆锥的转换关系
点评:扇形的弧长公式为,圆锥底面半径为
9.B
【分析】根据扇形的弧长与圆的周长相等,列方程求解即可.
【详解】解:由题意可得:,解得,
故选:B
【点睛】本题考查扇形弧长公式,圆的周长,掌握扇形弧长公式,圆的周长公式,抓住扇形弧长与圆的周长相等构造等式是解题关键.
10.B
【分析】根据三视图得到此几何体为圆锥,几何体的表面积=侧面积+底面面积,然后根据圆锥的侧面展开图为一扇形,求侧面积扇形面积=,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,底面利用圆的面积求解即可.
【详解】解:该几何体的表面积.
故选:B.
【点睛】本题考查了圆锥表面积的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图的识别.
11.D
【分析】根据题意可知:B点的运动路径是以A点为圆心,长为半径,风车转动的圆弧,计算即可.
【详解】解:,风车转动,
,
故选:D.
【点睛】本题考查了弧长的计算,解题的关键是掌握弧长公式:.
12.B
【分析】本题主要考查了扇形面积的计算.先求出扇形的弧长,根据扇形的弧长=圆锥的底面周长,用扇形的弧长,可求圆锥的底面半径,利用勾股定理得出答案.
【详解】解:∵扇形的弧长,
∴圆锥的底面半径为,
∴这个圆锥形筒的高为.
故选:B.
13.75πcm2
【分析】全面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【详解】圆锥的轴的剖面是一个等边三角形,它的高为cm,
则等边三角形的边长为10 cm,则底面半径=5cm,底面周长=10πcm,
底面面积=25πcm2,侧面面积=50πcm2,
∴圆锥的全面积=25π+50π=75πcm2.
故答案为75πcm2.
【点睛】圆锥是由一个底面和一个侧面围成的图形,我们把圆锥底面圆周上任意一点与圆锥顶点的连线叫做圆锥的母线,连接顶点与底面圆心的线段叫做圆锥的高.沿着圆锥的母线,把圆锥的侧面展开,得到一个扇形,这个扇形的弧长等于圆锥底面圆的周长,而扇形的半径等于圆锥的母线长.
14.
【分析】根据旋转的性质可以得到阴影部分的面积=扇形DAB的面积-扇形EAC的面积,利用扇形的面积公式即可求解.
【详解】解:∵将绕点A逆时针旋转得,
∴S△ABC= S△ADE,
∴阴影部分的面积=扇形DAB的面积+S△ADE -扇形EAC的面积-S△ABC
=扇形DAB的面积-扇形EAC的面积
∴阴影部分的面积,
故答案为:.
【点睛】本题考查了旋转的性质以及扇形的面积公式,根据旋转的性质推出:阴影部分的面积=扇形DAB的面积-扇形EAC的面积是解题关键.
15.6
【分析】圆锥的侧面积公式:圆锥的侧面积=π×母线×底面半径.
【详解】解:设圆锥的底面半径为R,由题意得
π×10R=60π,
解得R=6
则这个圆锥的底面半径是6cm.
【点睛】本题是圆锥的侧面积公式的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.
16.240
【分析】本题考查了圆锥的计算:理解圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键.
【详解】圆锥侧面展开图的弧长是,
设圆心角的度数是,则,
解得,
故答案为:.
17..
【分析】根据点在弧上运动,其路径也是一段弧,由题意可得,点运动路径所对的圆心角是,连接,取的中点,连接,,根据在和中,点是斜边的中点,可证得点,,,四点均在同一个圆,即上,过点作,垂足为点,由垂径定理,,,可求得,再根据点和点重合,得到点运动路径所对的圆心角是,根据弧长公式可求解.
【详解】解:点在弧上运动,其路径也是一段弧,由题意可知,
当点与点重合时,,
当点与点重合时,,
点运动路径所对的圆心角是,
如图,连接,取的中点,连接,,
在和中,点是斜边的中点,
,
根据圆的定义可知,点,,,四点均在同一个圆,即上,
又,,
,,
过点作,垂足为点,
由垂径定理得,,
在中,,,则,
,
∵是的外接圆的圆心,
即:点和点重合,如图2
,
点是以点为圆心为半径,
点运动路径所对的圆心角是,
点运动路径所对的圆心角是,
点运动的路径长为.
故答案是:.
【点睛】本题考查了直径所对的圆周角是直角,弧长公式,三角形的外心的性质,理解题意熟悉公式是解题的关键.
18.(1)证明见解析;(2).
【分析】(1)先根据圆的性质可得,再根据三角形的中位线定理即可得证;
(2)如图(见解析),先根据垂径定理、圆周角定理可得,从而可得,再根据直角三角形的性质、三角形的面积公式可得,然后根据圆周角定理可得,最后根据图中阴影部分的面积等于扇形OAD面积减去面积即可得.
【详解】(1)∵AB是的直径,
∴,即点O是AB的中点,
∵,
∴是的中位线,
点E是AD的中点,
∴;
(2)如图,连接OD,
∵AB是的直径,,
,,
∵,
,即,
又是的半径,
,
,
,,
在中,,
OD是的斜边AB上的中线,
,
又,
,
则图中阴影部分的面积为.
【点睛】本题考查了圆周角定理、垂径定理、扇形的面积公式、三角形中位线定理等知识点,较难的是题(2),熟练掌握圆周角定理和扇形的面积公式是解题关键.
19.(1)详见解析;(2)成立,理由详见解析;(3)+-.
【分析】(1)PN 与⊙O 相切.要证明ON⊥ PN即可,连接ON,PM=PN,所以∠PNM=∠PMN,∠AMO=∠PMN,AB⊥CD,所以∠PMN+∠MAO=90°,又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°,所以PN 与⊙O 相切.
(2)成立,进行等量代换,∠MAO+∠OMA=90°,因∠OMA=∠PNM,∠MAO=∠ONA,所以∠PNM+∠ONA=90°,所以∠ONP=90°;
(3)阴影部分的面积可通过S △AOC+S扇形AOC-S△ AON求得.
【详解】 (1)PN 与⊙O 相切.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
又∵∠AMO=∠PMN,
∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°,
即PN 与⊙O 相切.
(2)成立.理由如下:连接ON,则∠ONA=∠OAN.
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,∠OMA+∠OAM=90°.
∴∠PNM+∠ONA=90°,
∴∠PNO=180°-90°=90°.
即PN 与⊙O 相切.
(3)连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,
∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
过点N 作NE⊥OD,垂足为点E.则OE=.
∴NE=.
∴S阴影=S△AOC+S扇形AON-S△CON=OC·OA+-CO·NE
=+-
∴图中阴影部分的面积为+-
20.(1)
(2)见解析
【分析】(1)连接,由,得,由弧长公式即得的长为;
(2)根据切于点,,可得,有,而,即可得,从而平分.
【详解】(1)解:连接OA,
∵∠ACB=20°,
∴∠AOD=40°,
∴,
.
(2)证明:,
,
切于点,
,
,
,
,
,
平分.
【点睛】本题考查与圆有关的计算及圆的性质,解题的关键是掌握弧长公式及圆的切线的性质.
21.(1)
(2)
(3)
【分析】(1)分别作的垂直平分线,即可解答;
(2)用中点公式求得的中点,再利用勾股定理即可解答;
(3)旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,据此求出表面积即可.
【详解】(1)解:如图,外接圆的圆心的坐标是,
故答案为:;
(2)解:根据中点公式,可得的中点,
(3)解:旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,
则他们的母线长为,,
所得表面积为.
【点睛】本题考查了外接圆、两点之间的距离公式、圆锥表面积公式,勾股定理,正确得到旋转后的图形是解题的关键.
22.112cm2.
【分析】根据圆锥的侧面积S=LR==,公式求即可.
【详解】解:∵圆锥的底面周长为30cm,母线长为7cm,
∴圆锥的侧面积为:
答:所需油毡的面积至少是105cm2.
23.ln mile约等于1852m.
【分析】先把1分化为度,再根据弧长公式得到1n mile的长度,然后进行近似计算即可.
【详解】解:∵1’=()°,
∴赤道所在的圆中的圆心角所对的弧长l==≈1.8520(km)=1852m,
∴ln mile约等于1852m
【点睛】本题考查了弧长的计算:弧长公式:熟记弧长公式是解题的关键.
24.28.26m.
【分析】先计算从上午9时到下午6时时针走过的圆心角度数,再由弧长公式求得圆弧的长.
【详解】钟时针长为半径,从上午9时到当天下午6时指针走过270度.
所以时针的针尖走过的路程是28.26m.
【点睛】本题考查圆心角、弧长公式等知识,是重要考点,熟记公式、掌握相关知识是解题关键.
3.9弧长及扇形的面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
2.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是
A.4π B.8π C.12π D.16π
3.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
4.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
5.用一个圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的高为( )
A. B. C. D.
6.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B.1 C. D.4
7.“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
8.一个扇形的半径为60cm,圆心角为120°,用它做一个圆锥的侧面,则圆锥的底面半径为
A.5cm B.10cm C.20cm D.30cm
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆形的半径为1,扇形的圆心角等于,则这个扇形的半径的值是( )
A.3 B.6 C.9 D.12
10.如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
A. B. C. D.
11.如图,四个三角形拼成一个风车图形,若,当风车转动,点B运动的路径长度为( )
A. B. C. D.
12.用圆心角为,半径为的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
A. B. C. D.
二、填空题
13.一个圆锥形零件经过轴的剖面是一个等边三角形,若它的高为5cm,则它的全面积等于 ;
14.如图,将绕点A逆时针旋转得,已知,,那么图中阴影部分的面积是 .(结果保留)
15.已知圆锥的母线长是10cm,侧面展开图的面积是60πcm2,则这个圆锥的底面半径是 cm.
16.若一个圆锥的底面圆的半径为2,母线长为3,则该圆锥侧面展开图的圆心角是 °.
17.如图,已知在扇形中,,半径.P为弧上的动点,过点P作于点M,于点N,点M,N分别在半径上,连接.点D是的外心,则点D运动的路径长为 .
三、解答题
18.如图,已知AB是⊙O的直径,C,D是⊙O上的点,,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
19.如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.
(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;
(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立 请说明理由;
(3)当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.
20.如图,半径为6的⊙O与Rt△ABC的边AB相切于点A,交边BC于点C,D,∠B=90°,连接OD,AD.
(1)若∠ACB=20°,求的长(结果保留).
(2)求证:AD平分∠BDO.
21.如图,在平面直角坐标系中,已知的三个顶点的坐标分别为.
(1)外接圆的圆心的坐标是______;
(2)求该圆圆心到弦的距离;
(3)以所在直线为旋转轴,将旋转一周,求所得几何体的表面积.
22.如图,粮仓的顶部是圆锥形,这个圆锥的底面周长为30cm,母线长为7cm,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是多少
23.在航海中,常用海里(单位:)作为路程的度量单位,把地球看作球体,近似等于赤道所在的圆中的圆心角所对的弧长,已知地球半径(也就是赤道所在圆的半径)约为约等于多少米(取3.14,结果取整数)?
24.上海外滩海关大钟时针长约为6米,从上午9时到当天下午6时,时针的针尖走过的路程是多少米?(取π=3.14)
《3.9弧长及扇形的面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C B B C C B B
题号 11 12
答案 D B
1.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
【详解】连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
【点睛】本题考查动点的运动轨迹问题,根据定弦定角确定圆的所在位置,以及等腰三角形的性质、中位线的性质、弧长公式,熟练掌握这些性质是解题的关键.
2.C
【分析】利用圆锥的侧面展开图为一扇形,再根据扇形的半径等于圆锥的母线长和扇形的面积公式计算.
【详解】解:该扇形的面积.
故选C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长
3.B
【分析】先求出该扇形的半径,再求其面积即可;
【详解】解:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
【点睛】本题主要考查扇形面积的求解,掌握扇形面积的求解公式是解题的关键.
4.C
【分析】根据弧长公式:l=(弧长为l,圆心角度数为n,圆的半径为R),代入即可求出圆心角的度数.
【详解】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
【点睛】本题考查了弧长的计算,解答本题关键是熟练掌握弧长的计算公式,及公式字母表示的含义.
5.B
【分析】根据题意直接利用圆锥的性质求出圆锥的半径,进而利用勾股定理得出圆锥的高.
【详解】解:设此圆锥的底面半径为r,由题意得:,
解得r=2cm,
故这个圆锥的高为:.
故选:B.
【点睛】本题主要考查圆锥的计算,熟练掌握圆锥的性质并正确得出圆锥的半径是解题关键.
6.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.设这个圆锥的底面圆半径为,利用弧长公式得到,然后解关于的方程即可.
【详解】解:设这个圆锥的底面圆半径为,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故选:B
7.C
【详解】∵底面圆的直径为8cm,高为3cm,
∴母线长为5cm,
∴其表面积=π×4×5+42×π+8π×6=84πcm2,
故选C.
8.C
【详解】试题分析:因为扇形的半径为60cm,圆心角为120°,所以扇形的弧长为,而扇形的弧长即为圆锥的底面周长,所以圆锥的底面半径为(cm)
考点:扇形和圆锥的转换关系
点评:扇形的弧长公式为,圆锥底面半径为
9.B
【分析】根据扇形的弧长与圆的周长相等,列方程求解即可.
【详解】解:由题意可得:,解得,
故选:B
【点睛】本题考查扇形弧长公式,圆的周长,掌握扇形弧长公式,圆的周长公式,抓住扇形弧长与圆的周长相等构造等式是解题关键.
10.B
【分析】根据三视图得到此几何体为圆锥,几何体的表面积=侧面积+底面面积,然后根据圆锥的侧面展开图为一扇形,求侧面积扇形面积=,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,底面利用圆的面积求解即可.
【详解】解:该几何体的表面积.
故选:B.
【点睛】本题考查了圆锥表面积的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图的识别.
11.D
【分析】根据题意可知:B点的运动路径是以A点为圆心,长为半径,风车转动的圆弧,计算即可.
【详解】解:,风车转动,
,
故选:D.
【点睛】本题考查了弧长的计算,解题的关键是掌握弧长公式:.
12.B
【分析】本题主要考查了扇形面积的计算.先求出扇形的弧长,根据扇形的弧长=圆锥的底面周长,用扇形的弧长,可求圆锥的底面半径,利用勾股定理得出答案.
【详解】解:∵扇形的弧长,
∴圆锥的底面半径为,
∴这个圆锥形筒的高为.
故选:B.
13.75πcm2
【分析】全面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【详解】圆锥的轴的剖面是一个等边三角形,它的高为cm,
则等边三角形的边长为10 cm,则底面半径=5cm,底面周长=10πcm,
底面面积=25πcm2,侧面面积=50πcm2,
∴圆锥的全面积=25π+50π=75πcm2.
故答案为75πcm2.
【点睛】圆锥是由一个底面和一个侧面围成的图形,我们把圆锥底面圆周上任意一点与圆锥顶点的连线叫做圆锥的母线,连接顶点与底面圆心的线段叫做圆锥的高.沿着圆锥的母线,把圆锥的侧面展开,得到一个扇形,这个扇形的弧长等于圆锥底面圆的周长,而扇形的半径等于圆锥的母线长.
14.
【分析】根据旋转的性质可以得到阴影部分的面积=扇形DAB的面积-扇形EAC的面积,利用扇形的面积公式即可求解.
【详解】解:∵将绕点A逆时针旋转得,
∴S△ABC= S△ADE,
∴阴影部分的面积=扇形DAB的面积+S△ADE -扇形EAC的面积-S△ABC
=扇形DAB的面积-扇形EAC的面积
∴阴影部分的面积,
故答案为:.
【点睛】本题考查了旋转的性质以及扇形的面积公式,根据旋转的性质推出:阴影部分的面积=扇形DAB的面积-扇形EAC的面积是解题关键.
15.6
【分析】圆锥的侧面积公式:圆锥的侧面积=π×母线×底面半径.
【详解】解:设圆锥的底面半径为R,由题意得
π×10R=60π,
解得R=6
则这个圆锥的底面半径是6cm.
【点睛】本题是圆锥的侧面积公式的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.
16.240
【分析】本题考查了圆锥的计算:理解圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键.
【详解】圆锥侧面展开图的弧长是,
设圆心角的度数是,则,
解得,
故答案为:.
17..
【分析】根据点在弧上运动,其路径也是一段弧,由题意可得,点运动路径所对的圆心角是,连接,取的中点,连接,,根据在和中,点是斜边的中点,可证得点,,,四点均在同一个圆,即上,过点作,垂足为点,由垂径定理,,,可求得,再根据点和点重合,得到点运动路径所对的圆心角是,根据弧长公式可求解.
【详解】解:点在弧上运动,其路径也是一段弧,由题意可知,
当点与点重合时,,
当点与点重合时,,
点运动路径所对的圆心角是,
如图,连接,取的中点,连接,,
在和中,点是斜边的中点,
,
根据圆的定义可知,点,,,四点均在同一个圆,即上,
又,,
,,
过点作,垂足为点,
由垂径定理得,,
在中,,,则,
,
∵是的外接圆的圆心,
即:点和点重合,如图2
,
点是以点为圆心为半径,
点运动路径所对的圆心角是,
点运动路径所对的圆心角是,
点运动的路径长为.
故答案是:.
【点睛】本题考查了直径所对的圆周角是直角,弧长公式,三角形的外心的性质,理解题意熟悉公式是解题的关键.
18.(1)证明见解析;(2).
【分析】(1)先根据圆的性质可得,再根据三角形的中位线定理即可得证;
(2)如图(见解析),先根据垂径定理、圆周角定理可得,从而可得,再根据直角三角形的性质、三角形的面积公式可得,然后根据圆周角定理可得,最后根据图中阴影部分的面积等于扇形OAD面积减去面积即可得.
【详解】(1)∵AB是的直径,
∴,即点O是AB的中点,
∵,
∴是的中位线,
点E是AD的中点,
∴;
(2)如图,连接OD,
∵AB是的直径,,
,,
∵,
,即,
又是的半径,
,
,
,,
在中,,
OD是的斜边AB上的中线,
,
又,
,
则图中阴影部分的面积为.
【点睛】本题考查了圆周角定理、垂径定理、扇形的面积公式、三角形中位线定理等知识点,较难的是题(2),熟练掌握圆周角定理和扇形的面积公式是解题关键.
19.(1)详见解析;(2)成立,理由详见解析;(3)+-.
【分析】(1)PN 与⊙O 相切.要证明ON⊥ PN即可,连接ON,PM=PN,所以∠PNM=∠PMN,∠AMO=∠PMN,AB⊥CD,所以∠PMN+∠MAO=90°,又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°,所以PN 与⊙O 相切.
(2)成立,进行等量代换,∠MAO+∠OMA=90°,因∠OMA=∠PNM,∠MAO=∠ONA,所以∠PNM+∠ONA=90°,所以∠ONP=90°;
(3)阴影部分的面积可通过S △AOC+S扇形AOC-S△ AON求得.
【详解】 (1)PN 与⊙O 相切.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
又∵∠AMO=∠PMN,
∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°,
即PN 与⊙O 相切.
(2)成立.理由如下:连接ON,则∠ONA=∠OAN.
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,∠OMA+∠OAM=90°.
∴∠PNM+∠ONA=90°,
∴∠PNO=180°-90°=90°.
即PN 与⊙O 相切.
(3)连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,
∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
过点N 作NE⊥OD,垂足为点E.则OE=.
∴NE=.
∴S阴影=S△AOC+S扇形AON-S△CON=OC·OA+-CO·NE
=+-
∴图中阴影部分的面积为+-
20.(1)
(2)见解析
【分析】(1)连接,由,得,由弧长公式即得的长为;
(2)根据切于点,,可得,有,而,即可得,从而平分.
【详解】(1)解:连接OA,
∵∠ACB=20°,
∴∠AOD=40°,
∴,
.
(2)证明:,
,
切于点,
,
,
,
,
,
平分.
【点睛】本题考查与圆有关的计算及圆的性质,解题的关键是掌握弧长公式及圆的切线的性质.
21.(1)
(2)
(3)
【分析】(1)分别作的垂直平分线,即可解答;
(2)用中点公式求得的中点,再利用勾股定理即可解答;
(3)旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,据此求出表面积即可.
【详解】(1)解:如图,外接圆的圆心的坐标是,
故答案为:;
(2)解:根据中点公式,可得的中点,
(3)解:旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,
则他们的母线长为,,
所得表面积为.
【点睛】本题考查了外接圆、两点之间的距离公式、圆锥表面积公式,勾股定理,正确得到旋转后的图形是解题的关键.
22.112cm2.
【分析】根据圆锥的侧面积S=LR==,公式求即可.
【详解】解:∵圆锥的底面周长为30cm,母线长为7cm,
∴圆锥的侧面积为:
答:所需油毡的面积至少是105cm2.
23.ln mile约等于1852m.
【分析】先把1分化为度,再根据弧长公式得到1n mile的长度,然后进行近似计算即可.
【详解】解:∵1’=()°,
∴赤道所在的圆中的圆心角所对的弧长l==≈1.8520(km)=1852m,
∴ln mile约等于1852m
【点睛】本题考查了弧长的计算:弧长公式:熟记弧长公式是解题的关键.
24.28.26m.
【分析】先计算从上午9时到下午6时时针走过的圆心角度数,再由弧长公式求得圆弧的长.
【详解】钟时针长为半径,从上午9时到当天下午6时指针走过270度.
所以时针的针尖走过的路程是28.26m.
【点睛】本题考查圆心角、弧长公式等知识,是重要考点,熟记公式、掌握相关知识是解题关键.
