3.8圆内接正多边形同步练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 3.8圆内接正多边形同步练习 北师大版数学九年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 06:01:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.8圆内接正多边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
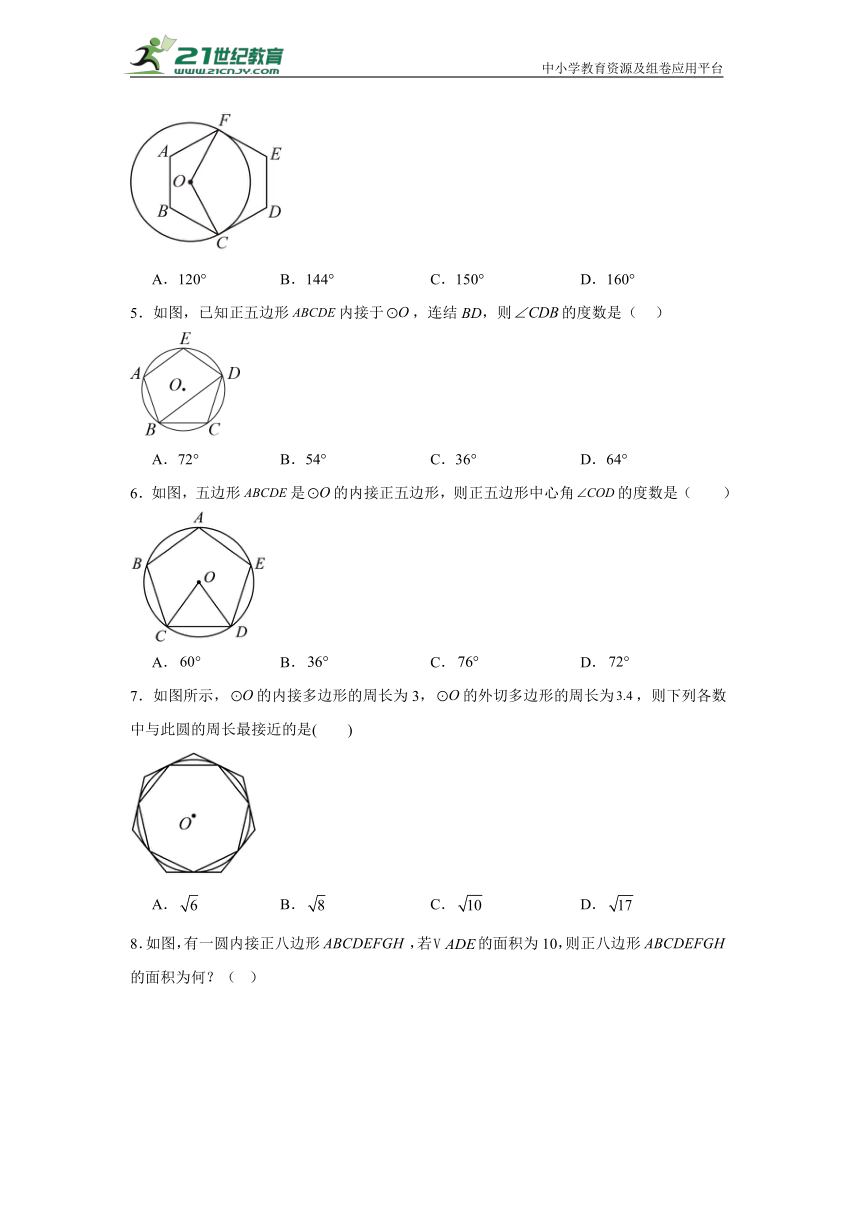
1.如图,四边形 ABCD 内接于⊙O,若∠C=36°,则∠A 的度数为( )
A.36° B.56° C.72° D.144°
2.如图,连接的内接正十二边形顶点得到,,若,则阴影部分的面积为( )
A. B.2 C. D.
3.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
A.35° B.70° C.110° D.140°
4.如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
5.如图,已知正五边形内接于,连结BD,则的度数是( )
A.72° B.54° C.36° D.64°
6.如图,五边形是的内接正五边形,则正五边形中心角的度数是( )
A. B. C. D.
7.如图所示,的内接多边形的周长为3,的外切多边形的周长为,则下列各数中与此圆的周长最接近的是( )
A. B. C. D.
8.如图,有一圆内接正八边形,若的面积为10,则正八边形的面积为何?( )
A.40 B.50 C.60 D.80
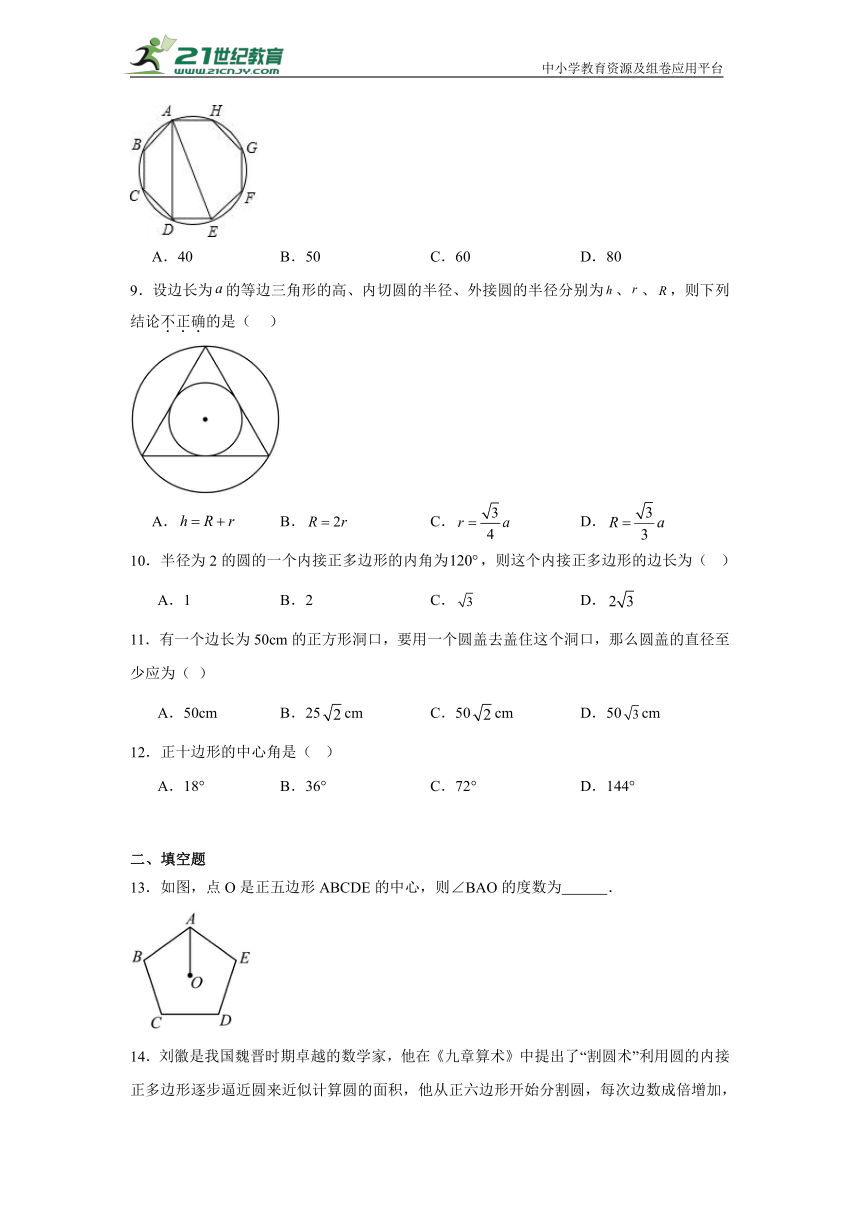
9.设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
10.半径为2的圆的一个内接正多边形的内角为,则这个内接正多边形的边长为( )
A.1 B.2 C. D.
11.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.50cm B.25cm C.50cm D.50cm
12.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
二、填空题
13.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为 .
14.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,他从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形……割的越细,圆的内接正多边形就越接近圆.如图,若用圆的内接正十二边形的面积S1,来近似估计⊙O的面积S,设正十二边形边长为1,则S1= ; .
15.一个正多边形的一个外角为30°,则它的内角和为 .
16.如果一个正多边形的中心角等于,那么这个正多边形的对称轴共有 条.
17.正十二边形的每一个外角为 ,每一个内角是 ,该图形绕其中心至少旋转 才能和本身重合.
三、解答题
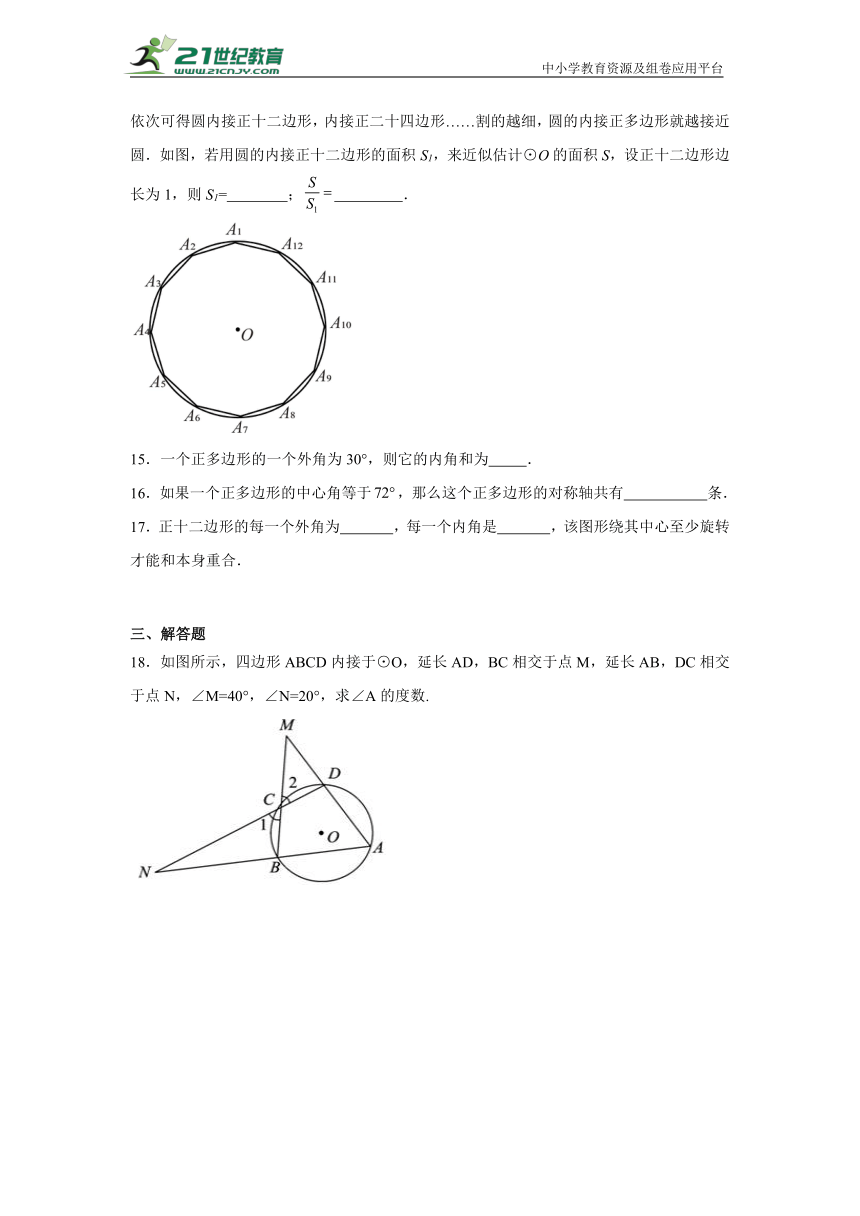
18.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
19.用一批全长为的篱笆围出一块草地,分别计算所围草地是正三角形、正方形、正六边形和圆时的面积(精确到),并比较它们的大小.
20.如图,在□ABCD中,∠BAD为钝角,且AE⊥BC,A F⊥CD.
(1) 求证:A、E、C、F四点共圆;
(2) 设线段 BD与(1)中的圆交于M、N.求证:BM = ND
21.已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
22.在圆内接四边形中,,,的度数比是,求四边各内角的度数.
23.正六边形的边长为8,求这个正六边形的周长和面积.
24.如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________.
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
《3.8圆内接正多边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A C D C A C B
题号 11 12
答案 C B
1.D
【分析】根据圆的内接四边形的对角互补得到∠A+∠C=180°,把∠C=36°代入计算即可.
【详解】∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
而∠C=36°,
∴∠A=180°-36°=144°
故选D.
【点睛】考查了圆的内接四边形的性质:圆内接四边形对角互补.
2.B
【分析】根据已知条件得到,求得,,得到,过作于,于,解直角三角形得到,,根据梯形的面积公式即可得到结论.
【详解】解:如图所示,
,
,,
,
,
过作于,于,
,
,
,
,
,
,
,
阴影部分的面积为.
故选:B.
【点睛】本题考查了正多边形与圆,梯形的面积的计算,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.
3.D
【分析】由圆内接四边形的外角等于它的内对角知,∠A=∠DCE=70°,由圆周角定理知,∠BOD=2∠A=140°.
【详解】∵四边形ABCD内接于⊙O,
∴∠A=∠DCE=70°,
∴∠BOD=2∠A=140°.
故选D.
4.A
【分析】本题考查正多边形和圆,切线的性质,掌握正六边形的性质,切线的性质以及多边形内角和的计算方法是正确解答的关键.根据正六边形的性质可求出各个内角的度数,由切线的性质以及五边形内角和的计算方法即可求出答案.
【详解】解:∵正六边形的边,与相切于点C,F,
∴,
∵六边形是正六边形,
∴,
在五边形中,
,
故选:A.
5.C
【分析】连接、,先求出正五边形的中心角,再根据圆周角知识即可求出.
【详解】解:连接,如图,
∵正五边形内接于,
∴,
∵,
∴.
故选:C
【点睛】本题考查了求正五边形的中心角,圆周角定理等知识,熟知相关知识,求出正五边形的中心角是解题关键.
6.D
【分析】根据正多边形的中心角的计算公式:计算即可.
【详解】解:∵五边形是的内接正五边形,
∴五边形的中心角的度数为,
故选D.
【点睛】本题考查圆内接正多边形的中心角.熟练掌握正多边形的中心角的计算公式:,是解题的关键.
7.C
【分析】根据圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长.圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,然后把3与3.4平方,再利用夹逼法对即可选择答案.
【详解】解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长,
圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,
,
圆的周长,
只有C选项满足条件.
故选:C.
【点睛】本题考查了正多边形和圆,解题关键是熟悉正多边形和圆的关系.
8.A
【分析】取中点I,则点I为圆的圆心,圆内接正八边形是由8个与全等的三角形构成,从而可得答案.
【详解】解:取中点I,则点I为圆的圆心,
圆内接正八边形是由8个与全等的三角形构成.
∵的面积为10,
∴的面积为5,则圆内接正八边形为.
故选A.
【点睛】本题考查的是正多边形与圆,掌握“正多边形的性质”是解本题的关键.
9.C
【分析】将图形标记各点,即可从图中看出长度关系证明A正确,再由构造的直角三角形和30°特殊角证明B正确,利用勾股定理求出r和R,即可判断C、D.
【详解】
如图所示,标上各点,AO为R,OB为r,AB为h,
从图象可以得出AB=AO+OB,即,A正确;
∵三角形为等边三角形,
∴∠CAO=30°,
根据垂径定理可知∠ACO=90°,
∴AO=2OC,即R=2r,B正确;
在Rt△ACO中,利用勾股定理可得:AO2=AC2+OC2,即,
由B中关系可得:,解得,则,
所以C错误,D正确;
故选:C.
【点睛】本题考查圆与正三角形的性质结合,关键在于巧妙利用半径和构建直角三角形.
10.B
【分析】本题考查正多边形和圆,掌握正六边形的性质是正确解答的前提.
根据正六边形的性质,正三角形的性质进行计算即可.
【详解】解:如图,
∵半径为2的圆的一个内接正多边形的内角为,
∴,
∴,
∴的内接正多边形是六边形,
,
,
∴是正三角形,
,
∴正六边形的边长为2,
故选:B.
11.C
【详解】解:要用一个圆盖去盖住一个正方形的洞口,则圆盖的直径至少应为正方形的对角线的长,∵正方形边长为50cm,
由勾股定理可得正方形的对角线的长为:50cm.
故答案选C.
12.B
【分析】正多边形的每个中心角相等,且其和是360°,故一个中心角的度数为360°除以正多边形的边数.
【详解】正十边形的每个中心角相等,且其和是360°,故一个中心角的度数为:360°÷10=36°
故选:B
【点睛】本题考查了求正多边形中心角,这时要清楚正多边形的中心角都相等且它们的和组成一个周角.
13.54°/54度
【详解】解:连接OB,则OB=OA,
∴∠BAO=∠ABO,
∵点O是正五边形ABCDE的中心,
∴∠AOB=360°÷5=72°,
∴∠BAO=(180°﹣72°)=54°;
故答案为54°.
14. 6+3
【分析】连接OA1、OA2,过A1作A1H⊥OA2于H,设A1H=x,在Rt△A1A2H中,可得x2+(2x-x)2=12,解出x的值,即可求出S、S1,从而得到答案.
【详解】解:连接OA1、OA2,过A1作A1H⊥OA2于H,如图:
∵圆的内接正十二边形的中心角为=30°,
∴∠A1OH=30°,
∴A1H=OA1,
设A1H=x,则OA1=2x=OA2,OH=A1H,
∴A2H=2x-x,
在Rt△A1A2H中,A2H2+A1H2=A1A22,
∴x2+(2x-x)2=12,
解得x=(负值已舍去),
∴A1H=,OA1=,
∴S=π×()2=(2+)π,
S1=12×××=6+3,
∴,
故答案为:6+3,.
【点睛】本题考查了正多边形与圆,正确地求出正十二边形的面积是解题的关键.
15.1800°
【详解】解:根据题意得:这个正多边形的边数为=12,
所以这个正多边形的内角和为(12﹣2)×180°=1800°.
故答案为1800°.
16.
【分析】本题考查了正多边形与圆,对称轴数量问题,先求得正多边形的边数,进而根据对称性求得对称轴数量,即可求解.
【详解】解:设这个多边形的边数为,∵中心角的度数=,
,,
∴这个正多边形为正五边形,每个顶点与其对边中点的连线所在的直线为对称轴,共5条对称轴,
故答案为:.
17. 30° 150° 30°
【分析】根据多边形内角和公式可得正十二边形的内角和为1800°,因为正十二边形有12个内角,且每个内角都相等,所以每个内角的度数为1800°÷12=150°;每个外角和每个内角都是互补的关系即可得到每个外角的度数.
【详解】易得正十二边形的内角和为1800°,故其每个内角为1800°÷12=150°;
由多边形外角与内角互补可得其每个外角的度数为180°-150°=30°;
因为正十二边形的中心角为=30°,
所以正十二边形绕其中心经过旋转与原图重合,则要至少旋转的度数为30°.
【点睛】本题考查了多边形的内角和和外角,解题的关键是内角和与边数成正比,边数增加,内角和增加;边数减少,内角和减少.每增加一条边,内角和就增加180°.
18.∠A=60°.
【分析】根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
19.正三角形的面积为平方米,正方形的面积为平方米,正六边形的面积为平方米,圆的面积为平方米,
【分析】本题考查了等边三角形的性质,勾股定理,正多边形的性质.熟练掌握等边三角形的性质,勾股定理,正多边形的性质是解题的关键.
先根据周长求正三角形,正方形,正六边形的边长,圆的半径,然后求高,求面积,最后比大小即可.
【详解】解:由题意可得,正三角形的边长为,
∴正三角形底边上的高为;
∴;
∵正方形的边长为,
∴,
∵正六边形的边长为,
∴边心距为,
∴;
∵圆的半径,
∴;
∵,
∴在周长都是时,.
20.(1)见解析;(2)见解析.
【分析】(1)只要证明A、E、C、F四点所构成的四边形的对角互补,则该四点共圆;
(2)连接AC交BD于O,易得O是该圆的圆心,OM=ON,所以可得BM=ND.
【详解】(1)∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠AEC+∠AFC=180°,
∴A、E、C、F四点共圆;
(2)由(1)可知,圆的直径是AC,
连接AC交BD于O,
∵ABCD是平行四边形,
∴O为圆心,OB=OD,
∴OM=ON,
∴BM=ND.
【点睛】本题主要考查了四点共圆的判定及平行四边形的性质,难度不大,能够灵活运用所学知识进行推理是解题关键..
21.证明见解析
【详解】试题分析:要求证五边形AEBCF是正五边形,就是证明这个五边形的五条边所对的弧相等进而得出即可.
试题解析:
连接BF,CE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵AB、AC的中垂线分别交⊙O于点E、F,
∴AF=CF,AE=BE,
∴∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36°,
∴ ,
∴AE=AF=BE=BC=FC,
∴∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴五边形AEBCF为正五边形.
22.四边形各内角的度数分别是,,,.
【分析】设,,,由圆内接四边形的性质可得,得到x,再由圆周角定理得到答案.
【详解】依题意,设,,,
∴,∴.
∴,,.
∴.
∴四边形各内角的度数分别是,,,.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
23.周长,面积
【分析】本题主要考查了正六边形的性质,根据正多边形的性质,得出为等边三角形,即可解答.解题的关键是掌握正多边形每条边相等,以及中心角的求法.
【详解】解:正六边形的周长;
连接,过点O作于点G,
∵该六边形为正六边形,
∴,
∴为等边三角形,
∴,,
∵,
正六边形的面积.
24.(1)60°;(2)90°,108°;(3).
【分析】根据对顶角相等和三角形内角和外角的关系解答即可.
【详解】解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
(2)同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
【点睛】此题是一道规律探索题,体现了探索发现的一般规律:通过计算得出特殊多边形中的角∠APN的度数,然后得出n边形的∠APN的度数.
3.8圆内接正多边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形 ABCD 内接于⊙O,若∠C=36°,则∠A 的度数为( )
A.36° B.56° C.72° D.144°
2.如图,连接的内接正十二边形顶点得到,,若,则阴影部分的面积为( )
A. B.2 C. D.
3.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
A.35° B.70° C.110° D.140°
4.如图,正六边形的边,与相切于点C,F,连接,,则的度数是( )
A.120° B.144° C.150° D.160°
5.如图,已知正五边形内接于,连结BD,则的度数是( )
A.72° B.54° C.36° D.64°
6.如图,五边形是的内接正五边形,则正五边形中心角的度数是( )
A. B. C. D.
7.如图所示,的内接多边形的周长为3,的外切多边形的周长为,则下列各数中与此圆的周长最接近的是( )
A. B. C. D.
8.如图,有一圆内接正八边形,若的面积为10,则正八边形的面积为何?( )
A.40 B.50 C.60 D.80
9.设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
10.半径为2的圆的一个内接正多边形的内角为,则这个内接正多边形的边长为( )
A.1 B.2 C. D.
11.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.50cm B.25cm C.50cm D.50cm
12.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
二、填空题
13.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为 .
14.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,他从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形……割的越细,圆的内接正多边形就越接近圆.如图,若用圆的内接正十二边形的面积S1,来近似估计⊙O的面积S,设正十二边形边长为1,则S1= ; .
15.一个正多边形的一个外角为30°,则它的内角和为 .
16.如果一个正多边形的中心角等于,那么这个正多边形的对称轴共有 条.
17.正十二边形的每一个外角为 ,每一个内角是 ,该图形绕其中心至少旋转 才能和本身重合.
三、解答题
18.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
19.用一批全长为的篱笆围出一块草地,分别计算所围草地是正三角形、正方形、正六边形和圆时的面积(精确到),并比较它们的大小.
20.如图,在□ABCD中,∠BAD为钝角,且AE⊥BC,A F⊥CD.
(1) 求证:A、E、C、F四点共圆;
(2) 设线段 BD与(1)中的圆交于M、N.求证:BM = ND
21.已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
22.在圆内接四边形中,,,的度数比是,求四边各内角的度数.
23.正六边形的边长为8,求这个正六边形的周长和面积.
24.如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________.
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
《3.8圆内接正多边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A C D C A C B
题号 11 12
答案 C B
1.D
【分析】根据圆的内接四边形的对角互补得到∠A+∠C=180°,把∠C=36°代入计算即可.
【详解】∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
而∠C=36°,
∴∠A=180°-36°=144°
故选D.
【点睛】考查了圆的内接四边形的性质:圆内接四边形对角互补.
2.B
【分析】根据已知条件得到,求得,,得到,过作于,于,解直角三角形得到,,根据梯形的面积公式即可得到结论.
【详解】解:如图所示,
,
,,
,
,
过作于,于,
,
,
,
,
,
,
,
阴影部分的面积为.
故选:B.
【点睛】本题考查了正多边形与圆,梯形的面积的计算,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.
3.D
【分析】由圆内接四边形的外角等于它的内对角知,∠A=∠DCE=70°,由圆周角定理知,∠BOD=2∠A=140°.
【详解】∵四边形ABCD内接于⊙O,
∴∠A=∠DCE=70°,
∴∠BOD=2∠A=140°.
故选D.
4.A
【分析】本题考查正多边形和圆,切线的性质,掌握正六边形的性质,切线的性质以及多边形内角和的计算方法是正确解答的关键.根据正六边形的性质可求出各个内角的度数,由切线的性质以及五边形内角和的计算方法即可求出答案.
【详解】解:∵正六边形的边,与相切于点C,F,
∴,
∵六边形是正六边形,
∴,
在五边形中,
,
故选:A.
5.C
【分析】连接、,先求出正五边形的中心角,再根据圆周角知识即可求出.
【详解】解:连接,如图,
∵正五边形内接于,
∴,
∵,
∴.
故选:C
【点睛】本题考查了求正五边形的中心角,圆周角定理等知识,熟知相关知识,求出正五边形的中心角是解题关键.
6.D
【分析】根据正多边形的中心角的计算公式:计算即可.
【详解】解:∵五边形是的内接正五边形,
∴五边形的中心角的度数为,
故选D.
【点睛】本题考查圆内接正多边形的中心角.熟练掌握正多边形的中心角的计算公式:,是解题的关键.
7.C
【分析】根据圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长.圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,然后把3与3.4平方,再利用夹逼法对即可选择答案.
【详解】解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长,
圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,
,
圆的周长,
只有C选项满足条件.
故选:C.
【点睛】本题考查了正多边形和圆,解题关键是熟悉正多边形和圆的关系.
8.A
【分析】取中点I,则点I为圆的圆心,圆内接正八边形是由8个与全等的三角形构成,从而可得答案.
【详解】解:取中点I,则点I为圆的圆心,
圆内接正八边形是由8个与全等的三角形构成.
∵的面积为10,
∴的面积为5,则圆内接正八边形为.
故选A.
【点睛】本题考查的是正多边形与圆,掌握“正多边形的性质”是解本题的关键.
9.C
【分析】将图形标记各点,即可从图中看出长度关系证明A正确,再由构造的直角三角形和30°特殊角证明B正确,利用勾股定理求出r和R,即可判断C、D.
【详解】
如图所示,标上各点,AO为R,OB为r,AB为h,
从图象可以得出AB=AO+OB,即,A正确;
∵三角形为等边三角形,
∴∠CAO=30°,
根据垂径定理可知∠ACO=90°,
∴AO=2OC,即R=2r,B正确;
在Rt△ACO中,利用勾股定理可得:AO2=AC2+OC2,即,
由B中关系可得:,解得,则,
所以C错误,D正确;
故选:C.
【点睛】本题考查圆与正三角形的性质结合,关键在于巧妙利用半径和构建直角三角形.
10.B
【分析】本题考查正多边形和圆,掌握正六边形的性质是正确解答的前提.
根据正六边形的性质,正三角形的性质进行计算即可.
【详解】解:如图,
∵半径为2的圆的一个内接正多边形的内角为,
∴,
∴,
∴的内接正多边形是六边形,
,
,
∴是正三角形,
,
∴正六边形的边长为2,
故选:B.
11.C
【详解】解:要用一个圆盖去盖住一个正方形的洞口,则圆盖的直径至少应为正方形的对角线的长,∵正方形边长为50cm,
由勾股定理可得正方形的对角线的长为:50cm.
故答案选C.
12.B
【分析】正多边形的每个中心角相等,且其和是360°,故一个中心角的度数为360°除以正多边形的边数.
【详解】正十边形的每个中心角相等,且其和是360°,故一个中心角的度数为:360°÷10=36°
故选:B
【点睛】本题考查了求正多边形中心角,这时要清楚正多边形的中心角都相等且它们的和组成一个周角.
13.54°/54度
【详解】解:连接OB,则OB=OA,
∴∠BAO=∠ABO,
∵点O是正五边形ABCDE的中心,
∴∠AOB=360°÷5=72°,
∴∠BAO=(180°﹣72°)=54°;
故答案为54°.
14. 6+3
【分析】连接OA1、OA2,过A1作A1H⊥OA2于H,设A1H=x,在Rt△A1A2H中,可得x2+(2x-x)2=12,解出x的值,即可求出S、S1,从而得到答案.
【详解】解:连接OA1、OA2,过A1作A1H⊥OA2于H,如图:
∵圆的内接正十二边形的中心角为=30°,
∴∠A1OH=30°,
∴A1H=OA1,
设A1H=x,则OA1=2x=OA2,OH=A1H,
∴A2H=2x-x,
在Rt△A1A2H中,A2H2+A1H2=A1A22,
∴x2+(2x-x)2=12,
解得x=(负值已舍去),
∴A1H=,OA1=,
∴S=π×()2=(2+)π,
S1=12×××=6+3,
∴,
故答案为:6+3,.
【点睛】本题考查了正多边形与圆,正确地求出正十二边形的面积是解题的关键.
15.1800°
【详解】解:根据题意得:这个正多边形的边数为=12,
所以这个正多边形的内角和为(12﹣2)×180°=1800°.
故答案为1800°.
16.
【分析】本题考查了正多边形与圆,对称轴数量问题,先求得正多边形的边数,进而根据对称性求得对称轴数量,即可求解.
【详解】解:设这个多边形的边数为,∵中心角的度数=,
,,
∴这个正多边形为正五边形,每个顶点与其对边中点的连线所在的直线为对称轴,共5条对称轴,
故答案为:.
17. 30° 150° 30°
【分析】根据多边形内角和公式可得正十二边形的内角和为1800°,因为正十二边形有12个内角,且每个内角都相等,所以每个内角的度数为1800°÷12=150°;每个外角和每个内角都是互补的关系即可得到每个外角的度数.
【详解】易得正十二边形的内角和为1800°,故其每个内角为1800°÷12=150°;
由多边形外角与内角互补可得其每个外角的度数为180°-150°=30°;
因为正十二边形的中心角为=30°,
所以正十二边形绕其中心经过旋转与原图重合,则要至少旋转的度数为30°.
【点睛】本题考查了多边形的内角和和外角,解题的关键是内角和与边数成正比,边数增加,内角和增加;边数减少,内角和减少.每增加一条边,内角和就增加180°.
18.∠A=60°.
【分析】根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
19.正三角形的面积为平方米,正方形的面积为平方米,正六边形的面积为平方米,圆的面积为平方米,
【分析】本题考查了等边三角形的性质,勾股定理,正多边形的性质.熟练掌握等边三角形的性质,勾股定理,正多边形的性质是解题的关键.
先根据周长求正三角形,正方形,正六边形的边长,圆的半径,然后求高,求面积,最后比大小即可.
【详解】解:由题意可得,正三角形的边长为,
∴正三角形底边上的高为;
∴;
∵正方形的边长为,
∴,
∵正六边形的边长为,
∴边心距为,
∴;
∵圆的半径,
∴;
∵,
∴在周长都是时,.
20.(1)见解析;(2)见解析.
【分析】(1)只要证明A、E、C、F四点所构成的四边形的对角互补,则该四点共圆;
(2)连接AC交BD于O,易得O是该圆的圆心,OM=ON,所以可得BM=ND.
【详解】(1)∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠AEC+∠AFC=180°,
∴A、E、C、F四点共圆;
(2)由(1)可知,圆的直径是AC,
连接AC交BD于O,
∵ABCD是平行四边形,
∴O为圆心,OB=OD,
∴OM=ON,
∴BM=ND.
【点睛】本题主要考查了四点共圆的判定及平行四边形的性质,难度不大,能够灵活运用所学知识进行推理是解题关键..
21.证明见解析
【详解】试题分析:要求证五边形AEBCF是正五边形,就是证明这个五边形的五条边所对的弧相等进而得出即可.
试题解析:
连接BF,CE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵AB、AC的中垂线分别交⊙O于点E、F,
∴AF=CF,AE=BE,
∴∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36°,
∴ ,
∴AE=AF=BE=BC=FC,
∴∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴五边形AEBCF为正五边形.
22.四边形各内角的度数分别是,,,.
【分析】设,,,由圆内接四边形的性质可得,得到x,再由圆周角定理得到答案.
【详解】依题意,设,,,
∴,∴.
∴,,.
∴.
∴四边形各内角的度数分别是,,,.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
23.周长,面积
【分析】本题主要考查了正六边形的性质,根据正多边形的性质,得出为等边三角形,即可解答.解题的关键是掌握正多边形每条边相等,以及中心角的求法.
【详解】解:正六边形的周长;
连接,过点O作于点G,
∵该六边形为正六边形,
∴,
∴为等边三角形,
∴,,
∵,
正六边形的面积.
24.(1)60°;(2)90°,108°;(3).
【分析】根据对顶角相等和三角形内角和外角的关系解答即可.
【详解】解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
(2)同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
【点睛】此题是一道规律探索题,体现了探索发现的一般规律:通过计算得出特殊多边形中的角∠APN的度数,然后得出n边形的∠APN的度数.
