3.2圆的对称性同步练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 3.2圆的对称性同步练习 北师大版数学九年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 786.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 06:20:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.2圆的对称性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图, AB是⊙O的直径, CD是AO的垂直平分线, EF是OB的垂直平分线, 则下列结论正确的是 ( )
A.== B.
C. D.
2.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
3.如图,已知AD=BC,则AB与CD的关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
4.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
5.下列说法正确的是( )
A.长度相等的弧是等弧 B.半圆是弧
C.等弦对等圆心角 D.直径是最长的弦,半径是最短的弦
6.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.相等的圆心角所对的弦相等
C.相等的弧所对的弦相等 D.相等的弦所对的弧相等
7.如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为40°,70°,150°,则∠B的度数是( )
A.20° B.25° C.30° D.35°
8.如图,点A,B,C,D是⊙O上的四个点,且,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B. C. D.
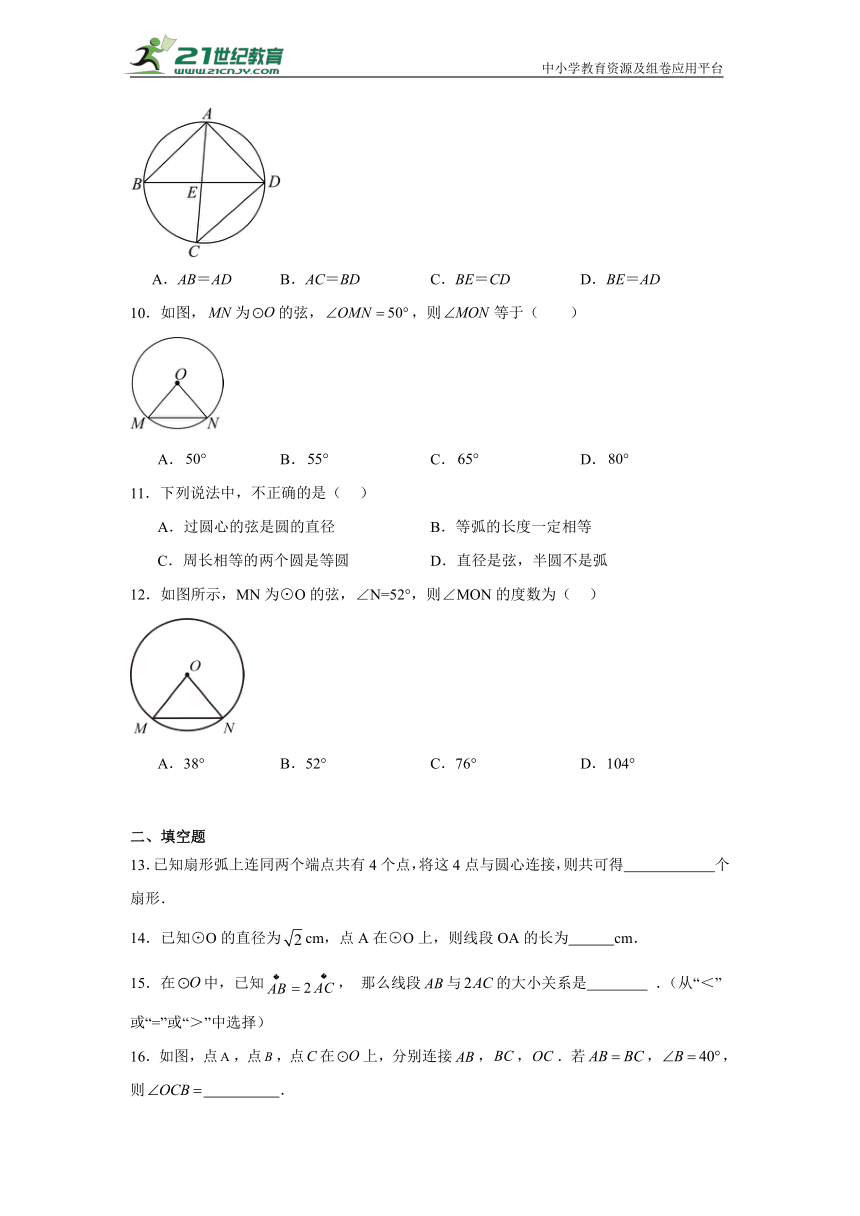
9.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
A.AB=AD B.AC=BD C.BE=CD D.BE=AD
10.如图,为的弦,,则等于( )
A. B. C. D.
11.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
12.如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )
A.38° B.52° C.76° D.104°
二、填空题
13.已知扇形弧上连同两个端点共有4个点,将这4点与圆心连接,则共可得 个扇形.
14.已知⊙O的直径为cm,点A在⊙O上,则线段OA的长为 cm.
15.在中,已知, 那么线段与的大小关系是 .(从“<”或“=”或“>”中选择)
16.如图,点,点,点在上,分别连接,,.若,,则 .
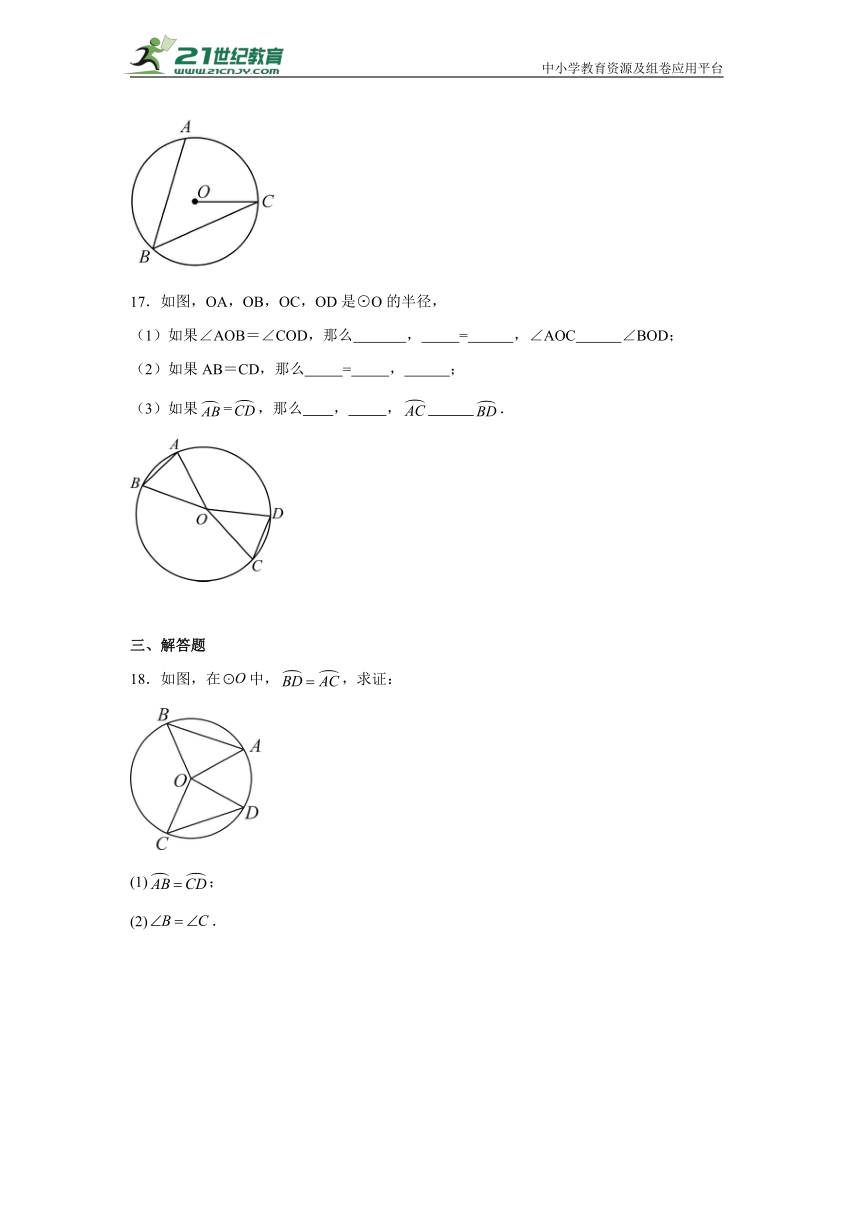
17.如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么 , = ,∠AOC ∠BOD;
(2)如果AB=CD,那么 = , ;
(3)如果=,那么 , , .
三、解答题
18.如图,在中,,求证:
(1);
(2).
19.如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
20.如图,是的直径,点,在上,且点,在的异侧,连接,,.若所对圆心角的度数为70°,且,求所对圆心角的度数.
21.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数
(2)求∠EOD的度数
22.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断和是否相等,并说明理由.
23.利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)是中心对称图形但不是轴对称图形;
(3)既是轴对称图形又是中心对称图形.
24.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.
(1)求证:=;
(2)若C、D分别为OA、OB中点,则成立吗?
《3.2圆的对称性》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A B C A D B D
题号 11 12
答案 D C
1.A
【分析】如图,连接AD,OD,DF,OF,BF,根据垂直平分线的性质易证DF=DF=BF,再根据“在同圆或等圆中,所对的弦相等的两段弧是等弧”即可判断.
【详解】如图,连接AD,OD,DF,OF,BF,
∵CD是AO的垂直平分线, EF是OB的垂直平分线,
∴DF=CE=AB,AD=OD,OF=BF,
∴DF=DF=BF,
则==.
故选A.
【点睛】本题主要考查垂直平分线的性质,等弧的判定,解此题的关键在于熟练掌握其知识点.
2.C
【分析】利用垂径定理分别判断后即可确定正确的选项.
【详解】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
【点睛】本题考查了命题与定理的知识,解题的关键是理解垂径定理及其推理,难度不大.
3.B
【分析】由题知AD=BC,根据圆心角、弧、弦的关系,得出=.
再给=.两边加上,即可得到AB与CD的关系.
【详解】∵AD=BC,
∴=.
∴+=+,
即=.
∴AB=CD.
故选:B.
【点睛】本题考查了圆心角、弧、弦的关系定理,解题关键熟练掌握圆心角、弧、弦的关系定理;
4.A
【详解】试题分析:根据垂径定理即可判断A、B;根据AB和CD可能平行也可能相交,即可判断C;根据对称轴是直线,即可判断D.
解:A、垂直于弦的直径平分弦,且平分弦所对的弧,故本选项正确;
B、平分弦(弦不是直径)直径垂直于弦,并且平分弦所对的弧,故本选项错误;
C、AB和CD可能相交,故本选项错误;
D、圆是轴对称图形,对称轴是圆的每一条直径所在的直线,故本选项错误;
故选A.
点评:本题考查了垂径定理和圆的认识的应用,主要考查学生对定理的理解能力,题目比较典型,但是一道比较容易出错的题目.
5.B
【分析】根据连接圆上任意两点的线段叫弦,经过圆心的弦叫直径;圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆;在同圆或等圆中,等弦所对的弧对应相等,等弧所对的圆心角相等,逐项判断可得答案.
【详解】解:A.等弧指的是在同圆或等圆中,能够互相重合的弧,而不是长度相等,就一定能够重合,故此选项不符合题意;
B.半圆是弧,故此选项符合题意;
C.在同圆或等圆中,等弦所对的弧对应相等,等弧所对的圆心角相等,故此选项不符合题意;
D.直径是最长的弦,半径不是弦,故此选项不符合题意.
故选:B.
【点睛】本题考查圆的认识,在同圆或等圆中,弦,弧,圆心角的关系.解题的关键是掌握弧、半圆和弦的定义,弦、弧、圆心角的关系.
6.C
【分析】首先要明确是否同圆或者等圆,其次还要明确优弧还是劣弧.
【详解】A、B选项中的结论必须要有“同圆或等圆”的前提,故均错误;D选项除了要明确“同圆或等圆”外,还要明确是优弧还是劣弧,故也错误;
故选择C.
【点睛】对于定理,一定不能忽略它的前提和一些限制条件.
7.A
【分析】连结OD,如图,根据题意得∠DOC=30°,∠AOD=80°,由于OD=OA,则∠ADO=50°,然后利用三角形外角性质得∠ADO=∠B+∠DOB,得出∠B=50°-30°=20°即可.
【详解】解:连结OD,如图
则∠DOC=70°-40°=30°,∠AOD=150°-70°=80°,
∵OD=OA,
∴∠ADO=50°,
∵∠ADO=∠B+∠DOB,
∴∠B=50°-30°=20°.
故选A.
【点睛】本题考查圆周角定理、等腰三角形的性质、三角形的外角性质;由等腰三角形的性质得出∠ADO=50°是解题的关键.
8.D
【分析】在同圆中,根据圆心角、弧和弦之间的关系即可判断.
【详解】解:在⊙O中,
∵
∴,
故A、C选项正确,不符合题意;
∵,OA=OD,OB=OC
∴
∴
∵OE⊥AB,OF⊥CD,
∴
∴OE=OF
故B选项正确,不符合题意.
故选D
【点睛】本题考查圆的对称性,理解同圆中圆心角、弧和弦之间的关系是解题的关键.
9.B
【分析】连接BC,根据弧与弦的关系得出,进而判断即可.
【详解】连接BC,
∵
∴
∴
∴AC=BD
故选:B
【点睛】此题考查圆心角、弧、弦的关系,关键是根据弧与弦的关系得出.
10.D
【分析】先运用了等腰三角形的性质求出,再根据三角形的内角和是即可得.
【详解】解:,
为等腰三角形,
,
,
所以.
故选:D.
【点睛】本题考查了等腰三角形的性质,三角形的内角和定理,熟练运用等腰三角形的性质等边对等角是解题的关键.
11.D
【分析】对于A,直径是通过圆心且两个端点都在圆上的线段,即可进行判断;
对于B,能重合的弧叫等弧,即可进行判断;
对于C和D,分别根据等圆,直径,半圆的知识,也可进行判断.
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
【点睛】本题考查圆的认识,解题的关键是掌握弦,弧等知识,灵活运用所学知识解决问题
12.C
【分析】根据半径相等得到OM=ON,则∠M=∠N=52°,然后根据三角形内角和定理计算∠MON的度数.
【详解】∵OM=ON,
∴∠M=∠N=52°,
∴∠MON=180°-2×52°=76°.
故选C.
【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
13.6
【详解】如图,当扇形AOD的上有A、B、C、D四个点时,连接OA、OB、OC、OD,则图中的扇形有:扇形AOD、扇形AOC、扇形AOB、扇形BOD、扇形BOC、扇形COD,共计6个.
故答案为6.
14.
【详解】解:∵⊙O的直径为cm,
∴⊙O的半径为cm,
∵点A在⊙O上,
∴线段OA=cm.
故答案为.
15.
【分析】本题考查的是圆心角、弧、弦的关系、三角形三边关系,根据圆心角、弧、弦的关系定理和三角形三边关系定理解得即可.
【详解】解:∵
∴
∴
在中,
∴
16./20度
【分析】首先连接,,然后根据等弦对等圆心角得到,再根据三角形内角和得到,再由,,即可得到结果.
【详解】解:如图,连接,,
,
,,
,
,
,
,,
.
故答案为:.
【点睛】本题主要考查圆内相关概念和定理,三角形内角和定理等内容;掌握圆内相关概念是解题基础.
17.(1)AB=CD,, , = ;(2) , ,∠AOB=∠COD;(3)AB=CD,∠AOB=∠COD, =
【分析】根据在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等进行解答.
【详解】(1)∵∠AOB=∠COD,
∴AB=CD,,∠AOC=∠BOD;
(2)∵AB=CD,
∴,∠AOB=∠COD;
(3)∵,
∴AB=CD,∠AOB=∠COD,.
故答案为:(1)AB=CD,,,=;(2),,∠AOB=∠COD;(3)AB=CD,∠AOB=∠COD,=.
【点睛】本题考查了圆心角、弧、弦的关系,在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
18.(1)见解析
(2)见解析
【分析】本题考查了圆心角、弧、弦的关系,等腰三角形的性质,解答本题用到的知识点为:同弧所对的圆心角相等,等腰三角形两底角相等等.
(1)由,可知,得到;
(2)根据圆心角、弧、弦的关系由,得到,然后利用等腰三角形底角相等即可得到结论.
【详解】(1)证明:,
;
(2)证明:,
,
又,
,
即.
19.(1)见解析;(2)见解析
【分析】(1)连接BD,根据圆周角定理可得∠ADB=∠CBD,根据平行线的判定可得结论;
(2)证明△DEF≌△BCF,得到DE=BC,证明四边形BCDE为平行四边形,再根据得到BC=CD,从而证明菱形.
【详解】解:(1)连接BD,
∵,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)连接CD,
∵AD∥BC,
∴∠EDF=∠CBF,
∵,
∴BC=CD,
∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),
∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
【点睛】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF=DF.
20.
【分析】先根据平行线的性质得到,再根据等腰三角形的性质求出,即可利用三角形内角和定理求出的度数.
【详解】解:∵所对圆心角的度数为,
∴,
∵,
∴,
∵,
∴,
∴.
∴所对圆心角的度数为.
【点睛】本题主要考查了平行线的性质,圆的基本性质,等腰三角形的性质,三角形内角和定理,熟知相关知识是解题的关键.
21.(1)20°;(2)60°.
【分析】(1)由AB=BO,则∠AOB=∠1=∠A=20°;
(2)∠1=∠E,因此∠EOD=3∠A,即可求出∠EOD.
【详解】(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°
(2)解:
∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
【点睛】本题考查了圆的认识,等腰三角形的性质和三角形外角定理,解题的关键是能从图形中发现每个角之间的关系.
22.,理由见试题解析
【分析】由AB=AE,得出∠B=∠AEB,根据平行四边形的性质可得∠B=∠GAF,∠FAE=∠AEB,从而得到∠GAF=∠FAE,再由弧、弦的关系定理得出 .
【详解】,理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴.
23.见解析
【分析】根据题意圆的性质结合中心对称和轴对称的定义,设计轴对称图形或中心对称图形的图案即可.
【详解】(1)如图,是轴对称图形但不是中心对称图形;
(2)如图,是中心对称图形但不是轴对称图形;
(3)如图,既是轴对称图形又是中心对称图形.
【点睛】本题考查了圆的性质,轴对称图形和中心对称图形,掌握轴对称和中心对称图像的性质是解题的关键.
24.(1)证明见解析
(2)成立,证明见解析
【分析】(1)先利用HL定理判定Rt△OCM和Rt△ODN全等,再根据全等三角形的性质可得∶ ∠AOM=∠BON,最后根据同圆中,相等的圆心角所对的弧相等即可求证;
(2) 连接,根据已知条件,证明是等边三角形,所以∠MOC=∠NOD=∠MON,根据同圆中相等的圆心角所对弧相等即可求证.
【详解】(1)连接OM,ON,如图,
因为OM=ON,OA=OB,
∵AC=DB,
∴OC=OD,
在Rt△OCM和Rt△ODN中,
,
∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,
∴,
(2),理由如下,如图,连接,
∵C、D分别为OA、OB中点,
∴OC=OA=AC,OD=OB=DB,
MC⊥AB,ND⊥AB,
,
是等边三角形,
∴∠MOC=∠NOD=60°,
∴∠MON=60°,
∠MOC=∠NOD=∠MON
∴∠AOM=∠MON=∠BON,
.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等边三角形、全等三角形的判定与性质.
3.2圆的对称性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图, AB是⊙O的直径, CD是AO的垂直平分线, EF是OB的垂直平分线, 则下列结论正确的是 ( )
A.== B.
C. D.
2.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
3.如图,已知AD=BC,则AB与CD的关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
4.下列命题中,正确的是( )
A.垂直于弦的直径平分弦,并且平分弦所对的弧
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.AB,CD是⊙O的弦,若AB=CD,则AB∥CD
D.圆是轴对称图形,对称轴是圆的每一条直径
5.下列说法正确的是( )
A.长度相等的弧是等弧 B.半圆是弧
C.等弦对等圆心角 D.直径是最长的弦,半径是最短的弦
6.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.相等的圆心角所对的弦相等
C.相等的弧所对的弦相等 D.相等的弦所对的弧相等
7.如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为40°,70°,150°,则∠B的度数是( )
A.20° B.25° C.30° D.35°
8.如图,点A,B,C,D是⊙O上的四个点,且,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B. C. D.
9.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
A.AB=AD B.AC=BD C.BE=CD D.BE=AD
10.如图,为的弦,,则等于( )
A. B. C. D.
11.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
12.如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )
A.38° B.52° C.76° D.104°
二、填空题
13.已知扇形弧上连同两个端点共有4个点,将这4点与圆心连接,则共可得 个扇形.
14.已知⊙O的直径为cm,点A在⊙O上,则线段OA的长为 cm.
15.在中,已知, 那么线段与的大小关系是 .(从“<”或“=”或“>”中选择)
16.如图,点,点,点在上,分别连接,,.若,,则 .
17.如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么 , = ,∠AOC ∠BOD;
(2)如果AB=CD,那么 = , ;
(3)如果=,那么 , , .
三、解答题
18.如图,在中,,求证:
(1);
(2).
19.如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
20.如图,是的直径,点,在上,且点,在的异侧,连接,,.若所对圆心角的度数为70°,且,求所对圆心角的度数.
21.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数
(2)求∠EOD的度数
22.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断和是否相等,并说明理由.
23.利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)是中心对称图形但不是轴对称图形;
(3)既是轴对称图形又是中心对称图形.
24.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.
(1)求证:=;
(2)若C、D分别为OA、OB中点,则成立吗?
《3.2圆的对称性》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A B C A D B D
题号 11 12
答案 D C
1.A
【分析】如图,连接AD,OD,DF,OF,BF,根据垂直平分线的性质易证DF=DF=BF,再根据“在同圆或等圆中,所对的弦相等的两段弧是等弧”即可判断.
【详解】如图,连接AD,OD,DF,OF,BF,
∵CD是AO的垂直平分线, EF是OB的垂直平分线,
∴DF=CE=AB,AD=OD,OF=BF,
∴DF=DF=BF,
则==.
故选A.
【点睛】本题主要考查垂直平分线的性质,等弧的判定,解此题的关键在于熟练掌握其知识点.
2.C
【分析】利用垂径定理分别判断后即可确定正确的选项.
【详解】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
【点睛】本题考查了命题与定理的知识,解题的关键是理解垂径定理及其推理,难度不大.
3.B
【分析】由题知AD=BC,根据圆心角、弧、弦的关系,得出=.
再给=.两边加上,即可得到AB与CD的关系.
【详解】∵AD=BC,
∴=.
∴+=+,
即=.
∴AB=CD.
故选:B.
【点睛】本题考查了圆心角、弧、弦的关系定理,解题关键熟练掌握圆心角、弧、弦的关系定理;
4.A
【详解】试题分析:根据垂径定理即可判断A、B;根据AB和CD可能平行也可能相交,即可判断C;根据对称轴是直线,即可判断D.
解:A、垂直于弦的直径平分弦,且平分弦所对的弧,故本选项正确;
B、平分弦(弦不是直径)直径垂直于弦,并且平分弦所对的弧,故本选项错误;
C、AB和CD可能相交,故本选项错误;
D、圆是轴对称图形,对称轴是圆的每一条直径所在的直线,故本选项错误;
故选A.
点评:本题考查了垂径定理和圆的认识的应用,主要考查学生对定理的理解能力,题目比较典型,但是一道比较容易出错的题目.
5.B
【分析】根据连接圆上任意两点的线段叫弦,经过圆心的弦叫直径;圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆;在同圆或等圆中,等弦所对的弧对应相等,等弧所对的圆心角相等,逐项判断可得答案.
【详解】解:A.等弧指的是在同圆或等圆中,能够互相重合的弧,而不是长度相等,就一定能够重合,故此选项不符合题意;
B.半圆是弧,故此选项符合题意;
C.在同圆或等圆中,等弦所对的弧对应相等,等弧所对的圆心角相等,故此选项不符合题意;
D.直径是最长的弦,半径不是弦,故此选项不符合题意.
故选:B.
【点睛】本题考查圆的认识,在同圆或等圆中,弦,弧,圆心角的关系.解题的关键是掌握弧、半圆和弦的定义,弦、弧、圆心角的关系.
6.C
【分析】首先要明确是否同圆或者等圆,其次还要明确优弧还是劣弧.
【详解】A、B选项中的结论必须要有“同圆或等圆”的前提,故均错误;D选项除了要明确“同圆或等圆”外,还要明确是优弧还是劣弧,故也错误;
故选择C.
【点睛】对于定理,一定不能忽略它的前提和一些限制条件.
7.A
【分析】连结OD,如图,根据题意得∠DOC=30°,∠AOD=80°,由于OD=OA,则∠ADO=50°,然后利用三角形外角性质得∠ADO=∠B+∠DOB,得出∠B=50°-30°=20°即可.
【详解】解:连结OD,如图
则∠DOC=70°-40°=30°,∠AOD=150°-70°=80°,
∵OD=OA,
∴∠ADO=50°,
∵∠ADO=∠B+∠DOB,
∴∠B=50°-30°=20°.
故选A.
【点睛】本题考查圆周角定理、等腰三角形的性质、三角形的外角性质;由等腰三角形的性质得出∠ADO=50°是解题的关键.
8.D
【分析】在同圆中,根据圆心角、弧和弦之间的关系即可判断.
【详解】解:在⊙O中,
∵
∴,
故A、C选项正确,不符合题意;
∵,OA=OD,OB=OC
∴
∴
∵OE⊥AB,OF⊥CD,
∴
∴OE=OF
故B选项正确,不符合题意.
故选D
【点睛】本题考查圆的对称性,理解同圆中圆心角、弧和弦之间的关系是解题的关键.
9.B
【分析】连接BC,根据弧与弦的关系得出,进而判断即可.
【详解】连接BC,
∵
∴
∴
∴AC=BD
故选:B
【点睛】此题考查圆心角、弧、弦的关系,关键是根据弧与弦的关系得出.
10.D
【分析】先运用了等腰三角形的性质求出,再根据三角形的内角和是即可得.
【详解】解:,
为等腰三角形,
,
,
所以.
故选:D.
【点睛】本题考查了等腰三角形的性质,三角形的内角和定理,熟练运用等腰三角形的性质等边对等角是解题的关键.
11.D
【分析】对于A,直径是通过圆心且两个端点都在圆上的线段,即可进行判断;
对于B,能重合的弧叫等弧,即可进行判断;
对于C和D,分别根据等圆,直径,半圆的知识,也可进行判断.
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
【点睛】本题考查圆的认识,解题的关键是掌握弦,弧等知识,灵活运用所学知识解决问题
12.C
【分析】根据半径相等得到OM=ON,则∠M=∠N=52°,然后根据三角形内角和定理计算∠MON的度数.
【详解】∵OM=ON,
∴∠M=∠N=52°,
∴∠MON=180°-2×52°=76°.
故选C.
【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
13.6
【详解】如图,当扇形AOD的上有A、B、C、D四个点时,连接OA、OB、OC、OD,则图中的扇形有:扇形AOD、扇形AOC、扇形AOB、扇形BOD、扇形BOC、扇形COD,共计6个.
故答案为6.
14.
【详解】解:∵⊙O的直径为cm,
∴⊙O的半径为cm,
∵点A在⊙O上,
∴线段OA=cm.
故答案为.
15.
【分析】本题考查的是圆心角、弧、弦的关系、三角形三边关系,根据圆心角、弧、弦的关系定理和三角形三边关系定理解得即可.
【详解】解:∵
∴
∴
在中,
∴
16./20度
【分析】首先连接,,然后根据等弦对等圆心角得到,再根据三角形内角和得到,再由,,即可得到结果.
【详解】解:如图,连接,,
,
,,
,
,
,
,,
.
故答案为:.
【点睛】本题主要考查圆内相关概念和定理,三角形内角和定理等内容;掌握圆内相关概念是解题基础.
17.(1)AB=CD,, , = ;(2) , ,∠AOB=∠COD;(3)AB=CD,∠AOB=∠COD, =
【分析】根据在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等进行解答.
【详解】(1)∵∠AOB=∠COD,
∴AB=CD,,∠AOC=∠BOD;
(2)∵AB=CD,
∴,∠AOB=∠COD;
(3)∵,
∴AB=CD,∠AOB=∠COD,.
故答案为:(1)AB=CD,,,=;(2),,∠AOB=∠COD;(3)AB=CD,∠AOB=∠COD,=.
【点睛】本题考查了圆心角、弧、弦的关系,在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
18.(1)见解析
(2)见解析
【分析】本题考查了圆心角、弧、弦的关系,等腰三角形的性质,解答本题用到的知识点为:同弧所对的圆心角相等,等腰三角形两底角相等等.
(1)由,可知,得到;
(2)根据圆心角、弧、弦的关系由,得到,然后利用等腰三角形底角相等即可得到结论.
【详解】(1)证明:,
;
(2)证明:,
,
又,
,
即.
19.(1)见解析;(2)见解析
【分析】(1)连接BD,根据圆周角定理可得∠ADB=∠CBD,根据平行线的判定可得结论;
(2)证明△DEF≌△BCF,得到DE=BC,证明四边形BCDE为平行四边形,再根据得到BC=CD,从而证明菱形.
【详解】解:(1)连接BD,
∵,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)连接CD,
∵AD∥BC,
∴∠EDF=∠CBF,
∵,
∴BC=CD,
∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),
∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
【点睛】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF=DF.
20.
【分析】先根据平行线的性质得到,再根据等腰三角形的性质求出,即可利用三角形内角和定理求出的度数.
【详解】解:∵所对圆心角的度数为,
∴,
∵,
∴,
∵,
∴,
∴.
∴所对圆心角的度数为.
【点睛】本题主要考查了平行线的性质,圆的基本性质,等腰三角形的性质,三角形内角和定理,熟知相关知识是解题的关键.
21.(1)20°;(2)60°.
【分析】(1)由AB=BO,则∠AOB=∠1=∠A=20°;
(2)∠1=∠E,因此∠EOD=3∠A,即可求出∠EOD.
【详解】(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°
(2)解:
∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
【点睛】本题考查了圆的认识,等腰三角形的性质和三角形外角定理,解题的关键是能从图形中发现每个角之间的关系.
22.,理由见试题解析
【分析】由AB=AE,得出∠B=∠AEB,根据平行四边形的性质可得∠B=∠GAF,∠FAE=∠AEB,从而得到∠GAF=∠FAE,再由弧、弦的关系定理得出 .
【详解】,理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴.
23.见解析
【分析】根据题意圆的性质结合中心对称和轴对称的定义,设计轴对称图形或中心对称图形的图案即可.
【详解】(1)如图,是轴对称图形但不是中心对称图形;
(2)如图,是中心对称图形但不是轴对称图形;
(3)如图,既是轴对称图形又是中心对称图形.
【点睛】本题考查了圆的性质,轴对称图形和中心对称图形,掌握轴对称和中心对称图像的性质是解题的关键.
24.(1)证明见解析
(2)成立,证明见解析
【分析】(1)先利用HL定理判定Rt△OCM和Rt△ODN全等,再根据全等三角形的性质可得∶ ∠AOM=∠BON,最后根据同圆中,相等的圆心角所对的弧相等即可求证;
(2) 连接,根据已知条件,证明是等边三角形,所以∠MOC=∠NOD=∠MON,根据同圆中相等的圆心角所对弧相等即可求证.
【详解】(1)连接OM,ON,如图,
因为OM=ON,OA=OB,
∵AC=DB,
∴OC=OD,
在Rt△OCM和Rt△ODN中,
,
∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,
∴,
(2),理由如下,如图,连接,
∵C、D分别为OA、OB中点,
∴OC=OA=AC,OD=OB=DB,
MC⊥AB,ND⊥AB,
,
是等边三角形,
∴∠MOC=∠NOD=60°,
∴∠MON=60°,
∠MOC=∠NOD=∠MON
∴∠AOM=∠MON=∠BON,
.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等边三角形、全等三角形的判定与性质.
