第一章直角三角形的边角关系 单元练习 北师大版数学九年级下册(含解析)
文档属性
| 名称 | 第一章直角三角形的边角关系 单元练习 北师大版数学九年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 06:19:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章直角三角形的边角关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠C=90°,tanA=,△ABC的周长为60,那么△ABC的面积为( )
A.60 B.30 C.240 D.120
2.如果sin2α+cos230°=1,那么锐角α的度数是( )
A.15° B.30° C.45° D.60°
3.利用数学课本上的计算器计算,正确的按键顺序是( )
A. B.
C. D.
4.如果把∠C为直角的各边的长都扩大到原来的2倍,那么锐角A的各三角比的值( )
A.都扩大到原来的2倍 B.都缩小到原来的一半
C.都没有变化 D.有些有变化
5.在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的各个三角函数值 ( )
A.缩小 B.扩大3倍 C.不变 D.缩小3倍
6.如图,在边长为的方格纸中,与交于点,其中、均为所在正方形小方格一边的中点,则( )
A. B. C. D.
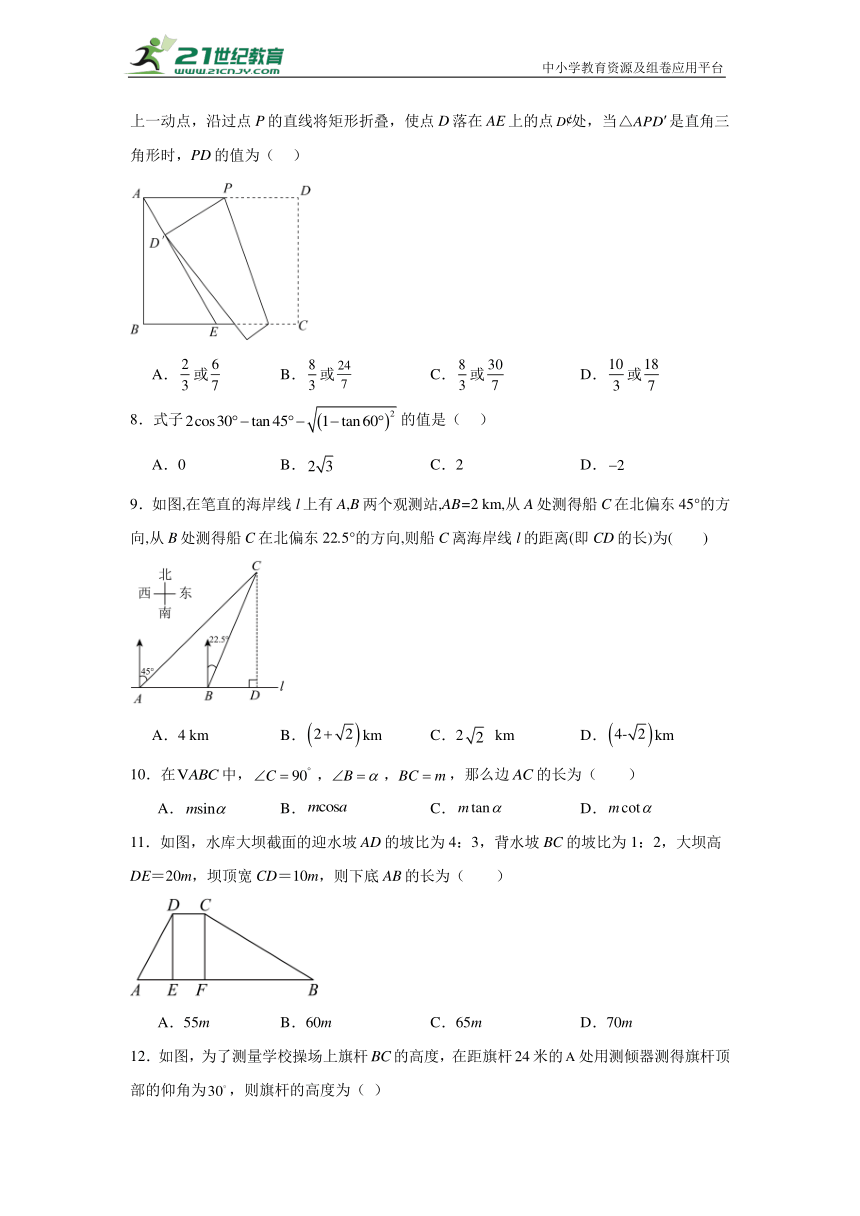
7.如图,在矩形ABCD中,BC=6,E是BC的中点,连接AE,,P是AD边上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点处,当是直角三角形时,PD的值为( )
A.或 B.或 C.或 D.或
8.式子的值是( )
A.0 B. C.2 D.
9.如图,在笔直的海岸线l上有A,B两个观测站,AB=2 km,从A处测得船C在北偏东45°的方向,从B处测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4 km B.km C.2 km D.km
10.在中,,那么边的长为( )
A. B. C. D.
11.如图,水库大坝截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( )
A.55m B.60m C.65m D.70m
12.如图,为了测量学校操场上旗杆的高度,在距旗杆米的处用测倾器测得旗杆顶部的仰角为,则旗杆的高度为( )
A.米 B.米 C.米 D.米
二、填空题
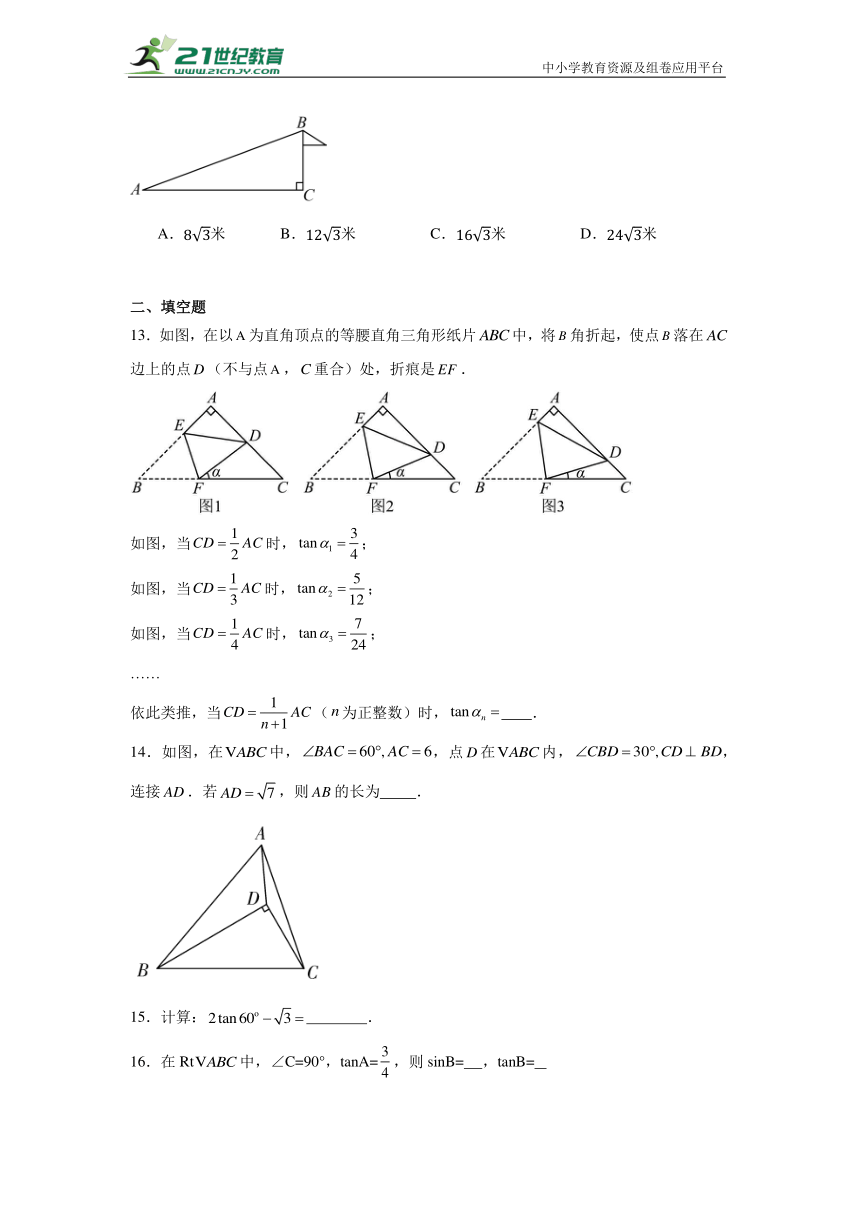
13.如图,在以为直角顶点的等腰直角三角形纸片中,将角折起,使点落在边上的点(不与点,重合)处,折痕是.
如图,当时,;
如图,当时,;
如图,当时,;
……
依此类推,当(为正整数)时, .
14.如图,在中,,点在内,,连接.若,则的长为 .
15.计算: .
16.在Rt中,∠C=90°,tanA=,则sinB= ,tanB=
17.计算: .
三、解答题
18.如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛上的观测点进行观测,从A岛测得渔船在南偏东方向C处,B岛在南偏东方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?
(参考数据:)
19.如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号).
20.为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡长米,坡角(即)为,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡(下面两个小题结果都保留根号).
(1)若修建的斜坡的坡比为,求休闲平台的长是多少米?
(2)一座建筑物距离A点33米远(即米),小亮在D点测得建筑物顶部H的仰角(即)为.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且,问建筑物高为多少米?
21.如图,在水平地面上有一幢房屋与一棵树,在地面观测点处测得屋顶与树梢的仰角分别是与,,在屋顶处测得.若房屋的高米.求树高的长度.
22.如图,小明想测量电线杆的高度,发现电线杆的影子恰好落在土坡的坡面和地面上,量得与地平面成角,且此时测得长的标杆在地面的影子长为,则电线杆的高度为多少(结果精确到)?
23.(1)通过用计算器计算,比较下列各对数的大小,并提出你的猜想:
①_______;
②_______;
③_______;
④_______;
⑤_______.
猜想:已知,则_______;
(2)如图,在中,,请根据提示,利用面积方法验证结论.
24.某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成角,房屋向南的窗户AB高.现要在窗户外面的上方安装一个水平遮阳篷(如图所示).要使太阳光线不能直接射入室内,遮阳篷AC的宽度至少为多少?
《第一章直角三角形的边角关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C C B B A B C
题号 11 12
答案 C A
1.D
【分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.
【详解】如图所示,
由tanA=,
设BC=12x,AC=5x,根据勾股定理得:AB=13x,
由题意得:12x+5x+13x=60,
解得:x=2,
∴BC=24,AC=10,
则△ABC面积为120,
故选D.
【点睛】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.
2.B
【详解】解法一:由同角三角函数关系,sin2a+cos2a=1,所以a=30°,选B.
解法二:sin2a+cos230°=1, cos30°= sin2a=1- cos230°=1-,sina=,
sina= , a=30°,选B.
点睛:(1)掌握同角三角函数的关系sin2a+cos2a=1,可以为解题带来方便.
(2)熟练记忆特殊三角函数值对应的角度.
3.B
【分析】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.根据计算器的使用方法,可得答案.
【详解】用计算器计算,按键顺序是
故选B
4.C
【分析】根据正弦、余弦、正切的定义即可得.
【详解】在中,,
,
,
则当各边的长都扩大到原来的2倍,锐角A的各三角比的值都没有变化,
故选:C.
【点睛】本题考查了正弦、余弦、正切的定义,熟记定义是解题关键.
5.C
【分析】锐角三角函数的概念:在直角三角形中,锐角A的正切值为对边和邻边的比值,正弦是对边a与斜边c的比,余弦是邻边b与斜边c的比.一个角的锐角三角函数值只和角的大小有关,与角的边的长短无关.
【详解】由题意可知:如果各边长度都扩大3倍,所得三角形与原三角形相似,三个角的大小不变,那么锐角A的各个三角函数值不变.
故选C.
【点睛】此题主要考查了锐角三角函数的概念,正确理解锐角三角函数的概念是解决问题的关键.
6.B
【分析】过点作于点,根据题意得出,根据正切的定义即可求解.
【详解】解:如图所示,过点作于点,
依题意,,
∴,
故选:B.
【点睛】本题考查了求正切,熟练掌握正切的定义是解题的关键.
7.B
【分析】根据矩形的性质得到AB=CD,AD=BC,∠B=90°,根据勾股定理求得AE,当△APD'是直角三角形时,分两种情况①当∠AD'P=90°时②当∠APD'=90°时分类计算即可;
【详解】∵四边形ABCD是矩形,
∴AB=CD,∠B=90°,
∵BC=6,E是BC的中点,
∴BE=3,
∵,
∴,
∴CD=4,
在Rt△ABE中,AE,
∵四边形ABCD是矩形,
,
由折叠可知,PD=PD',
设PD=x,则PD'=x,AP=6﹣x,
当△APD'是直角三角形时,
①当∠AD'P=90°时,
∴∠AD'P=∠B=90°,
∵AD∥BC,
∴∠PAD'=∠AEB,
∴△ABE∽△PD'A,
∴,
∴,
∴x,
∴PD;
②当∠APD'=90°时,
∴∠APD'=∠B=90°,
∵∠PAE=∠AEB,
∴△APD'∽△EBA,
∴,
∴,
∴x,
∴PD;
综上所述:当△APD'是直角三角形时,PD的值为或;
故选:B.
【点睛】本题主要考查了矩形的性质,勾股定理,直角三角形的性质,相似三角形的判定与性质,牢固掌握以上知识点并准确计算是解题的关键.
8.A
【分析】根据特殊角的三角函数值计算即可.
【详解】解:原式
=0
故选:A.
【点睛】本题考查特殊角的三角函数值及二次根式的混合运算,解题关键是熟练掌握特殊角的三角函数值.
9.B
【详解】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可知BD=BE=km,因此CD=AD=AB+BD=(2+)km.
故选B
考点:解直角三角形的应用
10.C
【分析】由题意可知,将代入即可求得.
【详解】如图所示:在中,,
,
,
故选:C.
【点睛】本题考查了解直角三角形,锐角三角函数的定义,明确锐角三角函数的定义求得是解题的关键.
11.C
【分析】本题根据迎水坡坡比以及DE长度求解AE,根据背水坡坡比以及CF长度求解BF,最后将AE、EF、BF长度相加即可求得AB.
【详解】解:由题已知:四边形CDEF为矩形,
∵DE=20m,DE:AE=4:3,
∴AE=15m,
∵CF=DE=20m,CF:BF=1:2,
∴BF=40m,
又∵EF=CD=10m,
∴AB=AE+EF+BF=15+10+40=65m.
故选:C.
【点睛】本题考查解直角三角形的应用,即坡度坡角问题,解题关键是确定坡度比的比例关系,其次注意计算要仔细.
12.A
【分析】根据锐角三角函数关系得出tan30°=进而求出BC的长,即可得出答案.
【详解】根据题意得出:AC=24m,∠A=30°,
则tan30°==,
解得:BC=8.
故选A.
【点睛】考查了解直角三角中仰角问题,根据已知得出AC=24m,∠A=30°再利用锐角三角函数求出是解题关键.
13.
【分析】根据题意得到正切值的分子的规律和勾股数的规律,再进行计算即可得到答案.
【详解】观察可知,正切值的分子是3,5,7,9,…,,
分母与勾股数有关系,分别是勾股数3,4,5;5,12,13;7,24,25;9,40,41;…,,,中的中间一个.
∴.
故答案为.
【点睛】本题考查规律,解题的关键是由题意得到规律.
14.8或10
【详解】【思维构建】易得,由已知考虑以为顶点构造手拉手相似,即作
解法一:如图,过点作,,连接交于点,过点作于点,
则是等边三角形,
.
,
,
,
,
.
.
设,则,
在中,由勾股定理得,
解得或.
解法二:如图,在的延长线上作,则,
得是等边三角形,过点作于点,
连接,过点作于点,易得,得,
得,从而设,则,
得,在中,由勾股定理得,
解得或,则或,进而得或.
15.
【分析】根据特殊角的三角函数值即可求解.
【详解】原式=2-=
【点睛】此题主要考查特殊角的三角函数值,解题的关键是熟知特殊角的三角函数值.
16.
【详解】试题分析:由∠C=90°,tanA=可得,即可求得结果.
∵∠C=90°,tanA=
∴
∴,
考点:三角函数
点评:计算能力是学生必须具备的基本能力,中考中各种题型中均会涉及到计算问题,因而学生应该努力提升自己的计算能力.
17./
【分析】根据特殊角的三角函数值,化简绝对值,进行计算即可求解.
【详解】解:
.
故答案为:.
【点睛】本题考查了实数的混合运算,牢记特殊角的三角函数值是解题的关键.
18.调度中心应该派遣B岛上的维修船.
【分析】本题考查了解直角三角形的应用 方向角问题,难度适中,通过作辅助线,构造直角三角形,进而解直角三角形求出与的值是解题的关键.作的延长线于点D,先解,求出,再解,求出,则.然后分别求出A岛、B岛上维修船需要的时间,则派遣用时较少的岛上的维修船.
【详解】解:如图,作的延长线于点D,
在中,
(海里),
(海里).
在中,(海里),
(海里).
∴(海里).
∴A岛上维修船需要时间(小时),
B岛上维修船需要时间(小时).
∵,
∴调度中心应该派遣B岛上的维修船.
19.2米
【分析】在Rt△ACF中,根据三角函数的定义得到AF=AC tan60°=7米,在Rt△ABE中,根据三角函数的定义得到AE=AB tan30°=15×=5米,进而得到结论.
【详解】解:在Rt△ACF中,∵∠ACF=60°,AC=7米,
∴AF=AC tan60°=7米,
∵BC=8米,
∴AB=15米,
在Rt△ABE中,∵∠B=30°,
∴AE=AB tan30°=15×=5米,
∴EF=AF﹣AE=7﹣5=2(米),
答:信号塔EF的高度为2米.
【点睛】本题考查了解直角三角形仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形;难点是找到并运用题中相等的线段.
20.(1)休闲平台的长是米
(2)建筑物的高为米
【分析】本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题,解决本题的关键是熟练应用坡度和坡角.
(1)根据得,由为中点得,进而可求,,再根据斜坡的坡比为即可求得的长;
(2)可以设,则可得,再根据特殊角三角函数即可求得的高.
【详解】(1)解:根据题意可知:,
∴,
∵为中点,
∴,
∴,
∴,
∵斜坡的坡比为,
∴,
解得,
∴米;
(2)由(1)可得,
则,
设米,则米,
米,
在中,即,
解得:,
答:建筑物别的高为米.
21.树的高为米.
【详解】试题分析:首先解直角三角形求得表示出AC,AD的长,进而利用直角三角函数,求出答案.
试题解析:如图3,在中,,,
∴ ;
在中,,
∴ ;
在中,,
答:树的高为米.
22.
【详解】解:延长交的延长线于点,过点作于点.在中,由,得,.长的标杆在地面的影子长为,,得..,,即电线杆的高度约为.
【易错点分析】误认为的影长是地面影长加上坡面影长,因为长的标杆在地面的影子长为,所以的影长也应该是地面上的影长,即斜坡的影长也要转化到地面上来.是的影长,要根据物高与影长成比例计算,在中要根据边角关系计算,两者之间没有联系,易错误地认为.
23.(1)①=;②=;③=;④=;⑤=;猜想:=;(2)见解析
【分析】(1)根据计算器计算即可得出结论;
(2)根据三角函数定义可得,由,可求;再根据锐角三角函数定义可得,可求,可求,比较即可得出结论.
【详解】(1)①=;
②=;
③=;
④=;
⑤=.
猜想:已知,则=;
(2)证明:图1中,
∵,
∴,
又∵,
∴;
图2中,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】本题考查计算器求值比大小,锐角三角函数定义,从三角形面积不同算法,得出是解题关键.
24.遮阳篷AC的宽度至少为.
【分析】利用相应的三角函数可求得此时AC的长度,当遮阳蓬的宽度大于AC的宽度时,太阳光线照在点B的下方,也不能射入室内.
【详解】解:此时△ABC为∠ABC是30°的直角三角形,
则AC=AB×tan30°= AB=,
当遮阳蓬AC的宽度大于时,太阳光线不能射入室内,
故答案为.
【点睛】考查了解直角三角形的应用和平行投影.用到的知识点为:遮阳板越小,透进屋内的阳光越多,反正越少;关键是求得此时遮阳板的长度.
第一章直角三角形的边角关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠C=90°,tanA=,△ABC的周长为60,那么△ABC的面积为( )
A.60 B.30 C.240 D.120
2.如果sin2α+cos230°=1,那么锐角α的度数是( )
A.15° B.30° C.45° D.60°
3.利用数学课本上的计算器计算,正确的按键顺序是( )
A. B.
C. D.
4.如果把∠C为直角的各边的长都扩大到原来的2倍,那么锐角A的各三角比的值( )
A.都扩大到原来的2倍 B.都缩小到原来的一半
C.都没有变化 D.有些有变化
5.在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的各个三角函数值 ( )
A.缩小 B.扩大3倍 C.不变 D.缩小3倍
6.如图,在边长为的方格纸中,与交于点,其中、均为所在正方形小方格一边的中点,则( )
A. B. C. D.
7.如图,在矩形ABCD中,BC=6,E是BC的中点,连接AE,,P是AD边上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点处,当是直角三角形时,PD的值为( )
A.或 B.或 C.或 D.或
8.式子的值是( )
A.0 B. C.2 D.
9.如图,在笔直的海岸线l上有A,B两个观测站,AB=2 km,从A处测得船C在北偏东45°的方向,从B处测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4 km B.km C.2 km D.km
10.在中,,那么边的长为( )
A. B. C. D.
11.如图,水库大坝截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( )
A.55m B.60m C.65m D.70m
12.如图,为了测量学校操场上旗杆的高度,在距旗杆米的处用测倾器测得旗杆顶部的仰角为,则旗杆的高度为( )
A.米 B.米 C.米 D.米
二、填空题
13.如图,在以为直角顶点的等腰直角三角形纸片中,将角折起,使点落在边上的点(不与点,重合)处,折痕是.
如图,当时,;
如图,当时,;
如图,当时,;
……
依此类推,当(为正整数)时, .
14.如图,在中,,点在内,,连接.若,则的长为 .
15.计算: .
16.在Rt中,∠C=90°,tanA=,则sinB= ,tanB=
17.计算: .
三、解答题
18.如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛上的观测点进行观测,从A岛测得渔船在南偏东方向C处,B岛在南偏东方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?
(参考数据:)
19.如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号).
20.为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡长米,坡角(即)为,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡(下面两个小题结果都保留根号).
(1)若修建的斜坡的坡比为,求休闲平台的长是多少米?
(2)一座建筑物距离A点33米远(即米),小亮在D点测得建筑物顶部H的仰角(即)为.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且,问建筑物高为多少米?
21.如图,在水平地面上有一幢房屋与一棵树,在地面观测点处测得屋顶与树梢的仰角分别是与,,在屋顶处测得.若房屋的高米.求树高的长度.
22.如图,小明想测量电线杆的高度,发现电线杆的影子恰好落在土坡的坡面和地面上,量得与地平面成角,且此时测得长的标杆在地面的影子长为,则电线杆的高度为多少(结果精确到)?
23.(1)通过用计算器计算,比较下列各对数的大小,并提出你的猜想:
①_______;
②_______;
③_______;
④_______;
⑤_______.
猜想:已知,则_______;
(2)如图,在中,,请根据提示,利用面积方法验证结论.
24.某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成角,房屋向南的窗户AB高.现要在窗户外面的上方安装一个水平遮阳篷(如图所示).要使太阳光线不能直接射入室内,遮阳篷AC的宽度至少为多少?
《第一章直角三角形的边角关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B C C B B A B C
题号 11 12
答案 C A
1.D
【分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.
【详解】如图所示,
由tanA=,
设BC=12x,AC=5x,根据勾股定理得:AB=13x,
由题意得:12x+5x+13x=60,
解得:x=2,
∴BC=24,AC=10,
则△ABC面积为120,
故选D.
【点睛】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.
2.B
【详解】解法一:由同角三角函数关系,sin2a+cos2a=1,所以a=30°,选B.
解法二:sin2a+cos230°=1, cos30°= sin2a=1- cos230°=1-,sina=,
sina= , a=30°,选B.
点睛:(1)掌握同角三角函数的关系sin2a+cos2a=1,可以为解题带来方便.
(2)熟练记忆特殊三角函数值对应的角度.
3.B
【分析】本题主要考查了计算器-三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.根据计算器的使用方法,可得答案.
【详解】用计算器计算,按键顺序是
故选B
4.C
【分析】根据正弦、余弦、正切的定义即可得.
【详解】在中,,
,
,
则当各边的长都扩大到原来的2倍,锐角A的各三角比的值都没有变化,
故选:C.
【点睛】本题考查了正弦、余弦、正切的定义,熟记定义是解题关键.
5.C
【分析】锐角三角函数的概念:在直角三角形中,锐角A的正切值为对边和邻边的比值,正弦是对边a与斜边c的比,余弦是邻边b与斜边c的比.一个角的锐角三角函数值只和角的大小有关,与角的边的长短无关.
【详解】由题意可知:如果各边长度都扩大3倍,所得三角形与原三角形相似,三个角的大小不变,那么锐角A的各个三角函数值不变.
故选C.
【点睛】此题主要考查了锐角三角函数的概念,正确理解锐角三角函数的概念是解决问题的关键.
6.B
【分析】过点作于点,根据题意得出,根据正切的定义即可求解.
【详解】解:如图所示,过点作于点,
依题意,,
∴,
故选:B.
【点睛】本题考查了求正切,熟练掌握正切的定义是解题的关键.
7.B
【分析】根据矩形的性质得到AB=CD,AD=BC,∠B=90°,根据勾股定理求得AE,当△APD'是直角三角形时,分两种情况①当∠AD'P=90°时②当∠APD'=90°时分类计算即可;
【详解】∵四边形ABCD是矩形,
∴AB=CD,∠B=90°,
∵BC=6,E是BC的中点,
∴BE=3,
∵,
∴,
∴CD=4,
在Rt△ABE中,AE,
∵四边形ABCD是矩形,
,
由折叠可知,PD=PD',
设PD=x,则PD'=x,AP=6﹣x,
当△APD'是直角三角形时,
①当∠AD'P=90°时,
∴∠AD'P=∠B=90°,
∵AD∥BC,
∴∠PAD'=∠AEB,
∴△ABE∽△PD'A,
∴,
∴,
∴x,
∴PD;
②当∠APD'=90°时,
∴∠APD'=∠B=90°,
∵∠PAE=∠AEB,
∴△APD'∽△EBA,
∴,
∴,
∴x,
∴PD;
综上所述:当△APD'是直角三角形时,PD的值为或;
故选:B.
【点睛】本题主要考查了矩形的性质,勾股定理,直角三角形的性质,相似三角形的判定与性质,牢固掌握以上知识点并准确计算是解题的关键.
8.A
【分析】根据特殊角的三角函数值计算即可.
【详解】解:原式
=0
故选:A.
【点睛】本题考查特殊角的三角函数值及二次根式的混合运算,解题关键是熟练掌握特殊角的三角函数值.
9.B
【详解】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可知BD=BE=km,因此CD=AD=AB+BD=(2+)km.
故选B
考点:解直角三角形的应用
10.C
【分析】由题意可知,将代入即可求得.
【详解】如图所示:在中,,
,
,
故选:C.
【点睛】本题考查了解直角三角形,锐角三角函数的定义,明确锐角三角函数的定义求得是解题的关键.
11.C
【分析】本题根据迎水坡坡比以及DE长度求解AE,根据背水坡坡比以及CF长度求解BF,最后将AE、EF、BF长度相加即可求得AB.
【详解】解:由题已知:四边形CDEF为矩形,
∵DE=20m,DE:AE=4:3,
∴AE=15m,
∵CF=DE=20m,CF:BF=1:2,
∴BF=40m,
又∵EF=CD=10m,
∴AB=AE+EF+BF=15+10+40=65m.
故选:C.
【点睛】本题考查解直角三角形的应用,即坡度坡角问题,解题关键是确定坡度比的比例关系,其次注意计算要仔细.
12.A
【分析】根据锐角三角函数关系得出tan30°=进而求出BC的长,即可得出答案.
【详解】根据题意得出:AC=24m,∠A=30°,
则tan30°==,
解得:BC=8.
故选A.
【点睛】考查了解直角三角中仰角问题,根据已知得出AC=24m,∠A=30°再利用锐角三角函数求出是解题关键.
13.
【分析】根据题意得到正切值的分子的规律和勾股数的规律,再进行计算即可得到答案.
【详解】观察可知,正切值的分子是3,5,7,9,…,,
分母与勾股数有关系,分别是勾股数3,4,5;5,12,13;7,24,25;9,40,41;…,,,中的中间一个.
∴.
故答案为.
【点睛】本题考查规律,解题的关键是由题意得到规律.
14.8或10
【详解】【思维构建】易得,由已知考虑以为顶点构造手拉手相似,即作
解法一:如图,过点作,,连接交于点,过点作于点,
则是等边三角形,
.
,
,
,
,
.
.
设,则,
在中,由勾股定理得,
解得或.
解法二:如图,在的延长线上作,则,
得是等边三角形,过点作于点,
连接,过点作于点,易得,得,
得,从而设,则,
得,在中,由勾股定理得,
解得或,则或,进而得或.
15.
【分析】根据特殊角的三角函数值即可求解.
【详解】原式=2-=
【点睛】此题主要考查特殊角的三角函数值,解题的关键是熟知特殊角的三角函数值.
16.
【详解】试题分析:由∠C=90°,tanA=可得,即可求得结果.
∵∠C=90°,tanA=
∴
∴,
考点:三角函数
点评:计算能力是学生必须具备的基本能力,中考中各种题型中均会涉及到计算问题,因而学生应该努力提升自己的计算能力.
17./
【分析】根据特殊角的三角函数值,化简绝对值,进行计算即可求解.
【详解】解:
.
故答案为:.
【点睛】本题考查了实数的混合运算,牢记特殊角的三角函数值是解题的关键.
18.调度中心应该派遣B岛上的维修船.
【分析】本题考查了解直角三角形的应用 方向角问题,难度适中,通过作辅助线,构造直角三角形,进而解直角三角形求出与的值是解题的关键.作的延长线于点D,先解,求出,再解,求出,则.然后分别求出A岛、B岛上维修船需要的时间,则派遣用时较少的岛上的维修船.
【详解】解:如图,作的延长线于点D,
在中,
(海里),
(海里).
在中,(海里),
(海里).
∴(海里).
∴A岛上维修船需要时间(小时),
B岛上维修船需要时间(小时).
∵,
∴调度中心应该派遣B岛上的维修船.
19.2米
【分析】在Rt△ACF中,根据三角函数的定义得到AF=AC tan60°=7米,在Rt△ABE中,根据三角函数的定义得到AE=AB tan30°=15×=5米,进而得到结论.
【详解】解:在Rt△ACF中,∵∠ACF=60°,AC=7米,
∴AF=AC tan60°=7米,
∵BC=8米,
∴AB=15米,
在Rt△ABE中,∵∠B=30°,
∴AE=AB tan30°=15×=5米,
∴EF=AF﹣AE=7﹣5=2(米),
答:信号塔EF的高度为2米.
【点睛】本题考查了解直角三角形仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形;难点是找到并运用题中相等的线段.
20.(1)休闲平台的长是米
(2)建筑物的高为米
【分析】本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题,解决本题的关键是熟练应用坡度和坡角.
(1)根据得,由为中点得,进而可求,,再根据斜坡的坡比为即可求得的长;
(2)可以设,则可得,再根据特殊角三角函数即可求得的高.
【详解】(1)解:根据题意可知:,
∴,
∵为中点,
∴,
∴,
∴,
∵斜坡的坡比为,
∴,
解得,
∴米;
(2)由(1)可得,
则,
设米,则米,
米,
在中,即,
解得:,
答:建筑物别的高为米.
21.树的高为米.
【详解】试题分析:首先解直角三角形求得表示出AC,AD的长,进而利用直角三角函数,求出答案.
试题解析:如图3,在中,,,
∴ ;
在中,,
∴ ;
在中,,
答:树的高为米.
22.
【详解】解:延长交的延长线于点,过点作于点.在中,由,得,.长的标杆在地面的影子长为,,得..,,即电线杆的高度约为.
【易错点分析】误认为的影长是地面影长加上坡面影长,因为长的标杆在地面的影子长为,所以的影长也应该是地面上的影长,即斜坡的影长也要转化到地面上来.是的影长,要根据物高与影长成比例计算,在中要根据边角关系计算,两者之间没有联系,易错误地认为.
23.(1)①=;②=;③=;④=;⑤=;猜想:=;(2)见解析
【分析】(1)根据计算器计算即可得出结论;
(2)根据三角函数定义可得,由,可求;再根据锐角三角函数定义可得,可求,可求,比较即可得出结论.
【详解】(1)①=;
②=;
③=;
④=;
⑤=.
猜想:已知,则=;
(2)证明:图1中,
∵,
∴,
又∵,
∴;
图2中,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】本题考查计算器求值比大小,锐角三角函数定义,从三角形面积不同算法,得出是解题关键.
24.遮阳篷AC的宽度至少为.
【分析】利用相应的三角函数可求得此时AC的长度,当遮阳蓬的宽度大于AC的宽度时,太阳光线照在点B的下方,也不能射入室内.
【详解】解:此时△ABC为∠ABC是30°的直角三角形,
则AC=AB×tan30°= AB=,
当遮阳蓬AC的宽度大于时,太阳光线不能射入室内,
故答案为.
【点睛】考查了解直角三角形的应用和平行投影.用到的知识点为:遮阳板越小,透进屋内的阳光越多,反正越少;关键是求得此时遮阳板的长度.
