北师大版数学七年级上册第六章第3节数据的表示课时练习
文档属性
| 名称 | 北师大版数学七年级上册第六章第3节数据的表示课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-13 14:31:06 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
北师大版数学七年级上册第6章第3节数据的表示同步检测
一、选择题
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数
B.等于数据总数
C.大于数据总数
D.不能确定
答案:B
解析:解答:由于各小组的频数之和等于数据总数,所以选项B正确.
故选:B.
分析:根据在频数分布表的绘制方法,各小组的频数之和等于数据的总数进行选择.
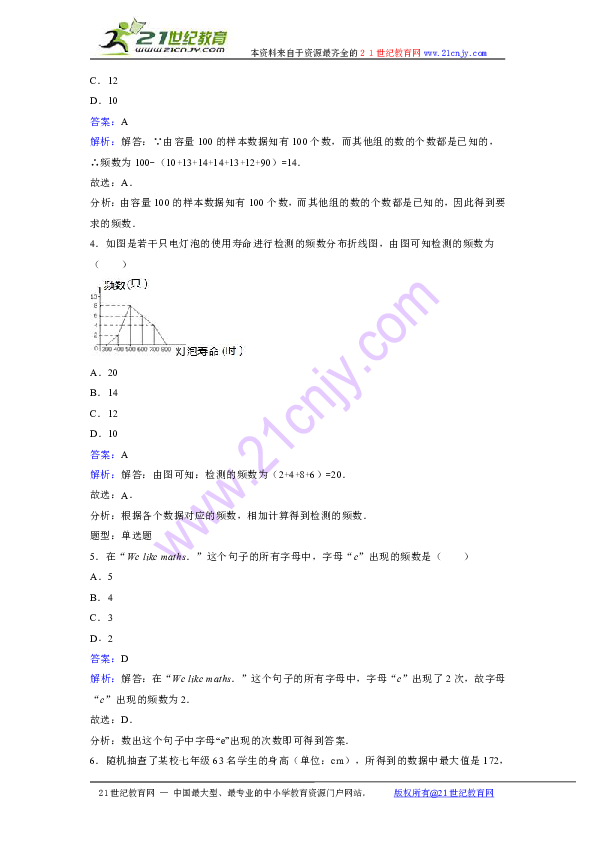
2.调查某小区内30户居民月人均收入情况,制成如下的频数分布直方图,收入在1200~1240元的频数是( )
A.12
B.13
C.14
D.15
答案:C
解析:解答:根据题意可知:共30户接受调查,其中1200以下的有3+7=10户,1400以上的有4+1+1=6户;那么收入在1200~1240元的频数是30-6-10=14.
故选:C.
分析:从图中得出1200以下和1400以上的频数,则收入在1200~1240元的频数=30-1200以下的频数-1400以上的频数.
3.容量100的样本数据,按从小到大的顺序分8组,如表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
第三组的频数是( )
A.14
B.13
C.12
D.10
答案:A
解析:解答:∵由容量100的样本数据知有100个数,而其他组的数的个数都是已知的,
∴频数为100-(10+13+14+14+13+12+90)=14.
故选:A.
分析:由容量100的样本数据知有100个数,而其他组的数的个数都是已知的,因此得到要求的频数.
4.如图是若干只电灯泡的使用寿命进行检测的频数分布折线图,由图可知检测的频数为( )
A.20
B.14
C.12
D.10
答案:A
解析:解答:由图可知:检测的频数为(2+4+8+6)=20.
故选:A.
分析:根据各个数据对应的频数,相加计算得到检测的频数.
题型:单选题
5.在“We like maths.”这个句子的所有字母中,字母“e”出现的频数是( )
A.5
B.4
C.3
D.2
答案:D
解析:解答:在“We like maths.”这个句子的所有字母中,字母“e”出现了2次,故字母“e”出现的频数为2.
故选:D.
分析:数出这个句子中字母“e”出现的次数即可得到答案.
6.随机抽查了某校七年级63名学生的身高(单位:cm),所得到的数据中最大值是172,最小值是149、若取组距为4,则这些数据可分成( )组.
A.5
B.6
C.7
D.8
答案:B
解析:解答:(172-149)÷4=23÷4≈6组.
故选:B.
分析:计算最大值与最小值的差,除以组距进行求得.
7.抛硬币15次,有6次出现正面,9次出现反面,则出现正面的频数是( )
A.6
B.9
C.15
D.3
答案:A
解析:解答:抛硬币15次,有6次出现正面,9次出现反面,则出现正面的频数是6.
故选:A.
分析:根据频数的概念进行选择,频数是表示一组数据中,符合条件的对象出现的次数.
8.以下表格是某校初一(1)班班长候选人得票数领先的三位同学的得票情况,则小明得票的频数是( )
候选人 小红 小明 小丽
唱票记录 正正正一 正 正正正正正一
A.16
B.5
C.21
D.42
答案:B
解析:解答:根据小明得到唱票记录可得小明得票的频数是5.
故选:B.
分析:此题须根据小明得到唱票记录得出小明得票的频数.
9.一个射手连续射靶10次,其中1次射中10环,6次射中9环,3次射中8环,则射中( )环的频数最大.
A.6
B.8
C.9
D.10
答案:C
解析:解答:根据题意,可知6次射中9环,次数最多;所以射中9环的频数最大.
故选:C.
分析:根据各个频数,进行比较得出最大值.
10.一年中,31号出现的频数是( )
A.7
B.6
C.5
D.12
答案:A
解析:解答:一年中,有7个月有31天,所以一年中,31出现的频数是7.
故选:A.
分析:根据频数的概念,结合一年中,有几个月是31天可以得到答案.
11.大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90-110这一组的频数是( )
A.2
B.4
C.6
D.14
答案:B
解析:解答:跳绳次数在90~110之间的数据有91,93,100,102四个,所以频数为4.
故选:B.
分析:根据频数的定义,从数据中数出在90~110这一组的数据个数即可得到答案.
12.一组数据的最小数是12,最大数是38,如果分组的组距相等,且组距为3,则分组后的第一组为( )
A.11.5~13.5
B.11.5~14.5
C.12.5~14.5
D.12.5~15.5
答案:B
解析:因为这组数据的最小数是12,所以第一组应从11.5开始,因为12.5>12,故排除C、D;又组距为3,所以分组后的第一组为11.5~14.5.
故选:B.
分析:先由这组数据的最小数是12,排除C、D,再根据组距为3,进一步得出答案.
13.下列说法正确的是( )
A.样本的数据个数等于频数之和
B.扇形统计图可以告诉我们各部分的数量分别是多少
C.如果一组数据可以用扇形统计图表示,那么它一定可以用频数分布直方图表示
D.将频数分布直方图中小长方形上面一边的一个端点顺次连接起来,就可以得到频数折线图
答案:A
解析:解答:样本的数据个数相当于样本容量,频数之和等于样本容量,所以选项A正确;
扇形统计图只可以得到各部分数据的比例,不能得到各部分的数量,所以选项B错误;
作扇形统计图只要知道各部分的比例就行,频数分布直方图必须知道各部分的数量,所以选项C错误;
将直方图上方边的中点顺序连接起来可以得到频数折线图,所以选项D错误.
故选:A.
分析:根据频数、频数分布直方图、频数折线图的知识进行解答.
14.数据共50个,分别落在5个小组内,第一、二、三、四组的数据分别为2、8、15、14,则第五个小组的频数为( )
A.14
B.15
C.10
D.11
答案:D
解析:解答:根据题意,得
第二组数的频数为50-(2+8+15+14)=11.
故选:D.
分析:此题只需根据各小组频数之和等于数据总和,进行计算求出答案.
15.小红统计了她家3月份的电话通话时间,并绘制成如下的频数分布表(表中数据含最大值但不含最小值):
通话时间(min) 0~2 2~4 4~6 6~8 8~10
通话次数 26 12 8 5 3
那么小红家3月份电话通话时间不超过6min的频数是( )
A.3
B.8
C.38
D.46
答案:D
解析:解答:小红家3月份电话通话时间不超过6min的频数是:26+12+8=46.
故选:D.
分析:根据频数是指每个小组内对象出现的次数进行计算得到答案.
二、填空题
16.某样本有100个数据分成五组.第一、二组频数之和为25,第三组频数是35.第四、五组频数相等,则第五组频数是
答案:20
解析:解答:第四、五组频数的和是:100-25-35=40,则第五组的频数是20.
故答案为:20.
分析:根据各个组的频数的和是100进行计算求解.
17.小明和小华做抛掷两枚硬币的游戏,确定“发现两个正面”为成功,各抛10次,实验记录如下:
则小华的成功率为 ,两人的平均成功率为 .
实验结果的频数 小华 小明
两个正面的频数 3 1
不是两个正面的频数 7 9
答案:30%|20%
解析:解答:小华的成功率为:=30%;两人的平均成功率为:=20%.
故答案为:30%;20%.
分析:小华的两个正面的频数除以总频数就等于他的成功率;两人的两个正面的频数和除以他们的总频数和等于两人的平均成功率.
18.某校七年级(2)班50名学生进行一分钟跳绳测试,将所得数据整理后,得到落在180次~189次区间的百分比为28%,则在180次~189次区间的人数是
答案:14
解析:解答:50×28%=14(人),所以在180次~189次区间的人数是14人.
故答案为:14.
分析:根据频数的求法:频数=频数之和×百分比,计算可得答案.
19.在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是
分组 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
频数 9 15 ? 16 12
答案:28
解析:解答:样本容量=第五组的频数÷第五组的百分比=12÷15%=80;
第三小组(69.5~79.5)的频数=80-9-15-16-12=28.
故答案为:28.
分析:先根据总数=第五组的频数÷第五组占的百分比求得总数,再由第三组的频数=总数-其余四个小组的频数计算求解.
20.如图,一项统计数据的频数分布直方图中,如果直方图关于第三组的小长方形呈轴对称图形(坐标轴忽略不计),那么,落在110~130这一组中的频数是
答案:300
解析:解答:如果直方图关于第三组的小长方形呈轴对称图形,则110~130这一组与第二组频数应相等,故其频数为300.
故答案为:300.
分析:由于频数直方图成轴对称图形,所以110~130这一组与第二组频数应该相等.
三、解答题
21.如图是若干名同学在引体向上训练时一次测试成绩(个)的频数分布折线图.
(1)参加这次测试共有多少名同学?
答案:23
解答:2+4+5+10+2=23名;
(2)组中点为9个一组的频数是多少?
答案:10
解答:组中点为9个一组的频数是10;
(3)分布两端虚设的频数为零的是哪两组?
答案:4.5~5.5|10.5~11.5
解答:分布两端虚设的频数为零的两组是4.5~5.5和10.5~11.5.
解析:分析:(1)根据图中的信息,找到符合条件的数据,再进一步计算;(2)观察即可得出组中点为9个一组的频数;(3)仔细观察,得出正确答案.
22.某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:
(1)该班共有多少名学生参加这次测验?
答案:48
解答:(1)根据题意,得
该班参加测验的学生人数为3+6+9+12+18=48(名),
答:该班参加测验的学生有48名;
(2)求60.5~70.5这一分数段的频数是多少?
答案:12
解答:读图可得:60.5~70.5这一分数段的频数为12;
(3)若80分以上为优秀,则该班的优秀率是多少?
答案:31%
解答:读图可得:该班的优秀人数为:9+6=15;
则该班的优秀率为:(9+6)÷48×100%≈31%;
答:该班的优秀率是31%.
解析:分析:(1)根据频率分布直方图中,各组频数之和为总人数;将统计图中的数据进行求和计算可得答案;(2)观察频数直方图,根据频数的定义直接得到答案;(3)首先分析直方图可得80分以上的优秀人数,再除以总人数进一步计算百分比.
23.统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频数分布直方图(部分未完成):
上海世博会前20天日参观人数的频数分布表:
组别(万人) 组中值(万人) 频数
7.5~14.5 11 5
14.5~21.5 6
21.5~28.5 25
28.5~35.5 32 3
上海世博会前20天日参观人数的频数分布直方图:
(1)请补全频数分布表和频数分布直方图;
答案:解答:组中值:(14.5+21.5)÷2=18,频数:20-5-6-3=6
上海世博会前20天日参观人数的频数分布表:
组别(万人) 组中值(万人) 频数
7.5~14.5 11 5
14.5~21.5 18 6
21.5~28.5 25 6
28.5~35.5 32 3
上海世博会前20天日参观人数的频数分布直方图:
(2)求出日参观人数不低于22万的天数和所占的百分比;
答案:9|45%
解答:依题意得,日参观人数不低于22万有6+3=9天,
所占百分比为9÷20=45%.
解析:分析:(1)根据表格的数据求出14.5~21.5小组的组中值,21.5~28.5小组的频数,最后补全频数分布表和频数分布直方图;(2)根据表格知道日参观人数不低于22万的天数有两个小组,共9天,除以总人数求出所占的百分比.
24.某面粉批发商通过统计前48个星期的面粉销售量(单位:吨),对数据适当分组后,列出了如下频数分布表:
销售量 18.5~19.5 19.5~20.5 20.5~21.5 21.5~22.5 22.5~23.5 23.5~24.5 合计
频数 6 7 9 12 8 6 48
在下面图中分别画出频数分布直方图和频数折线图.
答案:解答:如图:
解析:分析:根据频数分布直方折和频数折线图的作法,结合题中所给的数据,作出频数分布直方图和频数折线图.
25.九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
分数段(分) 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
组中值(分) 54.5 64.5 74.5 84.5 94.5
频数 a 9 10 14 5
所占百分比 5% 22.5% 25.0% 35.0% b
(1)频数分布表中a=______,b=______;
答案:2|0.125
解答:解答:(1)频数分布表中,由于×100%=40(人),则a=40×0.050=2(人),
b=1-0.05-0.225-0.25-0.35=0.125;
(2)画频数分布直方图;
答案:如图所示:
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
答案:1050元
解答:由表得,有29名同学获得一等奖或二等奖,
设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意,得
15x+10(29-x)=335,
解得x=9,
∴50x+30(29-x)=1050.
所以他们得到的奖金是1050元.
解析:分析:(1)由成绩频数分布表可以看出,b=1-0.05-0.225-0.25-0.35=0.125;由已知组的频数占总数的百分比及频数求出总数,用总数乘0.050求出a的值;(2)由数据补全直方图;(3)由表得,有29名同学获得一等奖或二等奖;设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得关系式15x+10(29-x)=335可求得x的值;再根据关系式50x+30(29-x)可求得获得的奖金.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
北师大版数学七年级上册第6章第3节数据的表示同步检测
一、选择题
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数
B.等于数据总数
C.大于数据总数
D.不能确定
答案:B
解析:解答:由于各小组的频数之和等于数据总数,所以选项B正确.
故选:B.
分析:根据在频数分布表的绘制方法,各小组的频数之和等于数据的总数进行选择.
2.调查某小区内30户居民月人均收入情况,制成如下的频数分布直方图,收入在1200~1240元的频数是( )
A.12
B.13
C.14
D.15
答案:C
解析:解答:根据题意可知:共30户接受调查,其中1200以下的有3+7=10户,1400以上的有4+1+1=6户;那么收入在1200~1240元的频数是30-6-10=14.
故选:C.
分析:从图中得出1200以下和1400以上的频数,则收入在1200~1240元的频数=30-1200以下的频数-1400以上的频数.
3.容量100的样本数据,按从小到大的顺序分8组,如表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
第三组的频数是( )
A.14
B.13
C.12
D.10
答案:A
解析:解答:∵由容量100的样本数据知有100个数,而其他组的数的个数都是已知的,
∴频数为100-(10+13+14+14+13+12+90)=14.
故选:A.
分析:由容量100的样本数据知有100个数,而其他组的数的个数都是已知的,因此得到要求的频数.
4.如图是若干只电灯泡的使用寿命进行检测的频数分布折线图,由图可知检测的频数为( )
A.20
B.14
C.12
D.10
答案:A
解析:解答:由图可知:检测的频数为(2+4+8+6)=20.
故选:A.
分析:根据各个数据对应的频数,相加计算得到检测的频数.
题型:单选题
5.在“We like maths.”这个句子的所有字母中,字母“e”出现的频数是( )
A.5
B.4
C.3
D.2
答案:D
解析:解答:在“We like maths.”这个句子的所有字母中,字母“e”出现了2次,故字母“e”出现的频数为2.
故选:D.
分析:数出这个句子中字母“e”出现的次数即可得到答案.
6.随机抽查了某校七年级63名学生的身高(单位:cm),所得到的数据中最大值是172,最小值是149、若取组距为4,则这些数据可分成( )组.
A.5
B.6
C.7
D.8
答案:B
解析:解答:(172-149)÷4=23÷4≈6组.
故选:B.
分析:计算最大值与最小值的差,除以组距进行求得.
7.抛硬币15次,有6次出现正面,9次出现反面,则出现正面的频数是( )
A.6
B.9
C.15
D.3
答案:A
解析:解答:抛硬币15次,有6次出现正面,9次出现反面,则出现正面的频数是6.
故选:A.
分析:根据频数的概念进行选择,频数是表示一组数据中,符合条件的对象出现的次数.
8.以下表格是某校初一(1)班班长候选人得票数领先的三位同学的得票情况,则小明得票的频数是( )
候选人 小红 小明 小丽
唱票记录 正正正一 正 正正正正正一
A.16
B.5
C.21
D.42
答案:B
解析:解答:根据小明得到唱票记录可得小明得票的频数是5.
故选:B.
分析:此题须根据小明得到唱票记录得出小明得票的频数.
9.一个射手连续射靶10次,其中1次射中10环,6次射中9环,3次射中8环,则射中( )环的频数最大.
A.6
B.8
C.9
D.10
答案:C
解析:解答:根据题意,可知6次射中9环,次数最多;所以射中9环的频数最大.
故选:C.
分析:根据各个频数,进行比较得出最大值.
10.一年中,31号出现的频数是( )
A.7
B.6
C.5
D.12
答案:A
解析:解答:一年中,有7个月有31天,所以一年中,31出现的频数是7.
故选:A.
分析:根据频数的概念,结合一年中,有几个月是31天可以得到答案.
11.大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90-110这一组的频数是( )
A.2
B.4
C.6
D.14
答案:B
解析:解答:跳绳次数在90~110之间的数据有91,93,100,102四个,所以频数为4.
故选:B.
分析:根据频数的定义,从数据中数出在90~110这一组的数据个数即可得到答案.
12.一组数据的最小数是12,最大数是38,如果分组的组距相等,且组距为3,则分组后的第一组为( )
A.11.5~13.5
B.11.5~14.5
C.12.5~14.5
D.12.5~15.5
答案:B
解析:因为这组数据的最小数是12,所以第一组应从11.5开始,因为12.5>12,故排除C、D;又组距为3,所以分组后的第一组为11.5~14.5.
故选:B.
分析:先由这组数据的最小数是12,排除C、D,再根据组距为3,进一步得出答案.
13.下列说法正确的是( )
A.样本的数据个数等于频数之和
B.扇形统计图可以告诉我们各部分的数量分别是多少
C.如果一组数据可以用扇形统计图表示,那么它一定可以用频数分布直方图表示
D.将频数分布直方图中小长方形上面一边的一个端点顺次连接起来,就可以得到频数折线图
答案:A
解析:解答:样本的数据个数相当于样本容量,频数之和等于样本容量,所以选项A正确;
扇形统计图只可以得到各部分数据的比例,不能得到各部分的数量,所以选项B错误;
作扇形统计图只要知道各部分的比例就行,频数分布直方图必须知道各部分的数量,所以选项C错误;
将直方图上方边的中点顺序连接起来可以得到频数折线图,所以选项D错误.
故选:A.
分析:根据频数、频数分布直方图、频数折线图的知识进行解答.
14.数据共50个,分别落在5个小组内,第一、二、三、四组的数据分别为2、8、15、14,则第五个小组的频数为( )
A.14
B.15
C.10
D.11
答案:D
解析:解答:根据题意,得
第二组数的频数为50-(2+8+15+14)=11.
故选:D.
分析:此题只需根据各小组频数之和等于数据总和,进行计算求出答案.
15.小红统计了她家3月份的电话通话时间,并绘制成如下的频数分布表(表中数据含最大值但不含最小值):
通话时间(min) 0~2 2~4 4~6 6~8 8~10
通话次数 26 12 8 5 3
那么小红家3月份电话通话时间不超过6min的频数是( )
A.3
B.8
C.38
D.46
答案:D
解析:解答:小红家3月份电话通话时间不超过6min的频数是:26+12+8=46.
故选:D.
分析:根据频数是指每个小组内对象出现的次数进行计算得到答案.
二、填空题
16.某样本有100个数据分成五组.第一、二组频数之和为25,第三组频数是35.第四、五组频数相等,则第五组频数是
答案:20
解析:解答:第四、五组频数的和是:100-25-35=40,则第五组的频数是20.
故答案为:20.
分析:根据各个组的频数的和是100进行计算求解.
17.小明和小华做抛掷两枚硬币的游戏,确定“发现两个正面”为成功,各抛10次,实验记录如下:
则小华的成功率为 ,两人的平均成功率为 .
实验结果的频数 小华 小明
两个正面的频数 3 1
不是两个正面的频数 7 9
答案:30%|20%
解析:解答:小华的成功率为:=30%;两人的平均成功率为:=20%.
故答案为:30%;20%.
分析:小华的两个正面的频数除以总频数就等于他的成功率;两人的两个正面的频数和除以他们的总频数和等于两人的平均成功率.
18.某校七年级(2)班50名学生进行一分钟跳绳测试,将所得数据整理后,得到落在180次~189次区间的百分比为28%,则在180次~189次区间的人数是
答案:14
解析:解答:50×28%=14(人),所以在180次~189次区间的人数是14人.
故答案为:14.
分析:根据频数的求法:频数=频数之和×百分比,计算可得答案.
19.在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是
分组 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
频数 9 15 ? 16 12
答案:28
解析:解答:样本容量=第五组的频数÷第五组的百分比=12÷15%=80;
第三小组(69.5~79.5)的频数=80-9-15-16-12=28.
故答案为:28.
分析:先根据总数=第五组的频数÷第五组占的百分比求得总数,再由第三组的频数=总数-其余四个小组的频数计算求解.
20.如图,一项统计数据的频数分布直方图中,如果直方图关于第三组的小长方形呈轴对称图形(坐标轴忽略不计),那么,落在110~130这一组中的频数是
答案:300
解析:解答:如果直方图关于第三组的小长方形呈轴对称图形,则110~130这一组与第二组频数应相等,故其频数为300.
故答案为:300.
分析:由于频数直方图成轴对称图形,所以110~130这一组与第二组频数应该相等.
三、解答题
21.如图是若干名同学在引体向上训练时一次测试成绩(个)的频数分布折线图.
(1)参加这次测试共有多少名同学?
答案:23
解答:2+4+5+10+2=23名;
(2)组中点为9个一组的频数是多少?
答案:10
解答:组中点为9个一组的频数是10;
(3)分布两端虚设的频数为零的是哪两组?
答案:4.5~5.5|10.5~11.5
解答:分布两端虚设的频数为零的两组是4.5~5.5和10.5~11.5.
解析:分析:(1)根据图中的信息,找到符合条件的数据,再进一步计算;(2)观察即可得出组中点为9个一组的频数;(3)仔细观察,得出正确答案.
22.某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:
(1)该班共有多少名学生参加这次测验?
答案:48
解答:(1)根据题意,得
该班参加测验的学生人数为3+6+9+12+18=48(名),
答:该班参加测验的学生有48名;
(2)求60.5~70.5这一分数段的频数是多少?
答案:12
解答:读图可得:60.5~70.5这一分数段的频数为12;
(3)若80分以上为优秀,则该班的优秀率是多少?
答案:31%
解答:读图可得:该班的优秀人数为:9+6=15;
则该班的优秀率为:(9+6)÷48×100%≈31%;
答:该班的优秀率是31%.
解析:分析:(1)根据频率分布直方图中,各组频数之和为总人数;将统计图中的数据进行求和计算可得答案;(2)观察频数直方图,根据频数的定义直接得到答案;(3)首先分析直方图可得80分以上的优秀人数,再除以总人数进一步计算百分比.
23.统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频数分布直方图(部分未完成):
上海世博会前20天日参观人数的频数分布表:
组别(万人) 组中值(万人) 频数
7.5~14.5 11 5
14.5~21.5 6
21.5~28.5 25
28.5~35.5 32 3
上海世博会前20天日参观人数的频数分布直方图:
(1)请补全频数分布表和频数分布直方图;
答案:解答:组中值:(14.5+21.5)÷2=18,频数:20-5-6-3=6
上海世博会前20天日参观人数的频数分布表:
组别(万人) 组中值(万人) 频数
7.5~14.5 11 5
14.5~21.5 18 6
21.5~28.5 25 6
28.5~35.5 32 3
上海世博会前20天日参观人数的频数分布直方图:
(2)求出日参观人数不低于22万的天数和所占的百分比;
答案:9|45%
解答:依题意得,日参观人数不低于22万有6+3=9天,
所占百分比为9÷20=45%.
解析:分析:(1)根据表格的数据求出14.5~21.5小组的组中值,21.5~28.5小组的频数,最后补全频数分布表和频数分布直方图;(2)根据表格知道日参观人数不低于22万的天数有两个小组,共9天,除以总人数求出所占的百分比.
24.某面粉批发商通过统计前48个星期的面粉销售量(单位:吨),对数据适当分组后,列出了如下频数分布表:
销售量 18.5~19.5 19.5~20.5 20.5~21.5 21.5~22.5 22.5~23.5 23.5~24.5 合计
频数 6 7 9 12 8 6 48
在下面图中分别画出频数分布直方图和频数折线图.
答案:解答:如图:
解析:分析:根据频数分布直方折和频数折线图的作法,结合题中所给的数据,作出频数分布直方图和频数折线图.
25.九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
分数段(分) 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
组中值(分) 54.5 64.5 74.5 84.5 94.5
频数 a 9 10 14 5
所占百分比 5% 22.5% 25.0% 35.0% b
(1)频数分布表中a=______,b=______;
答案:2|0.125
解答:解答:(1)频数分布表中,由于×100%=40(人),则a=40×0.050=2(人),
b=1-0.05-0.225-0.25-0.35=0.125;
(2)画频数分布直方图;
答案:如图所示:
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
答案:1050元
解答:由表得,有29名同学获得一等奖或二等奖,
设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意,得
15x+10(29-x)=335,
解得x=9,
∴50x+30(29-x)=1050.
所以他们得到的奖金是1050元.
解析:分析:(1)由成绩频数分布表可以看出,b=1-0.05-0.225-0.25-0.35=0.125;由已知组的频数占总数的百分比及频数求出总数,用总数乘0.050求出a的值;(2)由数据补全直方图;(3)由表得,有29名同学获得一等奖或二等奖;设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得关系式15x+10(29-x)=335可求得x的值;再根据关系式50x+30(29-x)可求得获得的奖金.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
