第 3 章评估检测题(A卷) 单元测试 (无答案) 九年级下册数学北师版
文档属性
| 名称 | 第 3 章评估检测题(A卷) 单元测试 (无答案) 九年级下册数学北师版 |  | |
| 格式 | docx | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 20:22:41 | ||
图片预览

文档简介
第 3 章评估检测题(A卷)
(时间 :120分钟 满分 :100分)
1. 选择题(每题 3 分 ,共 24分)
(1)如图 3-1所示 , 已知正方形的边长为 1,若圆与正方形的四条边都相切 ,则阴影部分 的面积最接近( ) .
A.0.1 B.0.2
C.0.3 D.0.4
(2)下列图形中 ,对称轴最多的是( ) . 图 3-1
A. 圆 B. 正方形 C. 正三角形 D. 线段
(3)如图 3-2所示 ,在 ☉O 中 ,半径 OD⊥弦 AB 于点 C,连接 AO 并延长交 ☉O 于点 E,连接 EC. 若 AB = 8,CD= 2,则 EC的长度为( ) .
B.8
(4)关于圆 ,下列命题中正确的是( ) .
(
图
3-2
)A. 若圆心到两条直线的距离都等于圆的半径 ,则这两条直线不可能垂直
B. 若圆心到两条直线的距离都小于圆的半径 ,则这两条直线与圆一定有 4个公共点
C. 若两条弦所在直线不平行 ,则这两条弦可能在圆内有公共点
D. 若两条弦平行 ,则这两条弦之间的距离一定小于圆的半径
(5)如图 3-3所示 ,△ABC的边 AC与 ☉O相交于 C,D 两点,且经过圆心 O,边 AB 与 ☉O 相切 ,切点为
B. 已知 ∠A= 30°,则 ∠C的大小是( ) .
A.30° B.45° C.60° D.40°
(6)如图 3-4所示 , 已知线段 OA 交 ☉O 于点 B,且 OB=AB,点 P 是 ☉O上的一个动点,那么 ∠OAP 的 最大值是( ) .
A.30° B.45° C.60° D.90°
(7)如图 3-5所示 ,在正五边形 ABCDE中 ,连接 AC,AD,CE,CE 交 AD 于点 F,连接 BF,BF与 AC相 交于点 M. 下列说法中不正确的是( ) .
A.△CDF的周长等于 AD+CD B.FC平分 ∠BFD
C.AC2 +BF2 = 4CD2 D.DE2 =EF ·CE
(8)如图 3-6所示,点 P 为 ☉O 的直径 BA 延长线上一点,PC 与 ☉O 相切 ,切点为 C,点 D 是 ☉O 上 一 点,连接 PD, 已知 PC= PD=BC. 现有下列结论 : ①PD 与 ☉O 相切 ; ②四边形 PCBD 是菱形 ; ③PO=AB; ④∠PDB= 120°. 其中正确的个数为( ) .
A.4个 B.3个 C.2个 D.1个
1
图 3-3
图 3-4
图 3-5
图 3-6
2. 填空题(每题 2 分 ,共 20分)
(1)在平面内 , ☉O 的半径为 5 cm,点 P 到圆心 O的距离为 3 cm ,则点 P 与 ☉O 的位置关系是
.
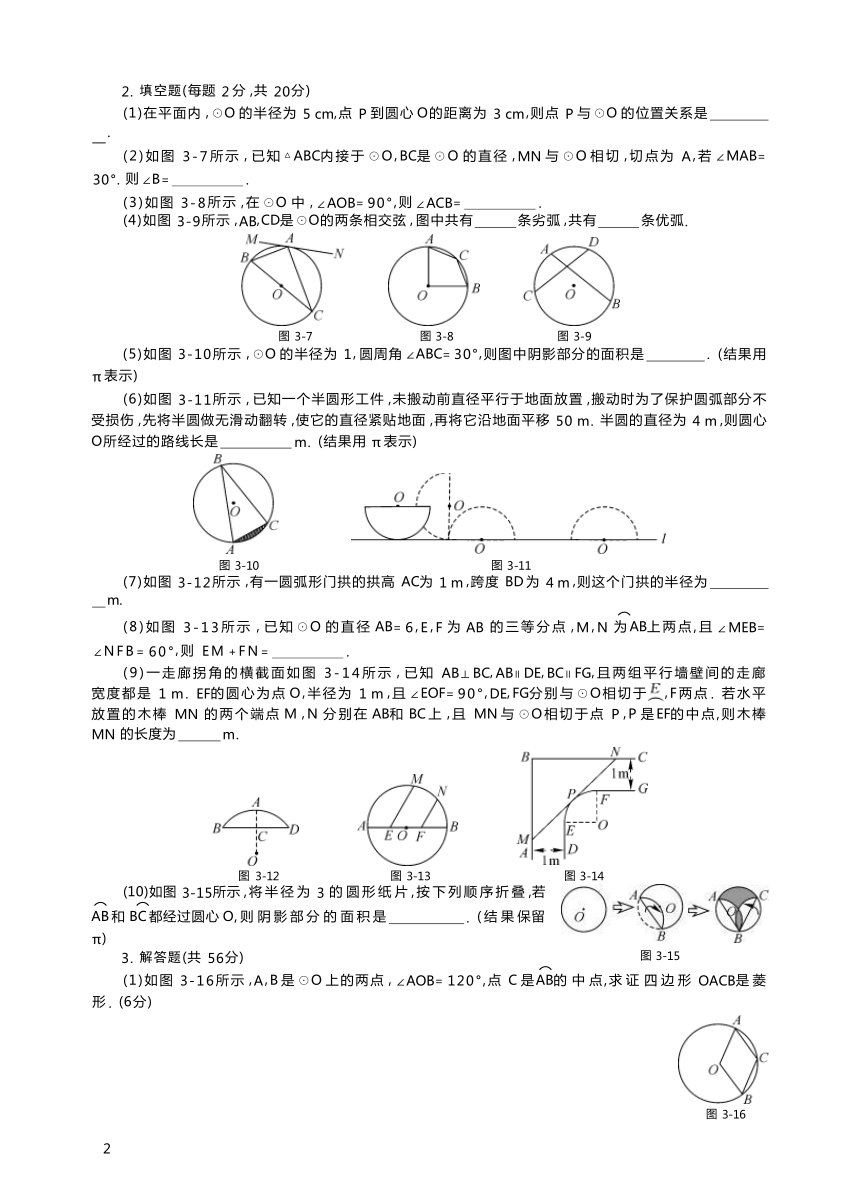
(2)如图 3-7所示 , 已知 △ABC内接于 ☉O,BC是 ☉O 的直径 ,MN 与 ☉O 相切 ,切点为 A,若 ∠MAB= 30°. 则 ∠B= .
(3)如图 3-8所示 ,在 ☉O 中 , ∠AOB= 90°,则 ∠ACB= .
(4)如图 3-9所示 ,AB,CD是 ☉O的两条相交弦 , 图中共有 条劣弧 ,共有 条优弧.
图 3-7 图 3-8 图 3-9
(5)如图 3-10所示 , ☉O 的半径为 1, 圆周角 ∠ABC= 30°,则图中阴影部分的面积是 . (结果用 π 表示)
(6)如图 3-11所示 , 已知一个半圆形工件 ,未搬动前直径平行于地面放置 ,搬动时为了保护圆弧部分不 受损伤 ,先将半圆做无滑动翻转 ,使它的直径紧贴地面 ,再将它沿地面平移 50 m. 半圆的直径为 4 m ,则圆心 O所经过的路线长是 m. (结果用 π 表示)
图 3-10 图 3-11
(7)如图 3-12所示 ,有一圆弧形门拱的拱高 AC为 1 m ,跨度 BD 为 4 m ,则这个门拱的半径为
(
︵
) m.
(8)如图 3-13所示 , 已知 ☉O 的直径 AB= 6,E,F 为 AB 的三等分点 ,M,N 为AB上两点,且 ∠MEB= ∠NFB= 60°,则 EM +FN= .
(9)一走廊拐角的横截面如图 3-14所示 , 已知 AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊 宽度都是 1 m. EF的圆心为点 O,半径为 1 m ,且 ∠EOF= 90°,DE,FG分别与 ☉O相切于,F两点 . 若水平 放置的木棒 MN 的两个端点 M ,N 分别在 AB和 BC 上 ,且 MN 与 ☉O相切于点 P ,P 是EF的中点,则木棒 MN 的长度为 m.
图 3-12 图 3-13 图 3-14
2
(10)如图 3-15所示 , 将 半 径 为 3 的 圆 形 纸 片 , 按 下 列 顺 序 折 叠 ,若
︵ ︵
AB 和 BC 都经过圆心 O, 则 阴 影 部 分 的 面 积 是 . ( 结 果 保留 π)
3. 解答题(共 56分)
图 3-15
(
︵
)(1)如图 3-16所示 ,A,B 是 ☉O 上的两点 , ∠AOB= 120°,点 C 是AB的 中 点,求 证 四 边 形 OACB是 菱 形 . (6分)
图 3-16
(2)如图 3-17所示 , 已知等腰 △ABC,AB=AC= 8, ∠BAC= 120°,请用圆规和直尺作出 △ABC的外接 圆 ,并计算此外接圆的半径 . (7分)
图 3-17
(3)如图 3-18所示 , ☉O的直径 AB与弦 CD相交于点 E, 已知 AE= 1,BE= 5, ∠DEB= 60°,求弦 CD 的长 . (7分)
图 3-18
(4)如图 3-19所示 , ☉O的直径 AB为 10 cm ,弦 BC为 6 cm,点 D,E分别是 ∠ACB的平分线与 ☉O和 AB的交点,点 P 为 AB延长线上一点,且 PC= PE. (8分)
①求 AC,AD 的长 .
②试判断直线 PC与 ☉O的位置关系 ,并说明理由 .
图 3-19
(5)利用已知半径的球可以测量圆柱形管子的内径 . 小明把半径为 5 cm 的小皮球置于保温杯口上 ,画出 了草图(见图 3-20) . 请你根据图中的数据 ,帮助小明计算出保温杯的内径 . (8分)
图 3-20
(6)如图 3-21所示 , ☉O1 的 圆 心 在 ☉O的 圆 周 上 , ☉O和 ☉O1 交 于 点 A,B,AC 切 ☉O 于 点 A, 连 接
3
CB,BD 是 ☉O的直径 , ∠D= 40°,求 ∠AO1B, ∠ACB和 ∠CAD的度数 . (10分)
图 3-21
(7)如图 3-22所示 ,在 Rt△ABC中 , ∠C= 90°,°∠BAC= 60°,AB= 8. 半径为 3的 ☉M 与射线BA 相切 ,
切点为 N,且 AN= 3. 将 Rt△ABC顺时针旋转 120后得到 Rt△ADE,点 B,C的对应点分别是点 D ,E. (10
分)
①画出旋转后的 Rt△ADE.
②求出 Rt△ADE的直角边 DE被 ☉M 截得的弦 PQ的长度 .
③判断 Rt△ADE的斜边 AD所在的直线与 ☉M 的位置关系 ,并说明理由 .
图 3-22
4
(时间 :120分钟 满分 :100分)
1. 选择题(每题 3 分 ,共 24分)
(1)如图 3-1所示 , 已知正方形的边长为 1,若圆与正方形的四条边都相切 ,则阴影部分 的面积最接近( ) .
A.0.1 B.0.2
C.0.3 D.0.4
(2)下列图形中 ,对称轴最多的是( ) . 图 3-1
A. 圆 B. 正方形 C. 正三角形 D. 线段
(3)如图 3-2所示 ,在 ☉O 中 ,半径 OD⊥弦 AB 于点 C,连接 AO 并延长交 ☉O 于点 E,连接 EC. 若 AB = 8,CD= 2,则 EC的长度为( ) .
B.8
(4)关于圆 ,下列命题中正确的是( ) .
(
图
3-2
)A. 若圆心到两条直线的距离都等于圆的半径 ,则这两条直线不可能垂直
B. 若圆心到两条直线的距离都小于圆的半径 ,则这两条直线与圆一定有 4个公共点
C. 若两条弦所在直线不平行 ,则这两条弦可能在圆内有公共点
D. 若两条弦平行 ,则这两条弦之间的距离一定小于圆的半径
(5)如图 3-3所示 ,△ABC的边 AC与 ☉O相交于 C,D 两点,且经过圆心 O,边 AB 与 ☉O 相切 ,切点为
B. 已知 ∠A= 30°,则 ∠C的大小是( ) .
A.30° B.45° C.60° D.40°
(6)如图 3-4所示 , 已知线段 OA 交 ☉O 于点 B,且 OB=AB,点 P 是 ☉O上的一个动点,那么 ∠OAP 的 最大值是( ) .
A.30° B.45° C.60° D.90°
(7)如图 3-5所示 ,在正五边形 ABCDE中 ,连接 AC,AD,CE,CE 交 AD 于点 F,连接 BF,BF与 AC相 交于点 M. 下列说法中不正确的是( ) .
A.△CDF的周长等于 AD+CD B.FC平分 ∠BFD
C.AC2 +BF2 = 4CD2 D.DE2 =EF ·CE
(8)如图 3-6所示,点 P 为 ☉O 的直径 BA 延长线上一点,PC 与 ☉O 相切 ,切点为 C,点 D 是 ☉O 上 一 点,连接 PD, 已知 PC= PD=BC. 现有下列结论 : ①PD 与 ☉O 相切 ; ②四边形 PCBD 是菱形 ; ③PO=AB; ④∠PDB= 120°. 其中正确的个数为( ) .
A.4个 B.3个 C.2个 D.1个
1
图 3-3
图 3-4
图 3-5
图 3-6
2. 填空题(每题 2 分 ,共 20分)
(1)在平面内 , ☉O 的半径为 5 cm,点 P 到圆心 O的距离为 3 cm ,则点 P 与 ☉O 的位置关系是
.
(2)如图 3-7所示 , 已知 △ABC内接于 ☉O,BC是 ☉O 的直径 ,MN 与 ☉O 相切 ,切点为 A,若 ∠MAB= 30°. 则 ∠B= .
(3)如图 3-8所示 ,在 ☉O 中 , ∠AOB= 90°,则 ∠ACB= .
(4)如图 3-9所示 ,AB,CD是 ☉O的两条相交弦 , 图中共有 条劣弧 ,共有 条优弧.
图 3-7 图 3-8 图 3-9
(5)如图 3-10所示 , ☉O 的半径为 1, 圆周角 ∠ABC= 30°,则图中阴影部分的面积是 . (结果用 π 表示)
(6)如图 3-11所示 , 已知一个半圆形工件 ,未搬动前直径平行于地面放置 ,搬动时为了保护圆弧部分不 受损伤 ,先将半圆做无滑动翻转 ,使它的直径紧贴地面 ,再将它沿地面平移 50 m. 半圆的直径为 4 m ,则圆心 O所经过的路线长是 m. (结果用 π 表示)
图 3-10 图 3-11
(7)如图 3-12所示 ,有一圆弧形门拱的拱高 AC为 1 m ,跨度 BD 为 4 m ,则这个门拱的半径为
(
︵
) m.
(8)如图 3-13所示 , 已知 ☉O 的直径 AB= 6,E,F 为 AB 的三等分点 ,M,N 为AB上两点,且 ∠MEB= ∠NFB= 60°,则 EM +FN= .
(9)一走廊拐角的横截面如图 3-14所示 , 已知 AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊 宽度都是 1 m. EF的圆心为点 O,半径为 1 m ,且 ∠EOF= 90°,DE,FG分别与 ☉O相切于,F两点 . 若水平 放置的木棒 MN 的两个端点 M ,N 分别在 AB和 BC 上 ,且 MN 与 ☉O相切于点 P ,P 是EF的中点,则木棒 MN 的长度为 m.
图 3-12 图 3-13 图 3-14
2
(10)如图 3-15所示 , 将 半 径 为 3 的 圆 形 纸 片 , 按 下 列 顺 序 折 叠 ,若
︵ ︵
AB 和 BC 都经过圆心 O, 则 阴 影 部 分 的 面 积 是 . ( 结 果 保留 π)
3. 解答题(共 56分)
图 3-15
(
︵
)(1)如图 3-16所示 ,A,B 是 ☉O 上的两点 , ∠AOB= 120°,点 C 是AB的 中 点,求 证 四 边 形 OACB是 菱 形 . (6分)
图 3-16
(2)如图 3-17所示 , 已知等腰 △ABC,AB=AC= 8, ∠BAC= 120°,请用圆规和直尺作出 △ABC的外接 圆 ,并计算此外接圆的半径 . (7分)
图 3-17
(3)如图 3-18所示 , ☉O的直径 AB与弦 CD相交于点 E, 已知 AE= 1,BE= 5, ∠DEB= 60°,求弦 CD 的长 . (7分)
图 3-18
(4)如图 3-19所示 , ☉O的直径 AB为 10 cm ,弦 BC为 6 cm,点 D,E分别是 ∠ACB的平分线与 ☉O和 AB的交点,点 P 为 AB延长线上一点,且 PC= PE. (8分)
①求 AC,AD 的长 .
②试判断直线 PC与 ☉O的位置关系 ,并说明理由 .
图 3-19
(5)利用已知半径的球可以测量圆柱形管子的内径 . 小明把半径为 5 cm 的小皮球置于保温杯口上 ,画出 了草图(见图 3-20) . 请你根据图中的数据 ,帮助小明计算出保温杯的内径 . (8分)
图 3-20
(6)如图 3-21所示 , ☉O1 的 圆 心 在 ☉O的 圆 周 上 , ☉O和 ☉O1 交 于 点 A,B,AC 切 ☉O 于 点 A, 连 接
3
CB,BD 是 ☉O的直径 , ∠D= 40°,求 ∠AO1B, ∠ACB和 ∠CAD的度数 . (10分)
图 3-21
(7)如图 3-22所示 ,在 Rt△ABC中 , ∠C= 90°,°∠BAC= 60°,AB= 8. 半径为 3的 ☉M 与射线BA 相切 ,
切点为 N,且 AN= 3. 将 Rt△ABC顺时针旋转 120后得到 Rt△ADE,点 B,C的对应点分别是点 D ,E. (10
分)
①画出旋转后的 Rt△ADE.
②求出 Rt△ADE的直角边 DE被 ☉M 截得的弦 PQ的长度 .
③判断 Rt△ADE的斜边 AD所在的直线与 ☉M 的位置关系 ,并说明理由 .
图 3-22
4
