17.1 勾股定理 第2课时 同步练习 2024--2025学年初中数学人教版版八年级下册
文档属性
| 名称 | 17.1 勾股定理 第2课时 同步练习 2024--2025学年初中数学人教版版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:48:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
17.1 勾股定理 第2课时 同步练习
2024--2025学年初中数学人教版版八年级下册
一、单选题
1.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A. B. C. D.
2.如图,学校操场上有两棵树和(都与水平地面垂直),大树高8米,树梢D到树的水平距离的长度为8米,小树高2米,一只小鸟从树梢D飞到树梢B,则它至少要飞行的长度为( )
A.8米 B.10米 C.12米 D.16米
3.有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.设这根芦苇的长度为x尺,则可列方程( )
A. B. C. D.
4.如图,一架25分米长的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底部7分米,如果梯子的顶端沿墙下滑4分米,那么梯子的底端将向外平滑( )
A.9分米 B.15分米 C.5分米 D.8分米
5.年月日是第七个中国农民丰收节,小彬用打印机制作了一个底面周长为,高为的圆柱粮仓模型,如图,现要在此模型的侧面贴彩色装饰带,使装饰带从柱底沿圆柱表面均匀地缠绕圈到达柱顶正上方(从点到点,为的中点),则装饰带的长度最短为( )
A. B. C. D.
6.《九章算术》勾股章中有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.向水深、葭长各几何”.其大意为:有一个水池,其水面是边长为1丈的正方形(即丈尺),在水池正中央有一根芦苇,它高出水面的部分为1尺(即尺).如果把这根芦苇拉向岸边,它的顶端恰好到达池边水面点处,则芦苇的长是( )
A.10尺 B.12尺 C.13尺 D.15尺
7.题目:“在和中,两个三角形的高线分别为和,,,,,且.已知,求的度数.”对于其答案,甲答:,乙答:,丙答:,则正确的是( )
A.只有甲答的对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
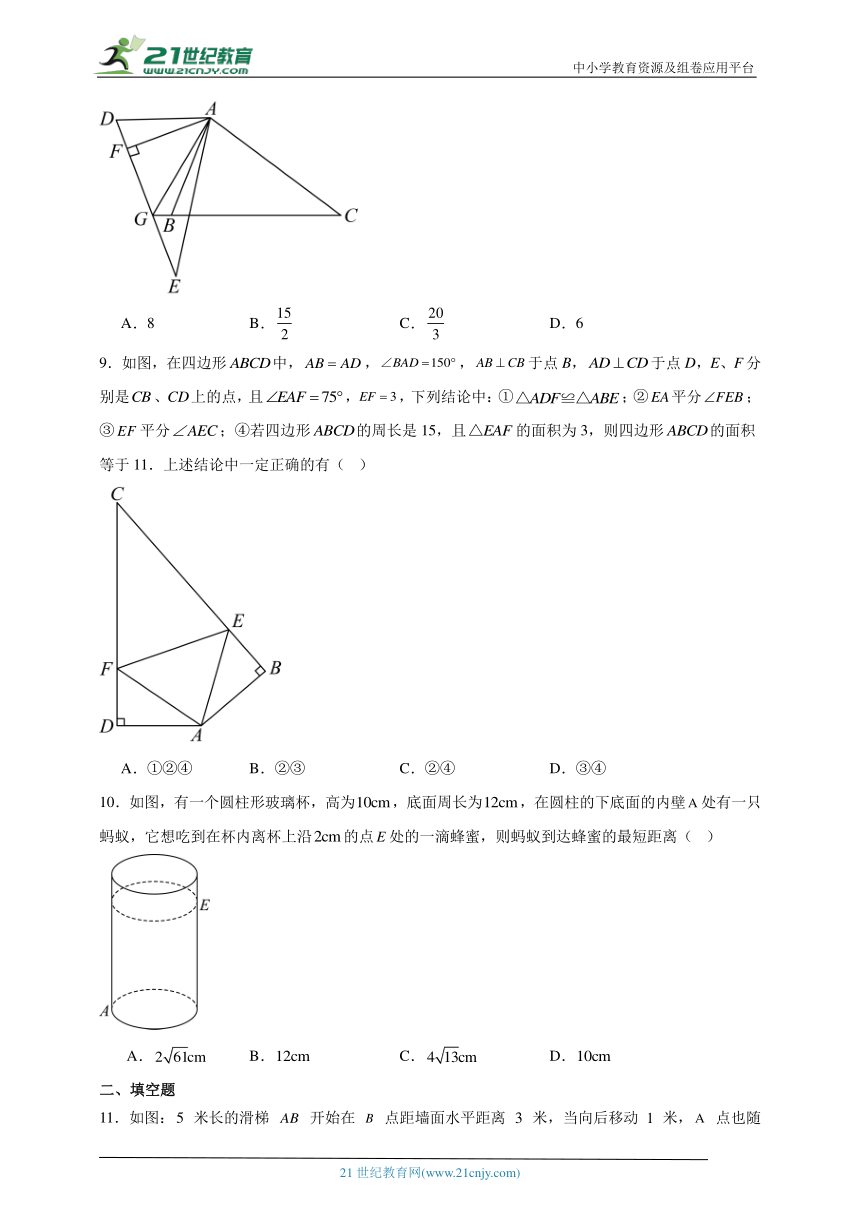
8.如图,在和中,,,,过作,垂足为,交的延长线于点,连接.四边形的面积为64,.则的长是( )
A.8 B. C. D.6
9.如图,在四边形中,,,于点B,于点D,E、F分别是、上的点,且,,下列结论中:①;②平分;③平分;④若四边形的周长是15,且的面积为3,则四边形的面积等于11.上述结论中一定正确的有( )
A.①②④ B.②③ C.②④ D.③④
10.如图,有一个圆柱形玻璃杯,高为,底面周长为,在圆柱的下底面的内壁处有一只蚂蚁,它想吃到在杯内离杯上沿的点处的一滴蜂蜜,则蚂蚁到达蜂蜜的最短距离( )
A. B. C. D.
二、填空题
11.如图: 米长的滑梯 开始在 点距墙面水平距离 米,当向后移动 米, 点也随着向下滑一段距离,则下滑的距离 (大于、小于或等于) 米.
12.如图,风雨过后一棵大树被折断,折断处离地面的高度为,倒下后树顶端着地点距树底端的距离为,一只蜗牛从树顶端的处出发,以的速度沿树干向上爬行,则它爬到折断处所需的时间为 .
13.如图,,,若判断的依据是“”,还需要添加的一个条件是 .(只要写出一种情况即可)
14.如图是一张直角三角形纸片,两直角边,将折叠,顶点与点重合,折痕为,则的长为 .
15.如图,已知钓鱼杆的长为5米,露在水面上的鱼线长为3米,某钓鱼者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线长度为4米,则的长为 米.
16.如图所示,点、在线段上,、相交于点,,且,若用“”判定和全等,则需添加的条件是 .
三、解答题
17.如图,中,,,,将折叠,使点与的中点重合,折痕为,求线段的长.
18.如图有一个四级台阶,它的每一级的长、宽分别为18分米、4分米.
(1)如果给台阶表面8个矩形区域铺上定制红毯,需要定制红毯的面积为432平方分米,那么每一级台阶的高为多少分米?
(2)A和C是这个台阶上两个相对的端点,台阶角落点A处有一只蚂蚁,想到台阶顶端点C处去吃美味的食物,则蚂蚁沿着台阶面从点A爬行到点C的最短路程为多少分米?
19.为了让学生更好地学会用勾股定理,某校八年级数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题,利用课余时间完成了实践调查,并利用皮尺等工具采集了如下的实验数据.
【采集数据】
如图,利用皮尺测量水平距离米,然后根据手中剩余风筝线的长度得出风筝线的长度米,最后测量放风筝的小康同学的身高米
【数据应用】
当点均在同一平面内,已知图中各点均在同一平面内,点,,,在同一直线上.
(1)求此时风筝的垂直高度.
(2)若站在点不动,想把风筝沿着的方向从点的位置上升18米到点的位置,则还需要放出风筝线多少米?
20.如图,分别是、上的点,分别是上的点,若、,求证:.
参考答案
1.B
本题考查了折叠的性质,勾股定理,三角形的面积,解题的关键是掌握折叠的性质.由折叠可得,再根据勾股定理求出,最后根据三角形的面积公式即可求解.
解:由折叠可得:,
,,
,
,
故选:B.
2.B
本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.连接,求出米,然后由勾股定理求出的长即可.
解:如图,连接,
在中,(米),
∴(米),
即小鸟至少要飞行的长度为10米.
故选:B.
3.C
本题考查的是勾股定理的实际应用;由芦苇长为尺,可得水深为尺,再利用两条直角边的平方和等于斜边建立方程即可解答.
解:如图,
设芦苇长为尺,则水深为尺,
由题意得,,
故选:C.
4.D
本题考查勾股定理的应用.掌握直角三角形三边之间满足两直角边的平方和等于斜边的平方是解决此题的关键.注意:整个过程中,梯子的长度不变.
先利用勾股定理求出,再根据顶端下滑4分米求出,根据勾股定理求出,即可得出底部平滑的距离.
解:在中,根据勾股定理
分米,
当梯子的顶端沿墙下滑4分米时,梯子的顶部距离墙底端距离:分米,
在中根据勾股定理
分米,
则梯子的底部将向外平滑距离:分米.
故选:D
5.A
本题考查了勾股定理的展开图求最短距离问题,画出圆柱的展开图,连接,由勾股定理即可求解,正确画出展开图是解题的关键.
解:如图,圆柱的侧面展开图为长方形,连接,
∴即为最短,
∴,,
∴,
故选:.
6.C
本题考查正确勾股定理的应用.找到题中的直角三角形,设水深为x尺,根据勾股定理解答.
解:设水深为尺,则芦苇长为尺,
根据勾股定理得:,即,
解得:,
芦苇的长度(尺),
答:芦苇长13尺.
故选:C.
7.B
本题考查了全等三角形的判定和性质,本题要分两种情况求出,一种情况是,此时可得:;另一种情况是当在内部,在外部时,此时可得:,
解:如下图所示,
当时,;
如下图所示,
当在内部,在外部时,
,,
,
,
,
要把甲和丙的答案合在一起才完整.
故选:B.
8.A
过点作于点,利用可证得,于是可得,利用三角形的面积公式可得,利用可证得,于是可得,同理可证得,于是可得,于是可推出,因而可得,据此即可求出的长.
解:如图,过点作于点,
在和中,
,
,
,
又,
,
,
,,
,
在和中,
,
,
,
同理:,
,
,
,
,
故选:.
9.C
本题考查了全等三角形的性质和判定定理,角平分线的定义,三角形的三边关系定理,垂直定义等知识点,延长到G,使,连接,,根据全等三角形的判定定理求出,根据全等三角形的性质得出,,,求出,根据全等三角形的判定定理得出,根据全等三角形的性质得出,,,再进行判断即可.
解:延长到G,使,连接,,
∵,,
∴,
在和中
,
∴,
∴,,,
∵,,
∴,
∴,
∴,
在和中
,
∴,
∴,,,
∴平分,故②正确;
根据已知不能推出,平分,故①③不正确;
在和中,
,
∴,
∴,
设,,
∵四边形的周长是15,
∴,
∵的面积为3,
∴,
∴,
∴,
∴四边形的面积,故④正确;
综上,正确的有②④.
故选:C.
10.D
本题考查了勾股定理的应用最短距离,将杯子侧面展开,连接,则的长为蚂蚁到达蜂蜜的最短距离,利用勾股定理求出即可求解,找出蚂蚁到达蜂蜜的最短路径是解题的关键.
解:如图,将杯子侧面展开,连接,则的长为蚂蚁到达蜂蜜的最短距离,
由题意得,,,,
∴,
∴蚂蚁到达蜂蜜的最短距离为,
故选:.
11.等于
本题主要考查勾股定理的应用,勾股定理:两直角边的平方和等于斜边的平方.
直接利用勾股定理得出的长,进而求出的长,即可得出答案.
解:由题意可得:,
故,
∵当向后移动 1 米,
,
,
则.
故下滑的距离为 1 米,
故答案为:等于.
12.
本题考查的是勾股定理的应用,根据勾股定理求出的长是解答此题的关键.
由勾股定理求出的长,即可解决问题.
解:在中,,,
,
,
即爬到折断处所需的时间为,
故答案为:
13.或(只要写出一种情况即可)
本题主要考查了全等三角形的判定,已知,,可得,,为公共边,根据“”,添加一直角边即可证明,熟练掌握全等三角形的判定方法并能灵活运用是解决此题的关键.
解:,,
,,
,
∴添加或,即可用“”证明,
故答案为:或(只要写出一种情况即可).
14.
本题考查了折叠的性质,勾股定理,运用勾股定理建立方程求出是关键;由折叠知,则,在中由勾股定理建立方程,即可求出,在中由勾股定理即可求得结果.
解:,
;
由折叠知,
则;
在中,,
即,
解得:;
在中,由勾股定理得.
故答案为:.
15.1
本题主要考查了勾股定理的应用,根据勾股定理分别求出和,再根据即可得出答案,根据勾股定理求出和是解题的关键.
在中,,,
∴,
在中,,,
∴,
∴,
故答案为:1.
16.
本题考查全等三角形的判定.根据题目中的条件知一对直角边相等,再添加斜边相等可以用“”判断.
解:∵,
∴,
∴,
∵,
当添加条件时,,
故答案为:.
17.
本题考查勾股定理与折叠问题,折叠得到,设,在中,利用勾股定理进行求解即可.
解:∵折叠,
∴,
∵为的中点,
∴,
设,则:,
∵,
∴由勾股定理,得:,
解得:;
∴.
18.(1)每一级台阶的高为2分米.
(2)蚂蚁沿着台阶面从点A爬行到点C的最短路程为30分米.
(1)设每一级台阶的高为x分米,根据题意列方程即可得到结论;
(2)先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
(1)解:设每一级台阶的高为x分米,
根据题意得,18×(4+x)×4=432,
解得x=2,
答:每一级台阶的高为2分米;
(2)四级台阶平面展开图为长方形,长为18分米,宽为(2+4)×4=24分米,
则蚂蚁沿台阶面从点A爬行到C点最短路程是此长方形的对角线长.
由勾股定理得:AC=(分米),
答:蚂蚁沿着台阶面从点A爬行到点C的最短路程为30分米.
19.(1)米
(2)14米
本题主要考查了勾股定理的实际应用:
(1)根据题意可得米,再由勾股定理求出的长即可得到答案;
(2)先求出的长,再利用勾股定理求出的长即可得到答案.
(1)解:由题意得,米,,
在中,由勾股定理得米,
∴米;
∴此时风筝的垂直高度为米;
(2)解:由题意得,米,
在中,由勾股定理得米,
∵米,
∴还需要放出风筝线14米.
20.见解析
本题考查了全等三角形的判定,掌握全等三角形的判定定理是解题关键.利用“”证明全等即可.
证明:、,
在和中,
,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
17.1 勾股定理 第2课时 同步练习
2024--2025学年初中数学人教版版八年级下册
一、单选题
1.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A. B. C. D.
2.如图,学校操场上有两棵树和(都与水平地面垂直),大树高8米,树梢D到树的水平距离的长度为8米,小树高2米,一只小鸟从树梢D飞到树梢B,则它至少要飞行的长度为( )
A.8米 B.10米 C.12米 D.16米
3.有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.设这根芦苇的长度为x尺,则可列方程( )
A. B. C. D.
4.如图,一架25分米长的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底部7分米,如果梯子的顶端沿墙下滑4分米,那么梯子的底端将向外平滑( )
A.9分米 B.15分米 C.5分米 D.8分米
5.年月日是第七个中国农民丰收节,小彬用打印机制作了一个底面周长为,高为的圆柱粮仓模型,如图,现要在此模型的侧面贴彩色装饰带,使装饰带从柱底沿圆柱表面均匀地缠绕圈到达柱顶正上方(从点到点,为的中点),则装饰带的长度最短为( )
A. B. C. D.
6.《九章算术》勾股章中有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.向水深、葭长各几何”.其大意为:有一个水池,其水面是边长为1丈的正方形(即丈尺),在水池正中央有一根芦苇,它高出水面的部分为1尺(即尺).如果把这根芦苇拉向岸边,它的顶端恰好到达池边水面点处,则芦苇的长是( )
A.10尺 B.12尺 C.13尺 D.15尺
7.题目:“在和中,两个三角形的高线分别为和,,,,,且.已知,求的度数.”对于其答案,甲答:,乙答:,丙答:,则正确的是( )
A.只有甲答的对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
8.如图,在和中,,,,过作,垂足为,交的延长线于点,连接.四边形的面积为64,.则的长是( )
A.8 B. C. D.6
9.如图,在四边形中,,,于点B,于点D,E、F分别是、上的点,且,,下列结论中:①;②平分;③平分;④若四边形的周长是15,且的面积为3,则四边形的面积等于11.上述结论中一定正确的有( )
A.①②④ B.②③ C.②④ D.③④
10.如图,有一个圆柱形玻璃杯,高为,底面周长为,在圆柱的下底面的内壁处有一只蚂蚁,它想吃到在杯内离杯上沿的点处的一滴蜂蜜,则蚂蚁到达蜂蜜的最短距离( )
A. B. C. D.
二、填空题
11.如图: 米长的滑梯 开始在 点距墙面水平距离 米,当向后移动 米, 点也随着向下滑一段距离,则下滑的距离 (大于、小于或等于) 米.
12.如图,风雨过后一棵大树被折断,折断处离地面的高度为,倒下后树顶端着地点距树底端的距离为,一只蜗牛从树顶端的处出发,以的速度沿树干向上爬行,则它爬到折断处所需的时间为 .
13.如图,,,若判断的依据是“”,还需要添加的一个条件是 .(只要写出一种情况即可)
14.如图是一张直角三角形纸片,两直角边,将折叠,顶点与点重合,折痕为,则的长为 .
15.如图,已知钓鱼杆的长为5米,露在水面上的鱼线长为3米,某钓鱼者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线长度为4米,则的长为 米.
16.如图所示,点、在线段上,、相交于点,,且,若用“”判定和全等,则需添加的条件是 .
三、解答题
17.如图,中,,,,将折叠,使点与的中点重合,折痕为,求线段的长.
18.如图有一个四级台阶,它的每一级的长、宽分别为18分米、4分米.
(1)如果给台阶表面8个矩形区域铺上定制红毯,需要定制红毯的面积为432平方分米,那么每一级台阶的高为多少分米?
(2)A和C是这个台阶上两个相对的端点,台阶角落点A处有一只蚂蚁,想到台阶顶端点C处去吃美味的食物,则蚂蚁沿着台阶面从点A爬行到点C的最短路程为多少分米?
19.为了让学生更好地学会用勾股定理,某校八年级数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题,利用课余时间完成了实践调查,并利用皮尺等工具采集了如下的实验数据.
【采集数据】
如图,利用皮尺测量水平距离米,然后根据手中剩余风筝线的长度得出风筝线的长度米,最后测量放风筝的小康同学的身高米
【数据应用】
当点均在同一平面内,已知图中各点均在同一平面内,点,,,在同一直线上.
(1)求此时风筝的垂直高度.
(2)若站在点不动,想把风筝沿着的方向从点的位置上升18米到点的位置,则还需要放出风筝线多少米?
20.如图,分别是、上的点,分别是上的点,若、,求证:.
参考答案
1.B
本题考查了折叠的性质,勾股定理,三角形的面积,解题的关键是掌握折叠的性质.由折叠可得,再根据勾股定理求出,最后根据三角形的面积公式即可求解.
解:由折叠可得:,
,,
,
,
故选:B.
2.B
本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.连接,求出米,然后由勾股定理求出的长即可.
解:如图,连接,
在中,(米),
∴(米),
即小鸟至少要飞行的长度为10米.
故选:B.
3.C
本题考查的是勾股定理的实际应用;由芦苇长为尺,可得水深为尺,再利用两条直角边的平方和等于斜边建立方程即可解答.
解:如图,
设芦苇长为尺,则水深为尺,
由题意得,,
故选:C.
4.D
本题考查勾股定理的应用.掌握直角三角形三边之间满足两直角边的平方和等于斜边的平方是解决此题的关键.注意:整个过程中,梯子的长度不变.
先利用勾股定理求出,再根据顶端下滑4分米求出,根据勾股定理求出,即可得出底部平滑的距离.
解:在中,根据勾股定理
分米,
当梯子的顶端沿墙下滑4分米时,梯子的顶部距离墙底端距离:分米,
在中根据勾股定理
分米,
则梯子的底部将向外平滑距离:分米.
故选:D
5.A
本题考查了勾股定理的展开图求最短距离问题,画出圆柱的展开图,连接,由勾股定理即可求解,正确画出展开图是解题的关键.
解:如图,圆柱的侧面展开图为长方形,连接,
∴即为最短,
∴,,
∴,
故选:.
6.C
本题考查正确勾股定理的应用.找到题中的直角三角形,设水深为x尺,根据勾股定理解答.
解:设水深为尺,则芦苇长为尺,
根据勾股定理得:,即,
解得:,
芦苇的长度(尺),
答:芦苇长13尺.
故选:C.
7.B
本题考查了全等三角形的判定和性质,本题要分两种情况求出,一种情况是,此时可得:;另一种情况是当在内部,在外部时,此时可得:,
解:如下图所示,
当时,;
如下图所示,
当在内部,在外部时,
,,
,
,
,
要把甲和丙的答案合在一起才完整.
故选:B.
8.A
过点作于点,利用可证得,于是可得,利用三角形的面积公式可得,利用可证得,于是可得,同理可证得,于是可得,于是可推出,因而可得,据此即可求出的长.
解:如图,过点作于点,
在和中,
,
,
,
又,
,
,
,,
,
在和中,
,
,
,
同理:,
,
,
,
,
故选:.
9.C
本题考查了全等三角形的性质和判定定理,角平分线的定义,三角形的三边关系定理,垂直定义等知识点,延长到G,使,连接,,根据全等三角形的判定定理求出,根据全等三角形的性质得出,,,求出,根据全等三角形的判定定理得出,根据全等三角形的性质得出,,,再进行判断即可.
解:延长到G,使,连接,,
∵,,
∴,
在和中
,
∴,
∴,,,
∵,,
∴,
∴,
∴,
在和中
,
∴,
∴,,,
∴平分,故②正确;
根据已知不能推出,平分,故①③不正确;
在和中,
,
∴,
∴,
设,,
∵四边形的周长是15,
∴,
∵的面积为3,
∴,
∴,
∴,
∴四边形的面积,故④正确;
综上,正确的有②④.
故选:C.
10.D
本题考查了勾股定理的应用最短距离,将杯子侧面展开,连接,则的长为蚂蚁到达蜂蜜的最短距离,利用勾股定理求出即可求解,找出蚂蚁到达蜂蜜的最短路径是解题的关键.
解:如图,将杯子侧面展开,连接,则的长为蚂蚁到达蜂蜜的最短距离,
由题意得,,,,
∴,
∴蚂蚁到达蜂蜜的最短距离为,
故选:.
11.等于
本题主要考查勾股定理的应用,勾股定理:两直角边的平方和等于斜边的平方.
直接利用勾股定理得出的长,进而求出的长,即可得出答案.
解:由题意可得:,
故,
∵当向后移动 1 米,
,
,
则.
故下滑的距离为 1 米,
故答案为:等于.
12.
本题考查的是勾股定理的应用,根据勾股定理求出的长是解答此题的关键.
由勾股定理求出的长,即可解决问题.
解:在中,,,
,
,
即爬到折断处所需的时间为,
故答案为:
13.或(只要写出一种情况即可)
本题主要考查了全等三角形的判定,已知,,可得,,为公共边,根据“”,添加一直角边即可证明,熟练掌握全等三角形的判定方法并能灵活运用是解决此题的关键.
解:,,
,,
,
∴添加或,即可用“”证明,
故答案为:或(只要写出一种情况即可).
14.
本题考查了折叠的性质,勾股定理,运用勾股定理建立方程求出是关键;由折叠知,则,在中由勾股定理建立方程,即可求出,在中由勾股定理即可求得结果.
解:,
;
由折叠知,
则;
在中,,
即,
解得:;
在中,由勾股定理得.
故答案为:.
15.1
本题主要考查了勾股定理的应用,根据勾股定理分别求出和,再根据即可得出答案,根据勾股定理求出和是解题的关键.
在中,,,
∴,
在中,,,
∴,
∴,
故答案为:1.
16.
本题考查全等三角形的判定.根据题目中的条件知一对直角边相等,再添加斜边相等可以用“”判断.
解:∵,
∴,
∴,
∵,
当添加条件时,,
故答案为:.
17.
本题考查勾股定理与折叠问题,折叠得到,设,在中,利用勾股定理进行求解即可.
解:∵折叠,
∴,
∵为的中点,
∴,
设,则:,
∵,
∴由勾股定理,得:,
解得:;
∴.
18.(1)每一级台阶的高为2分米.
(2)蚂蚁沿着台阶面从点A爬行到点C的最短路程为30分米.
(1)设每一级台阶的高为x分米,根据题意列方程即可得到结论;
(2)先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
(1)解:设每一级台阶的高为x分米,
根据题意得,18×(4+x)×4=432,
解得x=2,
答:每一级台阶的高为2分米;
(2)四级台阶平面展开图为长方形,长为18分米,宽为(2+4)×4=24分米,
则蚂蚁沿台阶面从点A爬行到C点最短路程是此长方形的对角线长.
由勾股定理得:AC=(分米),
答:蚂蚁沿着台阶面从点A爬行到点C的最短路程为30分米.
19.(1)米
(2)14米
本题主要考查了勾股定理的实际应用:
(1)根据题意可得米,再由勾股定理求出的长即可得到答案;
(2)先求出的长,再利用勾股定理求出的长即可得到答案.
(1)解:由题意得,米,,
在中,由勾股定理得米,
∴米;
∴此时风筝的垂直高度为米;
(2)解:由题意得,米,
在中,由勾股定理得米,
∵米,
∴还需要放出风筝线14米.
20.见解析
本题考查了全等三角形的判定,掌握全等三角形的判定定理是解题关键.利用“”证明全等即可.
证明:、,
在和中,
,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
