17.1 勾股定理 第3课时 同步练习 2024--2025学年初中数学人教版版八年级下册
文档属性
| 名称 | 17.1 勾股定理 第3课时 同步练习 2024--2025学年初中数学人教版版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 17:48:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
17.1 勾股定理 第3课时 同步练习
2024--2025学年初中数学人教版版八年级下册
一、单选题
1.如图所示的网格是正方形网格,图形的各个顶点均为格点,则的度数是( )
A. B. C. D.
2.如图在的网格中,每个小正方形的边长均为2,则B到直线的距离为( )
A. B. C. D.
3.在平面直角坐标系中,点,点,x轴上取一点C使为等腰直角三角形(为斜边),则点C坐标为( )
A. B. C. D.
4.如图,在的网格中,以为一边,点在格点处,使为等腰三角形的点有( )
A.1个 B.2个 C.3个 D.4个
5.如图,已知正方形的面积为5,点A在数轴上,且表示的数为.现以点A为圆心,以的长为半径画圆,所得圆和数轴交于点E(E在A的右侧),则点E表示的数为( )
A. B. C. D.
6.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
7.如图,在中,,,,点D为AB的中点,点E为AC上一点,把沿DE折叠得到,连接.若,则的长为( )
A. B. C.4 D.
8.如图,方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,下列结论正确的有( )个;
①的形状是等腰三角形;
②的周长是;
③点C到边的距离是.
A.0个 B.1个 C.2个 D.3个
9.如图,在的正方形网格中,每个小正方形边长为1,点均为格点,以为圆心,长为半径作弧,交网格线于点,则两点间的距离为( )
A. B. C. D.
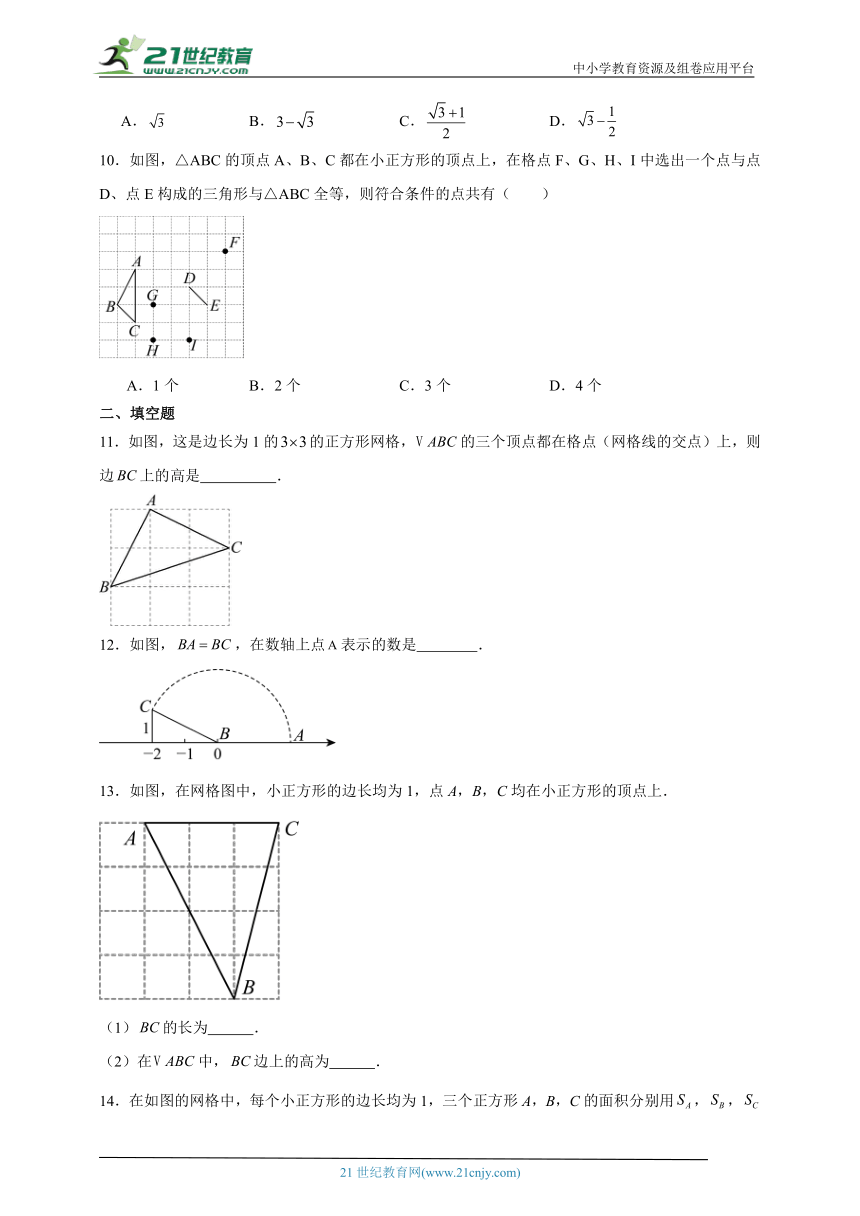
10.如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,这是边长为1的的正方形网格,的三个顶点都在格点(网格线的交点)上,则边上的高是 .
12.如图,,在数轴上点表示的数是 .
13.如图,在网格图中,小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
(1)的长为 .
(2)在中,边上的高为 .
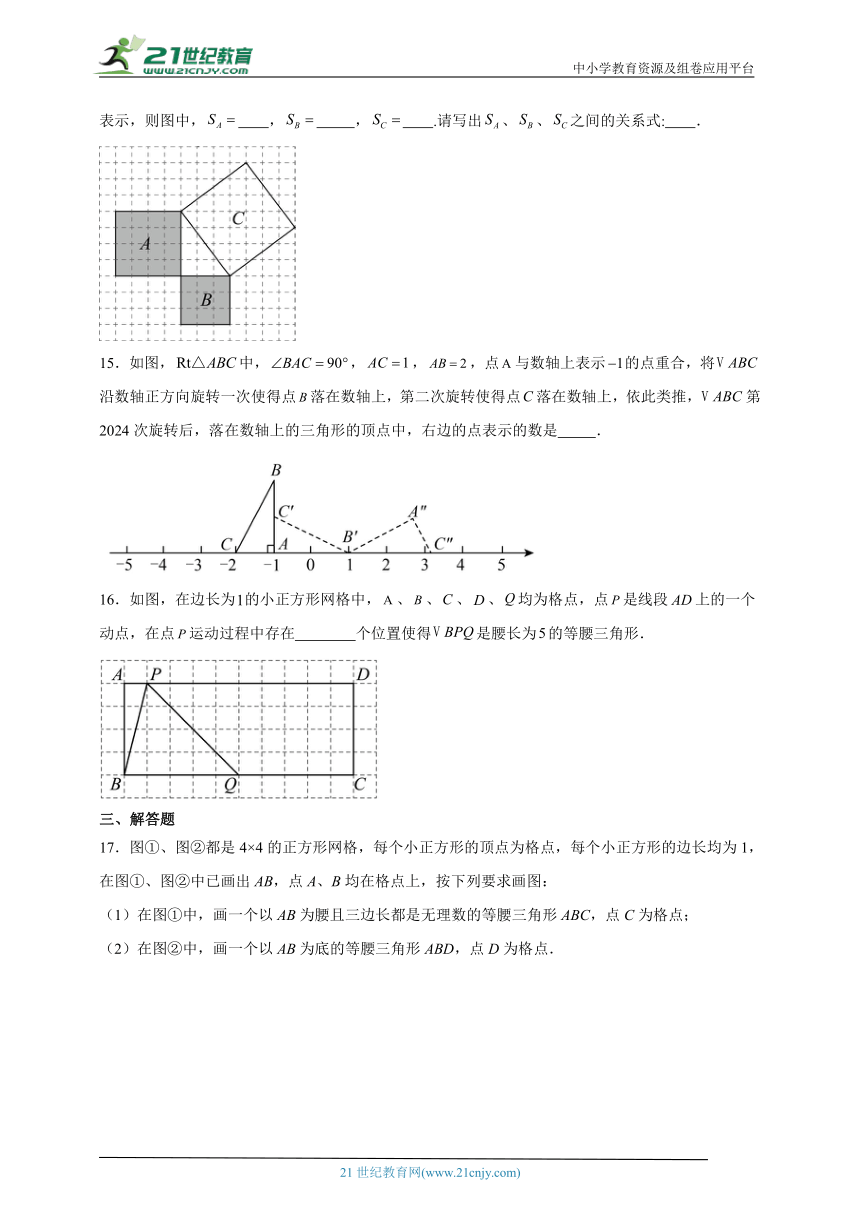
14.在如图的网格中,每个小正方形的边长均为1,三个正方形A,B,C的面积分别用,,表示,则图中, , , .请写出、、之间的关系式: .
15.如图,中,,,,点与数轴上表示的点重合,将沿数轴正方向旋转一次使得点落在数轴上,第二次旋转使得点落在数轴上,依此类推,第2024次旋转后,落在数轴上的三角形的顶点中,右边的点表示的数是 .
16.如图,在边长为的小正方形网格中,、、、、均为格点,点是线段上的一个动点,在点运动过程中存在 个位置使得是腰长为的等腰三角形.
三、解答题
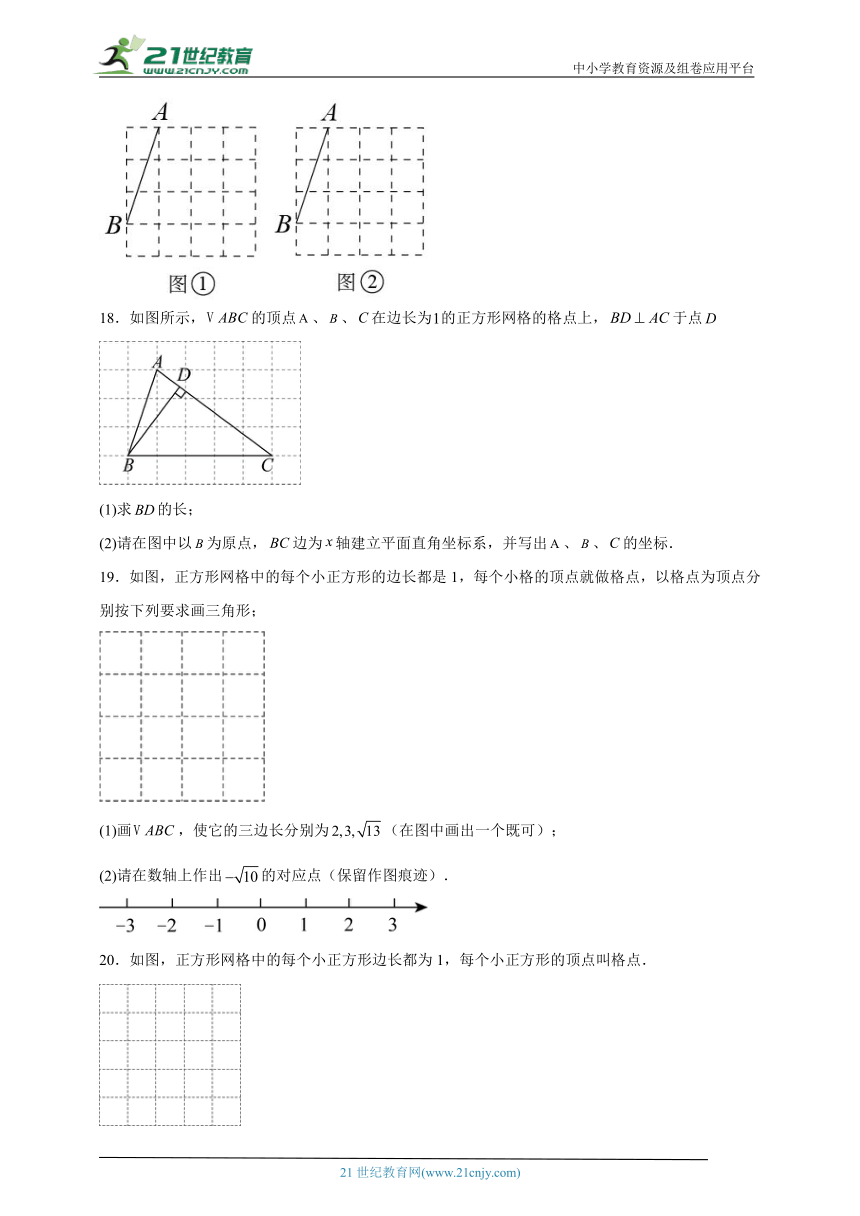
17.图①、图②都是4×4的正方形网格,每个小正方形的顶点为格点,每个小正方形的边长均为1,在图①、图②中已画出AB,点A、B均在格点上,按下列要求画图:
(1)在图①中,画一个以AB为腰且三边长都是无理数的等腰三角形ABC,点C为格点;
(2)在图②中,画一个以AB为底的等腰三角形ABD,点D为格点.
18.如图所示,的顶点、、在边长为的正方形网格的格点上,于点
(1)求的长;
(2)请在图中以为原点,边为轴建立平面直角坐标系,并写出、、的坐标.
19.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点就做格点,以格点为顶点分别按下列要求画三角形;
(1)画,使它的三边长分别为(在图中画出一个既可);
(2)请在数轴上作出的对应点(保留作图痕迹).
20.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点.
(1)以格点为顶点画,使三边长为:3,,;
(2)求的面积.
21.小正方形网格中,三个顶点均在格点上的三角形叫做格点三角形.设每个小正方形边长为1.如下图,格点,
(1)图中格点的面积是_______;
(2)按要求画图:
①在图1中画一个与全等且有一条公共边的格点三角形;
②在图2中画一个与全等且只有唯一公共点A的格点三角形;
③在图3中画一个面积为5的格点直角三角形且直角边为网格图中的斜格点线段.
参考答案
1.A
本题考查了网格与勾股定理,全等三角形的判定和性质,等腰三角形的判定和性质,掌握网格的特点,全等三角形的判定和性质是解题的关键.
根据题意可证,得到,则有,由网格的性质可得是等腰直角三角形,,由此即可求解.
解:如图所示,
∵网格是正方形网格,
∴,,,
∴,
∴,
∴,
∴,
在中,,
∴是等腰直角三角形,
∴,
∴,
故选:A .
2.D
此题考查了勾股定理,二次根式的性质,以及三角形的面积,熟练掌握勾股定理是解本题的关键.
根据小正方形的边长为1,利用勾股定理求出,由正方形面积减去三个直角三角形面积求出三角形面积,利用面积法求出边上的高即可.
解:如图,为边上的高,
,
,,
,
解得:.
故选:B.
3.C
本题主要考查了勾股定理与坐标系,根据题意正确画出图形是解题的关键.
先根据题意画出符合条件的,然后直接确定点C的坐标即可.
解:根据题意画出等腰直角(为斜边)如下,易得点C坐标为.
故选C.
4.D
本题考查了格点与勾股定理,等腰三角形,掌握等腰三角形的定义和性质是解题的关键.
根据网格的特点,勾股定理,等腰三角形的定义和性质作图即可求解.
解:如图所示,,
∵,
∴是等腰三角形,
∴点为所求点;
∵,,,
∴是等腰三角形,
∴点为所求点;
综上所述,点有4个,
故选:D .
5.A
本题主要考查实数与数轴及两点间距离,根据两点间距离及点的位置判断出点所表示的数是解题的关键.
根据正方形的边长是面积的算术平方根得,再根据勾股定理可得,再结合A点所表示的数及间距离可得点E所表示的数.
解:∵正方形的面积为5,
∴,
∴
∵点A表示的数是,且点E在点A的右侧,
∴点E表示的数为.
故选:A.
6.B
本题考查了数轴与实数及勾股定理.根据图示,可得:点A是以为圆心,以为半径的圆与数轴的交点,再根据两点间的距离的求法,求出a的值为多少即可.
解:由勾股定理得:,
∴,
∴点A是以为圆心,以为半径的圆与数轴的交点,且在左侧,
∴.
故选:B.
7.D
过点A作AF⊥DE于点F,由直角三角形的性质可得AF=1,AE=,即可求A'E,EC的长,由勾股定理可求A'C的长.
解:如图,过点A作AF⊥DE于点F,
∵AB=4,点D为AB的中点,
∴AD=2,
∵∠ADE=30°,AF⊥DE,
∴AF=1,∠FAD=60°,
∵∠BAC=105°,
∴∠FAE=45°,AF⊥DE,
∴∠AEF=45°=∠EAF,
∴AF=EF=1,
∴AE=,
∴EC=AC-AE=2,
∵把△ADE沿DE折叠得到△A'DE,
∴∠AEA'=2∠AEF=90°,A'E=AE=,
∴A'C=,
故选D.
8.B
根据勾股定理求出、、长,即可判断①和②,根据三角形面积公式即可判断③.
解:由勾股定理得:,,,
∴,
∴的形状是等腰三角形,
∴①正确;
的周长是,
∴②错误;
设C到的距离是h,
由三角形面积公式得:,
∵,
∴,
∴③错误;
故选:B.
9.B
如图:连接AE,则AE=2、AD=1,由勾股定理可求出DE,然后运用线段的和差即可解答.
解:如图:连接AE,则AE=2,AD=1
∴DE=
∴CE=CD-DE=.
故选B.
10.B
分析:根据全等三角形的判定解答即可.
详解:由图形可知:AB=,AC=3,BC=,GD=,DE=,GE=3,DI=3,EI=,所以G,I两点与点D、点E构成的三角形与△ABC全等.
故选B.
点睛:本题考查了全等三角形的判定,关键是根据SSS证明全等三角形.
11.
本题考查了勾股定理以及三角形面积等知识,设边上的高为h,由勾股定理求出的长,再由割补法求出的面积,即可解决问题.
解:设边上的高为h,
由勾股定理得:,
∵,
∴,
∴,
即边上的高为,
故答案为:.
12.
本题考查了勾股定理的应用和实数与数轴,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.利用勾股定理求得的长度,然后结合数轴求得表示的数.
解:由图形可知,,
在数轴上,点表示的数为,点在点右侧.
在数轴上点表示的数是,
故答案为:.
13. /
此题考查了勾股定理,三角形的面积公式,关键是根据三角形的面积公式列出方程.
(1)根据勾股定理即可,
(2)根据三角形的面积公式列出方程进行计算即可.
解:(1);
故答案为:
(2)设边上的高为,
,
,
故答案为:.
14. 16 9 25
本题考查了网格中的正方形与勾股定理应用,熟练掌握正方形的面积与勾股定理的光线是解题的关键.
依题意,16,,
∵在如图的网格中,每个小正方形的边长均为1,
∴根据勾股定理,得正方形C的边长为,
∴
∵16,,,
∴.
故答案为:16,9,25,.
15.
本题考查了实数与数轴的对应关系,勾股定理,解决本题的关键是熟练掌握实数与数轴的关系.根据题意的三个顶点按的顺序依次落在数轴上,每三次一个循环,一个循环中在数轴上第一个点到第三个的长为的周长,很容易求出它的周长为.因为,所以2024次旋转共经历674个循环还余2,第2024次旋转后,落在数轴上的三角形的顶点中,右边的是点C,再求解即可.
解:中,,,,
.
的周长为.
有三个顶点,
次旋转中每三次一个循环.
,
次旋转共经历674个循环还余2.
第2024次旋转后,落在数轴上的三角形的顶点中,右边的是点C,
次旋转后点C共向右移动的总长为.
第一次的起点为,
右边的点表示的数是.
故答案为:.
16.
本题主要考查等腰三角形的判定,学会分类讨论是解题的关键.根据等腰三角形的定义画出图形即可.
解:如图,满足条件的等腰三角形有个,
故答案为:.
17.(1)答案见详解;(2)答案见详解.
(1)直接利用网格结合勾股定理得出符合题意的图形;
(2)直接利用网格结合勾股定理得出符合题意的图形.
(1)如图所示:即为所求;
(2)如图所示:即为所求.
18.(1)
(2)点的坐标为,点的坐标为,点的坐标
(1)利用勾股定理求出的长度,根据即可求的长;
(2)根据题意建立平面直角坐标系,根据点的坐标特征写出、、的坐标.
(1)解:,
由勾股定理得:,
,
解得:;
(2)解:平面直角坐标系如图所示,
点的坐标为,点的坐标为,点的坐标.
19.(1)见解析
(2)见解析
(1)根据正方形网格中的每个正方形边长都是1,根据勾股定理可得,边长为2的正方形的对角线长为,长为3,宽为1的长方形的对角线长为,即可得所求三角形;
(2)过表示的点B作数轴的垂线,在垂线上截取,连接,以原点为圆心,为半径画弧交数轴于点C即可.
(1)解:如图,即为所求;
根据作法得:;
(2)解:如图,点C即为所求,
理由:由作法得:,
∴,
∴点C的对应的数是.
20.(1)见解析
(2)3
(1)根据勾股定理画出图形即可.
(2)利用三角形面积公式计算即可.
(1)解:如图,即为所求;
其中,,,;
(2)如图,的面积为.
21.(1)
(2)①见解析②见解析③见解析
本题考查作图-应用与设计,三角形的面积,全等三角形的判定和性质,直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
(1)利用三角形面积公式求解即可.
(2)①根据全等三角形的判定,画出图形即可.
②利用轴对称法画出图形即可.
③画出直角三角形即可.
(1)解:的面积,
故答案为:;
(2)解:①如图,即为所画(答案不唯一)
②如图,即为所画(答案不唯一)
③如图,即为所画(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
17.1 勾股定理 第3课时 同步练习
2024--2025学年初中数学人教版版八年级下册
一、单选题
1.如图所示的网格是正方形网格,图形的各个顶点均为格点,则的度数是( )
A. B. C. D.
2.如图在的网格中,每个小正方形的边长均为2,则B到直线的距离为( )
A. B. C. D.
3.在平面直角坐标系中,点,点,x轴上取一点C使为等腰直角三角形(为斜边),则点C坐标为( )
A. B. C. D.
4.如图,在的网格中,以为一边,点在格点处,使为等腰三角形的点有( )
A.1个 B.2个 C.3个 D.4个
5.如图,已知正方形的面积为5,点A在数轴上,且表示的数为.现以点A为圆心,以的长为半径画圆,所得圆和数轴交于点E(E在A的右侧),则点E表示的数为( )
A. B. C. D.
6.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
7.如图,在中,,,,点D为AB的中点,点E为AC上一点,把沿DE折叠得到,连接.若,则的长为( )
A. B. C.4 D.
8.如图,方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,下列结论正确的有( )个;
①的形状是等腰三角形;
②的周长是;
③点C到边的距离是.
A.0个 B.1个 C.2个 D.3个
9.如图,在的正方形网格中,每个小正方形边长为1,点均为格点,以为圆心,长为半径作弧,交网格线于点,则两点间的距离为( )
A. B. C. D.
10.如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,这是边长为1的的正方形网格,的三个顶点都在格点(网格线的交点)上,则边上的高是 .
12.如图,,在数轴上点表示的数是 .
13.如图,在网格图中,小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
(1)的长为 .
(2)在中,边上的高为 .
14.在如图的网格中,每个小正方形的边长均为1,三个正方形A,B,C的面积分别用,,表示,则图中, , , .请写出、、之间的关系式: .
15.如图,中,,,,点与数轴上表示的点重合,将沿数轴正方向旋转一次使得点落在数轴上,第二次旋转使得点落在数轴上,依此类推,第2024次旋转后,落在数轴上的三角形的顶点中,右边的点表示的数是 .
16.如图,在边长为的小正方形网格中,、、、、均为格点,点是线段上的一个动点,在点运动过程中存在 个位置使得是腰长为的等腰三角形.
三、解答题
17.图①、图②都是4×4的正方形网格,每个小正方形的顶点为格点,每个小正方形的边长均为1,在图①、图②中已画出AB,点A、B均在格点上,按下列要求画图:
(1)在图①中,画一个以AB为腰且三边长都是无理数的等腰三角形ABC,点C为格点;
(2)在图②中,画一个以AB为底的等腰三角形ABD,点D为格点.
18.如图所示,的顶点、、在边长为的正方形网格的格点上,于点
(1)求的长;
(2)请在图中以为原点,边为轴建立平面直角坐标系,并写出、、的坐标.
19.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点就做格点,以格点为顶点分别按下列要求画三角形;
(1)画,使它的三边长分别为(在图中画出一个既可);
(2)请在数轴上作出的对应点(保留作图痕迹).
20.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点.
(1)以格点为顶点画,使三边长为:3,,;
(2)求的面积.
21.小正方形网格中,三个顶点均在格点上的三角形叫做格点三角形.设每个小正方形边长为1.如下图,格点,
(1)图中格点的面积是_______;
(2)按要求画图:
①在图1中画一个与全等且有一条公共边的格点三角形;
②在图2中画一个与全等且只有唯一公共点A的格点三角形;
③在图3中画一个面积为5的格点直角三角形且直角边为网格图中的斜格点线段.
参考答案
1.A
本题考查了网格与勾股定理,全等三角形的判定和性质,等腰三角形的判定和性质,掌握网格的特点,全等三角形的判定和性质是解题的关键.
根据题意可证,得到,则有,由网格的性质可得是等腰直角三角形,,由此即可求解.
解:如图所示,
∵网格是正方形网格,
∴,,,
∴,
∴,
∴,
∴,
在中,,
∴是等腰直角三角形,
∴,
∴,
故选:A .
2.D
此题考查了勾股定理,二次根式的性质,以及三角形的面积,熟练掌握勾股定理是解本题的关键.
根据小正方形的边长为1,利用勾股定理求出,由正方形面积减去三个直角三角形面积求出三角形面积,利用面积法求出边上的高即可.
解:如图,为边上的高,
,
,,
,
解得:.
故选:B.
3.C
本题主要考查了勾股定理与坐标系,根据题意正确画出图形是解题的关键.
先根据题意画出符合条件的,然后直接确定点C的坐标即可.
解:根据题意画出等腰直角(为斜边)如下,易得点C坐标为.
故选C.
4.D
本题考查了格点与勾股定理,等腰三角形,掌握等腰三角形的定义和性质是解题的关键.
根据网格的特点,勾股定理,等腰三角形的定义和性质作图即可求解.
解:如图所示,,
∵,
∴是等腰三角形,
∴点为所求点;
∵,,,
∴是等腰三角形,
∴点为所求点;
综上所述,点有4个,
故选:D .
5.A
本题主要考查实数与数轴及两点间距离,根据两点间距离及点的位置判断出点所表示的数是解题的关键.
根据正方形的边长是面积的算术平方根得,再根据勾股定理可得,再结合A点所表示的数及间距离可得点E所表示的数.
解:∵正方形的面积为5,
∴,
∴
∵点A表示的数是,且点E在点A的右侧,
∴点E表示的数为.
故选:A.
6.B
本题考查了数轴与实数及勾股定理.根据图示,可得:点A是以为圆心,以为半径的圆与数轴的交点,再根据两点间的距离的求法,求出a的值为多少即可.
解:由勾股定理得:,
∴,
∴点A是以为圆心,以为半径的圆与数轴的交点,且在左侧,
∴.
故选:B.
7.D
过点A作AF⊥DE于点F,由直角三角形的性质可得AF=1,AE=,即可求A'E,EC的长,由勾股定理可求A'C的长.
解:如图,过点A作AF⊥DE于点F,
∵AB=4,点D为AB的中点,
∴AD=2,
∵∠ADE=30°,AF⊥DE,
∴AF=1,∠FAD=60°,
∵∠BAC=105°,
∴∠FAE=45°,AF⊥DE,
∴∠AEF=45°=∠EAF,
∴AF=EF=1,
∴AE=,
∴EC=AC-AE=2,
∵把△ADE沿DE折叠得到△A'DE,
∴∠AEA'=2∠AEF=90°,A'E=AE=,
∴A'C=,
故选D.
8.B
根据勾股定理求出、、长,即可判断①和②,根据三角形面积公式即可判断③.
解:由勾股定理得:,,,
∴,
∴的形状是等腰三角形,
∴①正确;
的周长是,
∴②错误;
设C到的距离是h,
由三角形面积公式得:,
∵,
∴,
∴③错误;
故选:B.
9.B
如图:连接AE,则AE=2、AD=1,由勾股定理可求出DE,然后运用线段的和差即可解答.
解:如图:连接AE,则AE=2,AD=1
∴DE=
∴CE=CD-DE=.
故选B.
10.B
分析:根据全等三角形的判定解答即可.
详解:由图形可知:AB=,AC=3,BC=,GD=,DE=,GE=3,DI=3,EI=,所以G,I两点与点D、点E构成的三角形与△ABC全等.
故选B.
点睛:本题考查了全等三角形的判定,关键是根据SSS证明全等三角形.
11.
本题考查了勾股定理以及三角形面积等知识,设边上的高为h,由勾股定理求出的长,再由割补法求出的面积,即可解决问题.
解:设边上的高为h,
由勾股定理得:,
∵,
∴,
∴,
即边上的高为,
故答案为:.
12.
本题考查了勾股定理的应用和实数与数轴,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.利用勾股定理求得的长度,然后结合数轴求得表示的数.
解:由图形可知,,
在数轴上,点表示的数为,点在点右侧.
在数轴上点表示的数是,
故答案为:.
13. /
此题考查了勾股定理,三角形的面积公式,关键是根据三角形的面积公式列出方程.
(1)根据勾股定理即可,
(2)根据三角形的面积公式列出方程进行计算即可.
解:(1);
故答案为:
(2)设边上的高为,
,
,
故答案为:.
14. 16 9 25
本题考查了网格中的正方形与勾股定理应用,熟练掌握正方形的面积与勾股定理的光线是解题的关键.
依题意,16,,
∵在如图的网格中,每个小正方形的边长均为1,
∴根据勾股定理,得正方形C的边长为,
∴
∵16,,,
∴.
故答案为:16,9,25,.
15.
本题考查了实数与数轴的对应关系,勾股定理,解决本题的关键是熟练掌握实数与数轴的关系.根据题意的三个顶点按的顺序依次落在数轴上,每三次一个循环,一个循环中在数轴上第一个点到第三个的长为的周长,很容易求出它的周长为.因为,所以2024次旋转共经历674个循环还余2,第2024次旋转后,落在数轴上的三角形的顶点中,右边的是点C,再求解即可.
解:中,,,,
.
的周长为.
有三个顶点,
次旋转中每三次一个循环.
,
次旋转共经历674个循环还余2.
第2024次旋转后,落在数轴上的三角形的顶点中,右边的是点C,
次旋转后点C共向右移动的总长为.
第一次的起点为,
右边的点表示的数是.
故答案为:.
16.
本题主要考查等腰三角形的判定,学会分类讨论是解题的关键.根据等腰三角形的定义画出图形即可.
解:如图,满足条件的等腰三角形有个,
故答案为:.
17.(1)答案见详解;(2)答案见详解.
(1)直接利用网格结合勾股定理得出符合题意的图形;
(2)直接利用网格结合勾股定理得出符合题意的图形.
(1)如图所示:即为所求;
(2)如图所示:即为所求.
18.(1)
(2)点的坐标为,点的坐标为,点的坐标
(1)利用勾股定理求出的长度,根据即可求的长;
(2)根据题意建立平面直角坐标系,根据点的坐标特征写出、、的坐标.
(1)解:,
由勾股定理得:,
,
解得:;
(2)解:平面直角坐标系如图所示,
点的坐标为,点的坐标为,点的坐标.
19.(1)见解析
(2)见解析
(1)根据正方形网格中的每个正方形边长都是1,根据勾股定理可得,边长为2的正方形的对角线长为,长为3,宽为1的长方形的对角线长为,即可得所求三角形;
(2)过表示的点B作数轴的垂线,在垂线上截取,连接,以原点为圆心,为半径画弧交数轴于点C即可.
(1)解:如图,即为所求;
根据作法得:;
(2)解:如图,点C即为所求,
理由:由作法得:,
∴,
∴点C的对应的数是.
20.(1)见解析
(2)3
(1)根据勾股定理画出图形即可.
(2)利用三角形面积公式计算即可.
(1)解:如图,即为所求;
其中,,,;
(2)如图,的面积为.
21.(1)
(2)①见解析②见解析③见解析
本题考查作图-应用与设计,三角形的面积,全等三角形的判定和性质,直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
(1)利用三角形面积公式求解即可.
(2)①根据全等三角形的判定,画出图形即可.
②利用轴对称法画出图形即可.
③画出直角三角形即可.
(1)解:的面积,
故答案为:;
(2)解:①如图,即为所画(答案不唯一)
②如图,即为所画(答案不唯一)
③如图,即为所画(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
