28.1.1 正弦函数 教学课件(23张PPT)-2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 28.1.1 正弦函数 教学课件(23张PPT)-2024-2025学年人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 440.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
第二十八章 锐角三角函数
28.1.1 正弦函数
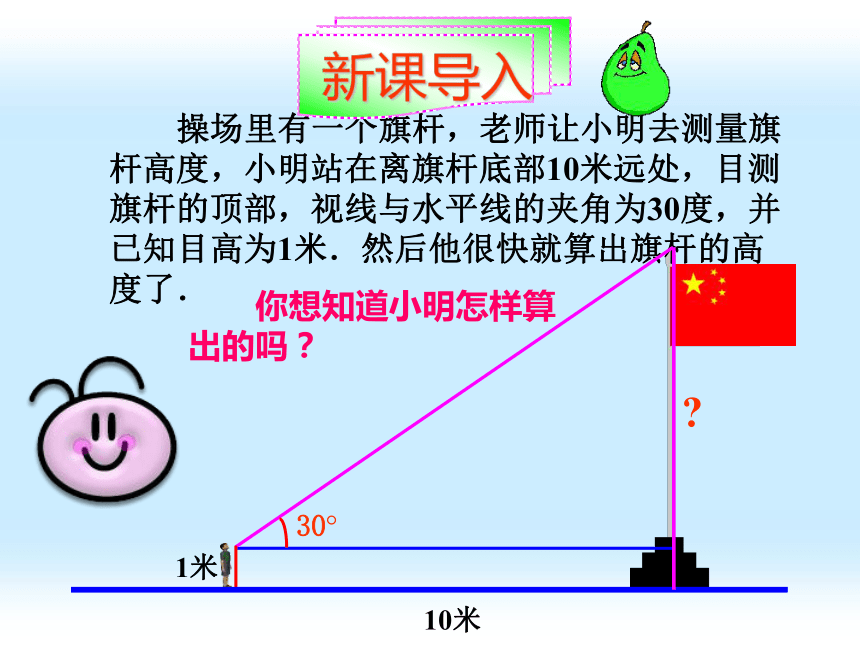
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?
新课导入
学习目标
一、课标要求:
锐角三角函数的学习要求是探索并认识锐角三角函数,能用锐角三角函数解直角三角形以及解决一些简单的实际问题等.
二、学习目标
1.经历从实际问题中抽象出数学模型的过程,探索直角三角形中边角关系的过程,体会现实生活与数学的联系;
2. 经历正弦概念的探索过程,培养自己观察分析、类比归纳的探究问题的能力。体会从特殊到一般的学习方法,进一步感受数形结合的在数学学习中的作用。
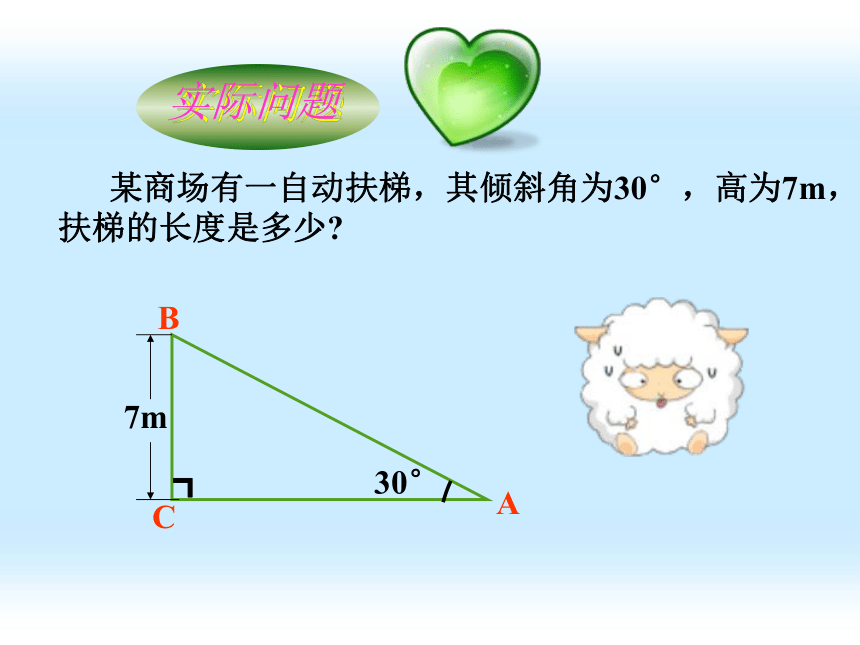
某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少
B
A
C
┓
30°
7m
实际问题
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=7m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
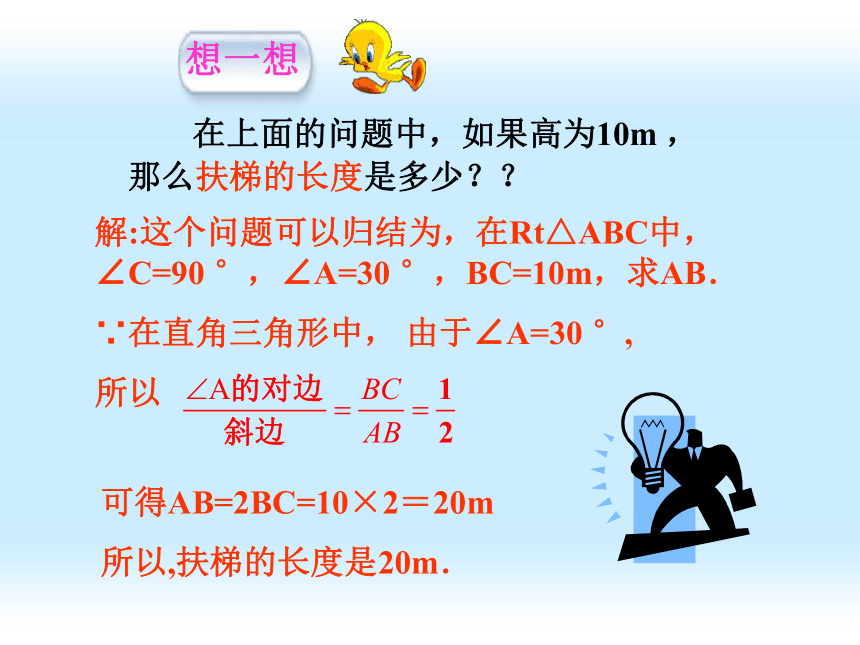
在上面的问题中,如果高为10m ,那么扶梯的长度是多少??
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=10m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
想一想
可得AB=2BC=10×2=20m
所以,扶梯的长度是20m.
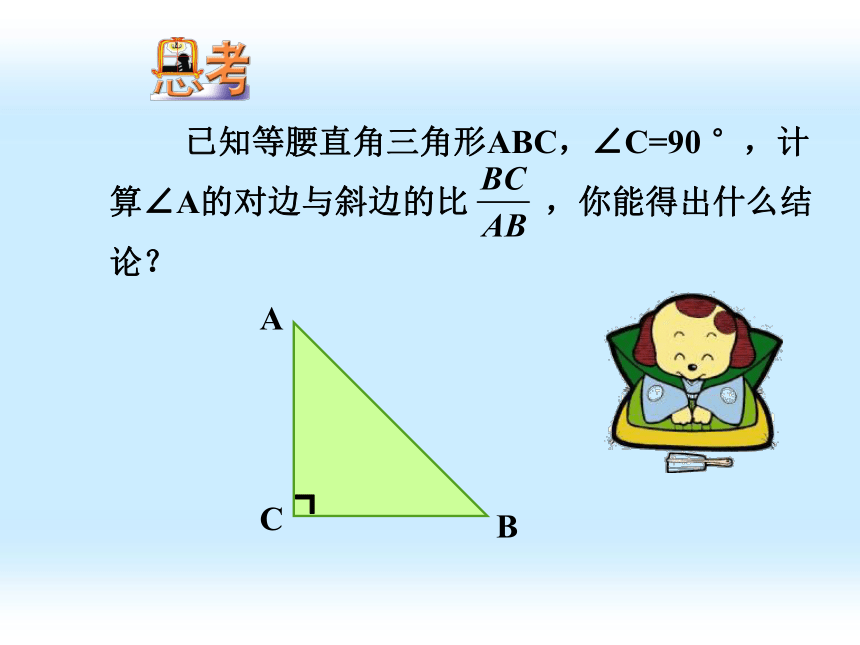
已知等腰直角三角形ABC,∠C=90 °,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
┓
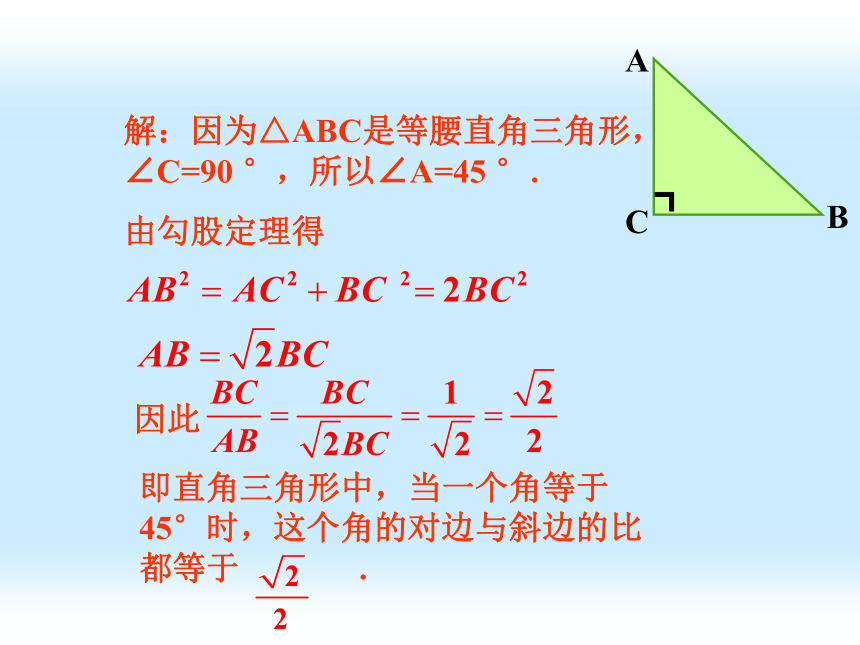
解:因为△ABC是等腰直角三角形, ∠C=90 °,所以∠A=45 °.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于 .
因此
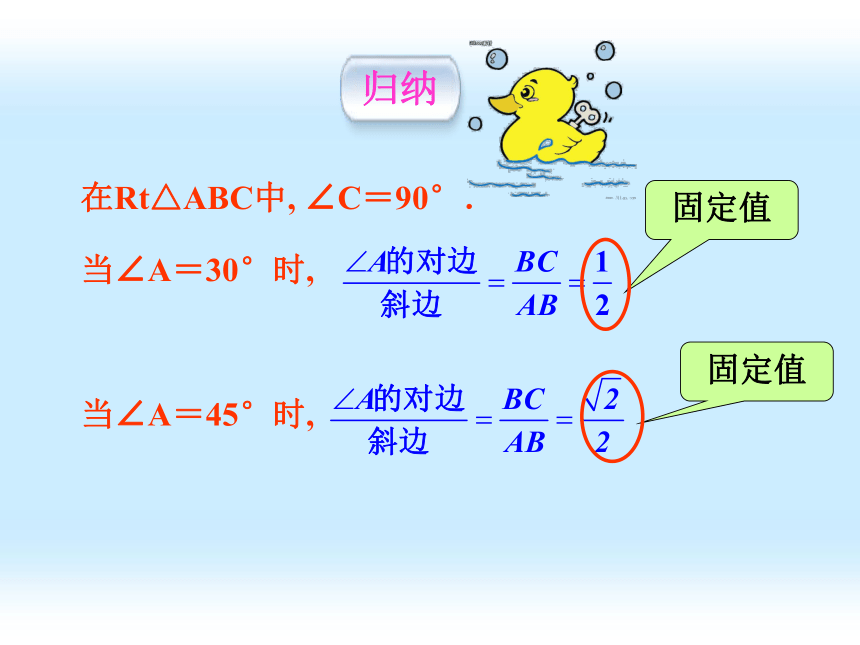
在Rt△ABC中, ∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
对于锐角A的每一个确定的值,其对边与斜边的比值也是惟一确定的 吗?
想一想
所以 =__________=__________.
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以,在Rt△ABC中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的对边与斜边的比是一个固定值.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边有什么关系?
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与斜边的比叫做∠ A的正弦(sine),记作sinA,即
一个角的正弦表示定值、比值、正值.
知识要点
正弦
正弦的表示:
(1)sinA、sin40 °、sinα(省去角的符号)
(2)sin∠ABC 、sin∠1 (不能省去角的符号)
注意:(1)sinA不是一个角 ,是一个比值
(2)sinA不是sin与A的乘积
(3)sinA没有单位
(4)∠A的正弦sinA随着∠A的变化而变化
(5)∠A的正弦sinA是∠A的对边比斜边。
知识要点
补充:直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
┓
C
A
B
斜边
c
邻边
对边
a
b
C
A
B
┓
C
A
B
【例1】如图,在Rt△ABC中, ∠C=90 °,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
6
8
(1)
(2)
A
B
C
┓
6
8
(1)
解:设如图所示,在Rt△ABC中,
因此
A
B
C
┓
(2)
解:设如图所示,在Rt△ABC中,
因此
如图,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
10
(1)
(2)
26
9
40
小练习
2.知道任意锐角A的正弦值在0~1之间,
即 0<sinA<1 (∠A为锐角).
五.课堂小结
1.“主要研究了锐角的正弦、概念,已知直角三角形的两边可求其锐角的正弦值
3、∠A的正弦sinA只与∠A的大小有关与三角形大小无关.
达标检测链接中考
达标检测:
1.在Rt△ABC中,∠C=90°,AB=3,AC=2,则sinA的值为为 .
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
3.已知在△ABC中,∠C=90°,sinA= ,BC=20,则△ABC的周长是( )
A.40 B.50 C.60 D.70
A
C
4.(2023·江苏宿迁·中考)如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则 sinB的值
达标检测链接中考
六.达标检测:
5.(2023.山东东营)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,点A,B,C,E也都在格点上,CB与⊙O相交于点D,连接ED.则∠AED的正弦值等于 .
构造解直角三角形+等角代换
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC= ,BC=2,则sin∠ACD的值为( ).
等角代换
1、完成人教版九年级下册
P64 练习1、2 P69 综合运用6
2、预习余弦、正切
第二十八章 锐角三角函数
28.1.1 正弦函数
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?
新课导入
学习目标
一、课标要求:
锐角三角函数的学习要求是探索并认识锐角三角函数,能用锐角三角函数解直角三角形以及解决一些简单的实际问题等.
二、学习目标
1.经历从实际问题中抽象出数学模型的过程,探索直角三角形中边角关系的过程,体会现实生活与数学的联系;
2. 经历正弦概念的探索过程,培养自己观察分析、类比归纳的探究问题的能力。体会从特殊到一般的学习方法,进一步感受数形结合的在数学学习中的作用。
某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少
B
A
C
┓
30°
7m
实际问题
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=7m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
在上面的问题中,如果高为10m ,那么扶梯的长度是多少??
解:这个问题可以归结为,在Rt△ABC中,∠C=90 °,∠A=30 °,BC=10m,求AB.
∵在直角三角形中, 由于∠A=30 °,
所以
想一想
可得AB=2BC=10×2=20m
所以,扶梯的长度是20m.
已知等腰直角三角形ABC,∠C=90 °,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
┓
解:因为△ABC是等腰直角三角形, ∠C=90 °,所以∠A=45 °.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于 .
因此
在Rt△ABC中, ∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
对于锐角A的每一个确定的值,其对边与斜边的比值也是惟一确定的 吗?
想一想
所以 =__________=__________.
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以,在Rt△ABC中,当锐角A的度数一定时,不管三角形的大小如何, ∠A的对边与斜边的比是一个固定值.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边有什么关系?
在Rt△ABC中, ∠C=90 °,我们把锐角A的对边与斜边的比叫做∠ A的正弦(sine),记作sinA,即
一个角的正弦表示定值、比值、正值.
知识要点
正弦
正弦的表示:
(1)sinA、sin40 °、sinα(省去角的符号)
(2)sin∠ABC 、sin∠1 (不能省去角的符号)
注意:(1)sinA不是一个角 ,是一个比值
(2)sinA不是sin与A的乘积
(3)sinA没有单位
(4)∠A的正弦sinA随着∠A的变化而变化
(5)∠A的正弦sinA是∠A的对边比斜边。
知识要点
补充:直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
┓
C
A
B
斜边
c
邻边
对边
a
b
C
A
B
┓
C
A
B
【例1】如图,在Rt△ABC中, ∠C=90 °,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
6
8
(1)
(2)
A
B
C
┓
6
8
(1)
解:设如图所示,在Rt△ABC中,
因此
A
B
C
┓
(2)
解:设如图所示,在Rt△ABC中,
因此
如图,求sinA和sinB的值.
A
B
C
A
B
C
┓
┓
10
(1)
(2)
26
9
40
小练习
2.知道任意锐角A的正弦值在0~1之间,
即 0<sinA<1 (∠A为锐角).
五.课堂小结
1.“主要研究了锐角的正弦、概念,已知直角三角形的两边可求其锐角的正弦值
3、∠A的正弦sinA只与∠A的大小有关与三角形大小无关.
达标检测链接中考
达标检测:
1.在Rt△ABC中,∠C=90°,AB=3,AC=2,则sinA的值为为 .
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
3.已知在△ABC中,∠C=90°,sinA= ,BC=20,则△ABC的周长是( )
A.40 B.50 C.60 D.70
A
C
4.(2023·江苏宿迁·中考)如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则 sinB的值
达标检测链接中考
六.达标检测:
5.(2023.山东东营)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,点A,B,C,E也都在格点上,CB与⊙O相交于点D,连接ED.则∠AED的正弦值等于 .
构造解直角三角形+等角代换
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC= ,BC=2,则sin∠ACD的值为( ).
等角代换
1、完成人教版九年级下册
P64 练习1、2 P69 综合运用6
2、预习余弦、正切
