28.1.1 正弦函数 课件(共20张PPT) 2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 28.1.1 正弦函数 课件(共20张PPT) 2024-2025学年人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
28.1.1 正弦函数
第二十八章 锐角三角函数
课前准备
课本、导学案、练习本、三角尺、铅笔
预设问题
比萨斜塔·数学问题
你能根据上述信息求出塔身中心线与垂直中心线的倾斜角吗?
C
B
A
塔身中心线
垂直中心线
┘
1972年提供的数据:
在Rt ABC中,AB=54.5m,BC=5.2m
求θ的大小
θ
学习目标
二、学习目标
1. 理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变). (重点)
2. 能根据正弦概念正确进行计算. (重点、难点)
一、课标要求:
义务教学《数学课程标准》2022年版对锐角三角函数的学习要求是探索并认识锐角三角函数,能用锐角三角函数解直角三角形以及一些解决简单的实际问题等。
温故知新
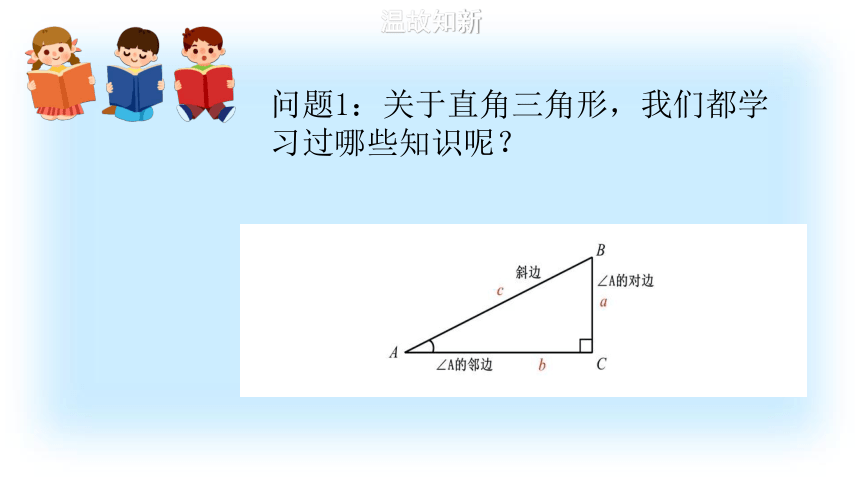
问题1:关于直角三角形,我们都学习过哪些知识呢?
新知讲授
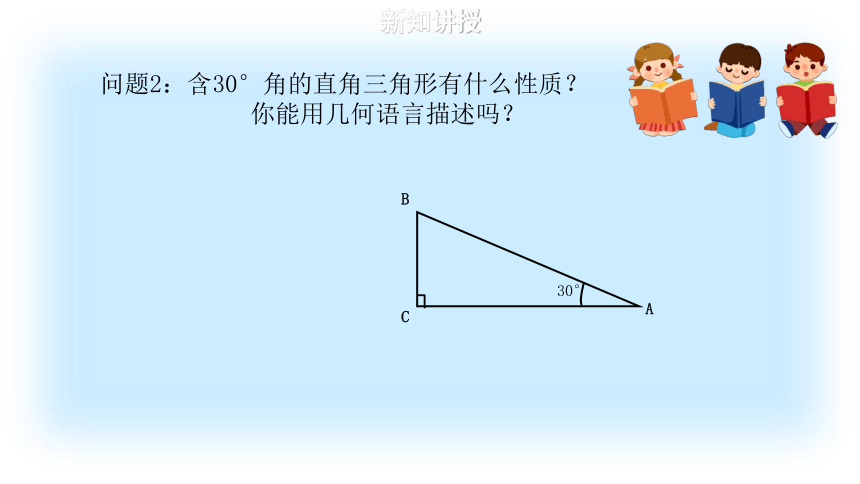
问题2:含30°角的直角三角形有什么性质?
你能用几何语言描述吗?
A
B
C
30°
┐
新知讲授
问题3:在Rt ABC中,当∠A=30°时,
我们得到∠A的对边与斜边的比值是一个定值。
请探究当∠A为其它特殊角时,对边与斜边的比值是多少?
新知讲授
思考:在Rt ABC中,当∠A是任意一个确定的锐角时,∠A的对边与斜边的比值是确定的吗?
那你能证明这一猜想吗?
A
B
C
A'
B'
C'
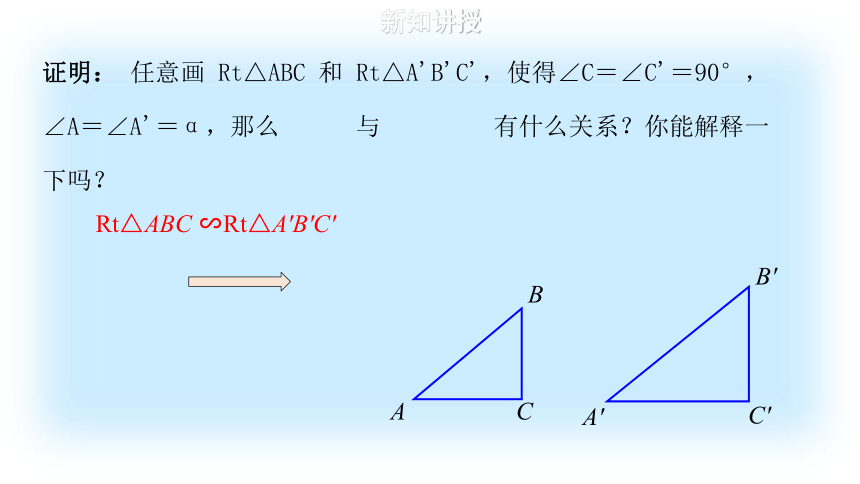
证明: 任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
新知讲授
Rt△ABC ∽Rt△A'B'C'
经过证明:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比也是一个固定值.
新知讲授
在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
归纳:
∠A的对边
斜边
sin A =
典例分析
例题1 (教材第63页例1) 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
图一:在Rt△ABC中,由勾股定理得:
AB==5
∴sinA=sinB=
图二:在Rt△ABC中,由勾股定理得:
AC==12
∴sinA=sinB=
图一
图二
典例分析
例2.如图,△ABC中,AB=AC=13,BC=10,求sinB的值。
┐
D
解:过点A作AD⊥BC,垂足为D.
∵AD=AC,BC=10,
∴BD=DC= BC=5
在Rt△ABD中,由勾股定理得,
AD==12
∴sinB==
链接中考
例3.(2023.山东东营)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,点A,B,C,E也都在格点上,CB与⊙O相交于点D,连接ED.则∠AED的正弦值等于 .
达标检测
达标检测:
1.在Rt△ABC中,∠C=90°,AB=3,AC=2,则sinA的值为为 .
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的 C.扩大为原来的3倍 D.不能确定
A
3.如图,在Rt△ABC中,∠C=90°,AB=10,
sinB= , 求AC的值.
在Rt△ABC中,∵∠C=90°,AB=10,sinB=,
∴= ∴AC=AB =10×=6
达标检测
4.如图,已知⊙O的半径为5 cm,弦AB的长为8 cm,P是AB延长线上一点,BP=2 cm,求sinP的值。
达标检测
解:作OC⊥AB于C点,根据垂径定理,AC=BC=4.∴CP=4+2=6(cm).在Rt△OAC中,OC=(cm).在Rt△OCP中,根据勾股定理得OP=(cm)
∴
课堂小结
请谈一谈本节课的收获有哪些 ?
作业布置
1、完成人教版九年级下册
P64 练习1、2 P69 综合运用6
2、预习余弦、正切
28.1.1 正弦函数
第二十八章 锐角三角函数
课前准备
课本、导学案、练习本、三角尺、铅笔
预设问题
比萨斜塔·数学问题
你能根据上述信息求出塔身中心线与垂直中心线的倾斜角吗?
C
B
A
塔身中心线
垂直中心线
┘
1972年提供的数据:
在Rt ABC中,AB=54.5m,BC=5.2m
求θ的大小
θ
学习目标
二、学习目标
1. 理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变). (重点)
2. 能根据正弦概念正确进行计算. (重点、难点)
一、课标要求:
义务教学《数学课程标准》2022年版对锐角三角函数的学习要求是探索并认识锐角三角函数,能用锐角三角函数解直角三角形以及一些解决简单的实际问题等。
温故知新
问题1:关于直角三角形,我们都学习过哪些知识呢?
新知讲授
问题2:含30°角的直角三角形有什么性质?
你能用几何语言描述吗?
A
B
C
30°
┐
新知讲授
问题3:在Rt ABC中,当∠A=30°时,
我们得到∠A的对边与斜边的比值是一个定值。
请探究当∠A为其它特殊角时,对边与斜边的比值是多少?
新知讲授
思考:在Rt ABC中,当∠A是任意一个确定的锐角时,∠A的对边与斜边的比值是确定的吗?
那你能证明这一猜想吗?
A
B
C
A'
B'
C'
证明: 任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
新知讲授
Rt△ABC ∽Rt△A'B'C'
经过证明:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比也是一个固定值.
新知讲授
在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
归纳:
∠A的对边
斜边
sin A =
典例分析
例题1 (教材第63页例1) 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
图一:在Rt△ABC中,由勾股定理得:
AB==5
∴sinA=sinB=
图二:在Rt△ABC中,由勾股定理得:
AC==12
∴sinA=sinB=
图一
图二
典例分析
例2.如图,△ABC中,AB=AC=13,BC=10,求sinB的值。
┐
D
解:过点A作AD⊥BC,垂足为D.
∵AD=AC,BC=10,
∴BD=DC= BC=5
在Rt△ABD中,由勾股定理得,
AD==12
∴sinB==
链接中考
例3.(2023.山东东营)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,点A,B,C,E也都在格点上,CB与⊙O相交于点D,连接ED.则∠AED的正弦值等于 .
达标检测
达标检测:
1.在Rt△ABC中,∠C=90°,AB=3,AC=2,则sinA的值为为 .
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的 C.扩大为原来的3倍 D.不能确定
A
3.如图,在Rt△ABC中,∠C=90°,AB=10,
sinB= , 求AC的值.
在Rt△ABC中,∵∠C=90°,AB=10,sinB=,
∴= ∴AC=AB =10×=6
达标检测
4.如图,已知⊙O的半径为5 cm,弦AB的长为8 cm,P是AB延长线上一点,BP=2 cm,求sinP的值。
达标检测
解:作OC⊥AB于C点,根据垂径定理,AC=BC=4.∴CP=4+2=6(cm).在Rt△OAC中,OC=(cm).在Rt△OCP中,根据勾股定理得OP=(cm)
∴
课堂小结
请谈一谈本节课的收获有哪些 ?
作业布置
1、完成人教版九年级下册
P64 练习1、2 P69 综合运用6
2、预习余弦、正切
