2024-2025学年河南省郑州市中原区六年级(上)调研数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省郑州市中原区六年级(上)调研数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 438.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 21:47:53 | ||
图片预览



文档简介
2024-2025学年河南省郑州市中原区六年级(上)调研数学试卷
一、口算。(0.5分×8=4分)
1.(4分)口算。
= = = =
= = = =
二、填空。(第1、4题,每题3分,其余每空2分,共16分。)
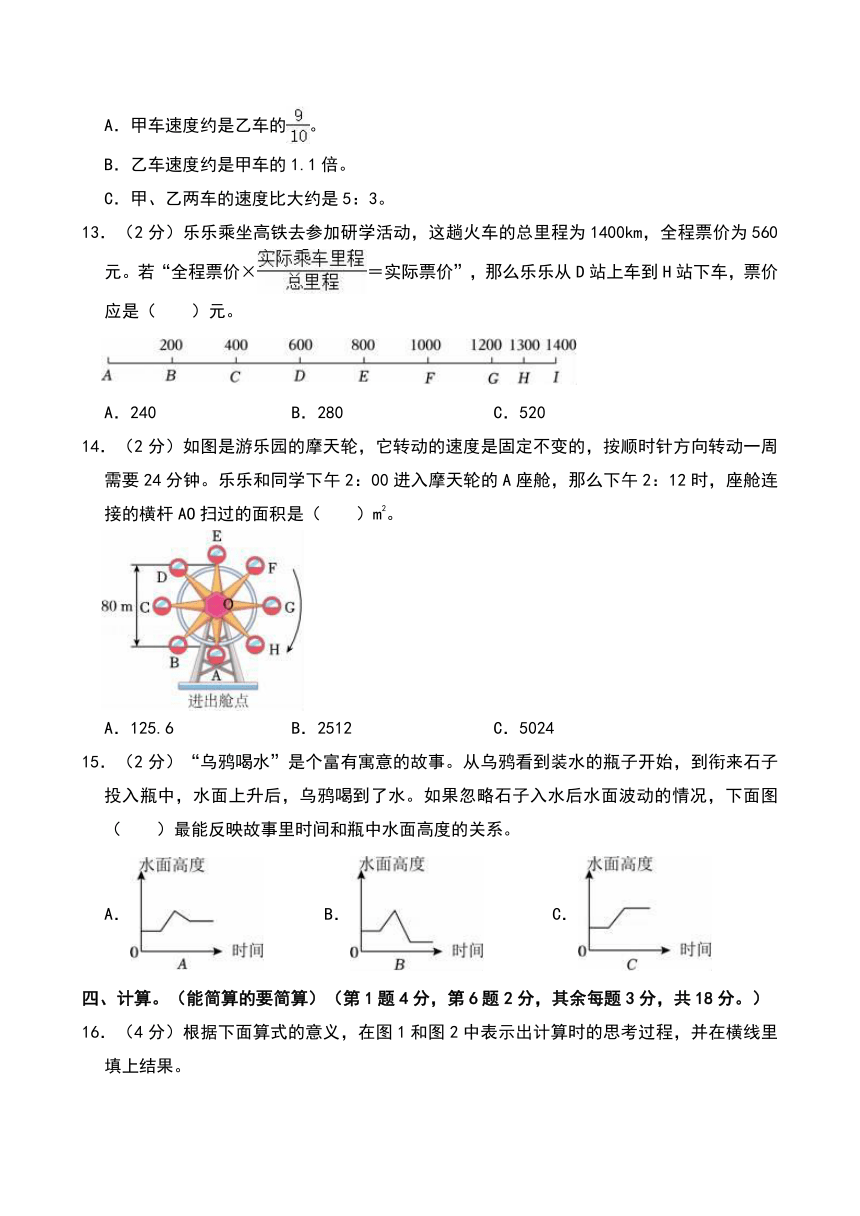
2.(3分)如图是2023年我国民用无人机市场结构及工业级无人机应用领域分布情况。
(1)工业级无人机主要用于各种专业任务和作业。由上面统计图可知,2023年巡逻巡检领域无人机数量占中国工业级无人机应用的 %。图中的17.6%表示 。
(2)2023年中国民用无人机数量达126.7万架。要求“2023年农林植保领域无人机有多少万架?”列式是 。
3.(4分)在巡逻巡检领域,传统的人力巡检是人均4千米/日,约占无人机巡检的,请根据题中给出的信息写出一个等量关系式: 。无人机巡检大约可达到人均 千米/日。
4.(2分)某医院利用医疗无人机在两个院区间运输送检标本,为患者救治争取了宝贵时间,开辟了一条“低空生命线”。原来使用救护车运输样本需要近40分钟,启用无人机后,比原来所用时间缩短了70%,缩短了 分钟。
5.(3分)利用无人机喷洒农药可以精准投放、减少污染。无人机专用药剂的稀释倍数通常为9倍:即100mL药剂加水稀释成900mL的药液。稀释后的药液中,药剂与水的比是 : 。如果配制7.2L的药液,需要药剂 L,水 L。
6.(2分)消费级无人机主要用于航拍、娱乐等休闲用途。元旦期间,某消费级无人机连续两次降价10%,乐乐认为“此时该无人机的价格比原价降低了20%”,你同意他的观点吗?请写出你的想法: 。
7.(2分)2023年我国持有无人机操控员执照的人数大约是19万人。截至到2024年7月10日,民航局公布的最新数据,目前持有无人机操控员执照的人数比去年增加了大约3.1万人,大约增加了 %。(百分号前面保留整数)
三、将正确选项对应的字母填在括号里。(2分×8=16分)
8.(2分)在探究时,同学们用不同方法表达了自己的想法,合理的是( )
A.乐乐和童童 B.乐乐和聪聪 C.童童和聪聪
9.(2分)惊蛰时节,春雷始鸣。这一天有蒙鼓皮的习俗,工匠用圆规在牛皮上画一个周长为18.84dm的圆,剪下来作为鼓皮。圆规两脚间的距离是( )dm。
A.2 B.3 C.6
10.(2分)我们常说的“百公里油耗”,指的是汽车每行驶100km所消耗汽油的升数。现在有一辆汽车行驶,消耗了汽油,这辆汽车平均每千米油耗是 L,百公里油耗是 L。
A. B. C.6
11.(2分)运输圆柱形水管时,为了防止水管滚落,会将水管捆在一起(如图)。圆柱形水管直径为a米,将两个水管捆在一起,捆一圈至少需要( )米的绳子。
A.3.14a B.4.14a C.5.14a
12.(2分)如图记录的是乙车的超车影像,则甲、乙两车速度之间的关系不可能是( )
A.甲车速度约是乙车的。
B.乙车速度约是甲车的1.1倍。
C.甲、乙两车的速度比大约是5:3。
13.(2分)乐乐乘坐高铁去参加研学活动,这趟火车的总里程为1400km,全程票价为560元。若“全程票价×=实际票价”,那么乐乐从D站上车到H站下车,票价应是( )元。
A.240 B.280 C.520
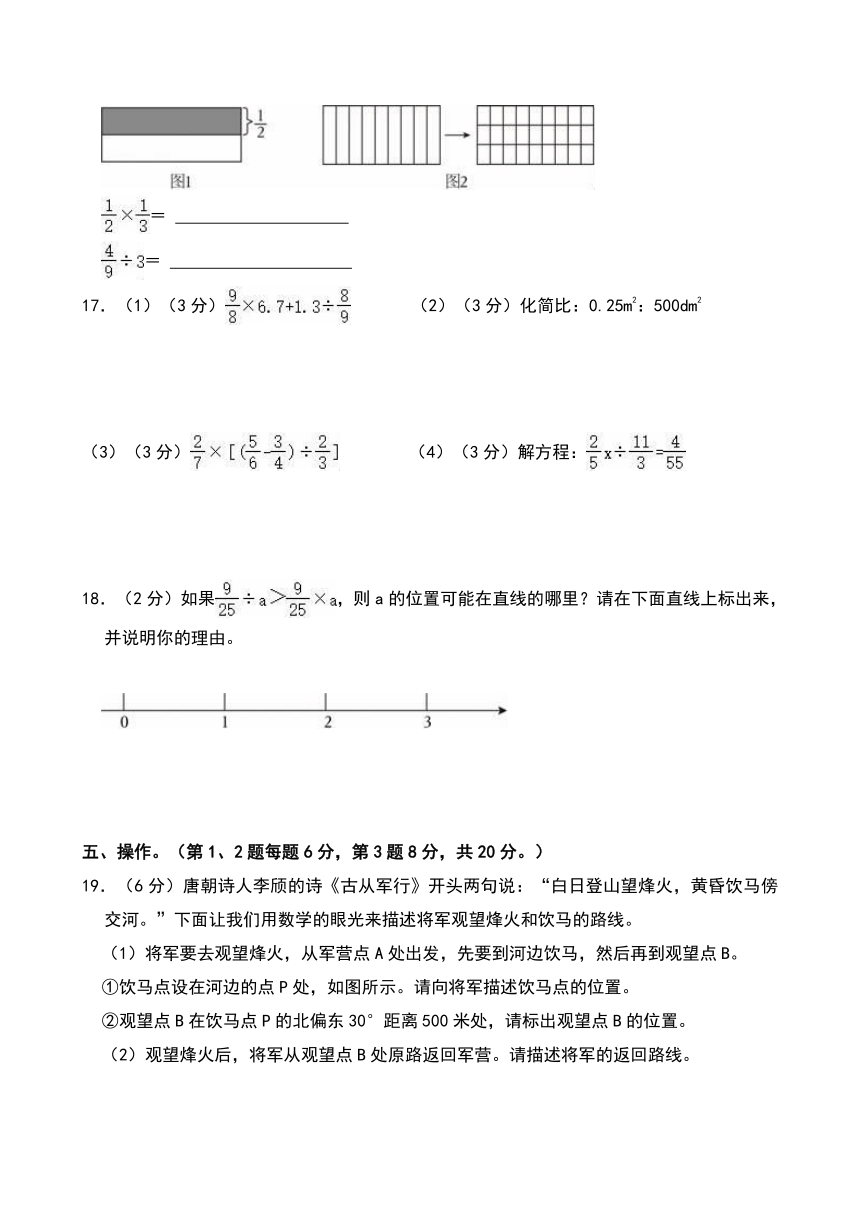
14.(2分)如图是游乐园的摩天轮,它转动的速度是固定不变的,按顺时针方向转动一周需要24分钟。乐乐和同学下午2:00进入摩天轮的A座舱,那么下午2:12时,座舱连接的横杆AO扫过的面积是( )m2。
A.125.6 B.2512 C.5024
15.(2分)“乌鸦喝水”是个富有寓意的故事。从乌鸦看到装水的瓶子开始,到衔来石子投入瓶中,水面上升后,乌鸦喝到了水。如果忽略石子入水后水面波动的情况,下面图( )最能反映故事里时间和瓶中水面高度的关系。
A. B. C.
四、计算。(能简算的要简算)(第1题4分,第6题2分,其余每题3分,共18分。)
16.(4分)根据下面算式的意义,在图1和图2中表示出计算时的思考过程,并在横线里填上结果。
=
=
17.(1)(3分) (2)(3分)化简比:0.25m2:500dm2
(3)(3分) (4)(3分)解方程:
18.(2分)如果,则a的位置可能在直线的哪里?请在下面直线上标出来,并说明你的理由。
五、操作。(第1、2题每题6分,第3题8分,共20分。)
19.(6分)唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河。”下面让我们用数学的眼光来描述将军观望烽火和饮马的路线。
(1)将军要去观望烽火,从军营点A处出发,先要到河边饮马,然后再到观望点B。
①饮马点设在河边的点P处,如图所示。请向将军描述饮马点的位置。
②观望点B在饮马点P的北偏东30°距离500米处,请标出观望点B的位置。
(2)观望烽火后,将军从观望点B处原路返回军营。请描述将军的返回路线。
20.(6分)《九章算术》中记载了一种求圆环面积的方法:“并中外周而半之,以径乘之为积步。”意思是:圆环面积=(内圆周长+外圆周长)÷2×径,其中“径”相当于环宽。
这个计算方法让“乐学”小组的同学们联想到梯形的面积公式,下面是他们探究这种求圆环面积方法的过程。
(1)他们沿一条“径”剪开,展开后得到一个近似的等腰梯形,如图所示。
梯形的上底相当于内圆的周长,下底相当于 ,高相当于 。如果用R表示外圆半径,r表示内圆半径,因为圆环的面积等于梯形的面积,所以:
(2)经测量,外圆半径为4cm,内圆半径为3cm。这个圆环的面积是多少?
21.(8分)(1)计算如图圆形和扇形的面积。
(2)乐乐发现:圆心角是90°扇形的半径是圆半径的2倍时,它们的面积有一定关系,下面是他的推理过程,请认真分析并补充。假设:圆的半径是r,则圆心角是90°扇形的半径是2r;那么,圆的面积可以表示为πr2;圆心角是90°扇形的面积可以表示为( ×,化简后为 。
所以,当圆心角是90°扇形的半径是圆的半径的2倍时,它们的面积 。
(3)请结合“乐乐的发现”,在方格纸上画一个与左侧圆面积相等的圆心角是90°的扇形。(每个小方格的边长是1cm)
六、解决问题。(第1题5分,第3题9分,其余每题4分,共26分。)
22.(5分)在河南嵩山北郊的双槐树遗址发现了我国已知最早的宫殿一河洛古国,距今已有5300多年。该遗址占地近似于一个长方形,东西长约1500米,南北长比东西长短,该遗址南北长多少米?
请先把线段图补充完整,再解答。
东西长
南北长
解答过程:
23.(4分)位于嵩山西北部的二里头遗址,被认为是夏都和夏文化的代表。三千多年前的二里头就有着先进的铸铜技术,铸铜原料主要用到铅、锡、铜,铜器种类不同原料配比也不同。一个重0.84kg的青铜盉,三种原料各需多少千克?
铜器 铅:锡:铜
笄(束发用的簪子) 6:2:975
刀 1:10:53
盉(盛酒的容器) 3:2:9
24.(9分)商朝殷墟位于河南,是中国历史上第一个既有文献记载又有考古印证的都城。
(1)商王朝拥有着强大的生产力,商王王后妇好的墓中就出土了极为丰富的随葬品。请从表中选择合适的信息,并提出一个数学问题解答。
我选的信息是: ;(填序号)
所提问题是:
解答过程:
(2)商王朝还创造了中国已知最早的成熟文字系统——甲骨文。聪聪和乐乐对甲骨文非常感兴趣,他们准备仿制卜甲上的卜辞刻写甲骨文。刻写完4片卜辞龟甲,聪聪单独刻写需要8小时,乐乐单独刻写需要12小时。如果两人合作刻写这4片卜辞龟甲,需要多少小时刻写完?
25.(4分)早在东汉时期,河南洛阳就已经有了牡丹的栽培。工匠制作的牡丹工艺品栩栩如生,现在要为它制作一个外包装框,并在工艺品和包装框之间的表面粘上金色卡纸,如图。至少需要多少平方分米的金色卡纸?
26.(4分)河南的发展在宋朝达到顶峰。北宋汝窑以青瓷闻名,因汝窑烧制工艺复杂,受到温度等因素的影响,导致出窑率不高,一般只有18%~32%。一次烧制瓷器时,共入窑200件,而珍品级瓷器的件数仅占出窑瓷器的。本次烧制的珍品级瓷器最多有多少件?
参考答案
一、口算。(0.5分×8=4分)
1.解:=6 = = =
=8.8 =0.2 =0.5 =
二、填空。(第1、4题,每题3分,其余每空2分,共16分。)
2.解:(1)1﹣17.6%﹣6%﹣37.4%﹣30%
=82.4%﹣6%﹣37.4%﹣30%
=76.4%﹣37.4%﹣30%
=39%﹣30%
=9%
因此,2023年巡逻巡检领域无人机数量占中国工业级无人机应用的9%;
图中的17.6%表示快递物流领域无人机数量占中国工业级无人机应用的17.6%;
(2)要求“2023年农林植保领域无人机有多少万架?”列式是126.7×31.3%×37.4%。
故答案为:(1)9;快递物流领域无人机数量占中国工业级无人机应用的17.6%;(2)126.7×31.3%×37.4%。
3.解:根据题中给出的信息写出一个等量关系式:无人机巡检×=人力巡检
4÷=16(千米/日)
答:根据题中给出的信息写出一个等量关系式:无人机巡检×=人力巡检。无人机巡检大约可达到人均16千米/日。
故答案为:无人机巡检×=人力巡检,16。
4.解:40×70%=28(分钟)
答:缩短了28分钟。
故答案为:28。
5.解:100:(900﹣100)=1:8
7.2×=0.8(L)
0.8×8=6.4(L)
答:药剂与水的比是18:。如果配制7.2L的药液,需要药剂0.8L,水6.4L。
故答案为:1,8,0.8,6.4。
6.解:1﹣(1﹣10%)×(1﹣10%)
=1﹣90%×90%
=1﹣81%
=19%
答:不同意,因为此时该无人机的价格比原价降低了19%。
故答案为:不同意,因为此时该无人机的价格比原价降低了19%。
7.解:3.1÷19≈16%
答:大约增加了16%。
故答案为:16。
三、将正确选项对应的字母填在括号里。(2分×8=16分)
8.解:乐乐:根据商不变的性质,被除数和除数同时乘4,商不变,所以2÷=(2×4)÷(×4),想法合理;
童童:根据商不变的性质,被除数和除数同时乘,商不变,所以2÷=(2×)÷(×),想法合理;
聪聪:根据除法的性质可得:2÷=2÷(3÷4)=2÷3×4,原题连续除以3与4,所以想法不合理。
在探究时,同学们用不同方法表达了自己的想法,合理的是乐乐和童童。
故选:A。
9.解:18.84÷3.14÷2=3(厘米)
答:圆规两脚之间的距离应是3厘米.
故选:B。
10.解:
=
=(L)
×100=6(L)
答:这辆汽车平均每千米油耗是L,百公里油耗是6L。
故答案为:A,C。
11.解:aπ+2a=(3.14+2)a=5.14a(米)
答:将两个水管捆在一起,捆一圈至少需要5.14a米的绳子。
故选:C。
12.解:图示记录的是乙车的超车影像,即乙车的速度比甲车的速度快,所以甲、乙两车的速度比不可能是5:3,即C选项说法错误。
故选:C。
13.解:1300﹣600=700(千米)
700÷1400=
560×=280(元)
答:乐乐从D站上车到H站下车,票价应是280元。
故选:B。
14.解:2时12分=2时=12分
12÷24=(圈)
×3.14×()2
=1.57×1600
=2512(平方米)
答:座舱连接的横杆AO扫过的面积是2512m2。
故选:B。
15.解:乌鸦刚衔来石子投入瓶中时,水面高度变化不大,当衔来石子越来越多时,水面开始升高,当乌鸦能接触到水面时,乌鸦开始喝水,水面开始下降,下降后的高度高于原始水面的高度。
故选:A。
四、计算。(能简算的要简算)(第1题4分,第6题2分,其余每题3分,共18分。)
16.解:
故答案为:,。
17.(1)解:
=×6.7+1.3×
=×(6.7+1.3)
=×8
=9
(2)解:0.25m2:500dm2
=25dm2:500dm2
=(25÷25):(500÷25)
=1:20
(3)解:×[()÷]
=×[÷]
=×
=
(4)解:
x÷×=×
x=
x=
18.解:
÷a=×,因为,所以×>×a,所以>a,所以0<a<1。
理由:一个数(0除外)乘大于1的数,积大于这个数;一个数(0除外)除以小于1的数,商大于这个数。
五、操作。(第1、2题每题6分,第3题8分,共20分。)
19.解:图上1厘米代表实际距离200米,(1)①200×4=800(米),从军营点A处出发,向南偏东30°方向走800米到饮马点。
②500÷200=2.5(厘米),如图:
(2)从观望点B处出发,向南偏西30°方向走500米到饮马点,然后向北偏西30°方向走800米到军营点A处。
20.解:(1)梯形的上底相当于内圆的周长,下底相当于外圆周长,高相当于环宽。
填写如下:
(2)(2×3.14×3+2×3.14)÷2×(4﹣3)外圆周长2144
=43.96÷2×1
=21.98(cm2)
答:这个圆环的面积是21.98cm2。
故答案为:外圆周长,径宽。
21.解:(1)3.14×2×2=12.56(平方厘米)
答:图形的面积是12.56平方厘米。
3.14×4×4×90°÷360°=12.56(平方厘米)
答:图形的面积是12.56平方厘米。
(2)假设:圆的半径是r,则圆心角是90°扇形的半径是2r;那么,圆的面积可以表示为πr2;圆心角是90°扇形的面积可以表示为(π(2r)2×),化简后为πr2。
(3)圆的半径是3厘米,则扇形的半径是:3×2=6(厘米),如图:
故答案为:π(2r)2×,πr2,相等。
六、解决问题。(第1题5分,第3题9分,其余每题4分,共26分。)
22.解:
1500×
=1500×
=780(米)
答:该遗址南北长780米。
23.解:0.84×=0.18(千克)
0.84×=0.12(千克)
0.84×=0.54(千克)
答:三种原料各需0.18千克、0.12千克、0.54千克。
24.解:(1)答案不唯一,我选择的信息是①和③。
提出的问题是:青铜器有多少件?
(755+25)÷
=780×
=468(件)
答:青铜器有468件。
(2)1÷(+)
=1÷
=1×
=4.8(小时)
答:如果两人合作刻写这4片卜辞龟甲,需要4.8小时刻写完。
故答案为:①、③,青铜器有多少件?
25.解:4×4﹣3.14×(4÷2)2
=16﹣12.56
=3.44(平方分米)
答:至少需要3.44平方分米的金色卡纸。
26.解:200×32%×
=64×
=4(件)
答:本次烧制的珍品级瓷器最多有4件。
一、口算。(0.5分×8=4分)
1.(4分)口算。
= = = =
= = = =
二、填空。(第1、4题,每题3分,其余每空2分,共16分。)
2.(3分)如图是2023年我国民用无人机市场结构及工业级无人机应用领域分布情况。
(1)工业级无人机主要用于各种专业任务和作业。由上面统计图可知,2023年巡逻巡检领域无人机数量占中国工业级无人机应用的 %。图中的17.6%表示 。
(2)2023年中国民用无人机数量达126.7万架。要求“2023年农林植保领域无人机有多少万架?”列式是 。
3.(4分)在巡逻巡检领域,传统的人力巡检是人均4千米/日,约占无人机巡检的,请根据题中给出的信息写出一个等量关系式: 。无人机巡检大约可达到人均 千米/日。
4.(2分)某医院利用医疗无人机在两个院区间运输送检标本,为患者救治争取了宝贵时间,开辟了一条“低空生命线”。原来使用救护车运输样本需要近40分钟,启用无人机后,比原来所用时间缩短了70%,缩短了 分钟。
5.(3分)利用无人机喷洒农药可以精准投放、减少污染。无人机专用药剂的稀释倍数通常为9倍:即100mL药剂加水稀释成900mL的药液。稀释后的药液中,药剂与水的比是 : 。如果配制7.2L的药液,需要药剂 L,水 L。
6.(2分)消费级无人机主要用于航拍、娱乐等休闲用途。元旦期间,某消费级无人机连续两次降价10%,乐乐认为“此时该无人机的价格比原价降低了20%”,你同意他的观点吗?请写出你的想法: 。
7.(2分)2023年我国持有无人机操控员执照的人数大约是19万人。截至到2024年7月10日,民航局公布的最新数据,目前持有无人机操控员执照的人数比去年增加了大约3.1万人,大约增加了 %。(百分号前面保留整数)
三、将正确选项对应的字母填在括号里。(2分×8=16分)
8.(2分)在探究时,同学们用不同方法表达了自己的想法,合理的是( )
A.乐乐和童童 B.乐乐和聪聪 C.童童和聪聪
9.(2分)惊蛰时节,春雷始鸣。这一天有蒙鼓皮的习俗,工匠用圆规在牛皮上画一个周长为18.84dm的圆,剪下来作为鼓皮。圆规两脚间的距离是( )dm。
A.2 B.3 C.6
10.(2分)我们常说的“百公里油耗”,指的是汽车每行驶100km所消耗汽油的升数。现在有一辆汽车行驶,消耗了汽油,这辆汽车平均每千米油耗是 L,百公里油耗是 L。
A. B. C.6
11.(2分)运输圆柱形水管时,为了防止水管滚落,会将水管捆在一起(如图)。圆柱形水管直径为a米,将两个水管捆在一起,捆一圈至少需要( )米的绳子。
A.3.14a B.4.14a C.5.14a
12.(2分)如图记录的是乙车的超车影像,则甲、乙两车速度之间的关系不可能是( )
A.甲车速度约是乙车的。
B.乙车速度约是甲车的1.1倍。
C.甲、乙两车的速度比大约是5:3。
13.(2分)乐乐乘坐高铁去参加研学活动,这趟火车的总里程为1400km,全程票价为560元。若“全程票价×=实际票价”,那么乐乐从D站上车到H站下车,票价应是( )元。
A.240 B.280 C.520
14.(2分)如图是游乐园的摩天轮,它转动的速度是固定不变的,按顺时针方向转动一周需要24分钟。乐乐和同学下午2:00进入摩天轮的A座舱,那么下午2:12时,座舱连接的横杆AO扫过的面积是( )m2。
A.125.6 B.2512 C.5024
15.(2分)“乌鸦喝水”是个富有寓意的故事。从乌鸦看到装水的瓶子开始,到衔来石子投入瓶中,水面上升后,乌鸦喝到了水。如果忽略石子入水后水面波动的情况,下面图( )最能反映故事里时间和瓶中水面高度的关系。
A. B. C.
四、计算。(能简算的要简算)(第1题4分,第6题2分,其余每题3分,共18分。)
16.(4分)根据下面算式的意义,在图1和图2中表示出计算时的思考过程,并在横线里填上结果。
=
=
17.(1)(3分) (2)(3分)化简比:0.25m2:500dm2
(3)(3分) (4)(3分)解方程:
18.(2分)如果,则a的位置可能在直线的哪里?请在下面直线上标出来,并说明你的理由。
五、操作。(第1、2题每题6分,第3题8分,共20分。)
19.(6分)唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河。”下面让我们用数学的眼光来描述将军观望烽火和饮马的路线。
(1)将军要去观望烽火,从军营点A处出发,先要到河边饮马,然后再到观望点B。
①饮马点设在河边的点P处,如图所示。请向将军描述饮马点的位置。
②观望点B在饮马点P的北偏东30°距离500米处,请标出观望点B的位置。
(2)观望烽火后,将军从观望点B处原路返回军营。请描述将军的返回路线。
20.(6分)《九章算术》中记载了一种求圆环面积的方法:“并中外周而半之,以径乘之为积步。”意思是:圆环面积=(内圆周长+外圆周长)÷2×径,其中“径”相当于环宽。
这个计算方法让“乐学”小组的同学们联想到梯形的面积公式,下面是他们探究这种求圆环面积方法的过程。
(1)他们沿一条“径”剪开,展开后得到一个近似的等腰梯形,如图所示。
梯形的上底相当于内圆的周长,下底相当于 ,高相当于 。如果用R表示外圆半径,r表示内圆半径,因为圆环的面积等于梯形的面积,所以:
(2)经测量,外圆半径为4cm,内圆半径为3cm。这个圆环的面积是多少?
21.(8分)(1)计算如图圆形和扇形的面积。
(2)乐乐发现:圆心角是90°扇形的半径是圆半径的2倍时,它们的面积有一定关系,下面是他的推理过程,请认真分析并补充。假设:圆的半径是r,则圆心角是90°扇形的半径是2r;那么,圆的面积可以表示为πr2;圆心角是90°扇形的面积可以表示为( ×,化简后为 。
所以,当圆心角是90°扇形的半径是圆的半径的2倍时,它们的面积 。
(3)请结合“乐乐的发现”,在方格纸上画一个与左侧圆面积相等的圆心角是90°的扇形。(每个小方格的边长是1cm)
六、解决问题。(第1题5分,第3题9分,其余每题4分,共26分。)
22.(5分)在河南嵩山北郊的双槐树遗址发现了我国已知最早的宫殿一河洛古国,距今已有5300多年。该遗址占地近似于一个长方形,东西长约1500米,南北长比东西长短,该遗址南北长多少米?
请先把线段图补充完整,再解答。
东西长
南北长
解答过程:
23.(4分)位于嵩山西北部的二里头遗址,被认为是夏都和夏文化的代表。三千多年前的二里头就有着先进的铸铜技术,铸铜原料主要用到铅、锡、铜,铜器种类不同原料配比也不同。一个重0.84kg的青铜盉,三种原料各需多少千克?
铜器 铅:锡:铜
笄(束发用的簪子) 6:2:975
刀 1:10:53
盉(盛酒的容器) 3:2:9
24.(9分)商朝殷墟位于河南,是中国历史上第一个既有文献记载又有考古印证的都城。
(1)商王朝拥有着强大的生产力,商王王后妇好的墓中就出土了极为丰富的随葬品。请从表中选择合适的信息,并提出一个数学问题解答。
我选的信息是: ;(填序号)
所提问题是:
解答过程:
(2)商王朝还创造了中国已知最早的成熟文字系统——甲骨文。聪聪和乐乐对甲骨文非常感兴趣,他们准备仿制卜甲上的卜辞刻写甲骨文。刻写完4片卜辞龟甲,聪聪单独刻写需要8小时,乐乐单独刻写需要12小时。如果两人合作刻写这4片卜辞龟甲,需要多少小时刻写完?
25.(4分)早在东汉时期,河南洛阳就已经有了牡丹的栽培。工匠制作的牡丹工艺品栩栩如生,现在要为它制作一个外包装框,并在工艺品和包装框之间的表面粘上金色卡纸,如图。至少需要多少平方分米的金色卡纸?
26.(4分)河南的发展在宋朝达到顶峰。北宋汝窑以青瓷闻名,因汝窑烧制工艺复杂,受到温度等因素的影响,导致出窑率不高,一般只有18%~32%。一次烧制瓷器时,共入窑200件,而珍品级瓷器的件数仅占出窑瓷器的。本次烧制的珍品级瓷器最多有多少件?
参考答案
一、口算。(0.5分×8=4分)
1.解:=6 = = =
=8.8 =0.2 =0.5 =
二、填空。(第1、4题,每题3分,其余每空2分,共16分。)
2.解:(1)1﹣17.6%﹣6%﹣37.4%﹣30%
=82.4%﹣6%﹣37.4%﹣30%
=76.4%﹣37.4%﹣30%
=39%﹣30%
=9%
因此,2023年巡逻巡检领域无人机数量占中国工业级无人机应用的9%;
图中的17.6%表示快递物流领域无人机数量占中国工业级无人机应用的17.6%;
(2)要求“2023年农林植保领域无人机有多少万架?”列式是126.7×31.3%×37.4%。
故答案为:(1)9;快递物流领域无人机数量占中国工业级无人机应用的17.6%;(2)126.7×31.3%×37.4%。
3.解:根据题中给出的信息写出一个等量关系式:无人机巡检×=人力巡检
4÷=16(千米/日)
答:根据题中给出的信息写出一个等量关系式:无人机巡检×=人力巡检。无人机巡检大约可达到人均16千米/日。
故答案为:无人机巡检×=人力巡检,16。
4.解:40×70%=28(分钟)
答:缩短了28分钟。
故答案为:28。
5.解:100:(900﹣100)=1:8
7.2×=0.8(L)
0.8×8=6.4(L)
答:药剂与水的比是18:。如果配制7.2L的药液,需要药剂0.8L,水6.4L。
故答案为:1,8,0.8,6.4。
6.解:1﹣(1﹣10%)×(1﹣10%)
=1﹣90%×90%
=1﹣81%
=19%
答:不同意,因为此时该无人机的价格比原价降低了19%。
故答案为:不同意,因为此时该无人机的价格比原价降低了19%。
7.解:3.1÷19≈16%
答:大约增加了16%。
故答案为:16。
三、将正确选项对应的字母填在括号里。(2分×8=16分)
8.解:乐乐:根据商不变的性质,被除数和除数同时乘4,商不变,所以2÷=(2×4)÷(×4),想法合理;
童童:根据商不变的性质,被除数和除数同时乘,商不变,所以2÷=(2×)÷(×),想法合理;
聪聪:根据除法的性质可得:2÷=2÷(3÷4)=2÷3×4,原题连续除以3与4,所以想法不合理。
在探究时,同学们用不同方法表达了自己的想法,合理的是乐乐和童童。
故选:A。
9.解:18.84÷3.14÷2=3(厘米)
答:圆规两脚之间的距离应是3厘米.
故选:B。
10.解:
=
=(L)
×100=6(L)
答:这辆汽车平均每千米油耗是L,百公里油耗是6L。
故答案为:A,C。
11.解:aπ+2a=(3.14+2)a=5.14a(米)
答:将两个水管捆在一起,捆一圈至少需要5.14a米的绳子。
故选:C。
12.解:图示记录的是乙车的超车影像,即乙车的速度比甲车的速度快,所以甲、乙两车的速度比不可能是5:3,即C选项说法错误。
故选:C。
13.解:1300﹣600=700(千米)
700÷1400=
560×=280(元)
答:乐乐从D站上车到H站下车,票价应是280元。
故选:B。
14.解:2时12分=2时=12分
12÷24=(圈)
×3.14×()2
=1.57×1600
=2512(平方米)
答:座舱连接的横杆AO扫过的面积是2512m2。
故选:B。
15.解:乌鸦刚衔来石子投入瓶中时,水面高度变化不大,当衔来石子越来越多时,水面开始升高,当乌鸦能接触到水面时,乌鸦开始喝水,水面开始下降,下降后的高度高于原始水面的高度。
故选:A。
四、计算。(能简算的要简算)(第1题4分,第6题2分,其余每题3分,共18分。)
16.解:
故答案为:,。
17.(1)解:
=×6.7+1.3×
=×(6.7+1.3)
=×8
=9
(2)解:0.25m2:500dm2
=25dm2:500dm2
=(25÷25):(500÷25)
=1:20
(3)解:×[()÷]
=×[÷]
=×
=
(4)解:
x÷×=×
x=
x=
18.解:
÷a=×,因为,所以×>×a,所以>a,所以0<a<1。
理由:一个数(0除外)乘大于1的数,积大于这个数;一个数(0除外)除以小于1的数,商大于这个数。
五、操作。(第1、2题每题6分,第3题8分,共20分。)
19.解:图上1厘米代表实际距离200米,(1)①200×4=800(米),从军营点A处出发,向南偏东30°方向走800米到饮马点。
②500÷200=2.5(厘米),如图:
(2)从观望点B处出发,向南偏西30°方向走500米到饮马点,然后向北偏西30°方向走800米到军营点A处。
20.解:(1)梯形的上底相当于内圆的周长,下底相当于外圆周长,高相当于环宽。
填写如下:
(2)(2×3.14×3+2×3.14)÷2×(4﹣3)外圆周长2144
=43.96÷2×1
=21.98(cm2)
答:这个圆环的面积是21.98cm2。
故答案为:外圆周长,径宽。
21.解:(1)3.14×2×2=12.56(平方厘米)
答:图形的面积是12.56平方厘米。
3.14×4×4×90°÷360°=12.56(平方厘米)
答:图形的面积是12.56平方厘米。
(2)假设:圆的半径是r,则圆心角是90°扇形的半径是2r;那么,圆的面积可以表示为πr2;圆心角是90°扇形的面积可以表示为(π(2r)2×),化简后为πr2。
(3)圆的半径是3厘米,则扇形的半径是:3×2=6(厘米),如图:
故答案为:π(2r)2×,πr2,相等。
六、解决问题。(第1题5分,第3题9分,其余每题4分,共26分。)
22.解:
1500×
=1500×
=780(米)
答:该遗址南北长780米。
23.解:0.84×=0.18(千克)
0.84×=0.12(千克)
0.84×=0.54(千克)
答:三种原料各需0.18千克、0.12千克、0.54千克。
24.解:(1)答案不唯一,我选择的信息是①和③。
提出的问题是:青铜器有多少件?
(755+25)÷
=780×
=468(件)
答:青铜器有468件。
(2)1÷(+)
=1÷
=1×
=4.8(小时)
答:如果两人合作刻写这4片卜辞龟甲,需要4.8小时刻写完。
故答案为:①、③,青铜器有多少件?
25.解:4×4﹣3.14×(4÷2)2
=16﹣12.56
=3.44(平方分米)
答:至少需要3.44平方分米的金色卡纸。
26.解:200×32%×
=64×
=4(件)
答:本次烧制的珍品级瓷器最多有4件。
同课章节目录
