福建省泉州市泉港区三川中学七年级数学上册 2.13 有理数的混合运算课件2 (新版)华东师大版
文档属性
| 名称 | 福建省泉州市泉港区三川中学七年级数学上册 2.13 有理数的混合运算课件2 (新版)华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 626.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-13 17:37:20 | ||
图片预览








文档简介
课件27张PPT。有理数的混合运算(1、2)welcomewelcomewelcomewelcome教学目标1.进一步掌握有理数的运算法则和运算律。
2.使学生能够熟练地按有理数运算顺序进行混合运算。
3.注意培养学生的运算能力。教学重点、难点重点:有理数的混合运算。
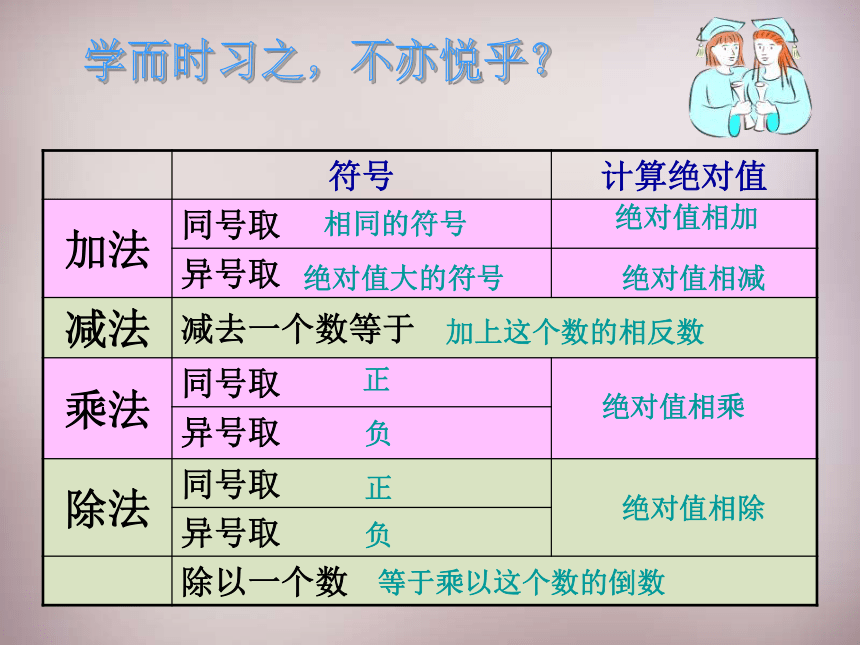
难点:准确地掌握有理数的运算顺序 和运算中的符号问题。 相同的符号
绝对值相加
负绝对值相乘
绝对值大的符号绝对值相减正
正
负绝对值相除等于乘以这个数的倒数
学而时习之,不亦悦乎?加上这个数的相反数有理数的运算学过哪些?加法
减法
乘法
除法
乘方 一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.试区别(-2)3和-23的含义与数值?解:含义: (-2)3表示-2的三次方,
-23表示2的三次方的相反数;数值:(-2)3=(-2)×(-2)×(-2)= -8,
-23 = -(2×2×2)= -8 。(-a)n和-ann为偶数时,二者数值互为相反数;
n为奇数时,二者数值相等。 一、温故知新、引入课题问:算式含有哪几种运算?
看一看,想一想,说一说第一级运算第二级运算第三级运算注:加法和减法 叫做第一级运算,乘法和除法
叫做第二级运算, 第三级运算是已学过的乘方和今后会学到的开方小括号大括号中括号1.先乘方,再乘除,最后加减;
2.同级运算,按从左到右依次进行;
3.有括号,先算小括号的,再算中括号的,最后算大括号的.二、??得出法则,揭示内涵有理数的混合运算,应按以下顺序进行:指出下列各题的运算顺序分析:有括号的先算括号里的,同级运算,按照从左到右的顺序进行.解:原式注意:在有理数乘除混合运算中,带分数一般化为假分数.三 例题示范,初步运用分析:先算乘方,再算乘除,最后算加减.
(1)
(2)除以一个数等于乘以这个数的倒数;
(3)在乘,除混合运算中先确定积的符号.解:原式(先算乘方)(化除法为乘法)(确定积的符号)(最后做加减法)(再做乘法)解:原式练一练1:指出每一步做法练一练2:22-107325四、分层练习,形成能力下课,再见作业:P65, 习题2.13第1题第二课时2.叙述有理数的运算顺序。?
3.计算:
―2.5×(―4.8)×(0.09)÷(―0.27); 温故知新、引入课题1 复习有理数的运算律:加法的交换律:
加法的结合律:
乘法的交换律:
乘法的结合律:
乘法的分配律:a+b=b+aa+(b+c)=(a+b)+cab=ba(ab)c=a(bc)a(b+c)=ab+ac分析:应按照小括号,中括号,大括号的先后顺序进行计算.解:原式例4.计算怎样才可以做得又快又准:例4.计算:解法一:原式通分化除为乘解法二:原式化除为乘乘法分配律哪种方法简单呢?
例4.计算:分析:注意到题目中的三个 , 可以逆用乘法分配律减少计算量解:原式0-3-2700能力拓展五、回顾小结,
突出重点
有理数运算技巧总结:
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式子中若既有分数又有小数,把小数 统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。下课,再见作业:P65, 习题2.13第2,3题
2.使学生能够熟练地按有理数运算顺序进行混合运算。
3.注意培养学生的运算能力。教学重点、难点重点:有理数的混合运算。
难点:准确地掌握有理数的运算顺序 和运算中的符号问题。 相同的符号
绝对值相加
负绝对值相乘
绝对值大的符号绝对值相减正
正
负绝对值相除等于乘以这个数的倒数
学而时习之,不亦悦乎?加上这个数的相反数有理数的运算学过哪些?加法
减法
乘法
除法
乘方 一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.试区别(-2)3和-23的含义与数值?解:含义: (-2)3表示-2的三次方,
-23表示2的三次方的相反数;数值:(-2)3=(-2)×(-2)×(-2)= -8,
-23 = -(2×2×2)= -8 。(-a)n和-ann为偶数时,二者数值互为相反数;
n为奇数时,二者数值相等。 一、温故知新、引入课题问:算式含有哪几种运算?
看一看,想一想,说一说第一级运算第二级运算第三级运算注:加法和减法 叫做第一级运算,乘法和除法
叫做第二级运算, 第三级运算是已学过的乘方和今后会学到的开方小括号大括号中括号1.先乘方,再乘除,最后加减;
2.同级运算,按从左到右依次进行;
3.有括号,先算小括号的,再算中括号的,最后算大括号的.二、??得出法则,揭示内涵有理数的混合运算,应按以下顺序进行:指出下列各题的运算顺序分析:有括号的先算括号里的,同级运算,按照从左到右的顺序进行.解:原式注意:在有理数乘除混合运算中,带分数一般化为假分数.三 例题示范,初步运用分析:先算乘方,再算乘除,最后算加减.
(1)
(2)除以一个数等于乘以这个数的倒数;
(3)在乘,除混合运算中先确定积的符号.解:原式(先算乘方)(化除法为乘法)(确定积的符号)(最后做加减法)(再做乘法)解:原式练一练1:指出每一步做法练一练2:22-107325四、分层练习,形成能力下课,再见作业:P65, 习题2.13第1题第二课时2.叙述有理数的运算顺序。?
3.计算:
―2.5×(―4.8)×(0.09)÷(―0.27); 温故知新、引入课题1 复习有理数的运算律:加法的交换律:
加法的结合律:
乘法的交换律:
乘法的结合律:
乘法的分配律:a+b=b+aa+(b+c)=(a+b)+cab=ba(ab)c=a(bc)a(b+c)=ab+ac分析:应按照小括号,中括号,大括号的先后顺序进行计算.解:原式例4.计算怎样才可以做得又快又准:例4.计算:解法一:原式通分化除为乘解法二:原式化除为乘乘法分配律哪种方法简单呢?
例4.计算:分析:注意到题目中的三个 , 可以逆用乘法分配律减少计算量解:原式0-3-2700能力拓展五、回顾小结,
突出重点
有理数运算技巧总结:
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式子中若既有分数又有小数,把小数 统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。下课,再见作业:P65, 习题2.13第2,3题
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
