2024-2025学年人教版九年级数学学科学业水平阶段性检测题(二)(无答案)
文档属性
| 名称 | 2024-2025学年人教版九年级数学学科学业水平阶段性检测题(二)(无答案) | 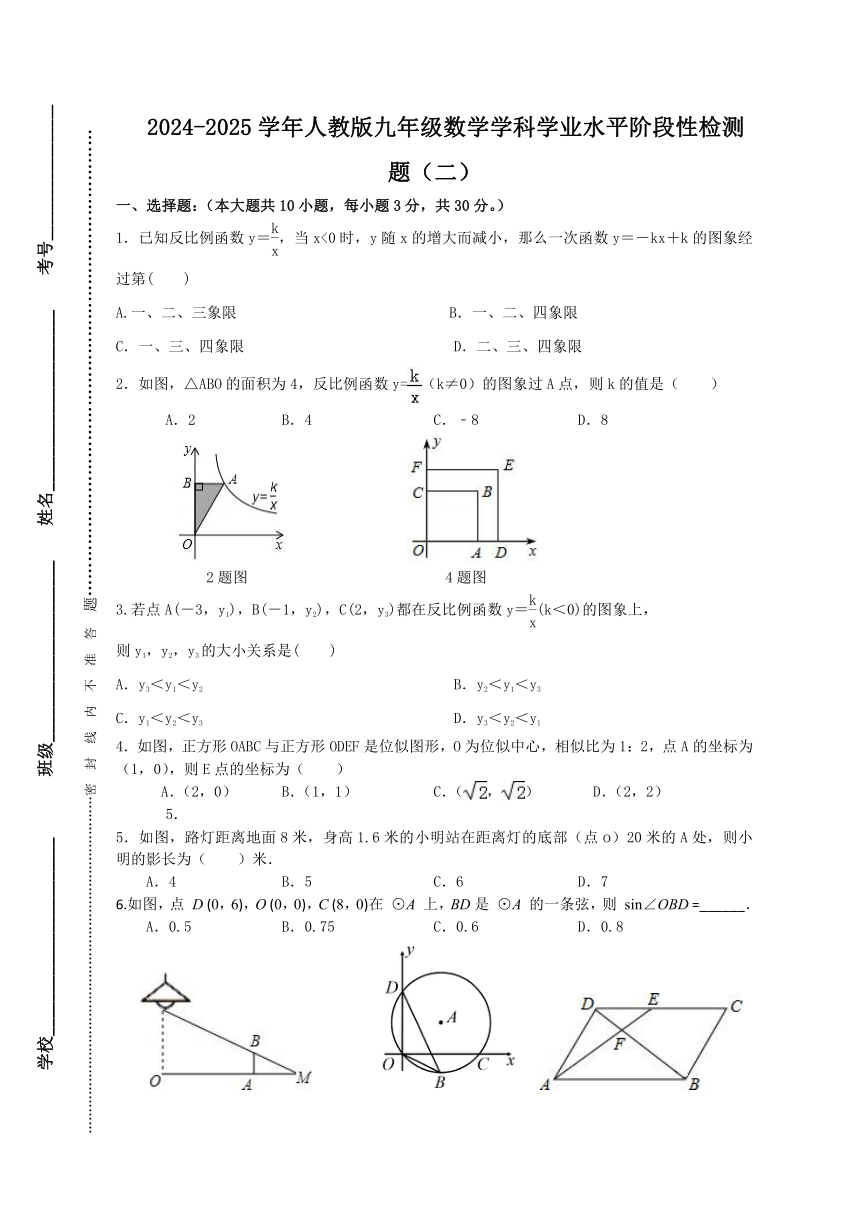 | |
| 格式 | docx | ||
| 文件大小 | 223.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 10:26:41 | ||
图片预览

文档简介
2024-2025学年人教版九年级数学学科学业水平阶段性检测题(二)
一、选择题:(本大题共10小题,每小题3分,共30分。)
1.已知反比例函数y=,当x<0时,y随x的增大而减小,那么一次函数y=-kx+k的图象经过第( )
A.一、二、三象限 B.一、二、四象限
C.一、三、四象限 D.二、三、四象限
2.如图,△ABO的面积为4,反比例函数y=(k≠0)的图象过A点,则k的值是( )
A.2 B.4 C.﹣8 D.8
2题图 4题图
3.若点A(-3,y1),B(-1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,
则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y2<y1<y3
C.y1<y2<y3 D.y3<y2<y1
4.如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:2,点A的坐标为(1,0),则E点的坐标为( )
A.(2,0) B.(1,1) C.(,) D.(2,2)
5.
5.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点o)20米的A处,则小明的影长为( )米.
A.4 B.5 C.6 D.7
6.如图,点 D (0,6),O (0,0),C (8,0)在 ⊙A 上,BD是 ⊙A 的一条弦,则 sin∠OBD =______.
A.0.5 B.0.75 C.0.6 D.0.8
5题图 6题图 7题图
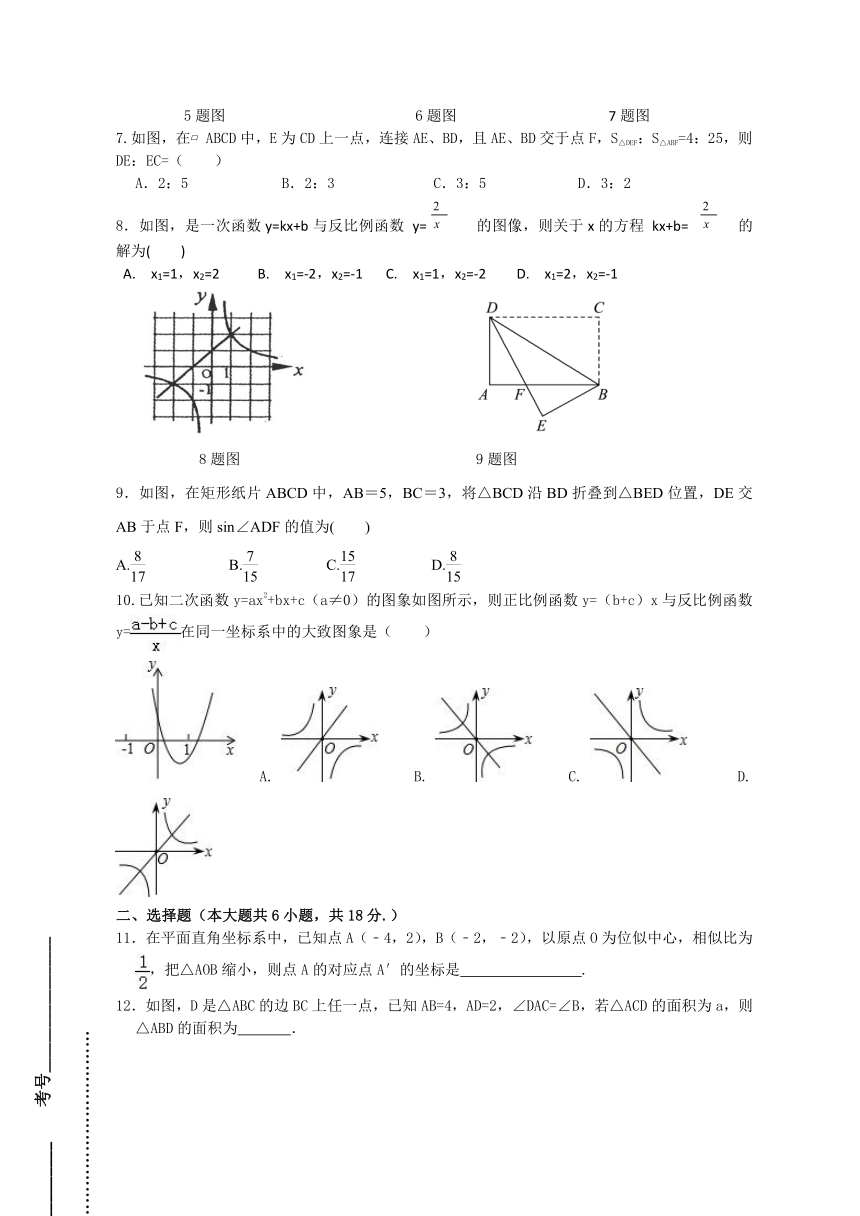
7.如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:5 B.2:3 C.3:5 D.3:2
8.如图,是一次函数y=kx+b与反比例函数 y= 的图像,则关于x的方程 kx+b= 的解为( )
A. x1=1,x2=2 B. x1=-2,x2=-1 C. x1=1,x2=-2 D. x1=2,x2=-1
8题图 9题图
9.如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则sin∠ADF的值为( )
A. B. C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=在同一坐标系中的大致图象是( )
A. B. C. D.
二、选择题(本大题共6小题,共18分.)
11.在平面直角坐标系中,已知点A(﹣4,2),B(﹣2,﹣2),以原点O为位似中心,相似比为,把△AOB缩小,则点A的对应点A′的坐标是 .
12.如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ACD的面积为a,则△ABD的面积为 .
12题图 13题图
13.如图,在网格中,小正方形的边长均为 1,点 A,B,C 都在格点上,则∠ABC 的正弦值是____.
14.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________.
15.如图,菱形ABOC在平面直角坐标系中,边OB在x轴的负半轴上,点C在反比例函数y=(k≠0)的图象上.若AB=2,∠A=60°,则反比例函数的解析式为________.
14题图 15题图 16题图
16.如图,直线l⊥x轴于点P,且与反比例函数及的图象分别交于A、B两点,连接OA、OB,已知△OAB的面积为4,则k1k2=________.
三、解答题:(本大题共7小题,共72分)
17.(6分)已知反比例函数的图象的一支如图所示,它经过点.
17题图 18题图
(1)求这个反比例函数的表达式,并补画该函数图象的另一支.
(2)求当,且时自变量x的取值范围.
18.(8分)如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使
BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长.
19.(10分)如图,AB是⊙O的直径,AM和BN是它的两条切线,过⊙O上一点E作直线DC,分别交AM,BN于点D,C,且DA=DE.求证:
(1)直线CD是⊙O的切线;
(2)OA2=DE·CE.
19题图 20题图 21题图
20.(12分)如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)求三角形CDE的面积;
(3)直接写出不等式kx+b≤的解集.
21.(12分)为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5 mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) 3 5 6 9 …
硫化物的浓度y(mg/L) 4.5 2.7 2.25 1.5 …
(1)在整改过程中,当0≤x<3时,求硫化物的浓度y与时间x的函数解析式;
(2)在整改过程中,当x≥3时,求硫化物的浓度y与时间x的函数解析式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0 mg/L?为什么?
22.(12分)如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作⊙O的切线与AC的延长线交于点P.
(1)求证:DP∥BC;
(2)求证:△ABD∽△DCP;
(3)当AB=5 cm,AC=12 cm时,求线段PC的长.
22题图 23题图
23.(12分)如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为D.
(1)求抛物线的解析式;
(2)若M是抛物线上位于线段BC上方的一个动点,求△BCM的面积的最大值;
(3)点P是对称轴左侧抛物线上的一个动点,点Q在射线ED上,若以点P,Q,E为顶点的三角形与△BOC相似,请直接写出点P的坐标.
一、选择题:(本大题共10小题,每小题3分,共30分。)
1.已知反比例函数y=,当x<0时,y随x的增大而减小,那么一次函数y=-kx+k的图象经过第( )
A.一、二、三象限 B.一、二、四象限
C.一、三、四象限 D.二、三、四象限
2.如图,△ABO的面积为4,反比例函数y=(k≠0)的图象过A点,则k的值是( )
A.2 B.4 C.﹣8 D.8
2题图 4题图
3.若点A(-3,y1),B(-1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,
则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y2<y1<y3
C.y1<y2<y3 D.y3<y2<y1
4.如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:2,点A的坐标为(1,0),则E点的坐标为( )
A.(2,0) B.(1,1) C.(,) D.(2,2)
5.
5.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点o)20米的A处,则小明的影长为( )米.
A.4 B.5 C.6 D.7
6.如图,点 D (0,6),O (0,0),C (8,0)在 ⊙A 上,BD是 ⊙A 的一条弦,则 sin∠OBD =______.
A.0.5 B.0.75 C.0.6 D.0.8
5题图 6题图 7题图
7.如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:5 B.2:3 C.3:5 D.3:2
8.如图,是一次函数y=kx+b与反比例函数 y= 的图像,则关于x的方程 kx+b= 的解为( )
A. x1=1,x2=2 B. x1=-2,x2=-1 C. x1=1,x2=-2 D. x1=2,x2=-1
8题图 9题图
9.如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则sin∠ADF的值为( )
A. B. C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=在同一坐标系中的大致图象是( )
A. B. C. D.
二、选择题(本大题共6小题,共18分.)
11.在平面直角坐标系中,已知点A(﹣4,2),B(﹣2,﹣2),以原点O为位似中心,相似比为,把△AOB缩小,则点A的对应点A′的坐标是 .
12.如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ACD的面积为a,则△ABD的面积为 .
12题图 13题图
13.如图,在网格中,小正方形的边长均为 1,点 A,B,C 都在格点上,则∠ABC 的正弦值是____.
14.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________.
15.如图,菱形ABOC在平面直角坐标系中,边OB在x轴的负半轴上,点C在反比例函数y=(k≠0)的图象上.若AB=2,∠A=60°,则反比例函数的解析式为________.
14题图 15题图 16题图
16.如图,直线l⊥x轴于点P,且与反比例函数及的图象分别交于A、B两点,连接OA、OB,已知△OAB的面积为4,则k1k2=________.
三、解答题:(本大题共7小题,共72分)
17.(6分)已知反比例函数的图象的一支如图所示,它经过点.
17题图 18题图
(1)求这个反比例函数的表达式,并补画该函数图象的另一支.
(2)求当,且时自变量x的取值范围.
18.(8分)如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使
BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长.
19.(10分)如图,AB是⊙O的直径,AM和BN是它的两条切线,过⊙O上一点E作直线DC,分别交AM,BN于点D,C,且DA=DE.求证:
(1)直线CD是⊙O的切线;
(2)OA2=DE·CE.
19题图 20题图 21题图
20.(12分)如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)求三角形CDE的面积;
(3)直接写出不等式kx+b≤的解集.
21.(12分)为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5 mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) 3 5 6 9 …
硫化物的浓度y(mg/L) 4.5 2.7 2.25 1.5 …
(1)在整改过程中,当0≤x<3时,求硫化物的浓度y与时间x的函数解析式;
(2)在整改过程中,当x≥3时,求硫化物的浓度y与时间x的函数解析式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0 mg/L?为什么?
22.(12分)如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作⊙O的切线与AC的延长线交于点P.
(1)求证:DP∥BC;
(2)求证:△ABD∽△DCP;
(3)当AB=5 cm,AC=12 cm时,求线段PC的长.
22题图 23题图
23.(12分)如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为D.
(1)求抛物线的解析式;
(2)若M是抛物线上位于线段BC上方的一个动点,求△BCM的面积的最大值;
(3)点P是对称轴左侧抛物线上的一个动点,点Q在射线ED上,若以点P,Q,E为顶点的三角形与△BOC相似,请直接写出点P的坐标.
同课章节目录
