第九章《图形的相似》综合测试卷(含答案)
文档属性
| 名称 | 第九章《图形的相似》综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 721.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 12:51:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九章综合测试卷
时间: 60分钟 满分: 100分.
一、选择题(每小题3分,共36分)
1.已知 则 ( )
A.6 B. c.
2.在中国地理地图册上,连接上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示,飞机从台湾直飞上海的距离约为1286千米,那么飞机从台湾绕道香港再到上海的飞行距离约为 ( )
A.3858千米 B.3218千米 C.2314千米 D.1543千米
第2题图 第3题图
3.[哈尔滨中考]如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点 F为BC 边上一点,连接AF交DE 于点G,则下列结论中一定正确的是 ( )
4.如图,将△ABC的三边缩小为原来的下列说法:
①△ABC与△DEF 是位似图形
②△ABC与△DEF是相似图形
③△ABC与△DEF的周长之比为2:1
④△ABC与△DEF的面积之比为4:1.
其中正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
5.两个相似五边形,一组对应边的长分别为4 cm和6cm,若它们的面积之和为 则较大五边形的面积是 ( )
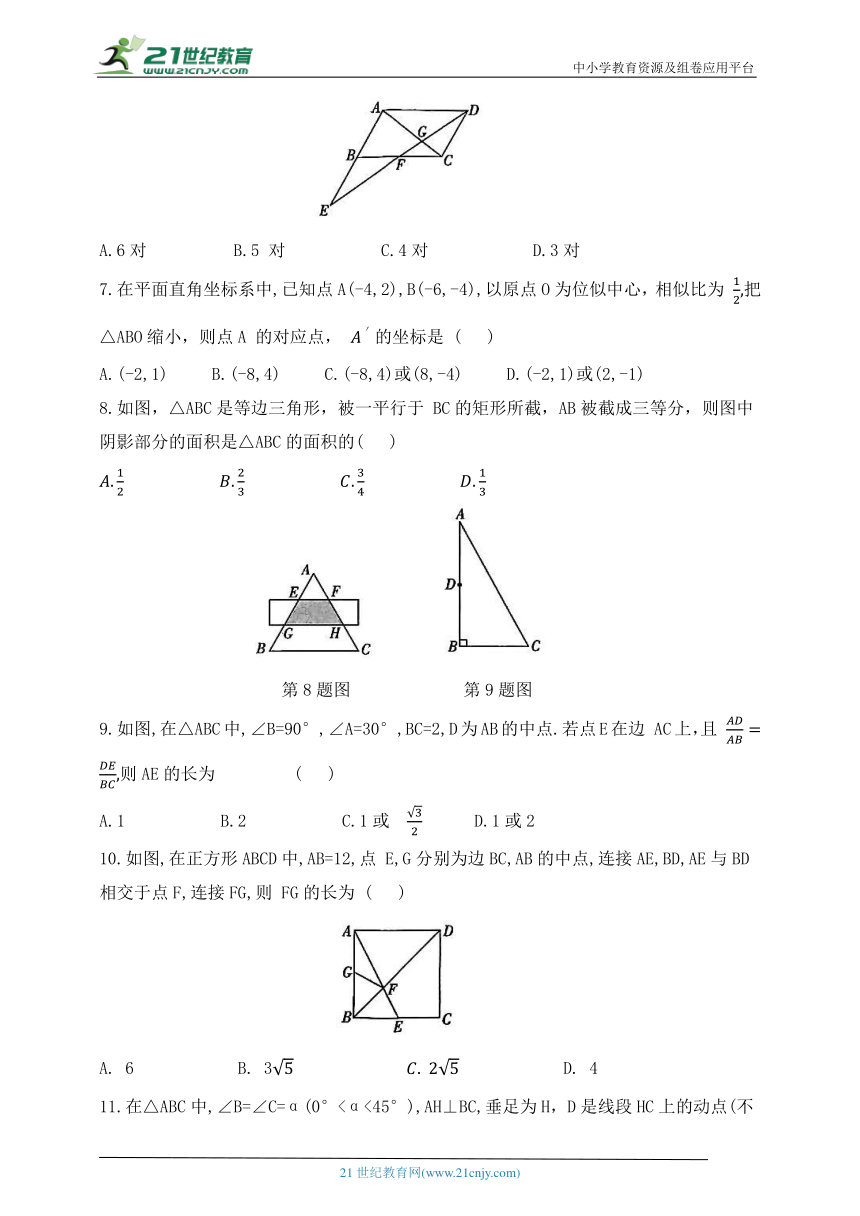
6.如图,在平行四边形ABCD中,E是AB 延长线上一点,连接DE,交AC于点G,交BC'于点F,那么图中相似三角形(不含全等三角形)共有 ( )
A.6对 B.5 对 C.4对 D.3对
7.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,相似比为 把△ABO缩小,则点A 的对应点, 的坐标是 ( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
8.如图,△ABC是等边三角形,被一平行于 BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的( )
第8题图 第9题图
9.如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边 AC上,且 则AE的长为 ( )
A.1 B.2 C.1或 D.1或2
10.如图,在正方形ABCD中,AB=12,点 E,G分别为边BC,AB的中点,连接AE,BD,AE与BD 相交于点F,连接FG,则 FG的长为 ( )
A. 6 B. 3 D. 4
11.在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点 H,C重合),将线段 DH 绕点D 顺时针旋转2a得到线段DE.两位同学经过深入研究,小明发现:当点E落在边AC 上时,点 D为HC的中点;小丽发现:连接AE,当AE的长最小时, 请对两位同学的发现作出评判 ( )
A.小明正确,小丽错误 B.小明错误,小丽正确
C.小明、小丽都正确 D.小明、小丽都错误
12.如图,在△ABC中,AB=AC=5,BC=8,D是BC 边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC 于点E,下列结论: ②1.8≤AE<5 ③当时,△ABD≌△DCE ④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共18分)
13.如果两个相似三角形对应边上的高之比是4+9,那么它们的周长之比等于 .
14.如图,在△ABC中,D,E为边AB 的三等分点,EF∥DG∥AC,H为AF与DG 的交点.若AC=6,则 .
第14题图 第15题图
15.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设. 的坐标是(3,-1),则点 B的坐标是
16.如图,在△ABC中,AD⊥BC,垂足为 D,AD=5,BC=10,四边形EFGH 和四边形HGNM 均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形 BCME 的面积比为_______.
17.如图,菱形ABCD的边长为6, 过点 D作 交BC的延长线于点E,连接AE分别交 BD,CD于点F,G,则FG的长为 .
第17题图 第18题图
18.如图,在正方形ABCD中,点E是CD 边上一点,连接BE、以BE为对角线作正方形BGEF,边 EF 与正方形ABCD 的对角线BD相交于点 H,连接AF,有以下五个结论:
①∠ABF=∠DBE ②△ABF∽△DBE ③AF⊥BD ④2BG =BH·BD ⑤若CE:DE=1:3,则
其中正确的是 .(填序号)
三、解答题(共46分)
19.(6分)(1)若 求 的值;
(2)若 且2a-b+3c=21,求a:b:c.
20.(6分)已知 在平面直角坐标系中的位置如图所示.
(1)作出 绕点C 逆时针旋转 后的
(2)以原点O为位似中心,在第四象限内作出将 缩小为原来的 后的
21.(6分)如图,在 和 中,
(1)求证:
(2)若 求 EC的长.
22.(6分)如图,小明在阳光下利用标杆AB测量校园内一棵小树CD 的高度,在同一时刻测得标杆的影长BE为2m,小树的影长落在地面上的部分DM为3m ,落在墙上的部分 MN 为 1m ,若标杆 AB 的长为1.5m,求小树的高度CD.
23.(6分)【例题呈现】化简
思路点拨:将原式的分子、分母同乘一个代数式,使得分母不含根号,实现分母有理化.
解:将分子、分母同乘 得
【类比应用】
(1)化简
(2)宽与长的比为 的矩形叫做黄金矩形.如图,已知黄金矩形的边剪掉一个以 AB 为边的正方形ABEF后,得到新的矩形CDFE.
①求 BC的长;
②通过计算说明矩形 CDFE 是否为黄金矩形.
24.(8分)如图,在菱形ABCD中,点G在边CD上,连接AG并延长交BC 的延长线于点F,连接BD交AF 于点E,连接CE.
(1)若 请直接写出 的度数;
(2)求证:
(3)若 求CF 的长.
25.(8分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF 折叠,使点 A 的对应点 P 落在边CD 上,点 B 的对应点为点G,PG交BC 于点 H.
(1)如图1,求证:
(2)如图2,当 P为CD 的中点, 时,求GH 的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
参考答案
1. B 2. A 3. C 4. D 5. B 6. B 7. D 8. D 9. D
10. C 解析:∵四边形 ABCD 是正方形,点 E,G分别为边BC,AB的中点,AB=12,
在 Rt△ABE 中,由勾股定理,得 AE =
∵AD∥BC,∴△ADF∽△EBF,∴AF=2FE,
∵FE+FA=AE=6
∵四边形ABCD 是正方形,BD 是对角线,点 E,G分别为边BC,AB的中点,
∴∠GBF=∠EBF,BG=BE,
在△GBF与△EBF中,
∴△GBF≌△EBF(SAS),
11. C
12. C 解析:①如图1,在线段DE上取点F,使AF=AE,连接AF,则∠AFE=∠AEF,
∵AB=AC,∴∠B=∠C,
∵∠ADE=∠B=α,∴∠C=∠ADE=α,
∵∠AFE=∠DAF+∠ADE,∠AEF=∠C+∠CDE,∴∠DAF=∠CDE,
∵∠ADE+∠CDE=∠B+∠BAD,∴∠CDE=∠BAD,∴∠DAF=∠BAD,
∴△ABD∽△ADF,即
∴AD =AB·AE,故①正确;
当AD⊥BC 时,由勾股定理,得 AD = ∴3≤AD<5,
即1.8≤AE<5,故②正确;
③如图2,作AH⊥BC于点 H,作点 D关于AH 的对称点D',连接D'E,
∵AB=AC=5,
∴BD=3或BD'=5,CD=5或( 1
∵∠BAD +∠B = ∠ADC = ∠ADE +∠CDE,∠ADE=∠B=α,∴∠BAD=∠CDE,
∵∠B=∠C,DC=AB,∴△ABD≌△DCE(ASA),但△ABD'与△D'CE 显然不是全等形,故③错误;
④如图3,AD⊥BC,DE⊥AC,
∴∠ADE+∠DAE=∠C+∠DAE=90°.∴∠ADE=∠C=∠B,∴BD=4x
如图4,DE⊥BC于点 D,作AH⊥BC于点 H,
∵∠ADE=∠C,∴∠ADH=∠CAH,∴△ADH∽△CAH,
即
故④正确.
13.4:9 14.1 16.1:3
解析:∵菱形 ABCD 的边长为6,∠BAD=120°,
∴AD=BC=CD=6,AD∥BC,∠BCD=120°,∴∠DCE=60°,
∵DE⊥BC,∴∠DEC=90°,
在 Rt△DCE中,∵ 30°,
∴BE=BC+CE=9,
∵AD∥BE,
在 Rt△ADE 中,
∵AD∥BE,∴△AFD∽△EFB,
∵AD∥CE,∴△AGD∽△EGC,
18.①②③④ 解析:①∵正方形 ABCD和正方形BGEF,
∴△ABD和△FBE都是等腰直角三角形,∴∠ABD=∠FBE=45°,
∴∠ABF=∠DBE,故①正确;
②∵△ABD 和△FBE 都是等腰直角三角形,
又∵∠ABF=∠DBE,∴△ABF∽△DBE,故②正确;
③∵△ABF∽△DBE,∴∠FAB=∠EDB=45°,∴AF⊥BD,故③正确;
④∵∠BEH=∠EDB=45°,∠EBH=∠DBE,∴△BEH∽△BDE,
∴2BC =BD·BH.故④正确;
⑤∵CE:DE=1:3,∴设CE=x,DE=3x,∴BC=4x,
在 Rt△BCE中,由勾股定理,得
∴BH:DH=17:15,故⑤错误.
19.解:(1)设 ∴x=3k,y=5k,z=7k,
(2)设 则a=3k-2,b=4k,c=6k-5,
∴2(3k-2)-4k+3(6k-5)=21,解得k=2,
所以a=6-2=4,b=8,c=7,所以a:b:c=4:8:7.
20.解:(1)如图所示,△A B C即为所求作;
(2)∵A(-4,2),B(-2,6),C(0,4),以原点O为位似中心,在第四象限内作出将△ABC缩小为原来的 后的△A B C ,∴A (2,-1),B (1,-3),C (0,-2),如图所示,△A B C 即为所求作.
21.证明:(1)∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,∴∠DCE=∠ACB,
又∵∠A=∠D,∴△ABC∽△DEC;
(2)∵△ABC∽△DEC;
又∵BC=6,∴CE=9.
22.解:如图,
由题意,得 即 解得
由 得 解得CD=3:25.
答:小树的高度CD为3.25 m.
23.解: 故答案为
(2)①∵四边形 ABCD 是黄金矩形(AB<BC),AB=2,
解得 ∴BC的长为
②∵四边形ABEF 是正方形,∴AB=BE=2,
∵四边形CDFE是矩形,∴CD=AB=2,
∴矩形CDFE是黄金矩形.
24.解:(1)∵四边形 ABCD是菱形,BE=BC,∴AB= BC= BE,AD∥BC,∠ABD= 70°,∴∠DAE=∠BAD-∠BAE=100°-70°=30°;
(2)证明:∵四边形ABCD 是菱形,∴DA=DC,∠ADE=∠CDE,
又∵DE=DE,∴△ADE≌△CDE(SAS),∴∠DAF=∠DCE,
又∵AD∥BC,∴∠DAF=∠F,∴∠DCE=∠F,
又∵∠CEF=∠GEC,∴△CEG∽△FEC,即EC =EF·EG;
(3)在菱形ABCD中,CD=AB=6,设GE=a,则AE=CE=3a,
∵EC =EF·EG,∴EF=9a,∴AG=AE+EG=3a+a=4a,FG=FE-EG=9a-a=8a,
又∵AD∥BC,∴∠ADG=∠DCF,∠DAF=∠F,
∴△ADG∽△FCG,∴CF=2AD=2×6=12.
25.解:(1)证明:如图1,
∵四边形 ABCD是矩形,∴∠A=∠D=∠C=90°,∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形 ABFE沿EF 翻折,使A 的对称点 P 落在DC上,
∴∠EPH=∠A=90°,∴∠1+∠2=90°,∴∠3=∠2,∴△EDP∽△PCH;
(2)∵四边形ABCD 是矩形,∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
设EP=AE=x,∴ED=AD-x=3-x,
在 Rt△EDP中,
即 解得
∵△EDP∽△PCH,即.
∵PG=AB=2,
(3)如图2,延长AB,PG交于一点 M,连接AP,
∵E,F分别在AD,BC上,将四边形 ABFE沿EF 翻折,使A 的对称点 P 落在CD上,
∴AP⊥EF,BG⊥直线EF,∴BG∥AP,
∵AE=EP,∴∠EAP=∠EPA,∴∠BAP=∠GPA,
∴△MAP 是等腰三角形,∴MA=MP,
∵P为CD 中点,∴设 DP=CP=y,∴AB=PG=CD=2y,
∵H为BC 中点,∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,∴MP=MA=MB+AB=3y,
在 Rt△PCH 中,
在 Rt△APD 中,
∵BG∥AP,∴△BMG∽△AMP,
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章综合测试卷
时间: 60分钟 满分: 100分.
一、选择题(每小题3分,共36分)
1.已知 则 ( )
A.6 B. c.
2.在中国地理地图册上,连接上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示,飞机从台湾直飞上海的距离约为1286千米,那么飞机从台湾绕道香港再到上海的飞行距离约为 ( )
A.3858千米 B.3218千米 C.2314千米 D.1543千米
第2题图 第3题图
3.[哈尔滨中考]如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点 F为BC 边上一点,连接AF交DE 于点G,则下列结论中一定正确的是 ( )
4.如图,将△ABC的三边缩小为原来的下列说法:
①△ABC与△DEF 是位似图形
②△ABC与△DEF是相似图形
③△ABC与△DEF的周长之比为2:1
④△ABC与△DEF的面积之比为4:1.
其中正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
5.两个相似五边形,一组对应边的长分别为4 cm和6cm,若它们的面积之和为 则较大五边形的面积是 ( )
6.如图,在平行四边形ABCD中,E是AB 延长线上一点,连接DE,交AC于点G,交BC'于点F,那么图中相似三角形(不含全等三角形)共有 ( )
A.6对 B.5 对 C.4对 D.3对
7.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,相似比为 把△ABO缩小,则点A 的对应点, 的坐标是 ( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
8.如图,△ABC是等边三角形,被一平行于 BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的( )
第8题图 第9题图
9.如图,在△ABC中,∠B=90°,∠A=30°,BC=2,D为AB的中点.若点E在边 AC上,且 则AE的长为 ( )
A.1 B.2 C.1或 D.1或2
10.如图,在正方形ABCD中,AB=12,点 E,G分别为边BC,AB的中点,连接AE,BD,AE与BD 相交于点F,连接FG,则 FG的长为 ( )
A. 6 B. 3 D. 4
11.在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点 H,C重合),将线段 DH 绕点D 顺时针旋转2a得到线段DE.两位同学经过深入研究,小明发现:当点E落在边AC 上时,点 D为HC的中点;小丽发现:连接AE,当AE的长最小时, 请对两位同学的发现作出评判 ( )
A.小明正确,小丽错误 B.小明错误,小丽正确
C.小明、小丽都正确 D.小明、小丽都错误
12.如图,在△ABC中,AB=AC=5,BC=8,D是BC 边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC 于点E,下列结论: ②1.8≤AE<5 ③当时,△ABD≌△DCE ④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共18分)
13.如果两个相似三角形对应边上的高之比是4+9,那么它们的周长之比等于 .
14.如图,在△ABC中,D,E为边AB 的三等分点,EF∥DG∥AC,H为AF与DG 的交点.若AC=6,则 .
第14题图 第15题图
15.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设. 的坐标是(3,-1),则点 B的坐标是
16.如图,在△ABC中,AD⊥BC,垂足为 D,AD=5,BC=10,四边形EFGH 和四边形HGNM 均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形 BCME 的面积比为_______.
17.如图,菱形ABCD的边长为6, 过点 D作 交BC的延长线于点E,连接AE分别交 BD,CD于点F,G,则FG的长为 .
第17题图 第18题图
18.如图,在正方形ABCD中,点E是CD 边上一点,连接BE、以BE为对角线作正方形BGEF,边 EF 与正方形ABCD 的对角线BD相交于点 H,连接AF,有以下五个结论:
①∠ABF=∠DBE ②△ABF∽△DBE ③AF⊥BD ④2BG =BH·BD ⑤若CE:DE=1:3,则
其中正确的是 .(填序号)
三、解答题(共46分)
19.(6分)(1)若 求 的值;
(2)若 且2a-b+3c=21,求a:b:c.
20.(6分)已知 在平面直角坐标系中的位置如图所示.
(1)作出 绕点C 逆时针旋转 后的
(2)以原点O为位似中心,在第四象限内作出将 缩小为原来的 后的
21.(6分)如图,在 和 中,
(1)求证:
(2)若 求 EC的长.
22.(6分)如图,小明在阳光下利用标杆AB测量校园内一棵小树CD 的高度,在同一时刻测得标杆的影长BE为2m,小树的影长落在地面上的部分DM为3m ,落在墙上的部分 MN 为 1m ,若标杆 AB 的长为1.5m,求小树的高度CD.
23.(6分)【例题呈现】化简
思路点拨:将原式的分子、分母同乘一个代数式,使得分母不含根号,实现分母有理化.
解:将分子、分母同乘 得
【类比应用】
(1)化简
(2)宽与长的比为 的矩形叫做黄金矩形.如图,已知黄金矩形的边剪掉一个以 AB 为边的正方形ABEF后,得到新的矩形CDFE.
①求 BC的长;
②通过计算说明矩形 CDFE 是否为黄金矩形.
24.(8分)如图,在菱形ABCD中,点G在边CD上,连接AG并延长交BC 的延长线于点F,连接BD交AF 于点E,连接CE.
(1)若 请直接写出 的度数;
(2)求证:
(3)若 求CF 的长.
25.(8分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF 折叠,使点 A 的对应点 P 落在边CD 上,点 B 的对应点为点G,PG交BC 于点 H.
(1)如图1,求证:
(2)如图2,当 P为CD 的中点, 时,求GH 的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
参考答案
1. B 2. A 3. C 4. D 5. B 6. B 7. D 8. D 9. D
10. C 解析:∵四边形 ABCD 是正方形,点 E,G分别为边BC,AB的中点,AB=12,
在 Rt△ABE 中,由勾股定理,得 AE =
∵AD∥BC,∴△ADF∽△EBF,∴AF=2FE,
∵FE+FA=AE=6
∵四边形ABCD 是正方形,BD 是对角线,点 E,G分别为边BC,AB的中点,
∴∠GBF=∠EBF,BG=BE,
在△GBF与△EBF中,
∴△GBF≌△EBF(SAS),
11. C
12. C 解析:①如图1,在线段DE上取点F,使AF=AE,连接AF,则∠AFE=∠AEF,
∵AB=AC,∴∠B=∠C,
∵∠ADE=∠B=α,∴∠C=∠ADE=α,
∵∠AFE=∠DAF+∠ADE,∠AEF=∠C+∠CDE,∴∠DAF=∠CDE,
∵∠ADE+∠CDE=∠B+∠BAD,∴∠CDE=∠BAD,∴∠DAF=∠BAD,
∴△ABD∽△ADF,即
∴AD =AB·AE,故①正确;
当AD⊥BC 时,由勾股定理,得 AD = ∴3≤AD<5,
即1.8≤AE<5,故②正确;
③如图2,作AH⊥BC于点 H,作点 D关于AH 的对称点D',连接D'E,
∵AB=AC=5,
∴BD=3或BD'=5,CD=5或( 1
∵∠BAD +∠B = ∠ADC = ∠ADE +∠CDE,∠ADE=∠B=α,∴∠BAD=∠CDE,
∵∠B=∠C,DC=AB,∴△ABD≌△DCE(ASA),但△ABD'与△D'CE 显然不是全等形,故③错误;
④如图3,AD⊥BC,DE⊥AC,
∴∠ADE+∠DAE=∠C+∠DAE=90°.∴∠ADE=∠C=∠B,∴BD=4x
如图4,DE⊥BC于点 D,作AH⊥BC于点 H,
∵∠ADE=∠C,∴∠ADH=∠CAH,∴△ADH∽△CAH,
即
故④正确.
13.4:9 14.1 16.1:3
解析:∵菱形 ABCD 的边长为6,∠BAD=120°,
∴AD=BC=CD=6,AD∥BC,∠BCD=120°,∴∠DCE=60°,
∵DE⊥BC,∴∠DEC=90°,
在 Rt△DCE中,∵ 30°,
∴BE=BC+CE=9,
∵AD∥BE,
在 Rt△ADE 中,
∵AD∥BE,∴△AFD∽△EFB,
∵AD∥CE,∴△AGD∽△EGC,
18.①②③④ 解析:①∵正方形 ABCD和正方形BGEF,
∴△ABD和△FBE都是等腰直角三角形,∴∠ABD=∠FBE=45°,
∴∠ABF=∠DBE,故①正确;
②∵△ABD 和△FBE 都是等腰直角三角形,
又∵∠ABF=∠DBE,∴△ABF∽△DBE,故②正确;
③∵△ABF∽△DBE,∴∠FAB=∠EDB=45°,∴AF⊥BD,故③正确;
④∵∠BEH=∠EDB=45°,∠EBH=∠DBE,∴△BEH∽△BDE,
∴2BC =BD·BH.故④正确;
⑤∵CE:DE=1:3,∴设CE=x,DE=3x,∴BC=4x,
在 Rt△BCE中,由勾股定理,得
∴BH:DH=17:15,故⑤错误.
19.解:(1)设 ∴x=3k,y=5k,z=7k,
(2)设 则a=3k-2,b=4k,c=6k-5,
∴2(3k-2)-4k+3(6k-5)=21,解得k=2,
所以a=6-2=4,b=8,c=7,所以a:b:c=4:8:7.
20.解:(1)如图所示,△A B C即为所求作;
(2)∵A(-4,2),B(-2,6),C(0,4),以原点O为位似中心,在第四象限内作出将△ABC缩小为原来的 后的△A B C ,∴A (2,-1),B (1,-3),C (0,-2),如图所示,△A B C 即为所求作.
21.证明:(1)∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,∴∠DCE=∠ACB,
又∵∠A=∠D,∴△ABC∽△DEC;
(2)∵△ABC∽△DEC;
又∵BC=6,∴CE=9.
22.解:如图,
由题意,得 即 解得
由 得 解得CD=3:25.
答:小树的高度CD为3.25 m.
23.解: 故答案为
(2)①∵四边形 ABCD 是黄金矩形(AB<BC),AB=2,
解得 ∴BC的长为
②∵四边形ABEF 是正方形,∴AB=BE=2,
∵四边形CDFE是矩形,∴CD=AB=2,
∴矩形CDFE是黄金矩形.
24.解:(1)∵四边形 ABCD是菱形,BE=BC,∴AB= BC= BE,AD∥BC,∠ABD= 70°,∴∠DAE=∠BAD-∠BAE=100°-70°=30°;
(2)证明:∵四边形ABCD 是菱形,∴DA=DC,∠ADE=∠CDE,
又∵DE=DE,∴△ADE≌△CDE(SAS),∴∠DAF=∠DCE,
又∵AD∥BC,∴∠DAF=∠F,∴∠DCE=∠F,
又∵∠CEF=∠GEC,∴△CEG∽△FEC,即EC =EF·EG;
(3)在菱形ABCD中,CD=AB=6,设GE=a,则AE=CE=3a,
∵EC =EF·EG,∴EF=9a,∴AG=AE+EG=3a+a=4a,FG=FE-EG=9a-a=8a,
又∵AD∥BC,∴∠ADG=∠DCF,∠DAF=∠F,
∴△ADG∽△FCG,∴CF=2AD=2×6=12.
25.解:(1)证明:如图1,
∵四边形 ABCD是矩形,∴∠A=∠D=∠C=90°,∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形 ABFE沿EF 翻折,使A 的对称点 P 落在DC上,
∴∠EPH=∠A=90°,∴∠1+∠2=90°,∴∠3=∠2,∴△EDP∽△PCH;
(2)∵四边形ABCD 是矩形,∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
设EP=AE=x,∴ED=AD-x=3-x,
在 Rt△EDP中,
即 解得
∵△EDP∽△PCH,即.
∵PG=AB=2,
(3)如图2,延长AB,PG交于一点 M,连接AP,
∵E,F分别在AD,BC上,将四边形 ABFE沿EF 翻折,使A 的对称点 P 落在CD上,
∴AP⊥EF,BG⊥直线EF,∴BG∥AP,
∵AE=EP,∴∠EAP=∠EPA,∴∠BAP=∠GPA,
∴△MAP 是等腰三角形,∴MA=MP,
∵P为CD 中点,∴设 DP=CP=y,∴AB=PG=CD=2y,
∵H为BC 中点,∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,∴MP=MA=MB+AB=3y,
在 Rt△PCH 中,
在 Rt△APD 中,
∵BG∥AP,∴△BMG∽△AMP,
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
