五四制鲁教版数学八年级下册期末综合测试卷(含答案)
文档属性
| 名称 | 五四制鲁教版数学八年级下册期末综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 618.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 12:54:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学八年级下册期末综合测试卷
时间: 120分钟 满分: 120分.
一、选择题(本题共12个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,每小题3分,共36分)
1.二次根式 中,字母x不能取的值是 ( )
A.-1 B.0 C.1 D.2
2.下列运算正确的是 ( )
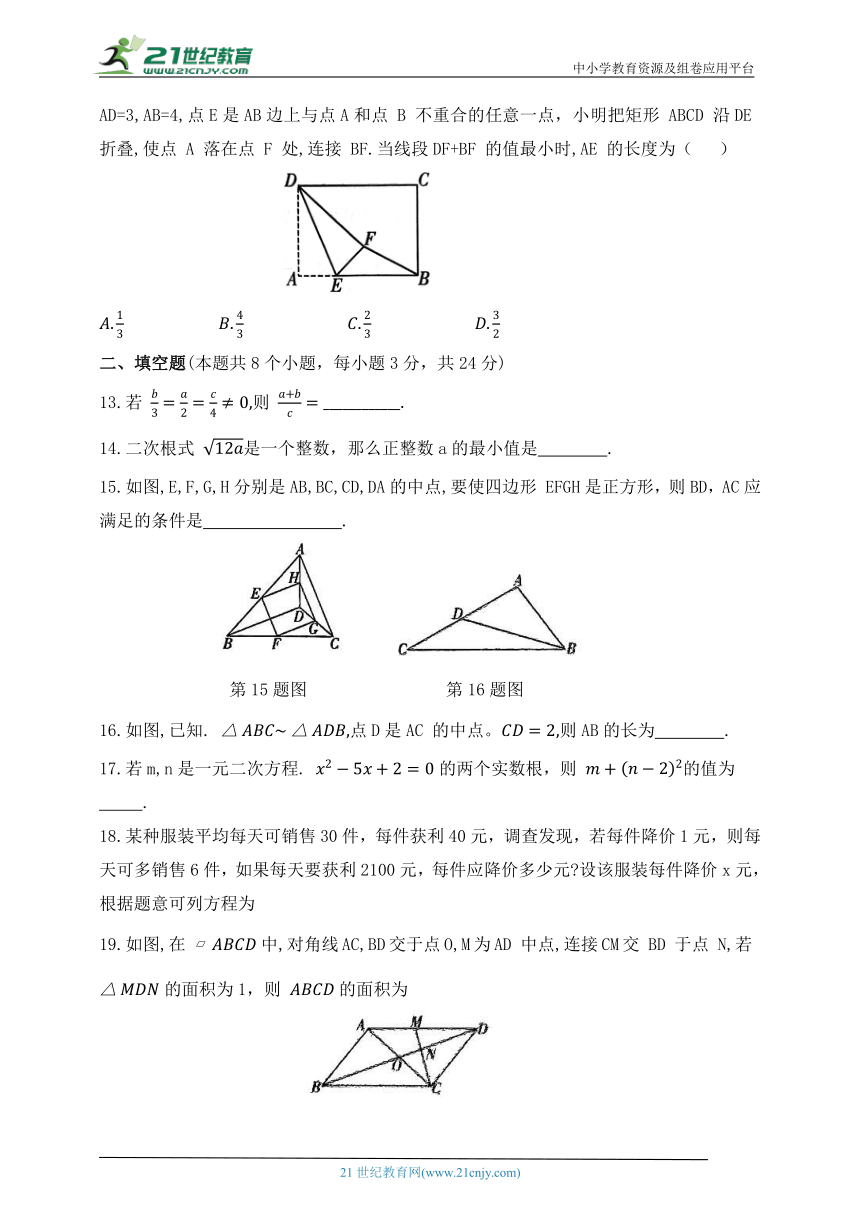
3.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m 远,该同学的身高为1.7 m,则树高为 ( )
A.3.4 m B.5.1 m C.6.8 m D.8.5 m
第3题图 第4题图
4.如图,正方形CEFG的顶点G 在正方形ABCD 的边CD上,AF与DC交于点H,若AB=6,CE=2,则DH的长为 ( )
A.2 B.3
5.已知是关于x的一元二次方程 的两个根,且则该一元二次方程是 ( )
6.已知a,b,c为常数,点 P(a,c)在第四象限,则关于x的方程 的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
7.直角三角形两条直角边长分别为 和 , 该直角三角形斜边上的中线长为 ( )
A. B. C.1 D.2
8.大自然是美的设计师,一个盆景也会产生最具美感的黄金分割比.如图,点B为AC 的黄金分割点(AB>BC),则 ( )
第8题图 第9题图
9.如图,在Rt△ABC中,根据尺规作图的痕迹,下列结论不一定正确的是( )
A. AD平分∠BAC B. DE⊥AC D. AD=CD
10.我国南宋数学家杨辉在《田亩比类乘除算法》中记录了这样一个问题:“直田积八百六十四步,只云阔与长共六十步,问阔及长各几步 ”其大意是:矩形面积是864平步,其中宽与长的和为60步,问宽和长各几步 若设长为x步,则下列符合题意的方程是 ( )
11.如图,中, 若动点E以的速度从A 点出发,在线段AB上沿着A→B→A的方向运动,设E点的运动时间为10),连接DE,当是直角三角形时,t的值为( )
A.2 B.2或7 C.2或5 D.2或5或7
12.数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,矩形ABCD中,AD=3,AB=4,点E是AB边上与点A和点 B 不重合的任意一点,小明把矩形 ABCD 沿DE 折叠,使点 A 落在点 F 处,连接 BF.当线段DF+BF 的值最小时,AE 的长度为( )
二、填空题(本题共8个小题,每小题3分,共24分)
13.若 则
14.二次根式 是一个整数,那么正整数a的最小值是 .
15.如图,E,F,G,H分别是AB,BC,CD,DA的中点,要使四边形 EFGH是正方形,则BD,AC应满足的条件是 .
第15题图 第16题图
16.如图,已知. 点D是AC 的中点。则AB的长为 .
17.若m,n是一元二次方程. 的两个实数根,则 的值为 .
18.某种服装平均每天可销售30件,每件获利40元,调查发现,若每件降价1元,则每天可多销售6件,如果每天要获利2100元,每件应降价多少元 设该服装每件降价x元,根据题意可列方程为
19.如图,在 中,对角线AC,BD交于点O,M为AD 中点,连接CM交 BD 于点 N,若 的面积为1,则 的面积为
20.问题探究;因为,所以,因为所以请你根据以上规律,结合你的经验化简下列式子:
三、解答题(本题共8个小题,要写出必要的解答过程或推理步骤,共60分)
21.(6分)计算:
.
22.(6分)解方程:
(公式法);
(配方法);
(因式分解法).
23.(6分)如图,在( 网格图中,每个小正方形边长均为1,点O和的顶点均在小正方形的顶点处.
(1)以O为位似中心,在网格图中将 C缩小到原来的 得到画出图形;
(2)连接(1)中的 求四边形 的周长(结果保留根号).
24.(6分)已知关于x的方程
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且 ,求该矩形的对角线的长.
25.(8分)综合实践活动中,某小组利用直角尺和皮尺测量建筑物AB和CD 的高,因为这两栋建筑物高度相同,于是这个小组设计出一种简捷的方案,如图所示:
(1)把直角尺的顶点E放在两栋建筑物之间的地面上,调整位置使直角尺的两边 EM,EN所在直线分别经过建筑物对立面的顶部A 和C;
(2)用皮尺度量 BE 和DE 的长度;
(3)通过计算得到建筑物的高度.若示意图中点A,B,C,D,E,M,N均在同一平面内,测得 请求出这两栋建筑的高度.
26.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元,但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
27.(10分)如图1,在矩形ABCD中,点E 为AD 边上不与端点重合的一动点,点F 是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若 求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD 是正方形, 求 的值.
28.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线;
(2)如图2,△ABC中, CD是△ABC的完美分割线,且△ACD是以CD 为底边的等腰三角形,求BD和CD 长;
(3)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,请直接写出∠ACB的度数为 .
参考答案
1. C 2. B 3. B 4. B 5. B 6. A 7. D 8. A 9. D 10. C
11. D 解析:∵∠C=90°,BC=3cm,∠B=60°,∴∠A=30°,∴AB=2BC=6 cm.
①当∠EDB=90°时,如图1,∵
∵∠C=90°,∴∠EDB=∠C,
又∵∠B=∠B,∴△BDE∽△BCA,
∴BE=4cm,则AE=6-4=2(cm),在从 A到E 的过程中,t=2,满足题意,在从 B到E 的过程中,t=6+4=10,∵,∴t=10舍去.
②当∠BED=90°时,如图2,
∵∠DEB=∠C=90°,∠B=∠B,∴△BED∽△BCA,
∴BE=1cm,∴AE=5cm,
在从A到E 的过程中,t=5,满足题意,在从B到E的过程中,t=6+1=7,满足题意.综上所述,t=2或5或7.
12. D 解析:连接BD,
∵DF+BF≥BD,当 D,F,B 共线时取等号,∴线段 DF+BF 的值最小时,点 F 在 BD上的点F'处,此时点 E在点E'处,如图,
在矩形 ABCD中,AD=3,AB=4,则 BD=
由折叠性质得
4-AE',
在Rt△E'F'B 中,由勾股定理得
解得 即线段 DF+BF的值最小时,AE的长度为 .
13. 14.3 15. AC=BD且AC⊥BD 17.7
18.(40-x)(30+6x)=2100 19.12
21.解:(1)原式
(2)原式:
)
.
22.解:
这里
∵
(2)两边都除以2,得 移项,得
配方,得 即
开平方,得 即
(3)原方程可变形为( 0.
∴(y+2+2y+1)(y+2-2y-1)=0.∴3y+3=0,1-y=0,
∴y =-1,y =1.
23.解:(1)如图,△A'B'C'即为所求作;
(2)如图, 2
∵OA=4,OC=4,
∴四边形 AA'C'C 的周长
24.解:(1)∵方程. 有两个不相等的实数根,
∴[-(2k+1)] -4×1×(k +1)=4k-3>0.
(2)当k=2时,原方程为 设方程的两个根为m,n,
∴m+n=5, mn=5,
25.解:由题意,得AB⊥BD,CD⊥BD,
∴∠BEA + ∠BAE = 90°, ∠ECD +∠DEC=90°,∠ABE=∠EDC=90°,
∵∠MEN=90°,∴∠BEA+∠DEC=90°.∴∠BAE=∠DEC.
∴△ABE∽△EDC,
设AB=CD= xm,则 解得x=18(负值舍去).
经检验,x=18是原方程的解.
答:两栋建筑物的高度为18 m.
26.解:(1)设该市参加健身运动人数的年均增长率为x,
由题意,得32(1+x) =50,解得x =0.25=25%,x =-2.25(不符合题意,舍去),
答:该市参加健身运动人数的年均增长率为25%;
(2)∵1 600×100=160 000<240 000元,∴购买的这种健身器材的套数大于100套,设购买的这种健身器材的套数为m套,
由题 意,得 240 000,
整理,得 解得
当m=300 时,售价 40=800<1000(不符合题意,故舍去),
答:购买的这种健身器材的套数为200套.
27.解:(1)证明:∵四边形 ABCD是矩形,∴∠BAD=90°,∴∠ABE+∠AEB=90°,
∵∠ABE=∠DAF,∴∠DAF+∠AEB=90°,∴∠AOE=90°,∴AF⊥BE;
(2)延长AF交CD 于点G,
∵四边形ABCD为矩形,∴AB∥CD,∠BAD=∠ADG=90°,
∴△AFB∽△GFD,
∵∠BAD = ∠ADG = 90°, ∠ABE =∠DAF,
∴△ABE∽△DAG,
(3)设正方形 ABCD 的边长为a,则AB=AD=a,延长AF交CD于点G,
∵四边形ABCD 是正方形,∴∠BAD=∠ADG=90°,AB∥CD,
∴△AFB∽△GFD,
28.解:(1)证明:∵∠A=40°,∠B=60°,
∵∠A≠∠B≠∠ACB,∴△ABC不是等腰三角形.
∵CD平分∠ACB,
∴∠ACD=∠A=40°.∴AD=CD.∴△ACD为等腰三角形.
∵∠DCB=∠A=40°.∠CBD=∠ABC,∴△BCD∽△BAC.∴CD 是△ABC的完美分割线;
(2)∵△ACD 是以CD 为底边的等腰三角形,∴AD=AC=2,∴AB=AD+BD=2+BD.
∵CD 是△ABC 的完美分割线,∴△BCD∽△BAC.
解得 或 (不合题意,舍去),
∵△BCD∽△BAC,
(3)∵CD 是△ABC 的完美分割线,且△ACD为等腰三角形,
∴①当 AC=AD 时,∠ACD=∠ADC=
∵△BCD∽△BAC,∴∠BCD=∠A=48°,
②当AD=CD时,∠A=∠ACD=48°,
∵△BCD∽△BAC,∴∠BCD=∠A=48°,
③当CD=AC时,△ABC不存在.
故答案为:96°或114°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学八年级下册期末综合测试卷
时间: 120分钟 满分: 120分.
一、选择题(本题共12个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,每小题3分,共36分)
1.二次根式 中,字母x不能取的值是 ( )
A.-1 B.0 C.1 D.2
2.下列运算正确的是 ( )
3.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m 远,该同学的身高为1.7 m,则树高为 ( )
A.3.4 m B.5.1 m C.6.8 m D.8.5 m
第3题图 第4题图
4.如图,正方形CEFG的顶点G 在正方形ABCD 的边CD上,AF与DC交于点H,若AB=6,CE=2,则DH的长为 ( )
A.2 B.3
5.已知是关于x的一元二次方程 的两个根,且则该一元二次方程是 ( )
6.已知a,b,c为常数,点 P(a,c)在第四象限,则关于x的方程 的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
7.直角三角形两条直角边长分别为 和 , 该直角三角形斜边上的中线长为 ( )
A. B. C.1 D.2
8.大自然是美的设计师,一个盆景也会产生最具美感的黄金分割比.如图,点B为AC 的黄金分割点(AB>BC),则 ( )
第8题图 第9题图
9.如图,在Rt△ABC中,根据尺规作图的痕迹,下列结论不一定正确的是( )
A. AD平分∠BAC B. DE⊥AC D. AD=CD
10.我国南宋数学家杨辉在《田亩比类乘除算法》中记录了这样一个问题:“直田积八百六十四步,只云阔与长共六十步,问阔及长各几步 ”其大意是:矩形面积是864平步,其中宽与长的和为60步,问宽和长各几步 若设长为x步,则下列符合题意的方程是 ( )
11.如图,中, 若动点E以的速度从A 点出发,在线段AB上沿着A→B→A的方向运动,设E点的运动时间为10),连接DE,当是直角三角形时,t的值为( )
A.2 B.2或7 C.2或5 D.2或5或7
12.数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,矩形ABCD中,AD=3,AB=4,点E是AB边上与点A和点 B 不重合的任意一点,小明把矩形 ABCD 沿DE 折叠,使点 A 落在点 F 处,连接 BF.当线段DF+BF 的值最小时,AE 的长度为( )
二、填空题(本题共8个小题,每小题3分,共24分)
13.若 则
14.二次根式 是一个整数,那么正整数a的最小值是 .
15.如图,E,F,G,H分别是AB,BC,CD,DA的中点,要使四边形 EFGH是正方形,则BD,AC应满足的条件是 .
第15题图 第16题图
16.如图,已知. 点D是AC 的中点。则AB的长为 .
17.若m,n是一元二次方程. 的两个实数根,则 的值为 .
18.某种服装平均每天可销售30件,每件获利40元,调查发现,若每件降价1元,则每天可多销售6件,如果每天要获利2100元,每件应降价多少元 设该服装每件降价x元,根据题意可列方程为
19.如图,在 中,对角线AC,BD交于点O,M为AD 中点,连接CM交 BD 于点 N,若 的面积为1,则 的面积为
20.问题探究;因为,所以,因为所以请你根据以上规律,结合你的经验化简下列式子:
三、解答题(本题共8个小题,要写出必要的解答过程或推理步骤,共60分)
21.(6分)计算:
.
22.(6分)解方程:
(公式法);
(配方法);
(因式分解法).
23.(6分)如图,在( 网格图中,每个小正方形边长均为1,点O和的顶点均在小正方形的顶点处.
(1)以O为位似中心,在网格图中将 C缩小到原来的 得到画出图形;
(2)连接(1)中的 求四边形 的周长(结果保留根号).
24.(6分)已知关于x的方程
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且 ,求该矩形的对角线的长.
25.(8分)综合实践活动中,某小组利用直角尺和皮尺测量建筑物AB和CD 的高,因为这两栋建筑物高度相同,于是这个小组设计出一种简捷的方案,如图所示:
(1)把直角尺的顶点E放在两栋建筑物之间的地面上,调整位置使直角尺的两边 EM,EN所在直线分别经过建筑物对立面的顶部A 和C;
(2)用皮尺度量 BE 和DE 的长度;
(3)通过计算得到建筑物的高度.若示意图中点A,B,C,D,E,M,N均在同一平面内,测得 请求出这两栋建筑的高度.
26.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元,但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
27.(10分)如图1,在矩形ABCD中,点E 为AD 边上不与端点重合的一动点,点F 是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若 求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD 是正方形, 求 的值.
28.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线;
(2)如图2,△ABC中, CD是△ABC的完美分割线,且△ACD是以CD 为底边的等腰三角形,求BD和CD 长;
(3)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,请直接写出∠ACB的度数为 .
参考答案
1. C 2. B 3. B 4. B 5. B 6. A 7. D 8. A 9. D 10. C
11. D 解析:∵∠C=90°,BC=3cm,∠B=60°,∴∠A=30°,∴AB=2BC=6 cm.
①当∠EDB=90°时,如图1,∵
∵∠C=90°,∴∠EDB=∠C,
又∵∠B=∠B,∴△BDE∽△BCA,
∴BE=4cm,则AE=6-4=2(cm),在从 A到E 的过程中,t=2,满足题意,在从 B到E 的过程中,t=6+4=10,∵,∴t=10舍去.
②当∠BED=90°时,如图2,
∵∠DEB=∠C=90°,∠B=∠B,∴△BED∽△BCA,
∴BE=1cm,∴AE=5cm,
在从A到E 的过程中,t=5,满足题意,在从B到E的过程中,t=6+1=7,满足题意.综上所述,t=2或5或7.
12. D 解析:连接BD,
∵DF+BF≥BD,当 D,F,B 共线时取等号,∴线段 DF+BF 的值最小时,点 F 在 BD上的点F'处,此时点 E在点E'处,如图,
在矩形 ABCD中,AD=3,AB=4,则 BD=
由折叠性质得
4-AE',
在Rt△E'F'B 中,由勾股定理得
解得 即线段 DF+BF的值最小时,AE的长度为 .
13. 14.3 15. AC=BD且AC⊥BD 17.7
18.(40-x)(30+6x)=2100 19.12
21.解:(1)原式
(2)原式:
)
.
22.解:
这里
∵
(2)两边都除以2,得 移项,得
配方,得 即
开平方,得 即
(3)原方程可变形为( 0.
∴(y+2+2y+1)(y+2-2y-1)=0.∴3y+3=0,1-y=0,
∴y =-1,y =1.
23.解:(1)如图,△A'B'C'即为所求作;
(2)如图, 2
∵OA=4,OC=4,
∴四边形 AA'C'C 的周长
24.解:(1)∵方程. 有两个不相等的实数根,
∴[-(2k+1)] -4×1×(k +1)=4k-3>0.
(2)当k=2时,原方程为 设方程的两个根为m,n,
∴m+n=5, mn=5,
25.解:由题意,得AB⊥BD,CD⊥BD,
∴∠BEA + ∠BAE = 90°, ∠ECD +∠DEC=90°,∠ABE=∠EDC=90°,
∵∠MEN=90°,∴∠BEA+∠DEC=90°.∴∠BAE=∠DEC.
∴△ABE∽△EDC,
设AB=CD= xm,则 解得x=18(负值舍去).
经检验,x=18是原方程的解.
答:两栋建筑物的高度为18 m.
26.解:(1)设该市参加健身运动人数的年均增长率为x,
由题意,得32(1+x) =50,解得x =0.25=25%,x =-2.25(不符合题意,舍去),
答:该市参加健身运动人数的年均增长率为25%;
(2)∵1 600×100=160 000<240 000元,∴购买的这种健身器材的套数大于100套,设购买的这种健身器材的套数为m套,
由题 意,得 240 000,
整理,得 解得
当m=300 时,售价 40=800<1000(不符合题意,故舍去),
答:购买的这种健身器材的套数为200套.
27.解:(1)证明:∵四边形 ABCD是矩形,∴∠BAD=90°,∴∠ABE+∠AEB=90°,
∵∠ABE=∠DAF,∴∠DAF+∠AEB=90°,∴∠AOE=90°,∴AF⊥BE;
(2)延长AF交CD 于点G,
∵四边形ABCD为矩形,∴AB∥CD,∠BAD=∠ADG=90°,
∴△AFB∽△GFD,
∵∠BAD = ∠ADG = 90°, ∠ABE =∠DAF,
∴△ABE∽△DAG,
(3)设正方形 ABCD 的边长为a,则AB=AD=a,延长AF交CD于点G,
∵四边形ABCD 是正方形,∴∠BAD=∠ADG=90°,AB∥CD,
∴△AFB∽△GFD,
28.解:(1)证明:∵∠A=40°,∠B=60°,
∵∠A≠∠B≠∠ACB,∴△ABC不是等腰三角形.
∵CD平分∠ACB,
∴∠ACD=∠A=40°.∴AD=CD.∴△ACD为等腰三角形.
∵∠DCB=∠A=40°.∠CBD=∠ABC,∴△BCD∽△BAC.∴CD 是△ABC的完美分割线;
(2)∵△ACD 是以CD 为底边的等腰三角形,∴AD=AC=2,∴AB=AD+BD=2+BD.
∵CD 是△ABC 的完美分割线,∴△BCD∽△BAC.
解得 或 (不合题意,舍去),
∵△BCD∽△BAC,
(3)∵CD 是△ABC 的完美分割线,且△ACD为等腰三角形,
∴①当 AC=AD 时,∠ACD=∠ADC=
∵△BCD∽△BAC,∴∠BCD=∠A=48°,
②当AD=CD时,∠A=∠ACD=48°,
∵△BCD∽△BAC,∴∠BCD=∠A=48°,
③当CD=AC时,△ABC不存在.
故答案为:96°或114°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
