第九章 图形的相似 2 平行线分线段成比例(含答案)
文档属性
| 名称 | 第九章 图形的相似 2 平行线分线段成比例(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 418.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
2 平行线分线段成比例
轻松过关
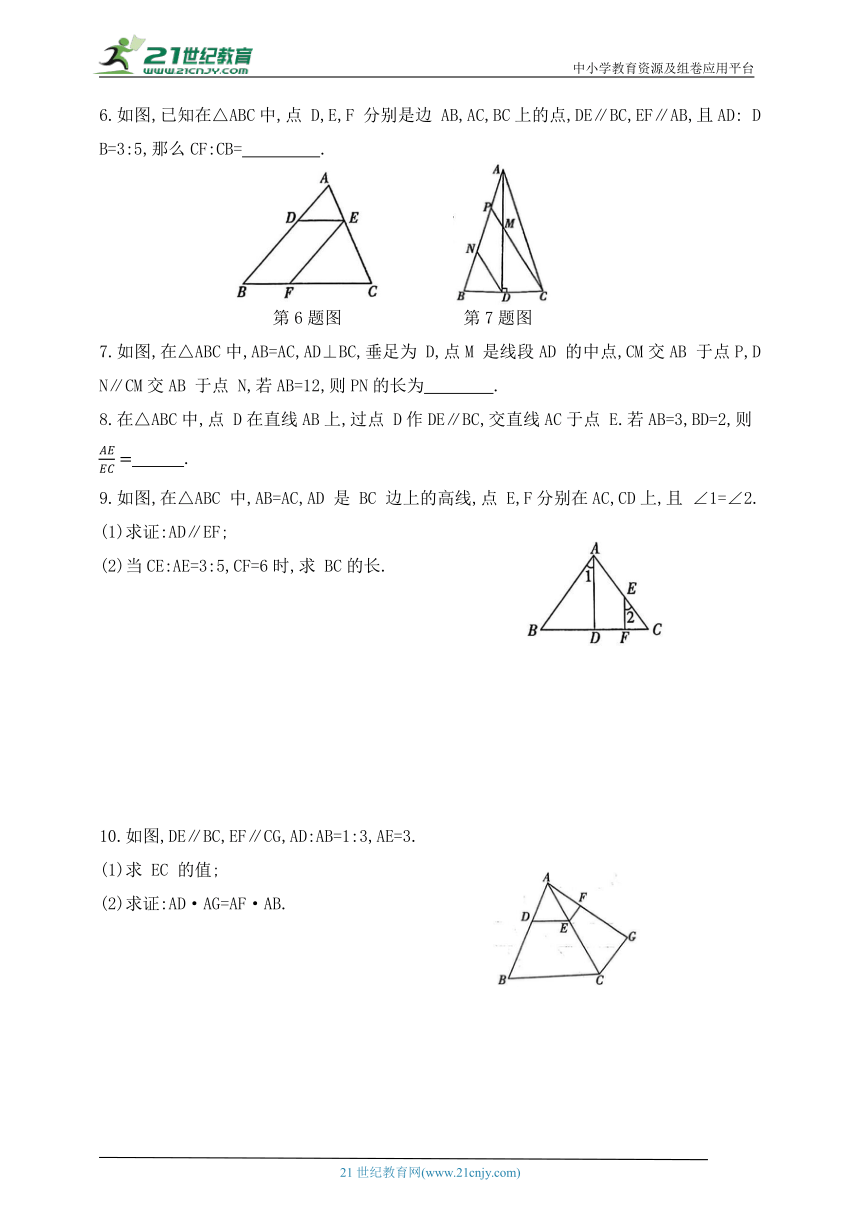
1.如图,已知 AD∥BE∥CF,若 AB=2BC,DF=12,则 EF的长为 ( )
A.2 B.4 C.6 D.8
第1题图 第2题图
2.如图所示,在△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
3.如图,在△ABC中,点 D 在边AB 上,过点 D作 DE∥BC,交 AC 于点 E.若AD=2,BD=3,则 的值是 ( )
A. B. C. D.
第3题图 第4题图
4.AD 是△ABC 的中线,E 是AD 上一点, BE 的延长线交AC 于F,则 的值为 .
5.如图,直线 AE,BF 交于点O,AB∥CD∥EF.若OA=1,AC=2,CE=4,则 的值为 .
6.如图,已知在△ABC中,点 D,E,F 分别是边 AB,AC,BC上的点,DE∥BC,EF∥AB,且AD: DB=3:5,那么CF:CB= .
第6题图 第7题图
7.如图,在△ABC中,AB=AC,AD⊥BC,垂足为 D,点M 是线段AD 的中点,CM交AB 于点P,DN∥CM交AB 于点 N,若AB=12,则PN的长为 .
8.在△ABC中,点 D在直线AB上,过点 D作DE∥BC,交直线AC于点 E.若AB=3,BD=2,则 .
9.如图,在△ABC 中,AB=AC,AD 是 BC 边上的高线,点 E,F分别在AC,CD上,且 ∠1=∠2.
(1)求证:AD∥EF;
(2)当CE:AE=3:5,CF=6时,求 BC的长.
10.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求 EC 的值;
(2)求证:AD·AG=AF·AB.
11.如图,已知AC∥FE∥BD,求证:
快乐拓展
12.如图,在△ABC 中,点 D 在 BC 上,F 是AD 的中点,连接 CF 并延长,交 AB 于点E,求证:
(2)已知CD:BD=3:2,求 的值.
13.阅读与计算:请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图 1,在△ABC中,AD平分∠BAC,则 下面是这个定理的部分证明过程.
证明:如图 2,过点 C 作 CE∥DA,交 BA的延长线于点 E……
任务:(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)如图3,在△ABC中,AD 是角平分线,AB=5cm ,AC=4 cm,BC=7 cm.求 BD的长.
参考答案
1. B 2. C 3. A
4. 5. 6.5:8 7.4
8. 或 解析:如图1,当点 D 在线段AB上时,AB=3,BD=2,则AD=AB-BD=3-2=1,
∵DE∥BC,
如图2,当点 D 在线段AB 的延长线上时,AB=3,BD=2,则AD=AB+BD=3+2=5,
∵DE∥BC,
9.解:(1)证明:∵AB=AC,AD是BC 边上的高线,∴BD=DC,∠1=∠CAD,
∵∠1=∠2,∴∠CAD=∠2,∴EF∥AD;
(2)∵EF∥AD,
∵CE:AE=3:5,CF=6,解得 FD=10,
∴CD=CF+DF=10+6=16,∴BC=2CD=32.
10.解:(1)∵DE∥BC,
解得AC=9,
∴EC=AC-AE=9-3=6;
(2)证明:∵DE∥BC,EF∥CG,
∴AD·AG=AF·AB.
11.证明:∵AC∥EF,
∵FE∥BD,
①+②,得 即
12.解:(1)作 DG∥CE,交AB于点G,如图,
∵DG∥CE,
∵F是AD 的中点,∴AF=DF,∴AE=EG,
(2)∵CD:BD=3:2,∴CD: BC=3:5,
13.解:(1)证明:如图2,过点C作CE∥DA,交BA 的延长线于点E,
∵CE∥DA,∴BD=BA,∠CAD=∠ACE,∠BAD =∠E,
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ACE=∠E,∴AE=AC,
(2)∵AD是角平分线,
∵AB=5cm,AC=4 cm,BC=7 cm,解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
2 平行线分线段成比例
轻松过关
1.如图,已知 AD∥BE∥CF,若 AB=2BC,DF=12,则 EF的长为 ( )
A.2 B.4 C.6 D.8
第1题图 第2题图
2.如图所示,在△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
3.如图,在△ABC中,点 D 在边AB 上,过点 D作 DE∥BC,交 AC 于点 E.若AD=2,BD=3,则 的值是 ( )
A. B. C. D.
第3题图 第4题图
4.AD 是△ABC 的中线,E 是AD 上一点, BE 的延长线交AC 于F,则 的值为 .
5.如图,直线 AE,BF 交于点O,AB∥CD∥EF.若OA=1,AC=2,CE=4,则 的值为 .
6.如图,已知在△ABC中,点 D,E,F 分别是边 AB,AC,BC上的点,DE∥BC,EF∥AB,且AD: DB=3:5,那么CF:CB= .
第6题图 第7题图
7.如图,在△ABC中,AB=AC,AD⊥BC,垂足为 D,点M 是线段AD 的中点,CM交AB 于点P,DN∥CM交AB 于点 N,若AB=12,则PN的长为 .
8.在△ABC中,点 D在直线AB上,过点 D作DE∥BC,交直线AC于点 E.若AB=3,BD=2,则 .
9.如图,在△ABC 中,AB=AC,AD 是 BC 边上的高线,点 E,F分别在AC,CD上,且 ∠1=∠2.
(1)求证:AD∥EF;
(2)当CE:AE=3:5,CF=6时,求 BC的长.
10.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求 EC 的值;
(2)求证:AD·AG=AF·AB.
11.如图,已知AC∥FE∥BD,求证:
快乐拓展
12.如图,在△ABC 中,点 D 在 BC 上,F 是AD 的中点,连接 CF 并延长,交 AB 于点E,求证:
(2)已知CD:BD=3:2,求 的值.
13.阅读与计算:请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理:如图 1,在△ABC中,AD平分∠BAC,则 下面是这个定理的部分证明过程.
证明:如图 2,过点 C 作 CE∥DA,交 BA的延长线于点 E……
任务:(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)如图3,在△ABC中,AD 是角平分线,AB=5cm ,AC=4 cm,BC=7 cm.求 BD的长.
参考答案
1. B 2. C 3. A
4. 5. 6.5:8 7.4
8. 或 解析:如图1,当点 D 在线段AB上时,AB=3,BD=2,则AD=AB-BD=3-2=1,
∵DE∥BC,
如图2,当点 D 在线段AB 的延长线上时,AB=3,BD=2,则AD=AB+BD=3+2=5,
∵DE∥BC,
9.解:(1)证明:∵AB=AC,AD是BC 边上的高线,∴BD=DC,∠1=∠CAD,
∵∠1=∠2,∴∠CAD=∠2,∴EF∥AD;
(2)∵EF∥AD,
∵CE:AE=3:5,CF=6,解得 FD=10,
∴CD=CF+DF=10+6=16,∴BC=2CD=32.
10.解:(1)∵DE∥BC,
解得AC=9,
∴EC=AC-AE=9-3=6;
(2)证明:∵DE∥BC,EF∥CG,
∴AD·AG=AF·AB.
11.证明:∵AC∥EF,
∵FE∥BD,
①+②,得 即
12.解:(1)作 DG∥CE,交AB于点G,如图,
∵DG∥CE,
∵F是AD 的中点,∴AF=DF,∴AE=EG,
(2)∵CD:BD=3:2,∴CD: BC=3:5,
13.解:(1)证明:如图2,过点C作CE∥DA,交BA 的延长线于点E,
∵CE∥DA,∴BD=BA,∠CAD=∠ACE,∠BAD =∠E,
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ACE=∠E,∴AE=AC,
(2)∵AD是角平分线,
∵AB=5cm,AC=4 cm,BC=7 cm,解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
