第九章 图形的相似 4 探索三角形相似的条件 第1课时 利用角的关系判定两个三角形相似(含答案)
文档属性
| 名称 | 第九章 图形的相似 4 探索三角形相似的条件 第1课时 利用角的关系判定两个三角形相似(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 443.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定两个三角形相似
轻松过关
1.下列各组图形中,不一定相似的是 ( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
2.如图,在矩形ABCD中,E,F 分别是 DC, BC 边上的点,且∠AEF=90°,则下列结论正确的是 ( )
A.△ABF∽△AEF B.△ABF∽△CEF C.△CEF∽△DAE D.△DAE∽△BAF
第2题图 第3题图
3.如图,在△ABC中,D,E分别是AB 和AC 上的点,DE∥BC,若 那么 ( )
A. B. C. D.
4.如图,AC,BD相交于点O,AB∥DC,M 是 AB 的中点, MN∥AC,交 BD 于点 N,若DO:OB=1: 2,AC=12,则 MN 的长为 ( )
A.2 B.4 C.6 D.8
第4题图 第5题图
5.如图,△ABC为等边三角形,点 D,E 分别在边 BC,AB 上,∠ADE=60°.若 BD=4DC,DE=2.4,则AD 的长为( )
A.1.8 B.2.4 C.3 D.3.2
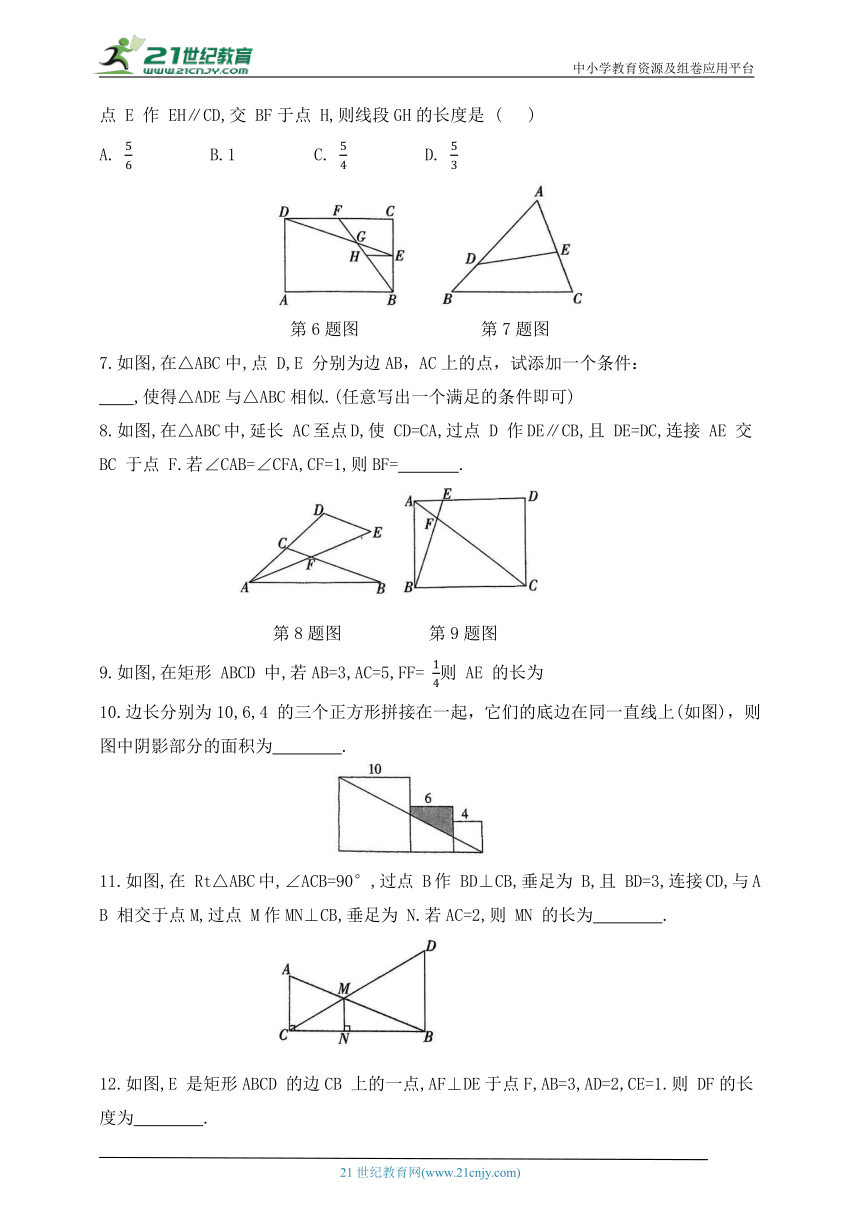
6.如图,在矩形 ABCD 中,AB=6,AD=4,点 E,F分别为 BC,CD的中点,BF,DE相交于点G,过点 E 作 EH∥CD,交 BF于点 H,则线段GH的长度是 ( )
A. B.1 C. D.
第6题图 第7题图
7.如图,在△ABC中,点 D,E 分别为边AB,AC上的点,试添加一个条件: ,使得△ADE与△ABC相似.(任意写出一个满足的条件即可)
8.如图,在△ABC中,延长 AC至点D,使 CD=CA,过点 D 作DE∥CB,且 DE=DC,连接 AE 交 BC 于点 F.若∠CAB=∠CFA,CF=1,则BF= .
第8题图 第9题图
9.如图,在矩形 ABCD 中,若AB=3,AC=5,FF= 则 AE 的长为
10.边长分别为10,6,4 的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
11.如图,在 Rt△ABC中,∠ACB=90°,过点 B作 BD⊥CB,垂足为 B,且 BD=3,连接CD,与AB 相交于点M,过点 M作MN⊥CB,垂足为 N.若AC=2,则 MN 的长为 .
12.如图,E 是矩形ABCD 的边CB 上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.则 DF的长度为 .
13.如图,在菱形 ABCD 中,∠ABC=60°,对角线 AC 与 BD 相交于点O,点 F 为 BC 的中点,连接 AF 与 BD 相交于点 E,连接CE 并延长交AB 于点G.
(1)证明:△BEF∽△BCO;
(2)证明:△BEG≌△AEG.
14.如图,在 ABCD中,点E是AD的中点,连接CE并延长交BA 的延长线于点F.
(1)求证:AF=AB;
(2)点 G 是线段AF 上一点,满足∠FCG=∠FCD,CG 交 AD 于点 H,若 AG=2,FG=6,求GH的长.
15.如图所示,在矩形 ABCD中,E为边CD 上一点,且AE⊥BD.
(1)求证:
(2)F为线段 AE 延长线上一点,且满足 求证:CE=AD.
快乐拓展
16.如图,直线 与x轴交于点A,与y轴交于点 B,在第一象限内找点 C,使△AOC与△AOB 相似,则共能找到的点 C的个数为 ( )
A.1 B.2 C.3 D.4
第16题图 第17题图
17.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点 P 在边 BC 上(不与点B,C重合),过点 P 作直线截△ABC,使截得的新三角形与原△ABC 相似,当截得新三角形与原△ABC相似的个数仅为3时,则 PC的取值范围为 .
参考答案
1. D 2. C 3. D 4. B 5. C 6. A
7.∠ADE=∠C(答案不唯一) 8. 3 9. 1 10. 15 11.
13.证明:(1)∵四边形 ABCD是菱形,∴AB=BC,AC⊥BD,
又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,
∵点 F为BC 的中点,∴AF⊥BC,∴∠BOC=∠BFE=90°,
又∵∠EBF=∠CBO,∴△BEF∽△BCO;
(2)∵BO⊥AC,AF⊥BC,∴CG⊥AB,∴∠BGE=∠AGE.
又∵AC=BC,∴BG=AG.
在△BEG和△AEG中,∴△BEG≌△AEG(SAS).
14.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AD∥BC,CD∥AB,∴∠D=∠FAD,∠DCE=∠F,
∵E是AD的中点,∴DE=AE,∴△CDE≌△FAE(AAS),∴CE=EF,
∵AE∥BC,∴AF=AB;
(2)∵AG=2,FG=6,∴AF=FG+AG=6+2=8,∴AB=AF=8,
∵四边形ABCD是平行四边形,∴CD=AB=8,
∵∠DCE=∠F,∠FCG=∠FCD,∴∠F=∠FCG,∴CG=FG=6,
∵CD∥AF,∴△DCH∽△AGH,即 ∴GH=1.2.
15.证明:(1)∵四边形 ABCD 是矩形,
∴∠BAD=90°,∠ADE=90°,AB=DC,∴∠ABD+∠ADB=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
∵AB=DC,∴AD =DE·DC;
(2)连接AC,交 BD于点O,
∵四边形ABCD 是矩形,∴∠ADE=90°,∴∠DAE+∠AED=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠ADB=∠AED,
∵∠FEC=∠AED,∴∠ADO=∠FEC,
∵四边形 ABCD 是矩形,
∴OA=OD=EF=CF,∴∠ADO=∠OAD,∠FEC=∠FCE,
∵∠ADO=∠FEC,∴∠ADO=∠OAD=∠FEC=∠FCE,
在△ODA 和△FEC中,∴△ODA≌△FEC(AAS),∴CE=AD.
16. D 解析:∵点C在第一象限,∴当点C为直角顶点时,有两种情形,如图点 C ,C ,当点 A 为直角顶点时,也有两种情形,如图点 C ,C ,共有4种情形.
解析:如图,过点 A作∠CAP=∠B,
则△PCA∽△ACB,
∵AC=3,BC=4,解得
∴当截得新三角形与原△ABC 相似的个数仅为31时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定两个三角形相似
轻松过关
1.下列各组图形中,不一定相似的是 ( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
2.如图,在矩形ABCD中,E,F 分别是 DC, BC 边上的点,且∠AEF=90°,则下列结论正确的是 ( )
A.△ABF∽△AEF B.△ABF∽△CEF C.△CEF∽△DAE D.△DAE∽△BAF
第2题图 第3题图
3.如图,在△ABC中,D,E分别是AB 和AC 上的点,DE∥BC,若 那么 ( )
A. B. C. D.
4.如图,AC,BD相交于点O,AB∥DC,M 是 AB 的中点, MN∥AC,交 BD 于点 N,若DO:OB=1: 2,AC=12,则 MN 的长为 ( )
A.2 B.4 C.6 D.8
第4题图 第5题图
5.如图,△ABC为等边三角形,点 D,E 分别在边 BC,AB 上,∠ADE=60°.若 BD=4DC,DE=2.4,则AD 的长为( )
A.1.8 B.2.4 C.3 D.3.2
6.如图,在矩形 ABCD 中,AB=6,AD=4,点 E,F分别为 BC,CD的中点,BF,DE相交于点G,过点 E 作 EH∥CD,交 BF于点 H,则线段GH的长度是 ( )
A. B.1 C. D.
第6题图 第7题图
7.如图,在△ABC中,点 D,E 分别为边AB,AC上的点,试添加一个条件: ,使得△ADE与△ABC相似.(任意写出一个满足的条件即可)
8.如图,在△ABC中,延长 AC至点D,使 CD=CA,过点 D 作DE∥CB,且 DE=DC,连接 AE 交 BC 于点 F.若∠CAB=∠CFA,CF=1,则BF= .
第8题图 第9题图
9.如图,在矩形 ABCD 中,若AB=3,AC=5,FF= 则 AE 的长为
10.边长分别为10,6,4 的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
11.如图,在 Rt△ABC中,∠ACB=90°,过点 B作 BD⊥CB,垂足为 B,且 BD=3,连接CD,与AB 相交于点M,过点 M作MN⊥CB,垂足为 N.若AC=2,则 MN 的长为 .
12.如图,E 是矩形ABCD 的边CB 上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.则 DF的长度为 .
13.如图,在菱形 ABCD 中,∠ABC=60°,对角线 AC 与 BD 相交于点O,点 F 为 BC 的中点,连接 AF 与 BD 相交于点 E,连接CE 并延长交AB 于点G.
(1)证明:△BEF∽△BCO;
(2)证明:△BEG≌△AEG.
14.如图,在 ABCD中,点E是AD的中点,连接CE并延长交BA 的延长线于点F.
(1)求证:AF=AB;
(2)点 G 是线段AF 上一点,满足∠FCG=∠FCD,CG 交 AD 于点 H,若 AG=2,FG=6,求GH的长.
15.如图所示,在矩形 ABCD中,E为边CD 上一点,且AE⊥BD.
(1)求证:
(2)F为线段 AE 延长线上一点,且满足 求证:CE=AD.
快乐拓展
16.如图,直线 与x轴交于点A,与y轴交于点 B,在第一象限内找点 C,使△AOC与△AOB 相似,则共能找到的点 C的个数为 ( )
A.1 B.2 C.3 D.4
第16题图 第17题图
17.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点 P 在边 BC 上(不与点B,C重合),过点 P 作直线截△ABC,使截得的新三角形与原△ABC 相似,当截得新三角形与原△ABC相似的个数仅为3时,则 PC的取值范围为 .
参考答案
1. D 2. C 3. D 4. B 5. C 6. A
7.∠ADE=∠C(答案不唯一) 8. 3 9. 1 10. 15 11.
13.证明:(1)∵四边形 ABCD是菱形,∴AB=BC,AC⊥BD,
又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,
∵点 F为BC 的中点,∴AF⊥BC,∴∠BOC=∠BFE=90°,
又∵∠EBF=∠CBO,∴△BEF∽△BCO;
(2)∵BO⊥AC,AF⊥BC,∴CG⊥AB,∴∠BGE=∠AGE.
又∵AC=BC,∴BG=AG.
在△BEG和△AEG中,∴△BEG≌△AEG(SAS).
14.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AD∥BC,CD∥AB,∴∠D=∠FAD,∠DCE=∠F,
∵E是AD的中点,∴DE=AE,∴△CDE≌△FAE(AAS),∴CE=EF,
∵AE∥BC,∴AF=AB;
(2)∵AG=2,FG=6,∴AF=FG+AG=6+2=8,∴AB=AF=8,
∵四边形ABCD是平行四边形,∴CD=AB=8,
∵∠DCE=∠F,∠FCG=∠FCD,∴∠F=∠FCG,∴CG=FG=6,
∵CD∥AF,∴△DCH∽△AGH,即 ∴GH=1.2.
15.证明:(1)∵四边形 ABCD 是矩形,
∴∠BAD=90°,∠ADE=90°,AB=DC,∴∠ABD+∠ADB=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
∵AB=DC,∴AD =DE·DC;
(2)连接AC,交 BD于点O,
∵四边形ABCD 是矩形,∴∠ADE=90°,∴∠DAE+∠AED=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠ADB=∠AED,
∵∠FEC=∠AED,∴∠ADO=∠FEC,
∵四边形 ABCD 是矩形,
∴OA=OD=EF=CF,∴∠ADO=∠OAD,∠FEC=∠FCE,
∵∠ADO=∠FEC,∴∠ADO=∠OAD=∠FEC=∠FCE,
在△ODA 和△FEC中,∴△ODA≌△FEC(AAS),∴CE=AD.
16. D 解析:∵点C在第一象限,∴当点C为直角顶点时,有两种情形,如图点 C ,C ,当点 A 为直角顶点时,也有两种情形,如图点 C ,C ,共有4种情形.
解析:如图,过点 A作∠CAP=∠B,
则△PCA∽△ACB,
∵AC=3,BC=4,解得
∴当截得新三角形与原△ABC 相似的个数仅为31时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
