第九章 图形的相似 4 探索三角形相似的条件 第2课时 利用边角的关系判定两个三角形相似(含答案)
文档属性
| 名称 | 第九章 图形的相似 4 探索三角形相似的条件 第2课时 利用边角的关系判定两个三角形相似(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 501.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-15 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角的关系判定两个三角形相似
轻松过关
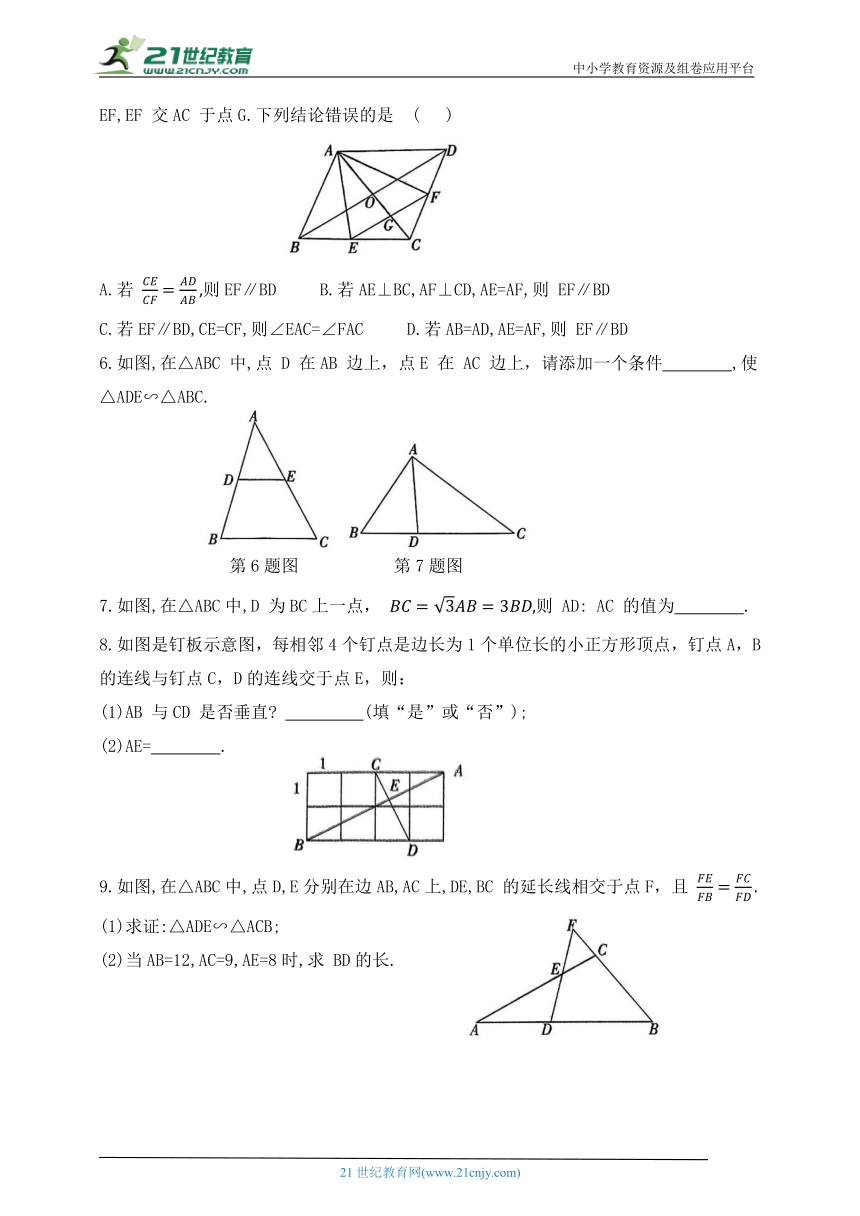
1.如图,在△ABC 中,∠A=76°,AB=8,AC=6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
2.如图,添加以下哪个条件,仍不能直接证明△ABC与△ADE相似( )
A.∠B=∠ADE B.∠C=∠AED
第2题图 第3题图
3.如图,在正三角形ABC中,点 D,E 分别在 AC,AB 上,且 那么有△AED∽( )
A.△BED B.△ABD C.△CBD D.△ABC
4.如图,点 E 在矩形ABCD 的AB 边上,将△ADE沿 DE 翻折,点 A 恰好落在 BC边上的点 F处,若CD=3BF,BE=4,则AD的长为 ( )
A.9 B.12 C.15 D.18
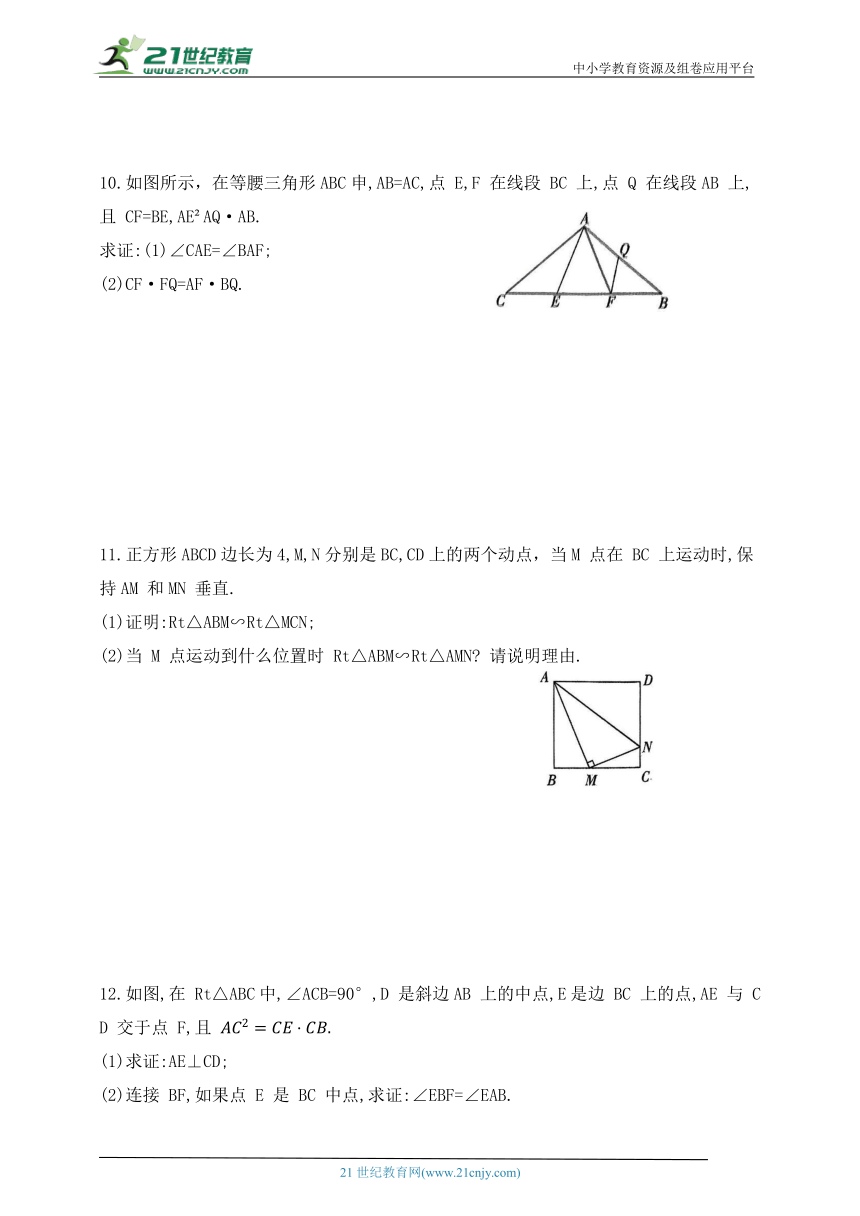
5.如图,在 ABCD中,对角线AC,BD 交于点O,点 E 在 BC 上,点 F 在CD 上,连接AE,AF,EF,EF 交AC 于点G.下列结论错误的是 ( )
A.若 则EF∥BD B.若AE⊥BC,AF⊥CD,AE=AF,则 EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC D.若AB=AD,AE=AF,则 EF∥BD
6.如图,在△ABC 中,点 D 在AB 边上,点E 在 AC 边上,请添加一个条件 ,使△ADE∽△ABC.
第6题图 第7题图
7.如图,在△ABC中,D 为BC上一点, 则 AD: AC 的值为 .
8.如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则:
(1)AB 与CD 是否垂直 (填“是”或“否”);
(2)AE= .
9.如图,在△ABC中,点D,E分别在边AB,AC上,DE,BC 的延长线相交于点F,且
(1)求证:△ADE∽△ACB;
(2)当AB=12,AC=9,AE=8时,求 BD的长.
10.如图所示,在等腰三角形ABC申,AB=AC,点 E,F 在线段 BC 上,点 Q 在线段AB 上,且 CF=BE,AE AQ·AB.
求证:(1)∠CAE=∠BAF;
(2)CF·FQ=AF·BQ.
11.正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M 点在 BC 上运动时,保持AM 和MN 垂直.
(1)证明:Rt△ABM∽Rt△MCN;
(2)当 M 点运动到什么位置时 Rt△ABM∽Rt△AMN 请说明理由.
12.如图,在 Rt△ABC中,∠ACB=90°,D 是斜边AB 上的中点,E是边 BC 上的点,AE 与 CD 交于点 F,且
(1)求证:AE⊥CD;
(2)连接 BF,如果点 E 是 BC 中点,求证:∠EBF=∠EAB.
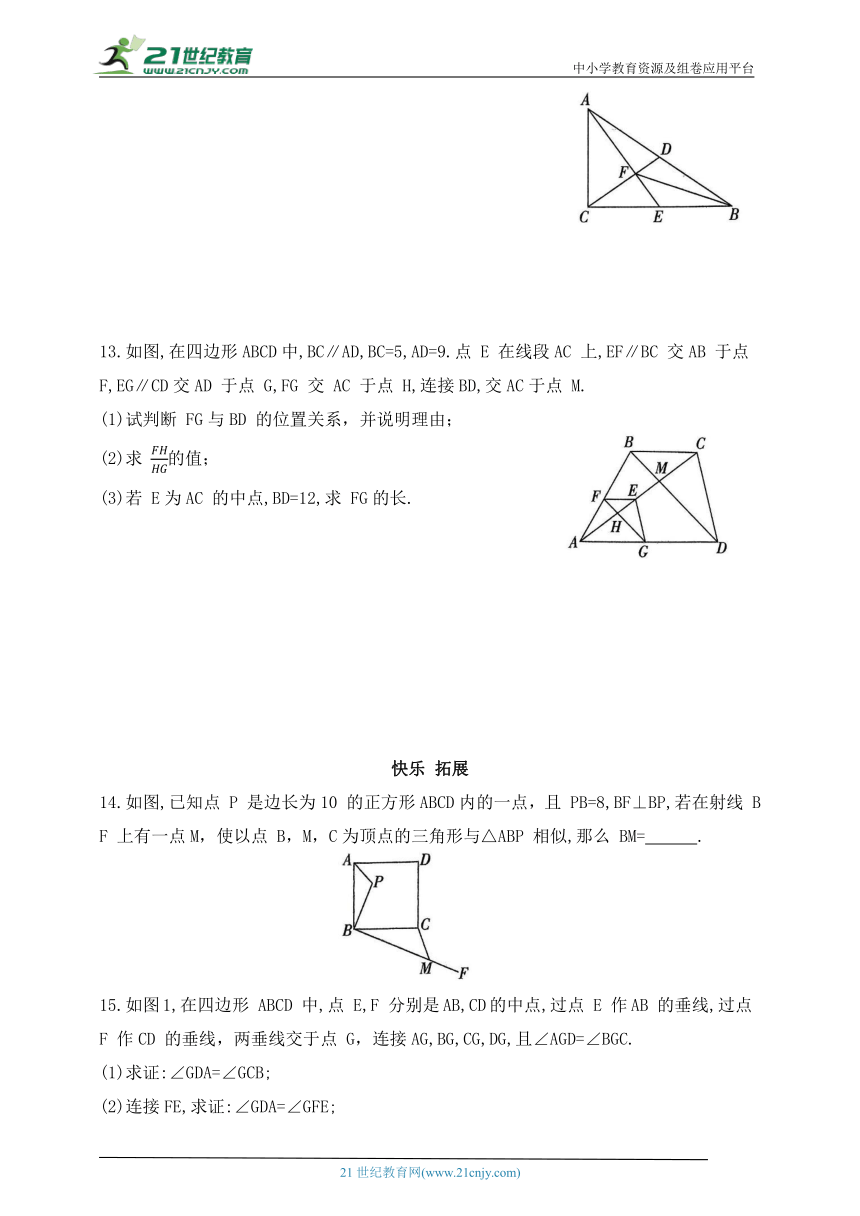
13.如图,在四边形ABCD中,BC∥AD,BC=5,AD=9.点 E 在线段AC 上,EF∥BC 交AB 于点 F,EG∥CD交AD 于点 G,FG 交 AC 于点 H,连接BD,交AC于点 M.
(1)试判断 FG与BD 的位置关系,并说明理由;
(2)求 的值;
(3)若 E为AC 的中点,BD=12,求 FG的长.
快乐 拓展
14.如图,已知点 P 是边长为10 的正方形ABCD内的一点,且 PB=8,BF⊥BP,若在射线 BF 上有一点M,使以点 B,M,C为顶点的三角形与△ABP 相似,那么 BM= .
15.如图1,在四边形 ABCD 中,点 E,F 分别是AB,CD的中点,过点 E 作AB 的垂线,过点 F 作CD 的垂线,两垂线交于点 G,连接AG,BG,CG,DG,且∠AGD=∠BGC.
(1)求证:∠GDA=∠GCB;
(2)连接FE,求证:∠GDA=∠GFE;
(3)如图2,若AD,BC所在直线互相垂直,试判断 是否为定值,若为定值请求出;若不存在定值请说明理由.
参考答案
1. C 2. D 3. C 4. C 5. D
6.∠ADE=∠B(或∠AED=∠C或 8.(1)是
9.解:(1)证明: 且∠EFC=∠BFD,∴△FEC∽△FBD,∴∠FEC=∠B,
又∵∠AED=∠FEC,∴∠AED=∠B,
又∵∠EAD=∠BAC,∴△ADE∽△ACB;
(2)∵△ADE∽△ACB,即
∴AD=6,∴DB=AB-AD=12-6=6.
10.证明:(1)∵AB=AC,∴∠B=∠C,
∵CF=BE,∴CF-EF=BE-EF,即CE=BF,
在△ACE和△ABF中,∴△ACE≌△ABF(SAS),∴∠CAE=∠BAF;
(2)∵△ACE≌△ABF,∴AE=AF,∠CAE=∠BAF,
∵AE =AQ·AB,AC=AB,∴△ACE∽△AFQ,
∴∠AEC=∠AQF,∴∠AEF=∠BQF,
∵AE=AF,∴∠AEF=∠AFE,∴∠BQF=∠AFE,
∵∠B=∠C,∴△CAF∽△BFQ,即 CF·FQ=AF·BQ.
11.解:(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°,
∵AM⊥MN,∴∠AMN=90°,∴∠AMB+∠NMC=90°,
又∵∠AMB+∠MAB=90°,∴∠MAB=∠NMC,∴Rt△ABM∽Rt△MCN;
(2)当M 点 运 动 到 BC 中 点 位 置时,Rt△ABM∽Rt△AMN.
理由如下:
∵四边形ABCD为正方形,∴AB=BC=4,BM=MC=2,
∵Rt△ABM∽Rt△MCN,
∵BM=MC,
又∵∠ABM=∠AMN=90°,∴Rt△ABM∽Rt△AMN.
12.证明:(1)∵AC =CE·CB,
又∵∠ACB=∠ECA=90°,∴△ACB∽△ECA,∴∠ABC=∠EAC.
∵点 D 是AB 的中点,∴CD=AD,∴∠ACD=∠CAD,
∵∠CAD+∠ABC=90°,∴∠ACD+∠EAC=90°,∴∠AFC=90°,∴AE⊥CD;
(2)∵AE⊥CD,∴∠EFC=90°,∴∠ACE=∠EFC,
又∵∠AEC=∠CEF,∴△ECF∽△EAC,
∵点E是BC 的中点,∴CE=BE.
∵∠BEF=∠AEB.∴△BEF∽△AEB.∴∠EBF=∠EAB.
13.解:(1)FG∥BD.理由如下:
∵EF∥BC,
∵EG∥CD,
∵∠FAG=∠BAD,∴△AFG∽△ABD,∴∠AFG=∠ABD,∴FG∥BD;
(2)∵BC∥AD,∴△BCM∽△DAM,
由(1),得 FG∥BD,即 FH∥BM,∴△AFH∽△ABM,
同理,得
(3)∵EF∥BC,
∵E为AC 的中点,即点 F 是AB 的中点,
∥即点G是AD的中点,
∴FG是△ABD的中位线,
14.8或12.5
15.解:(1)证明:∵点 E 是AB 的中点,GE⊥AB,∴GE是AB 的垂直平分线,
∴GA=GB,同理,得GD=GC,
在△AGD和△BGC中,∴△AGD≌△BGC(SAS),
∴∠GDA=∠GCB;
(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC,
∴△AGB∽△DGC,∴∠GAE=∠GDC,
又∵∠GEA=∠GFD=90°,∴△GAE∽△GDF,
∴∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF,∴∠GDA=∠GFE;
(3)延长AD交GB 于点M,交 BC的延长线于点 H,如图,
则AH⊥BH,
∵△AGD≌△BGC,∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,∴∠AGB=∠AHB=90°,
∵△AGD∽△EGF,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角的关系判定两个三角形相似
轻松过关
1.如图,在△ABC 中,∠A=76°,AB=8,AC=6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
2.如图,添加以下哪个条件,仍不能直接证明△ABC与△ADE相似( )
A.∠B=∠ADE B.∠C=∠AED
第2题图 第3题图
3.如图,在正三角形ABC中,点 D,E 分别在 AC,AB 上,且 那么有△AED∽( )
A.△BED B.△ABD C.△CBD D.△ABC
4.如图,点 E 在矩形ABCD 的AB 边上,将△ADE沿 DE 翻折,点 A 恰好落在 BC边上的点 F处,若CD=3BF,BE=4,则AD的长为 ( )
A.9 B.12 C.15 D.18
5.如图,在 ABCD中,对角线AC,BD 交于点O,点 E 在 BC 上,点 F 在CD 上,连接AE,AF,EF,EF 交AC 于点G.下列结论错误的是 ( )
A.若 则EF∥BD B.若AE⊥BC,AF⊥CD,AE=AF,则 EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC D.若AB=AD,AE=AF,则 EF∥BD
6.如图,在△ABC 中,点 D 在AB 边上,点E 在 AC 边上,请添加一个条件 ,使△ADE∽△ABC.
第6题图 第7题图
7.如图,在△ABC中,D 为BC上一点, 则 AD: AC 的值为 .
8.如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则:
(1)AB 与CD 是否垂直 (填“是”或“否”);
(2)AE= .
9.如图,在△ABC中,点D,E分别在边AB,AC上,DE,BC 的延长线相交于点F,且
(1)求证:△ADE∽△ACB;
(2)当AB=12,AC=9,AE=8时,求 BD的长.
10.如图所示,在等腰三角形ABC申,AB=AC,点 E,F 在线段 BC 上,点 Q 在线段AB 上,且 CF=BE,AE AQ·AB.
求证:(1)∠CAE=∠BAF;
(2)CF·FQ=AF·BQ.
11.正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M 点在 BC 上运动时,保持AM 和MN 垂直.
(1)证明:Rt△ABM∽Rt△MCN;
(2)当 M 点运动到什么位置时 Rt△ABM∽Rt△AMN 请说明理由.
12.如图,在 Rt△ABC中,∠ACB=90°,D 是斜边AB 上的中点,E是边 BC 上的点,AE 与 CD 交于点 F,且
(1)求证:AE⊥CD;
(2)连接 BF,如果点 E 是 BC 中点,求证:∠EBF=∠EAB.
13.如图,在四边形ABCD中,BC∥AD,BC=5,AD=9.点 E 在线段AC 上,EF∥BC 交AB 于点 F,EG∥CD交AD 于点 G,FG 交 AC 于点 H,连接BD,交AC于点 M.
(1)试判断 FG与BD 的位置关系,并说明理由;
(2)求 的值;
(3)若 E为AC 的中点,BD=12,求 FG的长.
快乐 拓展
14.如图,已知点 P 是边长为10 的正方形ABCD内的一点,且 PB=8,BF⊥BP,若在射线 BF 上有一点M,使以点 B,M,C为顶点的三角形与△ABP 相似,那么 BM= .
15.如图1,在四边形 ABCD 中,点 E,F 分别是AB,CD的中点,过点 E 作AB 的垂线,过点 F 作CD 的垂线,两垂线交于点 G,连接AG,BG,CG,DG,且∠AGD=∠BGC.
(1)求证:∠GDA=∠GCB;
(2)连接FE,求证:∠GDA=∠GFE;
(3)如图2,若AD,BC所在直线互相垂直,试判断 是否为定值,若为定值请求出;若不存在定值请说明理由.
参考答案
1. C 2. D 3. C 4. C 5. D
6.∠ADE=∠B(或∠AED=∠C或 8.(1)是
9.解:(1)证明: 且∠EFC=∠BFD,∴△FEC∽△FBD,∴∠FEC=∠B,
又∵∠AED=∠FEC,∴∠AED=∠B,
又∵∠EAD=∠BAC,∴△ADE∽△ACB;
(2)∵△ADE∽△ACB,即
∴AD=6,∴DB=AB-AD=12-6=6.
10.证明:(1)∵AB=AC,∴∠B=∠C,
∵CF=BE,∴CF-EF=BE-EF,即CE=BF,
在△ACE和△ABF中,∴△ACE≌△ABF(SAS),∴∠CAE=∠BAF;
(2)∵△ACE≌△ABF,∴AE=AF,∠CAE=∠BAF,
∵AE =AQ·AB,AC=AB,∴△ACE∽△AFQ,
∴∠AEC=∠AQF,∴∠AEF=∠BQF,
∵AE=AF,∴∠AEF=∠AFE,∴∠BQF=∠AFE,
∵∠B=∠C,∴△CAF∽△BFQ,即 CF·FQ=AF·BQ.
11.解:(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°,
∵AM⊥MN,∴∠AMN=90°,∴∠AMB+∠NMC=90°,
又∵∠AMB+∠MAB=90°,∴∠MAB=∠NMC,∴Rt△ABM∽Rt△MCN;
(2)当M 点 运 动 到 BC 中 点 位 置时,Rt△ABM∽Rt△AMN.
理由如下:
∵四边形ABCD为正方形,∴AB=BC=4,BM=MC=2,
∵Rt△ABM∽Rt△MCN,
∵BM=MC,
又∵∠ABM=∠AMN=90°,∴Rt△ABM∽Rt△AMN.
12.证明:(1)∵AC =CE·CB,
又∵∠ACB=∠ECA=90°,∴△ACB∽△ECA,∴∠ABC=∠EAC.
∵点 D 是AB 的中点,∴CD=AD,∴∠ACD=∠CAD,
∵∠CAD+∠ABC=90°,∴∠ACD+∠EAC=90°,∴∠AFC=90°,∴AE⊥CD;
(2)∵AE⊥CD,∴∠EFC=90°,∴∠ACE=∠EFC,
又∵∠AEC=∠CEF,∴△ECF∽△EAC,
∵点E是BC 的中点,∴CE=BE.
∵∠BEF=∠AEB.∴△BEF∽△AEB.∴∠EBF=∠EAB.
13.解:(1)FG∥BD.理由如下:
∵EF∥BC,
∵EG∥CD,
∵∠FAG=∠BAD,∴△AFG∽△ABD,∴∠AFG=∠ABD,∴FG∥BD;
(2)∵BC∥AD,∴△BCM∽△DAM,
由(1),得 FG∥BD,即 FH∥BM,∴△AFH∽△ABM,
同理,得
(3)∵EF∥BC,
∵E为AC 的中点,即点 F 是AB 的中点,
∥即点G是AD的中点,
∴FG是△ABD的中位线,
14.8或12.5
15.解:(1)证明:∵点 E 是AB 的中点,GE⊥AB,∴GE是AB 的垂直平分线,
∴GA=GB,同理,得GD=GC,
在△AGD和△BGC中,∴△AGD≌△BGC(SAS),
∴∠GDA=∠GCB;
(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC,
∴△AGB∽△DGC,∴∠GAE=∠GDC,
又∵∠GEA=∠GFD=90°,∴△GAE∽△GDF,
∴∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF,∴∠GDA=∠GFE;
(3)延长AD交GB 于点M,交 BC的延长线于点 H,如图,
则AH⊥BH,
∵△AGD≌△BGC,∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,∴∠AGB=∠AHB=90°,
∵△AGD∽△EGF,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
